| Autor |
Nachricht |
Platonische Mathematik
Gast
|
 Platonische Mathematik Verfasst am: 24. März 2017 11:09 Titel: Mathematik im platonischen Reich unabhängig vom Universum |
 |
|
|
Ich stelle mir die Frage schon seit langem aber in der letzten Zeit wieder vermehrt. Ich habe auch versucht ein paar Publikation dazu zu lesen, ein paar interessante Wissenschaftler oder Mathematiker zu hören, komme aber selbst zu keiner definitiven Entscheidung oder Lösung. Existiert die Mathematik unabhängig vom Universum in einem immateriellen platonischen reich? Das ist, was mich wirklich beschäftigt momentan. Ich meine, wenn ich mir folgenden Hinweis oder Beleg anschaue. Komplexe Zahlen bzw die imaginäre Einheit oder zahl wurde erfunden, weil es vorher keiner Wurzel von -1 gab. Man legte also fest, es gibt sie und diese ist die Wurzel von -1. Das Quadrat dieser Zahl ergibt eine negative Zahl, nämlich -1. Was aber als Erfindung gedacht war, entpuppte sich meiner Ansicht nach als Teil der fundamentalen platonischen mathematischen Realität. Dann komplexe Zahlen und die imaginäre Zahl oder Einheit findet extrem häufiger Anwendung in der Quantenmechanik. Und diese ist grundlegend Struktur des Universums. Deshalb die Frage an die Community. Wie haltet ihr es mit dieser Meinung oder Ansicht. Seid ihr Platoniker oder Formalisten? Und warum seid ihr das? Warum glaubt ihr, dass das Universum mathematisch ist oder warum glaubt ihr ist die Mathematik ewig und zeitlos gültig? |
|
 |
Platonische Mathematik
Gast
|
| Platonische Mathematik Verfasst am: 24. März 2017 11:12 Titel: |
|
|
|
Ich habe noch folgende wichtige Überlegung. Was haltet ihr davon? Wenn ich an einer Zahl denke oder in eine Gleichung, nämlich 2 + 2 = 4. Dann fängt diese doch nicht erst an zu existieren, wenn ich oder der vielleicht der erste Mensch daran denke. Diese Gleichung hat doch den ontologischen Zustand, dass sie zeitlos ist und immer existiert und korrekt ist. Wenn es ein intelligentes Wesen zur Zeit der Dinosaurier gegeben hätte, wäre die Gleichung dort richtig gewesen. Was ist von diesem Gedanken zu halten? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 24. März 2017 17:42 Titel: |
|
|
Zur Sicherheit: du sprichst über reine Mathematik, d.h. du verknüpfst nicht die platonistische Existenzweise der Idee "i" der imaginären Einheit mit der Existenz von elektrischer Spannung und Strom, die du mit der Hilfe von "i" beschreibst.
Ich selbst habe für mich eine eher platonistische Sicht, und zwar sicher in der Physik als auch eher in der Mathematik. Ich halte wenig von konstruktivistischen / intuitionistischen Ansätzen; das sind für mich eher Ideen aus Psychologie und Sozialwissensachften, die dort ihre Berechtigungen haben mögen, die in der Naturwissenschaften jedoch überflüssig sind und in der Mathematik m.M.n. nicht "passen".
In vielen Diskussionen empfehle ich eher eine minimalistische formale Herangehensweise, einfach weil das Lernen von Mathematik und Physik schon schwierig genug ist, selbst wenn man philosophische Aspekte ausklammert. Viele populärwissenschaftliche Bücher sind da unsauber und erwecken den Eindruck, die Physiker wüssten, was "ist" bzw. "real existiert"; das ist natürlich falsch: die Physiker wissen lediglich, ob ein mathematisches Modell funktioniert; ob es im platonistischen Sinn selbst als Idee existiert oder die Realität true abbildet ist Glaubensache. In der Mathematik verhält es sich ähnlich: wer keine Differentialgleichung lösen kann, muss auch (noch) nicht darüber nachdenken, ob und ab wann die Funktion existiert, die die Differentialgleichung löst. Dass ich dazu eine platonistische Haltung einnehme versuche ich aus den Diskussione eher herauszuhalten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Platonische Mathematik
Gast
|
| Platonische Mathematik Verfasst am: 24. März 2017 17:57 Titel: |
|
|
|
Mit imaginärer Einheit bzw Zahl meine ich einfach die Wurzel aus -1. Dabei rede ich von der reinen Mathematik, wie du sagst. Nicht mit einer Verknüpfung zur Physik. Wenn du sagst, dass du ein platonischen Standpunkt oder eine platonische Sichtweise einnimmst, dann muss es doch gute Gründe dafür geben, zumindest für dich. Könntest du mir sagen, welche das sind? Ich meine, das mit der imaginären Einheit ist doch schon mal ein Grund, würde ich sagen. Und dass die Gleichung 2 + 2 = 4 nicht erst jetzt gerade in die Existenz getreten ist, klingt doch auch plausibel. Wenn es keine Menschen gäbe und keine intelligenten Geschöpfe im Universum, das heißt keine Struktur eines Gehirns, und es würden drei Steine zu zwei Stein fallen oder rollen, dann sind es doch fünf Steine. Die Mathematik existiert unabhängig von uns. Was sind denn gute Gründe für eine platonische Sicht auf die Mathematik? Und was spricht dagegen? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 25. März 2017 09:11 Titel: |
|
|
| Platonische Mathematik hat Folgendes geschrieben: | Wenn du sagst, dass du ein platonischen Standpunkt oder eine platonische Sichtweise einnimmst, dann muss es doch gute Gründe dafür geben, zumindest für dich. Könntest du mir sagen, welche das sind?
...
Die Mathematik existiert unabhängig von uns. Was sind denn gute Gründe für eine platonische Sicht auf die Mathematik? Und was spricht dagegen? |
Es ist eine Glaubenssache.
Wenn ein Künstler ein Kunstwerk schafft, oder wenn eine neue Kunstrichtung entsteht, dann ist der Künstler (sind die Künstler) davon überzeugt, etwas gänzlich Neues zu schaffen, was es vorher so noch nicht gegeben hat.
Wenn Mathematiker eine neue mathematische Struktur entdecken, dann fühlt es sich für sie so an, als ob sie sie entdecken, nicht erschaffen. Bsp. Primzahlen und Primzahlzwillinge: die Entdeckung einer neuen großen Primzahl empfinden die Mathematiker als Entdeckung von etwas bereits existierendem. Und sollte es tatsächlich einen größten Primzahlzwilling geben - was wir heute nicht wissen - dann würde er irgendwie heute schon existieren, nicht erst von uns geschaffen werden; seine Existenz - oder nicht-Existenz - ist mit der Definition der natürlichen Zahlen bereits gegeben. |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 25. März 2017 15:47 Titel: Re: Mathematik im platonischen Reich unabhängig vom Universu |
|
|
| Platonische Mathematik hat Folgendes geschrieben: | | Warum glaubt ihr, dass das Universum mathematisch ist oder warum glaubt ihr ist die Mathematik ewig und zeitlos gültig? |
Ich denke, Theologie, Mathematik und weitere Hilfskonstrukte dienen einem kleinen Teil der Menschheit als "Gehhilfe", mit ihren Gedanken einen Schritt in die Ferne zu tun.
Die Mathematik kann nicht ewig sein, weil sie an Intelligenz gebunden ist. Wo war die Mathematik vor Erschaffung / Erscheinung des Menschen?
Wo wird sie sein nach Aussterben der Menschheit? |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 25. März 2017 15:56 Titel: |
|
|
| Platonische Mathematik hat Folgendes geschrieben: | | 2 + 2 = 4. .. Diese Gleichung hat doch den ontologischen Zustand, dass sie zeitlos ist und immer existiert und korrekt ist. Wenn es ein intelligentes Wesen zur Zeit der Dinosaurier gegeben hätte, wäre die Gleichung dort richtig gewesen. Was ist von diesem Gedanken zu halten? |
Ich zweifle. Du addierst ein grafisches Symbol (2) zu einem anderen Symbol (nochmals 2) und bekommst ein drittes grafisches Symbol.
Diese Symbole gab es früher nicht. Wenn du weisst, dass die Römer II und II zusammenzählten, weisst du dann auch, wie das Ergebnis aussehen muss? IIII, ++ oder IV oder noch anders? Die richtige Antwort IV ist für mich unlogisch, weil man ein Streichholz übrig behält.
Und immer wieder falle ich darauf herein, dass ein Urlaub vom 2.Mai bis zum 5.Mai 3 Tage dauert. Falsch. Mit den arabischen Zahlen wurde uns auch eine gewisse Denkstruktur eingeprägt, die es zu Zeiten der Dinosaurier wahrscheinlich nicht gab. |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 25. März 2017 16:13 Titel: |
|
|
| Platonische Mathematik hat Folgendes geschrieben: | | ... und es würden drei Steine zu zwei Stein fallen oder rollen, dann sind es doch fünf Steine. |
Das ist ein Spezialfall der Mathematik. Er gilt z.B. nicht für drei Wassertropfen plus zwei Wassertropfen, die zusammenfallen  |
|
|
Namenloser324
Gast
|
| Namenloser324 Verfasst am: 25. März 2017 19:01 Titel: |
|
|
| Platonische Mathematik hat Folgendes geschrieben: | | Und dass die Gleichung 2 + 2 = 4 nicht erst jetzt gerade in die Existenz getreten ist, klingt doch auch plausibel. Wenn es keine Menschen gäbe und keine intelligenten Geschöpfe im Universum, das heißt keine Struktur eines Gehirns, und es würden drei Steine zu zwei Stein fallen oder rollen, dann sind es doch fünf Steine. Die Mathematik existiert unabhängig von uns. |
Ich will selber nicht groß diskutieren, habe aber über das vor kurzem etwas nachgedacht:
Man sollte hier streng unterscheiden zwischen der Aussage 2 + 2 = 4 verstanden als Abbildung der Bezeichnung der Zusammenführung von 2 Objekten mit 2 Objekten die dann vier Objekte ergeben und der mathematischen abstrahierten Bedeutung von 2 + 2 = 4, die doch aussagt, dass das Symbol 2 mittels Operator "+" verknüpft mit dem Symbol 2 ein anderes Symbol 4 ergibt. Dies ist eigentlich die Mathematik dahinter, würde ich sagen. Die Verknüpfung mit der Realität (zwei steine und zwei steine sind vier steine) war sicherlich die Motivation, jedoch ist die Abstraktion unabhängig davon. Was das Symbol "2" bedeuten soll ist streng genommen ja offen. Ich kann es auch völlig interpretationslos behandeln und einfach Rechenregeln definieren mit denen ich weiterrechne. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 26. März 2017 08:43 Titel: |
|
|
Die Symbole in "2+2=4" sind nur Symbole. Die Bedeutung der Mathematik liegt jedoch nicht in den Symbolen; diese sind lediglich eine Notation. Insofern sind die Symbole "4", "IV", "δ", "||||", ... völlig irrelevant. Oder z.B. dy/dx und f'(x).
Siehe mein o.g. Beispiel der Primzahlzwillinge: wenn ein größter Primzahlzwilling existiert, dann existiert er bereits heute, ohne dass wir ihn kennen, und ohne dass wir Symbole zu seiner Bezeichnung explizit hinschreiben (oder hinschreiben können). Dieser Primzahlzwilling existiert auch dann noch, wenn die Menschheit und die Erde vernichtet sind, er kann jedoch auch von anderen intelligenten Wesen entdeckt werden (oder bereits entdeckt worden sein), und sie werden den selben Wert, also das selbe mathematische Objekt entdecken (bzw. entdeckt gaben).
Das mathematische Objekt
<der Wahrheitsgehalt der Aussage "es existiert ein größter Primzahlzwilling">
hat demzufolge bereits heute einen Wert, den wir lediglich noch nicht kennen und noch entdecken müssen. Das ist eigtl. offensichtlich, weil es sich bereits in Schule mit Rechenaufgaben wie "29 * 7" genau so verhält. Niemand würde auf die Idee kommen, dass die Zahl "203" nicht existiert, bevor der kleine Peter sie nicht ausgerechnet hat.
In der Mathematik existieren mathematische Objekte und Strukturen, die man weder vollständig aufschreiben noch vollständig konstruieren kann. Dennoch existieren diese Strukturen in dem Sinne, dass wir sie erkennen und ihre Eigenschaften sowie Relationen untereinander erfassen können. Gerade weil wir keinen direkt konstruktiven Zugang haben, aber dennoch mit diesen Strukturen arbeiten können, existieren sie gewissermaßen unabhängig von einer Konstruktion. Und deshalb halte ich wenig von einem Konstruktivismus in der Mathematik; seine Anwendung führt zu einer Reduzierung des strukturellen Reichtums der Mathematik, zu einer Selbstbeschränkung.
Aber das Verbot, Bilder mit Farbe zu malen, führt lediglich zu einer Beschränkung der Malerei, es eliminiert nicht die Existenz der Farbe in der Natur selbst. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 26. März 2017 11:05 Titel: |
|
|
| Brillant hat Folgendes geschrieben: | | Die Mathematik kann nicht ewig sein, weil sie an Intelligenz gebunden ist. |
Die Farbe "Rot" ist auch an Auge und Gehirn gebunden, nicht jedoch die dahinterliegende Wellenlänge.
| Brillant hat Folgendes geschrieben: | | Wo war die Mathematik vor Erschaffung / Erscheinung des Menschen? Wo wird sie sein nach Aussterben der Menschheit? |
"Wo" ist kein zutreffender Begriff, die Mathematik ist nicht in räumlichen Kategorien beschreibbar.
Was stellt sicher, dass wenn zwei Intelligenzen unabhängig voneinander dieselbe mathematische Entdeckung machen, dass es eben dieselbe mathematische Entdeckung ist? Wenn die Menschheit die Primzahlen 2,3,5,7,... entdeckt, und eine außerirdische Zivilisation dieselbe Struktur findet, warum liegt dann tatsächlich dieselbe Struktur vor? Wenn diese Primzahlen lokal räumlich oder zeitlich verortet oder an Intelligenz gebunden wären, dann wäre nicht einsichtig, dass dieselbe Struktur entdeckt oder erfunden wird.
| Brillant hat Folgendes geschrieben: | Ich zweifle. Du addierst ein grafisches Symbol (2) zu einem anderen Symbol (nochmals 2) und bekommst ein drittes grafisches Symbol.
Diese Symbole gab es früher nicht. Wenn du weisst, dass die Römer II und II zusammenzählten, weisst du dann auch, wie das Ergebnis aussehen muss? IIII, ++ oder IV oder noch anders? Die richtige Antwort IV ist für mich unlogisch, weil man ein Streichholz übrig behält. |
Du verwechselst Symbole und Notation mit deren Bedeutung. Die Symbole "||||", "IV" und "4" sind verschieden, die Bedeutung "vier Weingläser" war für Ägypter, Römer und Araber (oder heute für uns) identisch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
mik81
Gast
|
| mik81 Verfasst am: 26. März 2017 13:04 Titel: Morphismus zwischen Mathematik und Wirklichkeit |
|
|
Ich sehe das ganze folgendermaßen: Mathematik und Realität / Wirklichkeit / Wahrheit (wie man es auch nennen mag) sind zwei verschiedene Dinge, die nicht miteinander verwechselt werden dürfen: Seit tausenden von Jahren sind die Menschen daran interessiert, die Wirklichkeit um sie herum zu verstehen, zu formalisieren, vorauszusagen... Die Mathematik bietet dabei ein Hilfsmittel, welches es uns erlaubt, auf Grundlage von Grundannahmen, welche unserer Intuition nach gut auf die Wirklichkeit passen, weitere Aussagen über die Wirklichkeit zu treffen. Die unmittelbare Wirklichkeit (z. B. 1+1=2), wie wir sie intuitiv zu kennen glauben, wird also zunächst auf formale und abstrahierte Grundannahmen bzw. Axiome abgebildet. Manipulieren und operieren wir nun an diesen Grundannahmen mit formalen Regeln, die für uns anschaulich Regeln der Wirklichkeit entsprechen, so bekommen wir ein mathematisches Resultat, was sich nun wieder auf die Wirklichkeit zurück abbilden lässt. Mathematik ist für mich also so etwas wie ein Tuch, welches auf die Wirklichkeit gelegt wird. Verschiebt man nun das Tuch, verändert seine Struktur und nimmt es anschließend wieder weg, so erkennt man, wie sich diese Operationen auf die Wirklichkeit auswirken.
Mathematik und Wirklichkeit sind also erstmal durch nichts miteinander verknüpft; erst ein "Morphismus", der in erster Linie definiert ist durch unsere eigene Interpretation der Zeichen und Symbole der Mathematik, tut dies. Aus diesem Grund spreche ich der Mathematik keine Existenz außerhalb unseres "Geistes" zu, da erst dieser der Mathematik einen Sinn gibt. Kann niemand mehr über Mathematik nachdenken und oben beschriebene (vor allem metasprachliche) Verknüpfungen herstellen, so denke ich, ist die Mathematik nichts weiter als ein reiner Salat aus Symbolen ohne Bedeutung.
Mit freundlichen Grüßen
mik81 |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 26. März 2017 15:50 Titel: Re: Morphismus zwischen Mathematik und Wirklichkeit |
|
|
| mik81 hat Folgendes geschrieben: |
Aus diesem Grund spreche ich der Mathematik keine Existenz außerhalb unseres "Geistes" zu, da erst dieser der Mathematik einen Sinn gibt. Kann niemand mehr über Mathematik nachdenken und oben beschriebene (vor allem metasprachliche) Verknüpfungen herstellen, so denke ich, ist die Mathematik nichts weiter als ein reiner Salat aus Symbolen ohne Bedeutung.
|
Dein Geist ist es auch, der jetzt gerade der Symbolfolge
"Der Mond umkreist die Erde."
einen Sinn gibt. Folgerst du daraus, daß der Mond oder die Erde außerhalb deines Geistes keine Existenz mehr hat? Spielt es für die Existenz des Mondes eine Rolle ob irgendjemand in der Lage ist, eine Verknüpfung zwischen dem Mond und Sätzen, in denen das Wort "Mond" vorkommt, herzustellen?
Genausowenig wie du das Symbol "Mond" oder den Gedanken an den Mond mit dem Mond selbst verwechselst, solltest du das Symbol "2" oder einem Gedanken an die Zahl zwei mit der Zahl zwei verwechseln. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 26. März 2017 19:24 Titel: Re: Morphismus zwischen Mathematik und Wirklichkeit |
|
|
| mik81 hat Folgendes geschrieben: | | Ich sehe das ganze folgendermaßen: Mathematik und Realität / Wirklichkeit / Wahrheit (wie man es auch nennen mag) sind zwei verschiedene Dinge, die nicht miteinander verwechselt werden dürfen. |
Das steht außer Frage, aber es hat hier auch niemand etwas anderes behauptet.
Es geht darum, ob die physikalische Realität die einzige tatsächlich existierende Wirklichkeit ist und ob u.a. deshalb reine Mathematik zwingend an diese physikalische Realität gebunden ist (die sie außerdem beschreibt).
Der platonistische Gedanke besteht u.a. darin, dass es weitere, von der physikalischen Realisierung unabhängige, völlig andere Seinsweisen gibt, die nicht materiell, nicht räumlich und außerzeitlich sind. U.a. die reine Mathematik würde diese "Welt der Ideen" besiedeln; ihre Gegenstände, also mathematische Strukturen, Relationen usw. wären unabhängig von einer physikalischen Realisierung oder gar ihrer Anwendung im Sinne einer Beschreibung der physikalischen Realität existent.
Ich halte diese Metaphysik Platons insbs. bei der reinen Mathematik - die Platon m.W.n. nicht betrachtet hat - für sinnvoll und m.M.n. richtig, mir ist jedoch bewusst, dass diese philosophische Haltung weder beweisbar ist, noch Auswirkungen auf die meisten Entwicklungen oder Anwendungen der Mathematik hat. |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 26. März 2017 22:01 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | "Wo" ist kein zutreffender Begriff, die Mathematik ist nicht in räumlichen Kategorien beschreibbar. |
Wenn die Mathematik keinen Ort hat, wie kann sie dann an die nächste Generation weitergegeben werden?
Der Lehrer hat sie nicht im Gehirn und sie steht auch in keinem Buch?
Die Mathematik, die beim Bau der Pyramiden verwendet wurde, ist nirgendwo aufgeschrieben und kein Lebender hat sie im Kopf. Sie ist verschollen, also nicht vorhanden. Deshalb blühen die wildesten Spekulationen |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 26. März 2017 22:17 Titel: |
|
|
Das ist nicht die Frage.
Wieso können dieselben mathematischen Sätze entdeckt werden, ohne dass die jeweiligen Entdecker am selben Ort und zur selben Zeit leben würden und sich untereinander austauschen?
Und welche Mathematik der Ägypter soll bitte verschollen sein?? |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 26. März 2017 22:19 Titel: Re: Morphismus zwischen Mathematik und Wirklichkeit |
|
|
| index_razor hat Folgendes geschrieben: | | Genausowenig wie du das Symbol "Mond" oder den Gedanken an den Mond mit dem Mond selbst verwechselst, solltest du das Symbol "2" oder einem Gedanken an die Zahl zwei mit der Zahl zwei verwechseln. |
Wir haben doch nur deshalb eine Zahlenreihe, weil wir abzählbare Materie haben, Steine zum Beispiel.
Ich stelle mir einen intelligenten Schleim vor, der im Wasser lebt und nichts abzählen kann:
| Zitat: | | Der Schwarm, erschienen 2004, ist der sechste und erfolgreichste Roman des deutschen Schriftstellers Frank Schätzing. Thema des Science-Fiction-Thrillers ist die existenzielle Bedrohung der Menschheit durch eine unbekannte, intelligente maritime Lebensform. |
Der Schleim hätte vermutlich eine uns vollkommen unbekannte Art der Mathematik. Dann müssen "unsere" Mathematiker "unsere" Mathematik wohl neu definieren.
Auch der Schleim könnte erkennen, dass es Mond und Erde gibt, aber die zu zählen sollte welchen Sinn machen? Zählen wir die Weltalle, in denen wir leben? |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 26. März 2017 22:34 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Wieso können dieselben mathematischen Sätze entdeckt werden, ohne dass die jeweiligen Entdecker am selben Ort und zur selben Zeit leben würden und sich untereinander austauschen? |
Ich will die Leistung von Niemandem klein reden, aber die "Schöpfungshöhe" eines Einzelnen ist doch recht begrenzt, verglichen mit einigen Generationen von Fachleuten.
Das Telefon zum Beispiel wurde etwa zeitgleich von mehreren Menschen erfunden. Vorbedingung war, dass allen die Elektrizität bekannt war, sie hatten also eine gemeinsame. recht hohe Basis.
Das Telefon hätte auch funktioniert, wenn es von einem Steinzeitmenschen erfunden wäre. Aber er hatte nicht die Chance, auf die Arbeit Anderer aufzusetzen.
| TomS hat Folgendes geschrieben: | | Und welche Mathematik der Ägypter soll bitte verschollen sein?? |
Mathematische Kenntnisse über Bauphysik. Baumeister müssen nicht die Ägypter gewesen sein, es gibt Pyramiden weltweit und deren Alter ist strittig. |
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 26. März 2017 23:14 Titel: |
|
|
Wenn ich eine Menge habe und nochmals dieselbe Menge oder irgendeine bestimmte Menge dazu lege dann wird pro Vorgang immer die gleiche gesamte Menge darausresultieren unabhängig davon welchen Zahlenwerte ich den einzlenen Mengen zuordne, was ich zähle und wie ich das Zusammenlegen definiere mit + # oder //() .
Genauso ist egal ob ich zuerst drei Steine hinlege und dann fünf.. oder zuerst fünf und dann drei.
a+b=b+a
Das existiert doch alles unabhängig von der Mathematik
In der Mathematik definiere ich eine Zähllogik und eine Einheit und dann kann ich damit diese Vorgänge beschreiben.
Nach einer anderen Zähllogik oder mit anderen Defintionen wäre 2+2 nie 4 , aber egal welche definitionen es wird derselbe Sachverhalt beschrieben.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 26. März 2017 23:55 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | Wenn ich eine Menge habe und nochmals dieselbe Menge oder irgendeine bestimmte Menge dazu lege dann wird pro Vorgang immer die gleiche gesamte Menge darausresultieren unabhängig davon welchen Zahlenwerte ich den einzlenen Mengen zuordne, was ich zähle und wie ich das Zusammenlegen definiere mit + # oder //() .
Genauso ist egal ob ich zuerst drei Steine hinlege und dann fünf.. oder zuerst fünf und dann drei.
a+b=b+a
Das existiert doch alles unabhängig von der Mathematik. |
Wie bitte?
Diese Erkenntnis, dass das mit Mengen, Steinen, ... funktioniert, dass es letztlich unabhängig von konkreten Objekten, Symbolen und Notationen ist, dass das Kommutativgesetz gilt, das ist im Kern reine Mathematik.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 27. März 2017 06:56 Titel: |
|
|
Ich meine es so. Angenommen es gibt kein intelligentes Lebenwesen, das sich je mit Mengen auseinandersetzt dann würde z.B. das Kommutativgesetz trotzdem gültig sein.
Wenn hier in einem Eimer zuerst 2 Wassertropfen des selben Volumens reinfallen und dann 3 dann wäre dieselbe Menge drinnen wie wenn zuerst 3 und dann 2 reinfallen.
Das ist doch unabhängig davon ob es hier ein intelligentes Lebenwesen gibt, das das ganze dann "Mathematik" nennt oder wie auch immer, welche Symbole und Definitionen es verwendet.
Es sind die selben Gesetzmäßigkeiten die in der Natur verankert sind und beschrieben werden.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 27. März 2017 07:36 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | Angenommen es gibt kein intelligentes Lebenwesen, das sich je mit Mengen auseinandersetzt dann würde z.B. das Kommutativgesetz trotzdem gültig sein.
Wenn hier in einem Eimer zuerst 2 Wassertropfen des selben Volumens reinfallen und dann 3 dann wäre dieselbe Menge drinnen wie wenn zuerst 3 und dann 2 reinfallen.
Das ist doch unabhängig davon ob es hier ein intelligentes Lebenwesen gibt ... |
Ja.
Wobei die Mathematiker sich nicht darauf beziehen, dass die Mathematik physikalisch repräsentiert ist; sie betrachten ja wesentlich allgemeinere mathematische Strukturen, wovon die meisten nichts mit der Natur zu tun haben, sondern als rein abstrakte Entitäten "existieren".
| VeryApe hat Folgendes geschrieben: | | Das ist doch unabhängig davon ... dass das ganze dann "Mathematik" nennt oder wie auch immer, welche Symbole und Definitionen es verwendet. |
Ja.
Aber irgendwie müssen wir das, worüber wir hier diskutieren, ja nennen. Also verwenden wir den Begriff "Mathematik". Natürlich ist das, worauf dieser Begriff Mathematik verweist, weder mit dem Begriff identisch, noch ist die Existenzweise und Gültigkeit dessen in irgendeiner Form von diesem Begriff abhängig (das gilt m.E. jedoch für alle Begriffe, Symbole oder Zeichen; das Bezeichnete ist nie mit dem Zeichen identisch)
| VeryApe hat Folgendes geschrieben: | | Es sind die selben Gesetzmäßigkeiten die in der Natur verankert sind und beschrieben werden. |
Ich wiederhole mich: wobei die Mathematiker gerade nicht davon ausgehen, dass die mathematischen Strukturen und Gesetzmäßigkeiten in der Natur verankert sein müssen. Zum Teil sind sie es - und dann ist es für die Physiker praktisch, für die Mathematiker jedoch nicht essentiell - zum großen Teil sind sie es aber wohl eher nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 27. März 2017 22:33 Titel: |
|
|
| Zitat: | | mathematischen Strukturen |
und darunter fallen jetzt zum Beispiel die komplexen zahlen?
Derem motivationsgrund war doch bei den kubischen Gleichungen - Casus irreducibilis.
also im Prinzip nichts anderes als ein konsequentes Weiterrechnen mit der
 und eine kürzere Schreibweise mit i
Meinst du das zum Beispiel mit mathematische Strukturen, damit ich mir darunter was vorstellen kann.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
|
|
Platonische Mathematik
Gast
|
| Platonische Mathematik Verfasst am: 28. März 2017 20:23 Titel: |
|
|
TomS, basiert denn alles in der reinen Mathematik oder allgemein in der Mathematik auf mathematischen Strukturen? Und muss man sich unter einer mathematischen Struktur etwas anderes vorstellen als ein mathematisches Objekt? Definitionsgemäß gehören zu einer mathematischen Struktur Relationen, also Beziehungen. Sowie die größer oder kleiner Beziehung zwischen zahlen. Aber die Zahlen selbst sind wahrscheinlich mathematische Objekte.
Vielleicht kennst du die Sendung closer to truth, die habe ich mir heute noch mal angeschaut und habe einen Mathematiker und Physiker gesehen, der die platonische Welt bestritten hat. Er sagte, die Mathematik ist abgeleitet von dem Universum, das heißt von der Physik. Das bedeutet, wir haben konkrete und diskrete Zustände im Universum, Atome. Und diese spiegeln die ganzen bzw natürlichen Zahlen wieder. Wenn wir in einem Universum leben, das einer Flüssigkeit ähnelt, dann würde mir eine ganz andere Mathematik haben. Mir fehlt er nicht gesagt das mathematische wissen, um diese Aussage zu falsifizieren oder verifizieren. Was ich aber sagen kann ist, dass Atome nicht der fundamentale Zustand der Natur sind, sondern die Wellengleichung. Und dies ist doch nicht diskret. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 28. März 2017 21:45 Titel: |
|
|
| Platonische Mathematik hat Folgendes geschrieben: | | TomS, basiert denn alles in der reinen Mathematik oder allgemein in der Mathematik auf mathematischen Strukturen? Und muss man sich unter einer mathematischen Struktur etwas anderes vorstellen als ein mathematisches Objekt? Definitionsgemäß gehören zu einer mathematischen Struktur Relationen, also Beziehungen. Sowie die größer oder kleiner Beziehung zwischen zahlen. Aber die Zahlen selbst sind wahrscheinlich mathematische Objekte. |
Eine Zahl würde ich auch als mathematisches Objekt ansehen, aber Mathematik beinhaltet doch bereits im einfachen Fall der natürlichen Zahlen mehr als eine Ansammlung von Zahlen: 2*3=6, 12=2*2*3, 7 ist prim, ... sind ja alles Eigenschaften, die nicht isolierte, einzelne Zahlen sondern Relationen zwischen Zahlen betreffen.
Dass z.B. innerhalb der Struktur der natürlichen Zahlen eine eindeutige Primfaktorzerlegung existiert, kann nicht an einzelnen Zahlen festgemacht werden sondern ist letztlich eine Eigenschaft der natürlichen Zahlen als Ganzes (und es ist keine triviale Eigenschaft, da es andere Zahlensysteme gibt, in denen dies nicht der Fall ist)
| Platonische Mathematik hat Folgendes geschrieben: | | ... und habe einen Mathematiker und Physiker gesehen, der die platonische Welt bestritten hat. Er sagte, die Mathematik ist abgeleitet von dem Universum, das heißt von der Physik. Das bedeutet, wir haben konkrete und diskrete Zustände im Universum, Atome. Und diese spiegeln die ganzen bzw natürlichen Zahlen wieder. Wenn wir in einem Universum leben, das einer Flüssigkeit ähnelt, dann würde mir eine ganz andere Mathematik haben. Mir fehlt er nicht gesagt das mathematische wissen, um diese Aussage zu falsifizieren oder verifizieren. |
Wir wissen doch heute gar nicht, was fundamental ist. Und wir konnten doch sowohl diskrete als auch kontinuierliche Strukturen in der Mathematik entwickeln; welche Mathematik fehlt uns denn z.B. in der Hydrodynamik? und was ist mit Fraktalen, die soetwas wie eine dazwischen liegende Struktur darstellen?
| Platonische Mathematik hat Folgendes geschrieben: | | Was ich aber sagen kann ist, dass Atome nicht der fundamentale Zustand der Natur sind, sondern die Wellengleichung. Und dies ist doch nicht diskret. |
In der Quantenfeldtheorie haben wir "kontinuierliche" operatorwertige Differentialgleichungen sowie Hilbertraumzustände in separablen Hilberträumen, die eine abzählbare, also diskrete Basis zulassen.
Ich halte diese Argumente - ohne die Sendung gesehen zu haben und ohne den Kollegen zu kennen - für schwach.
Zuletzt bearbeitet von TomS am 28. März 2017 22:34, insgesamt 2-mal bearbeitet |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 28. März 2017 21:45 Titel: |
|
|
| Brillant hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Genausowenig wie du das Symbol "Mond" oder den Gedanken an den Mond mit dem Mond selbst verwechselst, solltest du das Symbol "2" oder einem Gedanken an die Zahl zwei mit der Zahl zwei verwechseln. |
|
Zunächst mal sollten wir uns einig sein, daß das Symbol "2" etwas anderes ist als die Zahl zwei. Darum ging es hier nur. Ob die Zahl zwei (oder andere mathematische Objekte) dann existieren ist eine andere Frage.
| Zitat: |
Wir haben doch nur deshalb eine Zahlenreihe, weil wir abzählbare Materie haben, Steine zum Beispiel.
|
Nein, abzählbar sind sowohl materielle, wie auch immaterielle Dinge, z.B. imaginäre Schäfchen, Sekunden oder die Menge der korrekten Beweise innerhalb der Peano-Arithmetik. Selbst Zahlen kann man zählen. Keiner dieser Tatsachen verdanken wir die Existenz natürlicher Zahlen selbst. Im Gegenteil. Wie kommst du darauf das Zählen von Steinen oder Schäfchen hätte irgendeinen Sinn, wenn es keine natürlichen Zahlen gäbe? Das Zählen bestimmter Objekte konstatiert das Vorliegen einer umkehrbar eindeutigen Paarung dieser Objekte mit den Elementen einer Menge 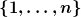 . Implizit in dieser Behauptung sind u.a. einige Existenzaussagen über natürlich Zahlen, z.B. "Zu jedem meiner Objekte existiert eine Zahl k <= n". Oder "Für verschiedene Objekte existieren verschiedene solcher Zahlen." etc. Wenn du also glaubst die Aussage "Vor mir liegen 5 Steine" entspräche der Wahrheit, dann kannst du nicht umhin, die Existenz natürlicher Zahlen zu akzeptieren, von der diese Aussage logisch abhängt.
| Zitat: |
Ich stelle mir einen intelligenten Schleim vor, der im Wasser lebt und nichts abzählen kann:
| Zitat: | | Der Schwarm, erschienen 2004, ist der sechste und erfolgreichste Roman des deutschen Schriftstellers Frank Schätzing. Thema des Science-Fiction-Thrillers ist die existenzielle Bedrohung der Menschheit durch eine unbekannte, intelligente maritime Lebensform. |
Der Schleim hätte vermutlich eine uns vollkommen unbekannte Art der Mathematik. Dann müssen "unsere" Mathematiker "unsere" Mathematik wohl neu definieren.
|
Weil ein Schleim nicht zählen kann, müssen wir die Mathematik umdefinieren? Da kann ich nicht ganz folgen.
| Zitat: |
Auch der Schleim könnte erkennen, dass es Mond und Erde gibt, aber die zu zählen sollte welchen Sinn machen?
|
Ich kann nicht erkennen wofür das relevant sein soll. Die Existenz des Mondes hängt nun gerade nicht davon ab, ob irgendein Schleim ihn erkennen kann. Warum sollte das bei Zahlen anders sein? Es gibt genug Lebewesen, auch außerhalb von Science-Fiction, die sich der Existenz des Mondes wahrscheinlich nicht bewußt sind. Daß du irgendwelche Aliens postulieren kannst, die nichts über Zahlen wissen, beweist überhaupt nichts.
| Zitat: | | Zählen wir die Weltalle, in denen wir leben? |
Warum nicht? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 28. März 2017 22:40 Titel: |
|
|
Der Schleim würde evtl. zunächst andere Teilbereiche der Mathematik erkunden als wir, aber er würde - genügend Intelligenz vorausgesetzt - letztlich zu diskreten Strukturen gelangen.
Z.B. könnte der Schleim seine durch Planetenbeben hervorgerufenen Dichtewellen analysieren. Dabei würde er sinnvollerweise die Kugelflächenfunktionen verwenden - und diese bilden ein abzählbares Funktionensystem.
Aber das beweist letztlich nichts. Ich bin - persönlich - davon überzeugt, dass Existenz i.A. nicht von Erkenntnis abhängt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Platonische Mathematik
Gast
|
| Platonische Mathematik Verfasst am: 29. März 2017 11:52 Titel: |
|
|
TomS, du hast uns m.M.n. immer noch nicht verraten, was die überzeugendsten Argumente für den mathematischen Platonismus sind.
Es müssen doch ein paar Argumente geben, die dich als Physiker davon überzeugen.
Es gibt einen Vortrag auf Youtube zu diesem Thema, leider nur sehr kurz, und dort sagt der Philosoph, dass die meisten Mathematiker - quasi naiverweise - zu einer seiner Ansicht nach richtigen Überzeugung kommen, nämlich der platonischen Sichtweise.
Ich kann man ein paar Argumente oder Dinge, nennen, die mich vom mathematischen Platonismus überzeugen. Vielleicht kannst du was dazu sagen.
1. "Erfindung" der Zahl i als Wurzel von minus 1 erwies sich als fumdenataler Bestandteil der Natur (der Quantenmechanik).
2. Warum sollte eine Gleichung/Zahl erst in die Existenz treten, wenn man daran denkt? Einfach absurd!
3. Das Universum ist durch und durch mathematisch aufgebaut!
4. Bereiche der reinen Mathematik erweisen sich Jahrzehnte später in der Physik als äußerst sinnvoll und auch in der Natur vorhanden.
5. Die Mathematik ist reicher als die Natur. Das spricht doch für deren erste Existenz, woraus erst später die physikalische Welt folgt.
Punkt 5 bedeutet doch, dass selbst ein Universum, dass sich nicht diskret sondern kontinuierlich verhält, wie eine Flüssigkeit, von der Mathematik beschrieben werden kann. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 29. März 2017 14:51 Titel: |
|
|
Ich hatte diese Ideen schon in meine Argumentation eingestreut; Stichworte:
Für viele Mathematiker fühlt sich Mathematik als Entdeckung an, nicht als Erfindung
Mathematik ist omnipräsent
Wenn Mathematik nicht unabhängig von uns "existent" wäre, dann ist völlig unverständlich, warum wir ihr ständig begegnen
Einfache Definition einer mathematischen Struktur (Axiome) ergibt ein extreme reichhaltiges Bild an Eigenschaften, Theoremen, Querbeziehungen, ... ohne dass dies vorher in die Defintion hineingesteckt worden wäre |
|
|
Platonische Mathematik
Gast
|
| Platonische Mathematik Verfasst am: 29. März 2017 17:07 Titel: |
|
|
|
TomS, glaubst du denn, dass Mathematik das Universum (oder alle Universen) instantiiert hat? Wenn Mathematik bzw mathematische Objekte und Strukturen zeitlos, und gleichzeitig überall und nirgendwo existieren, dann könnte es doch sein, dass die Mathematik als immaterielles Reich der Möglichkeiten das Universum in seine Existenz geworfen hat. Oder alles ist nur Mathematik, eine ziemlich extreme Ansicht von Max Tegmark. Klingt auf jeden Fall revolutionär. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 29. März 2017 18:06 Titel: |
|
|
| Platonische Mathematik hat Folgendes geschrieben: | TomS, du hast uns m.M.n. immer noch nicht verraten, was die überzeugendsten Argumente für den mathematischen Platonismus sind.
Es müssen doch ein paar Argumente geben, die dich als Physiker davon überzeugen.
Es gibt einen Vortrag auf Youtube zu diesem Thema, leider nur sehr kurz, und dort sagt der Philosoph, dass die meisten Mathematiker - quasi naiverweise - zu einer seiner Ansicht nach richtigen Überzeugung kommen, nämlich der platonischen Sichtweise.
|
Die primäre Frage ist, ob mathematische Strukturen überhaupt existieren. Das beste Argument dafür ist m.E. die vollkommene Absurdität der Gegenposition. Wer bestreitet, daß z.B. die natürlichen Zahlen in der einen oder anderen Form existieren, kann nicht gleichzeitig glauben, daß die Frage "Ist 1009 die kleinste Primzahl größer als 1000?" sinnvoll zu beantworten ist. Die meisten Menschen mit mathematischer Grundbildung dürften aber, unabhängig von einer eventuellen Neigung zum Hyperskeptizismus sogar wissen, wie man die entsprechende Behauptung verifiziert. Sie würden auch wissen, daß z.B. 1008 nicht die kleinste Primzahl größer 1000 ist und warum nicht.
Absurd ist es nun, anzunehmen, es wäre möglich etwas über die Eigenschaften nicht-existierender Dinge herauszufinden. Wenn es sich bei den natürlichen Zahlen um Fiktionen handeln würde, könnten wir allenfalls Eigenschaften von ihnen erfinden, aber nicht herausfinden welche zutreffen und welche nicht. Wir können die Eigenschaften natürlicher Zahlen aber genauso wenig erfinden, wie die von Mond und Erde. Vergleiche in diesem Zusammenhang jedes beliebige mathematische Problem mit jenem, herauszufinden ob, sagen wir, Pegasus höher fliegen kann, als eine Boeing oder wie viele Engel auf eine Nadelspitze passen und du merkst sofort, wie sich der Unterschied zwischen Existenz und Nichtexistenz anfühlt. (Wie würde man überhaupt anfangen die Eigenschaften von Pegasus zu untersuchen?)
Nicht zu vergessen gibt es auch positive Beweise für die Existenz mathematischer Strukturen. Selbst wenn du dich nicht von Anfang an ontologisch festlegen willst, kannst du folgendes tun: Schreibe irgendeine beliebige Menge von Axiomen auf. Achte nur darauf, daß du keine Widersprüche einbaust. Dann folgt aus Gödels Vollständigkeitssatz, daß es irgendeine mathematische Struktur gibt, auf die alle Axiome zutreffen. Ungefähr so folgt z.B. auch die Existenz natürlicher Zahlen: Bewiesenermaßen sind die Peano-Axiome widerspruchsfrei. Also gibt es Modelle, die sie erfüllen. Also gibt es auch ein kleinstes Modell, das sie erfüllt. Das sind nach gängiger Vorstellung genau die natürlichen Zahlen. Natürlich kannst du wiederum alles mögliche an diesem Argument bestreiten, wie z.B. den Beweis der Widerspruchsfreiheit der Peano-Axiome. Aber bestreiten kannst du letztendlich alles und hier handelt es sich dann nicht mehr um ein spezielles Problem der Mathematik, sondern um eines der Erkenntnistheorie im allgemeinen. Wo da eine vernünftige Grenze zwischen Skeptizismus und Naivität verläuft, ist immer eine Ermessensfrage. Aber sie läuft mit Sicherheit nicht genau zwischen mathematischen und nicht-mathematischen Objekten.
Also gehen wir mal davon aus, es existieren einige mathematische Objekte. Die sekundäre Frage ist, in welcher Form sie existieren -- für sich selbst, in unserem Geist, irgendwie innerhalb des physikalischen Universums oder wie auch immer. Diese Frage ist m.E. falsch formuliert und bezieht sich gar nicht mehr auf den ontologischen Status dieser Objekte, sondern will einfach wissen welche Eigenschaften mathematische Objekte haben. Die Frage, ob z.B. Zahlen unabhängig von unserem Geist existieren, hat genau denselben Charakter, wie die Frage ob z.B. die Drehgruppe unabhängig von der Translationsgruppe existiert oder ob deine Persönlichkeit unabhängig von Sternenkonstellationen zum Zeitpunkt deiner Geburt existiert. Diese Fragen kann man nur entscheiden, indem man die Eigenschaften der fraglichen Objekte untersucht oder anders gesagt, indem man versucht viele Wahrheiten über diese Objekte herauszufinden. Folgt z.B. aus den Eigenschaften deiner Persönlichkeit das Vorliegen einer bestimmten Konstellation bei deiner Geburt? Sicher nicht. Folgt aus der Existenz von SO(n) die Existenz der Gruppe R^n? Ich denke nicht. (Ehrlich gesagt, weiß ich es nicht.) Folgt aus den Eigenschaften der natürlichen Zahlen die Existenz irgendeines Geistes, der sie sich gerade vorstellt? Folgt die Existenz eines physikalischen Universums mit abzählbarer Materie? Ebenfalls ein ziemliche klares "Nein". Warum bin ich mir da sicher? Keine der unzähligen bekannten arithmetische Wahrheiten nimmt in irgendeiner Form Bezug auf Geist, Materie oder Universum. Niemand käme auf die Idee, zur Klärung der Goldbachschen Vermutung astronomische oder psychologische Untersuchungen anzustellen. Nichts was wir über das physikalische Universum oder unseren Geist erfahren können, brächte uns auch nur einen Schritt näher an eine Entscheidung über die Wahrheit der Goldbachschen Vermutung. Das bedeutet, nach allem was wir über die natürlichen Zahlen wissen, existieren sie unabhängig von Geist, Materie und Universum. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 29. März 2017 22:22 Titel: |
|
|
Schöner Beitrag, dem ich absolut zustimme.
Aber wir wissen natürlich, dass es Gegenpositionen gibt, wie die der Formalisten, die diese Frage letztlich nicht stellen wollen, oder wie die der Intuitionisten, die Mathematik tatsächlich als unser Konstrukt ansehen. Fairerweise müssten wir die zu Wort kommen lassen, um durch Widerlegung ihrer Argumente unsere Position zu stärken. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 29. März 2017 22:39 Titel: |
|
|
| Platonische Mathematik hat Folgendes geschrieben: | | TomS, glaubst du denn, dass Mathematik das Universum (oder alle Universen) instantiiert hat? Wenn Mathematik bzw mathematische Objekte und Strukturen zeitlos, und gleichzeitig überall und nirgendwo existieren, dann könnte es doch sein, dass die Mathematik als immaterielles Reich der Möglichkeiten das Universum in seine Existenz geworfen hat. Oder alles ist nur Mathematik, eine ziemlich extreme Ansicht von Max Tegmark. Klingt auf jeden Fall revolutionär. |
Ich denke, letztlich hat bereits Pythagoras ähnliche Thesen geäußert.
Ich schwanke zwischen revolutionär und trivial. Letztlich geht es darum, warum Mathematik für die Natur eine zutreffende Beschreibung liefert.
Nun kann ich nicht mal sagen, ob das für die gesamte Natur gilt, da ich die Natur des menschlichen Geistes nicht kenne, und sie aufgrund der Selbstbezüglichkeit möglicherweise nicht in einem unseren Geist zugänglichen Modell erfassen kann, dessen Komplexität echt kleiner ist als der Geist selbst.
Dann ist es philosophisch gewagt, zur Beantwortung der Frage nach dem Grund der Isomorphie zweier unterschiedlicher Entitäten in unterschiedlichen Kategorien diese Kategorien zu ignorieren und die Entitäten zu identifizieren. Die Frage, warum du so warmherzig wie ein Frühlingstag bist, löse ich ja nicht dadurch, dass ich dich mit einem Frühlingstag gleichsetze.
Es ist außerdem gewagt, aus einer nicht bestätigten Hypothese die Existenz weiterer Entitäten abzuleiten (viele zweifeln schon an der Existenz der "vielen Welten" nach Everett, obwohl diese formal beweisbar aus der etablierten Quantenmechanik folgen).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 29. März 2017 23:00 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | | Wenn hier in einem Eimer zuerst 2 Wassertropfen des selben Volumens reinfallen und dann 3 dann wäre dieselbe Menge drinnen wie wenn zuerst 3 und dann 2 reinfallen.. |
Mein Gefühl sagt mir, dass das nicht immer stimmen muss. Es gibt Fälle, da spielt die Zeit eine Rolle. Da ist es ein Unterschied, ob ich zuerst A und danach B mache oder umgekehrt.
Kennst du die Aufgabe des Fährmanns, der einen Kohl, eine Ziege und einen Wolf zum anderen Ufer übersetzen soll?
| Zitat: | | Ein Fährmann hat eine Fähre. Er möchte einen Kohlkopf, eine Ziege und einen Wolf von einer Uferseite zur anderen bringen. Er kann auf der Fähre aber nur jeweils einen der drei Gegenstände transportieren. Berücksichtigt werden muß auch, dass wenn der Fährmann nicht dabei ist, die Ziege den Kohl und der Wolf die Ziege fressen würde. Was macht der Fährmann nun, um alle drei Gegenstände (oder Tiere) heil von einem zum anderen Ufer zu bringen? |
Kreative Antworten |
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 29. März 2017 23:28 Titel: |
|
|
kenn ich zwar nicht.
Aber ich würde als erstes die Ziege einpacken auf die andere Seite bringen.
dann zurück den (Kohl oder den Wolf holen) , dann den (Kohl oder den Wolf) zur Ziege bringen und die Ziege sofort wieder einpacken auf die startseite bringen, die Ziege dortlassen und den (Kohl wenn zuvor Wolf mitgenommen oder den Wolf wenn zuvor Kohl mitgenommen) auf die andere Seite bringen.
und zum Schluss hol ich noch die Ziege rüber und wenn die sich dann gegenseitig auf der anderen Seite zerfetzen ist mir das egal.
Was das mit b+a=a+b zu tun haben soll ist mir eigentlich das wahre Rätsel
MFG
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 29. März 2017 23:40 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | | Was das mit b+a=a+b zu tun haben soll ist mir eigentlich das wahre Rätsel. |
Gut, nehmen wir ein abstrakteres Beispiel für Mathematiker, nicht für Fährmänner.
Eine Masse m wird von rechts mit einer Gewehrkugel beschossen. Die Wucht des Geschosses versetzt die Masse um den Weg x. Nun wird sie von links mit derselben Kraft beschossen. Sie rückt also um den Wert x zurück und befindet sich wieder am Ausgangspunkt.
Ob das erste Geschoss von links oder rechts kommt, ist mathematisch gleichwertig.
Nun positionieren wir die Masse an einem Abgrund. Der Abgrund ich rechts. Nun ist es nicht nehr gleichgültig, aus welcher Richtung der erste Schuss kommt. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 30. März 2017 00:46 Titel: |
|
|
|
Addition funktioniert unterschiedlich, je nach dem auf welche Art von Objekten du sie anwendest. Unterschiedliche Arten von Objekten bedeutet auch unterschiedliche Additionsregeln, das ist letztlich trivial. |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 25. Apr 2017 18:59 Titel: |
|
|
| TomS 26. März 2017 08:43 hat Folgendes geschrieben: | | Siehe mein o.g. Beispiel der Primzahlzwillinge: wenn ein größter Primzahlzwilling existiert, dann existiert er bereits heute, ohne dass wir ihn kennen, und ohne dass wir Symbole zu seiner Bezeichnung explizit hinschreiben (oder hinschreiben können). Dieser Primzahlzwilling existiert auch dann noch, wenn die Menschheit und die Erde vernichtet sind, er kann jedoch auch von anderen intelligenten Wesen entdeckt werden (oder bereits entdeckt worden sein), und sie werden den selben Wert, also das selbe mathematische Objekt entdecken (bzw. entdeckt gaben). |
Könnte eine Intelligenz, die binär denkt, eine Primzahl erkennen? Da musst du dieser Intelligenz doch erstmal "Primzahl" definieren. Sie ist ohne Rest nur durch 1 oder sich selbst teilbar. Dann musst du "teilen" definieren.
Hier eine binäre Zahl: 10011010011000111001001
Ist das eine Primzahl? Und wie heisst ihr Zwilling? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 29. Apr 2017 08:52 Titel: |
|
|
Eine Zahl z kann in unterschiedlichen Basen b mit jeweils unterschiedlichen Ziffern a < b dargestellt werden:
}\,b^n)
Die Notation lautet
} = a_{0,(b)}a_{1,(b)}a_{2,(b)}\ldots = (a_{0}a_{1}a_{2}\ldots)_{(b)})
Z.B. haben wir die selbe Zahl
} = 11_{(16)})
bzgl. zweier verschiedener Basen.
Dass diese Zahl z eine Primzahl ist, ist völlig unabhängig von der gewählten Darstellung bzw. von der gewählten Basis b. Und eine Notation in einer bestimmten Basis ändert nichts an der Primzahleigeschaft, und es hilft auch nicht, diese zu erkennen. Die Basis ist völlig irrelevant, da sie in der Definition des Begriffs "Primzahl" nicht vorkommt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
