| Autor |
Nachricht |
annafragt
Anmeldungsdatum: 28.01.2021
Beiträge: 309
|
 annafragt Verfasst am: 31. Aug 2021 20:16 Titel: Fehlerrechnung Probefälle annafragt Verfasst am: 31. Aug 2021 20:16 Titel: Fehlerrechnung Probefälle |
 |
|
Meine Frage:
Hallo zusammen, die Aufgabe lautet:
Man hat eine Probe mit 628 Fällen untersucht. Mit welcher relativen Unsicherheit ist das Ergebnis behaftet?
A) 20 Prozent
B) 5 Prozent
C) 4 Prozent
D) 0,25 Prozent
E) 25 Prozent
Wie kommt man auf das korrekte Ergebnis? Ich hätte einfach 1/628 gerechnet, aber das ist ja scheinbar falsch.
Meine Ideen:
Eine Antwort wäre sehr hilfreich vielen dank |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 31. Aug 2021 23:10 Titel: Myon Verfasst am: 31. Aug 2021 23:10 Titel: |
 |
|
Den Aufgabentext finde ich nicht klar formuliert. Was ist mit „Ergebnis“ gemeint, und was mit „relativer Unsicherheit“? Die relative Unsicherheit (bzw. Standardabweichung) des Mittelwerts der Stichprobe kann man nicht angeben ohne Kenntnis der Standardabweichung der Grundgesamtheit.
Was man sagen kann: die Unsicherheit des Stichprobenmittelwerts ist um den Faktor 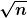 kleiner als die Unsicherheit eines einzelnen Werts der Grundgesamtheit. Hier also wäre die Unsicherheit etwa 4% der Unsicherheit eines einzelnen Werts. kleiner als die Unsicherheit eines einzelnen Werts der Grundgesamtheit. Hier also wäre die Unsicherheit etwa 4% der Unsicherheit eines einzelnen Werts. |
|
 |
annafragt
Anmeldungsdatum: 28.01.2021
Beiträge: 309
|
 annafragt Verfasst am: 01. Sep 2021 14:59 Titel: annafragt Verfasst am: 01. Sep 2021 14:59 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Den Aufgabentext finde ich nicht klar formuliert. Was ist mit „Ergebnis“ gemeint, und was mit „relativer Unsicherheit“? Die relative Unsicherheit (bzw. Standardabweichung) des Mittelwerts der Stichprobe kann man nicht angeben ohne Kenntnis der Standardabweichung der Grundgesamtheit.
Was man sagen kann: die Unsicherheit des Stichprobenmittelwerts ist um den Faktor 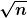 kleiner als die Unsicherheit eines einzelnen Werts der Grundgesamtheit. Hier also wäre die Unsicherheit etwa 4% der Unsicherheit eines einzelnen Werts. kleiner als die Unsicherheit eines einzelnen Werts der Grundgesamtheit. Hier also wäre die Unsicherheit etwa 4% der Unsicherheit eines einzelnen Werts. |
Vielen Dank für die Antwort. Ja die richtige Lösung ist wohl 1/Wurzel aus 628= 4 %
Ich verstehe nur noch nicht ganz wieso man dann 1/ Wurzel aus Anzahl der Fälle rechnet aber wahrscheinlich meint das genau dieses um den Faktor Wurzel aus n kleiner, oder? Vielen dank |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 01. Sep 2021 15:03 Titel: as_string Verfasst am: 01. Sep 2021 15:03 Titel: |
 |
|
Der Messwert ist n und die absolute Unsicherheit ist  . Dann ist die relative Unsicherheit: . Dann ist die relative Unsicherheit:

relativer Unsicherheit ist ja absoluter Unsicherheit geteilt durch Messwert.
Gruß
Marco |
|
 |
annafragt
Anmeldungsdatum: 28.01.2021
Beiträge: 309
|
 annafragt Verfasst am: 01. Sep 2021 15:08 Titel: annafragt Verfasst am: 01. Sep 2021 15:08 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | Der Messwert ist n und die absolute Unsicherheit ist  . Dann ist die relative Unsicherheit: . Dann ist die relative Unsicherheit:

relativer Unsicherheit ist ja absoluter Unsicherheit geteilt durch Messwert.
Gruß
Marco |
Vielen Dank für die Antwort. Tut mir leid, falls das eine blöde Anmerkung ist. Aber woher weiß man, dass die absolute Messunsicherheit Wurzel n ist?
Weil ich dachte die abs Messunsicherheit wäre Standardabweichung : Wurzel n? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 01. Sep 2021 16:21 Titel: as_string Verfasst am: 01. Sep 2021 16:21 Titel: |
 |
|
Bei solchen Zerfallsprozessen geht man ja von einer Poisson-Verteilung aus. Da ist die Varianz gleich dem Erwartungswert, hier also n. Da die Standardabweichung die Wurzel aus der Varianz ist, ist sie eben Wurzel n. Die Standardabweichung ist die absolute Messunsicherheit.
Um eine relative zu bekommen, muss man die absolute durch den Erwartungswert oder bei einer Messung durch den Messwert teilen.
Gruß
Marco |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 01. Sep 2021 16:51 Titel: Myon Verfasst am: 01. Sep 2021 16:51 Titel: |
 |
|
So wie ich den Aufgabentext auffasste, geht es nicht unbedingt um einen Zerfallsprozess. Die Werte müssen auch nicht Poisson-verteilt sein und der Erwartungswert nicht gleich n. Es wird nur gefragt, mit welcher relativen Unsicherheit das „Ergebnis“ der Probe von n „Fällen“ behaftet sei.
Was man (fast) unabhängig von der Verteilung der Werte sagen kann, ist, dass die Unsicherheit um den Faktor 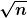 verringert ist, wenn man eine Probe von n Werten hat, verglichen mit einem einzelnen Wert. Das ist aber noch keine Aussage über die relative Unsicherheit. verringert ist, wenn man eine Probe von n Werten hat, verglichen mit einem einzelnen Wert. Das ist aber noch keine Aussage über die relative Unsicherheit. |
|
 |
|















