| Autor |
Nachricht |
Masterchriss
Anmeldungsdatum: 27.12.2004
Beiträge: 95
Wohnort: Köln
|
 Masterchriss Verfasst am: 23. Jun 2007 18:13 Titel: Fehlerrechnung Masterchriss Verfasst am: 23. Jun 2007 18:13 Titel: Fehlerrechnung |
 |
|
Hallo zusammen, hab mal wider ein kleines Problem.
Angenommen ich möchte an einer Drehmoment Berechnung den gesammten Meßfehler berechnen.
Prozeßgleichung:

Mit

Dadurch das der Winkel zwichen Kraft und Hebel nicht genau 90° beträgt, muß in meinem Fehlermodell noch der Winkel miteinbezogen werden.
)
wobei

Wenn ich nun die Partielle ableitungen aufstelle, erhalte für die Ableitung nach x
\cdot M\cdot L)
Und da der Cos von 90° null ist, wird mein Sensitivitätskoeffizient C_x auch null.
Aber es kann doch nicht sein das die Unsicherheit des Winkels vernachlässigt werden kann! Oder?
Wo ist mein Fehler?
Vielen Dank,
Chris |
|
 |
Enthalpus-Laplacus

Anmeldungsdatum: 02.12.2004
Beiträge: 271
Wohnort: Bavaria
|
 Enthalpus-Laplacus Verfasst am: 23. Jun 2007 19:46 Titel: Enthalpus-Laplacus Verfasst am: 23. Jun 2007 19:46 Titel: |
 |
|
Das ist schon korrekt.
Indem Du M nach dem Winkel partiell ableitest bestimmst Du ja seine Änderungsrate abhängig vom Winkel selbst.
d.h. Wie ändert sich M mit dem Winkel.
Wenn Du also jetzt noch die änderungsrate mit dem geschätzten Fehler multiplizierst, kannst Du eine aussage treffen, inwieweit M schwankt (+/-) wenn der Winkel mit einem bestimmten Fehler (oder Unsicherheit) gemessen wurde.
Da aber die Änderungsrate des Sinus abhängig von seinem Argument ja gleich dem Cosinus ist heißt das:
Der Anstieg (Änderungsrate) des Sin wird immer kleiner je näher sich der Winkel 90° nähert.
Der Wert für für die Änderungsrate des sin in der nähe von 90°:
cos(89,99999991°)=1,75*10^(-10)
also extrem gering.
Selbst wenn du einen Großen Fehler beim Messen machst (im Vernünftigen Rahmen natürlich), ist die Auswirkung auf das Ergebniss gering.
Daher ist die Auswirkung des Messfehlers für Winkel nahe 90° gering und geht für 90° gegen Null.
_________________
MfG
Enthalpus |
|
 |
Masterchriss
Anmeldungsdatum: 27.12.2004
Beiträge: 95
Wohnort: Köln
|
 Masterchriss Verfasst am: 23. Jun 2007 20:16 Titel: Masterchriss Verfasst am: 23. Jun 2007 20:16 Titel: |
 |
|
Ok, erstmal vielen Dank für deine Antwort. Musste was länger nachdenken bis ich alles verstanden hatte. Hört sich aber plausiebel an.
Damit ist das problem zwar verstanden, aber noch nicht gelöst.
Nehmen wir mal an F und L haben keinen Fehler. Nur der Winkel lässt sich auf pluminus 10° bestimmen. jetzt versuche ich nur mal den Fehler abzuschätzen indem ich mal 90° einsetze und mal 80°. Das ergebniss unterscheidet sich dann schon um ca 0,15N. ist vieleicht nicht viel, aber ich habe eigentlich ein etwas komplexeres model mit dem selben Problem. Und da geht es darum sehr genau zu arbeiten.
Gibt es dafür noch einen anderen Ansatz als die Gaußsche Fehlerrechnung? Oder sonst irgend einen Lösungsvorschlag?
Gruß |
|
 |
Enthalpus-Laplacus

Anmeldungsdatum: 02.12.2004
Beiträge: 271
Wohnort: Bavaria
|
 Enthalpus-Laplacus Verfasst am: 23. Jun 2007 20:39 Titel: Enthalpus-Laplacus Verfasst am: 23. Jun 2007 20:39 Titel: |
 |
|
Das Fehlerfortpflanzungsgesetz ist nur gültig wenn die Messunsicherheiten recht klein gegen dem Messwert sind und es sich nicht um statistische Fehler handelt.
Daher ist deine Abschätzung mit den 10° außerhalb der Toleranz für dieses Verfahren.
Eigentlich ist das das Standardverfahren. Und es liefert auch recht gute Näherungen für den Fehler bei einer endlichen anzahl von Messwerten.
Wie gesagt es gilt nur solange die Fehler klein gegenüber dem Messwert sind.
Für lineare Funktionen liefert die Abschätzung auch für größere Fehler immer noch gute Werte, enthalten aber die Funktionen nichtlineare Elemente wie sin, cos, ... dann wird die Abschätzung für zunehmende Messfehler immer ungenauer.
Also:
Für zu große Messfehler ist die Fehlerberechnung sinnlos...
_________________
MfG
Enthalpus |
|
 |
Masterchriss
Anmeldungsdatum: 27.12.2004
Beiträge: 95
Wohnort: Köln
|
 Masterchriss Verfasst am: 24. Jun 2007 13:58 Titel: Masterchriss Verfasst am: 24. Jun 2007 13:58 Titel: |
 |
|
Bin jetzt ein wenig verwirrt. Wieso nicht bei Statistischen Fehlern? Ich dachte gerade dafür wäre das Verfahren gedacht.
Z.b kann ich für eine Länge x, duch untersuchungen einer representativen anzahl, eine Streuung bestimmen. Wenn ich nun 2 von idesen Längen addiere verändert sich ja meine Streung. Das bestimme ich mit der Fehlerfortpflanzung.
Oder liege ich Falsch?
Gruß |
|
 |
Enthalpus-Laplacus

Anmeldungsdatum: 02.12.2004
Beiträge: 271
Wohnort: Bavaria
|
 Enthalpus-Laplacus Verfasst am: 24. Jun 2007 15:09 Titel: Enthalpus-Laplacus Verfasst am: 24. Jun 2007 15:09 Titel: |
 |
|
Sorry, wir haben vielleicht etwas aneinander geredet. Ich geb dir hier mal einen Überblick.
Hab mich auch die ganze Zeit auf das arithmetische Fehlerfortpflanzungsgesetz bezogen da ich dachte dass du davon ausgehst.
Bei der Fehlerrechnung kann man von zwei Ansätzen ausgehen:
1. Die Messfehler sind statistisch Unabhängig:
In desem Fall benutzt man das arithmetische Fehlerfortpflanzungsgesetz:
)

Dies kann man z.B. für worst case Abschätzungen des Fehlers machen, also Größtfehlerbestimmung.
2. Für nicht miteinander korrelierte Messwerte und statistisch Abhängige Messfehler:
Hier kommt das bekannte Gaußsche Fehlerfortpflanzungsgesetz ins Spiel:
^2 \cdot\sigma _{x1}^2+\left(\frac{\partial q}{\partial x_2}\right)^2 \cdot\sigma _{x2}^2+...})
 sind hier bei die Varianzen der jweiligen Messgrößen. Also ihre zuflällige Streuung. Man kann auch sagen dass es die Quadrate der Standardabweichung sind!!!! sind hier bei die Varianzen der jweiligen Messgrößen. Also ihre zuflällige Streuung. Man kann auch sagen dass es die Quadrate der Standardabweichung sind!!!!
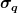 gibt dann die Standardabweichung von q an! Also die mittlere Abweichung vom Erwartungswert. Dies aber nur wahrscheinlichkeitstheoretisch, da hier von unendlich vielen Messwerten ausgegangen wird. gibt dann die Standardabweichung von q an! Also die mittlere Abweichung vom Erwartungswert. Dies aber nur wahrscheinlichkeitstheoretisch, da hier von unendlich vielen Messwerten ausgegangen wird.
Diese Formel gibt den wahrscheinlichen Fehler an!!!
_________________
MfG
Enthalpus |
|
 |
Masterchriss
Anmeldungsdatum: 27.12.2004
Beiträge: 95
Wohnort: Köln
|
 Masterchriss Verfasst am: 24. Jun 2007 16:50 Titel: Masterchriss Verfasst am: 24. Jun 2007 16:50 Titel: |
 |
|
sorry, hatte ich mich wohl nicht richtig ausgedrückt. Muß erlich sagen das ich die erste form noch garnicht kannte.
Kennst du zufällig noch ne gute Seite auf der das Verständlich erklärt ist?
Vielen Dank erst mal...
Gruß Chris |
|
 |
Enthalpus-Laplacus

Anmeldungsdatum: 02.12.2004
Beiträge: 271
Wohnort: Bavaria
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 24. Jun 2007 18:54 Titel: as_string Verfasst am: 24. Jun 2007 18:54 Titel: |
 |
|
Hallo!
Nur, dass es umgekehrt ist: Bei statistisch unabhängigen Messfehlern nimmt man die Gaußsche Fehlerfortpflanzung.
Gruß
Marco |
|
 |
Enthalpus-Laplacus

Anmeldungsdatum: 02.12.2004
Beiträge: 271
Wohnort: Bavaria
|
 Enthalpus-Laplacus Verfasst am: 24. Jun 2007 21:58 Titel: Enthalpus-Laplacus Verfasst am: 24. Jun 2007 21:58 Titel: |
 |
|
Stimmt. Ist genau umgekehrt. Da hab ich was durcheinander gebracht.

Danke as_string
_________________
MfG
Enthalpus |
|
 |
Masterchriss
Anmeldungsdatum: 27.12.2004
Beiträge: 95
Wohnort: Köln
|
 Masterchriss Verfasst am: 26. Jun 2007 11:51 Titel: Masterchriss Verfasst am: 26. Jun 2007 11:51 Titel: |
 |
|
Was muss ich den unter einer Statistischen Abhängigkeit der Messabweichungen verstehen?
Bedeutet das, dass die Abweichungen von einander abhängig sind? Bezeichnet man das nicht auch als Korrelierende Größen?
Bei dem Beispiel mit den Längen das ich genannt hatte, errechne ich die Abweichung mit der Gaußschen Fehlerfortpflanzung, oder?
Dann habe ich immernoch nicht so richtig verstanden wann ich das arithmetische Fehlerfortpflanzungsgesetz benutze.
Sorry wenn das komische Fragen sind, aber das ist ein ganz neues Gebiet für mich und ich versuch gerade noch die Ganze Geschichte irgendwie einzuordnen und zu verstehen.
Danke und Gruß |
|
 |
Enthalpus-Laplacus

Anmeldungsdatum: 02.12.2004
Beiträge: 271
Wohnort: Bavaria
|
 Enthalpus-Laplacus Verfasst am: 26. Jun 2007 15:03 Titel: Enthalpus-Laplacus Verfasst am: 26. Jun 2007 15:03 Titel: |
 |
|
| Masterchriss hat Folgendes geschrieben: | Was muss ich den unter einer Statistischen Abhängigkeit der Messabweichungen verstehen?
Bedeutet das, dass die Abweichungen von einander abhängig sind? Bezeichnet man das nicht auch als Korrelierende Größen? |
Dies bedeutet dass die Messwerte statistisch (= zufällig) schwanken. Man kann die Ursachen der Schwankung im Detail nicht nachvollziehen.
Das Gegenteil hierzu wären systematische Fehler. Also solche die immer wieder auftreten, z.B. weil das Messgerät defekt ist, oder Eine Rückwirkung der Messgrößen auf das Gerät vorkommt usw...
Diese kann man dann auch nachvollziehen und im Bestfall korrigieren.
Die Messwerte dürfen nicht voneinander abhängen, sonst wären sie ja korreliert und somit zusätzlich beeinflusst.
(Jedoch kann man für korellierte Größen im Gaußschen-Fehlerfortpflanzungsgesetz zusätzliche Terme einführen... das nur am Rande)
| Zitat: |
Bei dem Beispiel mit den Längen das ich genannt hatte, errechne ich die Abweichung mit der Gaußschen Fehlerfortpflanzung, oder?
Dann habe ich immernoch nicht so richtig verstanden wann ich das arithmetische Fehlerfortpflanzungsgesetz benutze.
Sorry wenn das komische Fragen sind, aber das ist ein ganz neues Gebiet für mich und ich versuch gerade noch die Ganze Geschichte irgendwie einzuordnen und zu verstehen.
Danke und Gruß |
Das arithmetische Fehlergesetz kannst Du eigentlich immer benutzen.
Damit kannst Du den Größtfehler einer Messung abschätzen
Das Gaußsche Gesetz entsprich einer statistischen Analyse.
Damit bestimmst Du den wahrscheinlichen Fehler bzw. Messunsicherheit...
Lies dir mal zu dem Thema die ersten acht Seiten in dem Skript das ich ober verlinkt habe durch. Dann dürfte dir glaube ich vieles klarer werden.
_________________
MfG
Enthalpus |
|
 |
Masterchriss
Anmeldungsdatum: 27.12.2004
Beiträge: 95
Wohnort: Köln
|
 Masterchriss Verfasst am: 26. Jul 2007 21:30 Titel: Masterchriss Verfasst am: 26. Jul 2007 21:30 Titel: |
 |
|
Also eine Sache ist mir dabei immernoch nicht so ganz klar. Ich geh jetz immernoch von der Fehlerfortpflanzung aus.
Also:
^2 \cdot\sigma _{x1}^2+\left(\frac{\partial q}{\partial x_2}\right)^2 \cdot\sigma _{x2}^2+...})
Warum eigentlich so viel Aufwand betreiben um die Messunsicherheit zu berrechnen, wenn man doch einfach die Messunsicherheit der gesuchten Größe direkt über die Standartabweichung bestimmen kann.
Um noch mal das Beispiel vom Drehmoment aufzunehmen, da müsste man ja erst mal jede Größe, also Kraft, Hebelarm und Winkel untersuchen um die Messunsicherheit zu bestimmen. Dabei würde es ja auch reichen wenn ich nur das Ergebnis, also das Drehmoment untersuche und mit Hilfe der Statistik die standartabweichung bestimme.
Oder ist das eigentlich nur für Messungen gedacht die sehr aufwendig oder Zeitintensiv sind? Oder zur Einfachen Abschätzung vor einem Versuch?
Danke und Gruß,
Chris |
|
 |
Masterchriss
Anmeldungsdatum: 27.12.2004
Beiträge: 95
Wohnort: Köln
|
 Masterchriss Verfasst am: 04. Aug 2007 17:58 Titel: Masterchriss Verfasst am: 04. Aug 2007 17:58 Titel: |
 |
|
Ok, habe die Frage ziemlich doof formuliert. Hab da irgendwie nen Gedanken Fehler gemacht. Eigentlich meinte ich folgendes:
Man kann ja aus allen Messwerten den mittelwert und die Streuung bestimmen, und mit der Fehlerfortpflanzung alle Messunsicherheiten Addieren. Das wäre die übliche Vorgehnsweise nach der Gauß´schen Fehlerforpflanzung.
Alternativ kann man aber auch einfach mit den Messwerten rechnen und den Mittelwert und die Streuung aus dem Ergebnis ermitteln. Dann braucht man ja die Fehlerfortpflanzung eigentlich garnicht anzuwenden.
Wo ist der Unterschied zwischen den beiden Vorgehensweisen? Ist eine Vorgehensweise zu bevorzugen oder sogar falsch?
Wenn unklar ist was ich meine schreibe ich gerne noch mal ein Beispiel dazu.
Danke und Gruß,
Chris |
|
 |
|
















