| Autor |
Nachricht |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 16. März 2021 15:12 Titel: Christoffelsymbole für Parallelverschiebung berechnen manuel459 Verfasst am: 16. März 2021 15:12 Titel: Christoffelsymbole für Parallelverschiebung berechnen |
 |
|
Hallo an alle,
ich habe ein für ein gegebenes Koordinatensystem ko- und kontravariante Basisvektoren berechnet. Sie lauten
=\left(3,5)^T,(1,1)^T\right)) bzw. bzw. =\left(\frac{1}{2}(1,-1)^T,\frac{1}{2}(-3,5)^T\right)) . .
Nun soll ich die Christoffelsymbole für dieses Koordinatensystem für die Parallelverschiebung "mit Dreieck und Lineal" berechnen.
Dazu habe ich einen Vektor  im p-q-Koordinatensystem dargestellt, also im p-q-Koordinatensystem dargestellt, also  und und  berechnet. berechnet.
Um die Christoffelsymbole zu berechnen gehe ich wie folgt vor: Ich verschiebe den Vektor 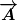 parallel in einen anderen Punkt. Dort hat er die Koordinaten parallel in einen anderen Punkt. Dort hat er die Koordinaten  . .
Nun stecke ich fest. Ich soll nun  und und  als totales Differential der Variablen als totales Differential der Variablen  schreiben und die Parallelverschiebung mathematisch erfassen. schreiben und die Parallelverschiebung mathematisch erfassen.
Ich verstehe nicht mal im Ansatz, was ich hier tun soll. Kann mir da jemand weiterhelfen?
Vielen Dank!
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. März 2021 16:29 Titel: index_razor Verfasst am: 16. März 2021 16:29 Titel: |
 |
|
Die Christoffelsymbole sind eigentlich nur dann ungleich null, wenn sich die Basisvektoren mit dem Ort ändern

Es sieht aber so aus, als wären sie bei dir konstant. In dem Fall wäre die Vorschrift zur Parallelverschiebung ebenfalls trivial:  . Falls das nicht stimmen kann, fehlt m.E. irgendeine Information aus der Aufgabe oder die Lösung ist nicht richtig. . Falls das nicht stimmen kann, fehlt m.E. irgendeine Information aus der Aufgabe oder die Lösung ist nicht richtig.
Wie ist den das Koordinatensystem definiert?
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 16. März 2021 17:36 Titel: manuel459 Verfasst am: 16. März 2021 17:36 Titel: |
 |
|
so:


|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. März 2021 18:14 Titel: index_razor Verfasst am: 16. März 2021 18:14 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | so:

?( |
Da das eine lineare Transformation ist, verschwinden die Christoffelsymbole bzgl. p und q, wenn sie schon bzgl. x und y verschwinden. Sind x und y einfach kartesische Koordinaten in der Ebene? Falls dies so ist, dann bleibt es bei meiner ursprünglichen Antwort: einen Vektor bzgl p, q parallelzuverschieben bedeutet einfach seine Komponenten konstant zu halten. Wenn dir das nicht weiterhilft, mußt du wohl mal den kompletten Aufgabentext posten.
Übrigens, ich erhalte
,\quad\vec{e}_q = \frac{1}{2}(5\vec{e}_x - 3\vec{e}_y)) . .
Einer von uns beiden hat also anscheinend die x- und y-Komponenten vertauscht. (Kann durchaus ich sein.)
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 16. März 2021 23:07 Titel: manuel459 Verfasst am: 16. März 2021 23:07 Titel: |
 |
|
Vielen Dank für deine Antwort. Naja mir kommt das sehr komisch vor - die Aufgabenstellung enthält aber keine weiteren Informationen, außer dass man das Ergebnis dann mit dem allgemeinen Ausdruck für  (mit den ganzen (mit den ganzen 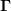 ) vergleichen soll. ) vergleichen soll.
Aber das dürfte auch keine Klarheit bringen.
Und ja, x und y sind karthesische Koordinaten.

Zu den Basisvektoren: Da dürfte ich tatsächlich etwas vertauscht haben. Dein Ergebnis stimmt.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. März 2021 08:44 Titel: index_razor Verfasst am: 17. März 2021 08:44 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | Vielen Dank für deine Antwort. Naja mir kommt das sehr komisch vor - die Aufgabenstellung enthält aber keine weiteren Informationen, außer dass man das Ergebnis dann mit dem allgemeinen Ausdruck für  (mit den ganzen (mit den ganzen 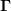 ) vergleichen soll. ) vergleichen soll.
|
Das klingt so, als hättet ihr irgendeine unabhängige Vorschrift zur Bestimmung von  kennengelernt und sollt daraus die Cristoffelsymbole mittels kennengelernt und sollt daraus die Cristoffelsymbole mittels

bestimmen. So wie die Aufgabe gestellt ist, muß natürlich trotzdem  und und  herauskommen. herauskommen.
Was ist denn der "allgemeine Ausdruck" für  und wie habt ihr eigentlich die Christoffelsymbole definiert? und wie habt ihr eigentlich die Christoffelsymbole definiert?
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 17. März 2021 12:44 Titel: manuel459 Verfasst am: 17. März 2021 12:44 Titel: |
 |
|
Ich blicke in diesem ganzen Thema noch kaum durch - hatte erst 2 Stunden Vorlesung dazu.
Jedenfalls haben wir  aufgeschrieben. aufgeschrieben.
Wobei  vermutlich dann einfach die entsprechenden Koordinaten sind und vermutlich dann einfach die entsprechenden Koordinaten sind und 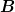 "der Vektor" den man verschiebt. "der Vektor" den man verschiebt.
Was mich etwas verwirrt ist, dass die totale Ableitung in deinen Überlegungen garnicht aufzutauchen scheint. Täuscht mich das?
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 18. März 2021 14:13 Titel: index_razor Verfasst am: 18. März 2021 14:13 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | Ich blicke in diesem ganzen Thema noch kaum durch - hatte erst 2 Stunden Vorlesung dazu.
Jedenfalls haben wir  aufgeschrieben. aufgeschrieben.
Wobei  vermutlich dann einfach die entsprechenden Koordinaten sind und vermutlich dann einfach die entsprechenden Koordinaten sind und 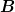 "der Vektor" den man verschiebt. "der Vektor" den man verschiebt.
Was mich etwas verwirrt ist, dass die totale Ableitung in deinen Überlegungen garnicht aufzutauchen scheint. Täuscht mich das? |
Parallelverschiebung entlang einer Kurve im euklidischen Raum bedeutet, daß sich der Vektor nicht ändert, also
 = 0 = \left(\frac{\dd}{\dd t} A^\ell + A^n\Gamma^\ell_{nm} \dot{x}^m\right)\vec{e}_\ell.)
Somit hat

die Form einer totalen Ableitung nach dem Kurvenparameter. Ist das gemeint? Ich sehe allerdings nicht welche Rolle das hier spielen soll, da ja die Zusammenhangskoeffizienten verschwinden. Das bestätigt nochmal  und folglich und folglich ) = \text{const.})
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. März 2021 15:48 Titel: index_razor Verfasst am: 19. März 2021 15:48 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | Was ist denn 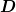 ? Ist das in der ersten Zeile die kovariante Ableitung? ? Ist das in der ersten Zeile die kovariante Ableitung?
|
Ja, das ist die kovariante Ableitung. Dasselbe D steht schon in meiner ersten Antwort. Für einen Vektor  gilt nach den üblichen Ableitungsregeln gilt nach den üblichen Ableitungsregeln
 = \dd A^\ell \vec{e}_\ell + A^\ell D\vec{e}_\ell = ...)
( für Vektorkomponenten und skalare Funktionen.) Der zweite Term für Vektorkomponenten und skalare Funktionen.) Der zweite Term  ergibt die Christoffelsymbole und beschreibt also die Änderung der Basisvektoren. Deswegen tut sich da auch nicht viel, wenn die Basis ortsunabhängig ist. ergibt die Christoffelsymbole und beschreibt also die Änderung der Basisvektoren. Deswegen tut sich da auch nicht viel, wenn die Basis ortsunabhängig ist.
In einer Koordinatenbasis wie hier, gilt

Der erste Term  in der ersten Gleichung ergibt in der ersten Gleichung ergibt

zusammen also
 \vec{e}_\ell \dd x^n \stackrel{\text{def}}{=} A^\ell_{;n} \dd x^n \vec{e}_\ell)
| Zitat: |
Ich poste jetzt doch mal die Aufgabenstellung im Wortlaut. Ich komme nämlich leider auch mit deinen Beiträgen nicht weiter. Da scheint mir ein Grundverständnis zu fehlen das hier bereits vorausgesetzt wird...
:help:
|
Aus meiner Sicht ist es am sinnvollsten die letzte Frage zuerst zu beantworten: Wie kann man Parallelverschiebung mit Dreieck und Lineal mathematisch erfassen?
Möglicherweise übersehe ich es, aber mir scheint dein Skript definiert an keiner Stelle, was "Parallelverschiebung", egal mit welchen Hilfsmitteln, eigentlich mathematisch bedeutet. Es sagt nur, daß es "im Prinzip" eine beliebige Vorschrift ist, die ein Objekt beim Transport von einem Punkt zum anderen "nicht ändert". Das ist allerdings keine besonders gute allgemeine Definition, da sie einerseits wenig informativ ist, und außerdem in gekrümmten Räumen stark an Sinn verliert. Ich finde es jedenfalls verständlich, wenn du allein auf Basis dieser Lektüre noch keine Ahnung hast, was du eigentlich tun sollst.
Die vorausgehende Aufgabe, die  als totales Differential in den Koordinaten zu schreiben, ergibt in dem gegebenen Kontext für mich immer noch keinen Sinn. Vielleicht soll man den Ansatz als totales Differential in den Koordinaten zu schreiben, ergibt in dem gegebenen Kontext für mich immer noch keinen Sinn. Vielleicht soll man den Ansatz
 := A^\ell(x) + \delta A^\ell(x))
machen? Daraus scheint wiederum zu folgen, daß

Aber was soll das ganze? Wenn man sich überlegt, wie man "Parallelverschiebung mittels Geodreieck und Lineal mathematisch erfaßt", dann kommt man doch auch ohne Umschweife dazu, daß in den gegebenen Koordinaten  sein muß. sein muß.
| Zitat: |
Das bisher 2-seitige Skriptum aus der Vorlesung lade ich ungern hier hoch...
Wenn jemand bereit wäre sich meiner Frage nochmals anzunehmen könnte ich das Skriptum aber gerne privat versenden - denn zur Lösung der Frage hilft es höchstens im Hinblick darauf, dass es mein bisheriges gesamtes Wissen zum Thema darstellt und wie es aufgebaut ist (sehr überschaubar und mit großen Lücken im Verständnis für Notation etc.). |
Ich gebe dir recht, daß das Skript bei der Beantwortung der Frage wenig hilft.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. März 2021 14:05 Titel: index_razor Verfasst am: 20. März 2021 14:05 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Aus meiner Sicht ist es am sinnvollsten die letzte Frage zuerst zu beantworten: Wie kann man Parallelverschiebung mit Dreieck und Lineal mathematisch erfassen?
|
Vielleicht noch ein paar Bemerkungen dazu.
Angenommen am Punkt P befinde sich der Vektor 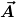 und zeige auf den Punkt P'. Wir wollen und zeige auf den Punkt P'. Wir wollen 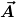 von P nach Q entlang der Gerade von P nach Q entlang der Gerade  transportieren. Wie auch immer wir dabei vorgehen, eine Parallelverschiebung ist dies genau dann, wenn der resultierende Vektor transportieren. Wie auch immer wir dabei vorgehen, eine Parallelverschiebung ist dies genau dann, wenn der resultierende Vektor  auf den Punkt Q' zeigt, so daß PP'QQ' ein Parallelogramm bildet. Es muß also auf den Punkt Q' zeigt, so daß PP'QQ' ein Parallelogramm bildet. Es muß also  und und \cdot \overrightarrow{PQ} = 0) . (Das bedeutet beide Vektoren haben dieselbe Länge und schließen denselben Winkel mit der Geraden ein. Die übliche Konstruktion mittels Lineal und Dreieck versucht genau dies zu erreichen.) Das definiert den Vektor bis auf die Orientierung eindeutig, aber die Orientierung kann sich nicht ändern, wenn wir sagen, daß Parallelverschiebung eine stetige Operation ist. Also gilt . (Das bedeutet beide Vektoren haben dieselbe Länge und schließen denselben Winkel mit der Geraden ein. Die übliche Konstruktion mittels Lineal und Dreieck versucht genau dies zu erreichen.) Das definiert den Vektor bis auf die Orientierung eindeutig, aber die Orientierung kann sich nicht ändern, wenn wir sagen, daß Parallelverschiebung eine stetige Operation ist. Also gilt  . Das entspricht genau der Aussage aus dem Skript, daß Parallelverschiebung den Vektor als "physikalisches Objekt" nicht ändert, die in diesem Fall auch sinnvoll ist. . Das entspricht genau der Aussage aus dem Skript, daß Parallelverschiebung den Vektor als "physikalisches Objekt" nicht ändert, die in diesem Fall auch sinnvoll ist.
Also haben wir 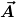 von P nach Q parallelverschoben, wenn wir in Q einfach denselben Vektor von P nach Q parallelverschoben, wenn wir in Q einfach denselben Vektor 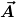 anheften, anheften,  . Die ganze Operation ist in der euklidischen Ebene so trivial, daß kaum zu erkennen ist, daß man überhaupt irgendwas gemacht hat. Sie hat auch offensichtlich gar nichts damit zu tun welche Koordinaten wir den Punkten P und Q oder dem Vektor . Die ganze Operation ist in der euklidischen Ebene so trivial, daß kaum zu erkennen ist, daß man überhaupt irgendwas gemacht hat. Sie hat auch offensichtlich gar nichts damit zu tun welche Koordinaten wir den Punkten P und Q oder dem Vektor 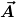 geben. (Und das ist generell der Fall.) geben. (Und das ist generell der Fall.)
Wenn wir aber am Punkt P eine Basis ) wählen, dann können wir den Vektor dort natürlich in seine Komponenten zerlegen, d.h. wählen, dann können wir den Vektor dort natürlich in seine Komponenten zerlegen, d.h.
 \vec{e}_i(P).)
Dasselbe können wir genauso gut im Punkt Q machen. Unter welchen Bedingungen kann der nach Q parallelverschobene Vektor dort nun andere Komponenten ) haben als der ursprüngliche Vektor in P? Da es absolut derselbe Vektor ist, ist dies offenbar nur dann möglich, wenn sich bei Q eine andere Basis befindet. (Also insbesondere die Basis in Q nicht die parallelverschobene Basis aus P ist.) Das ist hier aber nach deinen Angaben nicht der Fall, also gilt haben als der ursprüngliche Vektor in P? Da es absolut derselbe Vektor ist, ist dies offenbar nur dann möglich, wenn sich bei Q eine andere Basis befindet. (Also insbesondere die Basis in Q nicht die parallelverschobene Basis aus P ist.) Das ist hier aber nach deinen Angaben nicht der Fall, also gilt  = A^i(P)) oder oder  . .
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 20. März 2021 14:43 Titel: manuel459 Verfasst am: 20. März 2021 14:43 Titel: |
 |
|
Hallo,
ich glaube es ist mir dank deines letzten Beitrages endlich gelungen zu verstehen was gefragt ist.
Ich habe zunächst wirklich ganz rudimentär die Schreibweise eines totalen Differentials verwendet:  . In dieser Aufgabe wird das zu Folgendem, wenn ich die differentielle Schreibweise mit . In dieser Aufgabe wird das zu Folgendem, wenn ich die differentielle Schreibweise mit 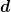 zu einer diskreten mit zu einer diskreten mit  ändere: ändere:
 (analog für (analog für  ) )
Weil wir wegen "parallelverschieben" wissen, dass es keine physikalische Änderung des Vektors gibt, muss die Kovariante Ableitung 0 sein. Deshalb ist die "normale" Ableitung  (die kovariante Ableitung ist lt. Skriptum bekannt). Wir können das nun für (die kovariante Ableitung ist lt. Skriptum bekannt). Wir können das nun für  bzw. bzw.  (und im Gamma dann als (und im Gamma dann als  bzw. bzw.  ) in ) in  einsetzen. einsetzen.
Zum Beispiel setzt man  usw ein. Vergleicht man das mit dem bekannten usw ein. Vergleicht man das mit dem bekannten
 dann ist das genau dasselbe. Wir haben also praktisch auf diesem Weg die Identität dann ist das genau dasselbe. Wir haben also praktisch auf diesem Weg die Identität  hergeleitet. hergeleitet.
Müsste so im Sinne der Aufgabenstellung sein denke ich! Die einzige Frage ist, ob man an der Stelle hier dies Schreibweise  , die ja eigentlich im Sinne der Einsteinschen Summenschreibweise zu lesen ist, auch für einzelne Summanden anwenden darf. , die ja eigentlich im Sinne der Einsteinschen Summenschreibweise zu lesen ist, auch für einzelne Summanden anwenden darf.
An dieser Stelle möchte ich mich einmal herzlich für deine Ausdauer und Hilfsbereitschaft bedanken. Ich bin dadurch einen riesen Schritt weiter gekommen!
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. März 2021 15:18 Titel: index_razor Verfasst am: 20. März 2021 15:18 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: |
Zum Beispiel setzt man  usw ein. usw ein.
Vergleicht man das mit dem bekannten
 dann ist das genau dasselbe. Wir haben also praktisch auf diesem Weg die Identität dann ist das genau dasselbe. Wir haben also praktisch auf diesem Weg die Identität  hergeleitet. hergeleitet.
Müsste so im Sinne der Aufgabenstellung sein denke ich!
|
Ok, aber was mich noch wundert ist folgendes. Die Beziehung, die du gerade hergeleitet hast, gilt für alle Koordinatensysteme. (Denn sie ist ja eine unmittelbare Konsequenz aus  , wie du richtig feststellst, was eine koordinatenunabhängige Bedingung ist.) Was spielt es nun also für eine Rolle, daß wir gerade diese speziellen Koordinaten p und q gegeben haben? Aus dieser speziellen Form der Koordinaten folgt eben auch noch, daß die Christoffelsymbole verschwinden. Aber das kann man viel direkter sehen, als es in der Aufgabe beschrieben ist. , wie du richtig feststellst, was eine koordinatenunabhängige Bedingung ist.) Was spielt es nun also für eine Rolle, daß wir gerade diese speziellen Koordinaten p und q gegeben haben? Aus dieser speziellen Form der Koordinaten folgt eben auch noch, daß die Christoffelsymbole verschwinden. Aber das kann man viel direkter sehen, als es in der Aufgabe beschrieben ist.
Ich habe den Eindruck, die Aufgabe erwartet nun noch eine spezifische Schlußfolgerung über die Christoffelsymbole, vielleicht, indem wir Parallelverschiebung mittels Dreieck und Lineal "mathematisch erfassen". Allerdings finde ich den Teil der Aufgabenstellung so nebulös formuliert, daß ich nicht genau weiß, welche Antwort hier erwartet wird. Die Schlußfolgerung ist mir hingegen völlig klar: die Christoffelsymbole verschwinden und es gilt folglich auch  . .
| Zitat: |
Die einzige Frage ist, ob man an der Stelle hier dies Schreibweise  , die ja eigentlich im Sinne der Einsteinschen Summenschreibweise zu lesen ist, auch für einzelne Summanden anwenden darf. , die ja eigentlich im Sinne der Einsteinschen Summenschreibweise zu lesen ist, auch für einzelne Summanden anwenden darf.
|
Die Frage verstehe ich nicht. Du mußt hier natürlich immer über m summieren, d.h. es gilt z.B.

Und analoges für andere Kombinationen von Vektorkomponenten und partiellen Ableitungen auf der linken Seite.
| Zitat: |
An dieser Stelle möchte ich mich einmal herzlich für deine Ausdauer und Hilfsbereitschaft bedanken. Ich bin dadurch einen riesen Schritt weiter gekommen! |
Es freut mich, wenn es geholfen hat.
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 20. März 2021 16:18 Titel: manuel459 Verfasst am: 20. März 2021 16:18 Titel: |
 |
|
Die Frage bezieht sich darauf, ob ich den Rechenschritt beim  von der Schreibweise von den Differentialquotienten hin zu der mit Gammas richtig gemacht habe. Die Frage war falsch formuliert - da hatte ich falsch gedacht. Trotzdem ist mir noch unklar ob ich den Schritt so machen darf. von der Schreibweise von den Differentialquotienten hin zu der mit Gammas richtig gemacht habe. Die Frage war falsch formuliert - da hatte ich falsch gedacht. Trotzdem ist mir noch unklar ob ich den Schritt so machen darf.
M.a.W: Darf man hier bei  das i (und das k) beispielsweise fixieren/festhalten (als p) und gilt diese Gleichung dann immer noch? Anders komme ich ja nicht dazu, das einsetzen zu dürfen. das i (und das k) beispielsweise fixieren/festhalten (als p) und gilt diese Gleichung dann immer noch? Anders komme ich ja nicht dazu, das einsetzen zu dürfen.
Ich hätte diese "mathematische Fassung" der Parallelverschiebung so als umgesetzt verstanden, indem die kovariante Ableitung als 0 identifiziert wird. Denn so wurde der Parallelverschiebung mathematisch Rechnung getragen. Anderweitig fällt mir da auch nichts ein...
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. März 2021 16:53 Titel: index_razor Verfasst am: 20. März 2021 16:53 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | Die Frage bezieht sich darauf, ob ich den Rechenschritt beim  von der Schreibweise von den Differentialquotienten hin zu der mit Gammas richtig gemacht habe. Die Frage war falsch formuliert - da hatte ich falsch gedacht. Trotzdem ist mir noch unklar ob ich den Schritt so machen darf. von der Schreibweise von den Differentialquotienten hin zu der mit Gammas richtig gemacht habe. Die Frage war falsch formuliert - da hatte ich falsch gedacht. Trotzdem ist mir noch unklar ob ich den Schritt so machen darf.
|
Diese Summe kommt m.E. nirgendwo vor. Oder meinst du  ? ?
Gehen wir nochmal von der Darstellung  aus. Für die kovariante Ableitung schreiben wir aus. Für die kovariante Ableitung schreiben wir
 = \dd A^i \vec{e}_i + A^i D\vec{e}_i \equiv (\dd A^i + \delta A^i)\vec{e}_i,)
m.a.W.  . (Dies definiert die . (Dies definiert die  .) .)
Bei Parallelverschiebung ergibt  den Nullvektor. Da wir es mit einer Basis zu tun haben, gilt dann also komponentenweise den Nullvektor. Da wir es mit einer Basis zu tun haben, gilt dann also komponentenweise

für jedes einzelne i.
Mit parallelverschobener Basis gilt außerdem  , d.h. , d.h.  und deshalb ebenfalls komponentenweise und deshalb ebenfalls komponentenweise

(Und mit der ersten Gl. folgt dann auch  .) .)
| Zitat: |
Ich hätte diese "mathematische Fassung" der Parallelverschiebung so als umgesetzt verstanden, indem die kovariante Ableitung als 0 identifiziert wird. Denn so wurde der Parallelverschiebung mathematisch Rechnung getragen. Anderweitig fällt mir da auch nichts ein... |
Vielleicht interpretiere ich zuviel in die Aufgabe hinein. Aber was hat  mit "Dreieck und Lineal" zu tun? Das ist für mich die Frage. Im Skript wird ja extra betont, daß es mehrere verschiedene formale Definitionen von "Parallelverschiebung" geben kann. Dreieck und Lineal liefern aber ein spezifisches Ergebnis und definieren damit eine bestimmte Vorschrift mit spezifischen Christoffelsymbolen, die man für das gegebene Koordinatensystem mit "Dreieck und Lineal" zu tun? Das ist für mich die Frage. Im Skript wird ja extra betont, daß es mehrere verschiedene formale Definitionen von "Parallelverschiebung" geben kann. Dreieck und Lineal liefern aber ein spezifisches Ergebnis und definieren damit eine bestimmte Vorschrift mit spezifischen Christoffelsymbolen, die man für das gegebene Koordinatensystem  ausrechnen kann. ausrechnen kann.
Wie wird Parallelverschiebung mit Dreieck und Lineal also mathematisch charakterisiert? Meine Antwort weiter oben deutet schon an, daß es wohl etwas damit zu tun hat, das diese Vorschrift der Parallelverschiebung Winkel und Längen von Vektoren unverändert läßt. Wenn der Aufgabensteller gar nichts spezifisches dazu hören wollte, verstehe ich nicht warum hier "Dreiecke" und "Lineale" überhaupt erwähnt werden.
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 20. März 2021 17:27 Titel: manuel459 Verfasst am: 20. März 2021 17:27 Titel: |
 |
|
| Zitat: | | daß es wohl etwas damit zu tun hat, das diese Vorschrift der Parallelverschiebung Winkel und Längen von Vektoren unverändert läßt. |
Genau! Und das kann verwendet werden, wenn die Interpretation der Kovarianten Ableitung einer Koordinaten aus dem Skriptum verwendet wird. Dort steht, dass man diese Kovariante Ableitung einer Koordinate als "die physikalische Änderung der Koordinate" verstehen kann, wenn "man von P nach Q geht". Genau darin liegt meiner Meinung nach die Antwort auf deine Frage, was das mit "Dreieck und Lineal" soll. Es bedeutet, dass sich am Vektor physikalisch nichts ändert. Das wird dadurch klar, dass die Parallelverschiebung als jene mit "Dreieck und Lineal" verstanden wird.
Damit haben wir diese Parallelverschiebung also mathematisch fassbar gemacht, indem wir dazu verwendet haben, dass die Kovariante Ableitung einer Koordinate 0 ist. Denn andere Möglichkeiten die Parallelverschiebung laut Skriptum mathematisch zu fassen gibt es nicht. Lediglich den Weg über "Parallelverschiebung" -> "Parallelverschiebung bedeutet, dass sich physikalisch nichts ändert" -> "Physikalisch nichts ändern bedeutet, dass die Kovariante Ableitung der Koordinate 0 ist" kann ich aus dem Skriptum entnehmen.
Bemerkung: Ich habe unter "Kovarianter Ableitung" bisher das verstanden , was im Skriptum dazu steht - Also die Kovariante Ableitung der Koordinate, geschrieben als  , wobei der Term mit dem Beistrich die "Normale Ableitung" (die man aus der Schule kennt) bezeichnet. Eventuell gab es hier ein begriffliches Missverständnis. , wobei der Term mit dem Beistrich die "Normale Ableitung" (die man aus der Schule kennt) bezeichnet. Eventuell gab es hier ein begriffliches Missverständnis.
Nun zur Frage die ich hatte. Ich glaube ich habe da selbst ein wenig Kauderwelsch fabriziert. Ich versuche es noch einmal. So wie ich die Aufgabe verstehe, soll das Ziel sein,  nachzuweisen. nachzuweisen.
Dazu habe ich die totalen Differentiale aufgeschrieben. Unter der Verwendung der "parallelen Verschiebung" weiß man, dass die Kovariante Ableitung einer Koordinate 0 ist. Mit  finden wir also Ausdrücke, die wir statt den Differentialquotienten (partielle Ableitungen) in den totalen Differenzialen schreiben können. finden wir also Ausdrücke, die wir statt den Differentialquotienten (partielle Ableitungen) in den totalen Differenzialen schreiben können.
Wir setzen also in  ein. Genau hier ist jetzt der Schritt, der mir Bauchschmerzen bereitet. Ich setze nun also ein. Genau hier ist jetzt der Schritt, der mir Bauchschmerzen bereitet. Ich setze nun also  so ein, indem ich so ein, indem ich  und und  bzw. dann in der Notation auch bzw. dann in der Notation auch  setze. Nun setze ich also setze. Nun setze ich also  ein. Analoges für die zweite partielle Ableitung. Dann steht da: ein. Analoges für die zweite partielle Ableitung. Dann steht da:  . Und das ist genau die Schreibweise . Und das ist genau die Schreibweise  die nachzuweisen war (bzw. mit der laut Aufgabenstellung verglichen werden sollte). Ist dieser Rechengang korrekt? die nachzuweisen war (bzw. mit der laut Aufgabenstellung verglichen werden sollte). Ist dieser Rechengang korrekt?
Bemerkung: Eine Kovariante Ableitung als die Ableitung eines Vektors habe ich (siehe Skriptum) meines Wissens nach noch nicht kennengelernt.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. März 2021 18:39 Titel: index_razor Verfasst am: 20. März 2021 18:39 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | Zitat: | | daß es wohl etwas damit zu tun hat, das diese Vorschrift der Parallelverschiebung Winkel und Längen von Vektoren unverändert läßt. |
Genau! Und das kann verwendet werden, wenn die Interpretation der Kovarianten Ableitung einer Koordinaten aus dem Skriptum verwendet wird. Dort steht, dass man diese Kovariante Ableitung einer Koordinate als "die physikalische Änderung der Koordinate" verstehen kann, wenn "man von P nach Q geht". Genau darin liegt meiner Meinung nach die Antwort auf deine Frage, was das mit "Dreieck und Lineal" soll. Es bedeutet, dass sich am Vektor physikalisch nichts ändert. Das wird dadurch klar, dass die Parallelverschiebung als jene mit "Dreieck und Lineal" verstanden wird.
Damit haben wir diese Parallelverschiebung also mathematisch fassbar gemacht, indem wir dazu verwendet haben, dass die Kovariante Ableitung einer Koordinate 0 ist. Denn andere Möglichkeiten die Parallelverschiebung laut Skriptum mathematisch zu fassen gibt es nicht. Lediglich den Weg über "Parallelverschiebung" -> "Parallelverschiebung bedeutet, dass sich physikalisch nichts ändert" -> "Physikalisch nichts ändern bedeutet, dass die Kovariante Ableitung der Koordinate 0 ist" kann ich aus dem Skriptum entnehmen.
|
Ja eben. Das Skript betrachtet die kovariante Ableitung eines Vektors und dessen "physikalische Änderung" als Synonyme. (S. 5 Ende zweiter Absatz) Dies zeichnet also gerade keine spezielle Vorschrift zur Parallelverschiebung aus. Es gibt nämlich beliebig viele kovariante Ableitungen. Aber nur eine definiert eine Parallelverschiebung, die Längen und Winkel unverändert läßt. Und diese ist es, die man mit Dreieck und Lineal bewerkstelligt. Irgendwas stimmt also m.E. an deiner Interpretation nicht. (Es ist natürlich nicht deine Schuld, daß die Aufgabe so vage formuliert ist.)
| Zitat: |
Bemerkung: Ich habe unter "Kovarianter Ableitung" bisher das verstanden , was im Skriptum dazu steht - Also die Kovariante Ableitung der Koordinate, geschrieben als  , wobei der Term mit dem Beistrich die "Normale Ableitung" (die man aus der Schule kennt) bezeichnet. Eventuell gab es hier ein begriffliches Missverständnis. , wobei der Term mit dem Beistrich die "Normale Ableitung" (die man aus der Schule kennt) bezeichnet. Eventuell gab es hier ein begriffliches Missverständnis.
|
Nein, das ist kein Problem. Ich rede lieber von der Komponente der kovarianten Ableitung, als von der kovarianten Ableitung der Komponente (oder Koordinate). Aber gemeint ist dasselbe.
| Zitat: |
Nun zur Frage die ich hatte. Ich glaube ich habe da selbst ein wenig Kauderwelsch fabriziert. Ich versuche es noch einmal. So wie ich die Aufgabe verstehe, soll das Ziel sein,  nachzuweisen. nachzuweisen.
|
Das kann ich mir nicht vorstellen. Erstens stimmt es formal so nicht (siehe Indexbild). Richtig wäre ja

Und das nachzuweisen kann doch nicht die Aufgabe sein, denn das ist Gl. (1) im Skript, die dort letztlich zur Definition von  verwendet wird. Ist das nicht ein bißchen zu trivial? (Andererseits steht bisher auch nicht viel mehr substanzielles im Skript, also vielleicht hast du recht.) verwendet wird. Ist das nicht ein bißchen zu trivial? (Andererseits steht bisher auch nicht viel mehr substanzielles im Skript, also vielleicht hast du recht.)
Der Rest deiner Überlegungen ist, soweit ich sehe, formal richtig. Allerdings bin ich nicht sicher, ob ich dein Problem bei dieser Koordinatensubstitution verstehe. Was du machst ist folgendes: Du hast zwei Koordinaten  . Eine davon nennst du p, die andere q, sagen wir . Eine davon nennst du p, die andere q, sagen wir  . Statt . Statt  und und  schreibst du dann schreibst du dann  und und  . Da passiert nichts mysteriöses. . Da passiert nichts mysteriöses.
Das bedeutet natürlich nicht, daß du irgendwo p=1 und q=2 gesetzt hast. Deshalb ergibt das folgende auch nur zum Teil Sinn:
| Zitat: | Ich setze nun also  so ein, indem ich so ein, indem ich  und und  bzw. dann in der Notation auch bzw. dann in der Notation auch  setze. setze. |
Aber vielleicht hast du dich hier nur ungeschickt ausgedrückt.
| Zitat: |
Bemerkung: Eine Kovariante Ableitung als die Ableitung eines Vektors habe ich (siehe Skriptum) meines Wissens nach noch nicht kennengelernt. |
Das ist aus didaktischer Sicht ein Grundproblem mit dem Skript. (Und mit vielen anderen.) Eine Ableitung von Vektorfeldern (und darauf aufbauend von Tensorfeldern) zu definieren ist der einzige Sinn der Einführung der kovarianten Ableitung. Um nichts anderes geht es dabei eigentlich. Wenn das nicht klar wird, erfüllt das Skript m.E. seine Aufgabe nicht. Es beschreibt zwar den Effekt der kovarianten Ableitung auf Tensorkomponenten, definiert aber nirgendwo was die kovariante Ableitung eigentlich ist. Selbst wenn es dieses Versäumnis später nachholen wird (nicht unbedingt wahrscheinlich), wäre es eine seltsame Reihenfolge der Präsentation.
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 20. März 2021 20:33 Titel: manuel459 Verfasst am: 20. März 2021 20:33 Titel: |
 |
|
Das mit der Frage zur Koordinatensubstitution hat sich geklärt. Ich hab wohl den Wald vor lauter Bäumen nicht mehr gesehen.
| index_razor hat Folgendes geschrieben: |
Ja eben. Das Skript betrachtet die kovariante Ableitung eines Vektors und dessen "physikalische Änderung" als Synonyme. (S. 5 Ende zweiter Absatz) Dies zeichnet also gerade keine spezielle Vorschrift zur Parallelverschiebung aus. Es gibt nämlich beliebig viele kovariante Ableitungen. Aber nur eine definiert eine Parallelverschiebung, die Längen und Winkel unverändert läßt. Und diese ist es, die man mit Dreieck und Lineal bewerkstelligt. Irgendwas stimmt also m.E. an deiner Interpretation nicht. (Es ist natürlich nicht deine Schuld, daß die Aufgabe so vage formuliert ist.) |
Wenn ich dich richtig verstehe (und mir scheint das wird mir erst jetzt richtig bewusst), versuchst du herauszufinden, was eigentlich gesucht ist (in der Aufgabenstellung). Ich stimme dir zu, dass es die Definition aus Gleichung (1) eigentlich wirklich nicht sein dürfte - das wäre ja unsinnig. Es war jedoch ein Versuch meinerseits durch die unmittelbare Anwendung des Skriptes und dem Zusammenführen der einzelnen Hinweise aus der Aufgabenstellung genau das zu erreichen, was am Ende steht (der Vergleich mit der Gleichung (1)).
Nun denn. Es scheint also an der Interpretation von "Parallelverschiebung mit Lineal und Dreieck mathematisch erfassen" zu scheitern. Das hast du hier auf den Punkt gebracht:
| Zitat: | | Ich habe den Eindruck, die Aufgabe erwartet nun noch eine spezifische Schlußfolgerung über die Christoffelsymbole, vielleicht, indem wir Parallelverschiebung mittels Dreieck und Lineal "mathematisch erfassen". Allerdings finde ich den Teil der Aufgabenstellung so nebulös formuliert, daß ich nicht genau weiß, welche Antwort hier erwartet wird. Die Schlußfolgerung ist mir hingegen völlig klar: die Christoffelsymbole verschwinden |
Was mir jetzt noch einfällt, ist das totale Differential und "eine irgendwie geartete, unbekannte mathematische Formulierung der Parallelverschiebung" sofern zusammenzubasteln, dass herauskommt, dass  herauskommt und wir daraus schließen, dass die Christoffelsymbole 0 sind. Diese Formulierung der Parallelverschiebung scheint es aber nicht zu geben - wenn nicht einmal du weißt, wie so etwas aussehen sollte. Mir fällt dazu leider auch nichts ein. Die Kovariante Ableitung dürfte man ja wohl nicht verwenden. Das wäre schummeln. herauskommt und wir daraus schließen, dass die Christoffelsymbole 0 sind. Diese Formulierung der Parallelverschiebung scheint es aber nicht zu geben - wenn nicht einmal du weißt, wie so etwas aussehen sollte. Mir fällt dazu leider auch nichts ein. Die Kovariante Ableitung dürfte man ja wohl nicht verwenden. Das wäre schummeln.
Wie du bereits gezeigt hast, geht all das auch ohne diesen komischen Weg (Aber was genau ist dabei nochmal das springende Argument - dass die zeitliche Ableitung von  null ist, wie in deinem Beitrag vom 18. März (14:13)?) null ist, wie in deinem Beitrag vom 18. März (14:13)?)
Es scheint mir aber, dass wir an dieser Stelle nicht wirklich weiterkommen. Ich würde es also gut verstehen, wenn du sagen würdest, dass es hier aus diesen Umständen nichts weiter zu diskutieren gibt.
Liebe Grüße
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. März 2021 20:35 Titel: index_razor Verfasst am: 20. März 2021 20:35 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | Bemerkung: Eine Kovariante Ableitung als die Ableitung eines Vektors habe ich (siehe Skriptum) meines Wissens nach noch nicht kennengelernt. |
Vielleicht sollten wir den Punkt noch etwas weiter beleuchten. Auch wenn das Skript es nicht deutlich macht, seine grundlegende Definition der kovarianten Ableitung

führt diese als eine Operation auf Vektorfeldern ein. Und zwar sagt (oder eher "impliziert") es folgendes:
Die kovariante Ableitung des Vektorfeldes 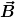 mit den Komponenten mit den Komponenten  bzgl. der Basis bzgl. der Basis 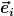 in Richtung des Basisvektors in Richtung des Basisvektors  ist das Vektorfeld genannt " ist das Vektorfeld genannt " " mit den Komponenten " mit den Komponenten  bzgl. derselben Basis bzgl. derselben Basis 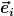 . .
Setzen wir den Vektor wieder zusammen, gilt also
\vec{e}_i)
Insbesondere können wir ohne Probleme nach der kovarianten Ableitung eines Basisvektorfeldes 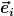 (letztendlich ein ganz normales Vektorfeld) in Richtung eines anderen Basisvektors fragen. Die Komponenten von (letztendlich ein ganz normales Vektorfeld) in Richtung eines anderen Basisvektors fragen. Die Komponenten von 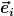 bzgl. der Basis bzgl. der Basis  sind natürlich einfach die konstanten Funktionen sind natürlich einfach die konstanten Funktionen  , also , also 
Wegen

für alle k, i folgt also aus der Definition sofort

Die Christoffelsymbole sind also nichts anderes als die Komponenten der Ableitung des i-ten Basisvektors in Richtung des k-ten Basisvektors bzgl. derselben Basis. Sie tauchen also nur auf, wenn die Basisvektoren nicht "kovariant konstant" sind. Die ursprüngliche Definition ist also äquivalent zu

Und das wiederum bedeutet, daß die kovariante Ableitung linear ist und die Produktregel
 = \left(\partial_{\vec{e}_k} f\right) \vec{X} + f \left(D_{\vec{e}_k}\vec{X}\right))
erfüllt, wobei  die normale Ableitung ist, "die man aus der Schule kennt". Denn die Basisentwicklung die normale Ableitung ist, "die man aus der Schule kennt". Denn die Basisentwicklung  ist nichts anderes als eine Summe von Produkten der Form ist nichts anderes als eine Summe von Produkten der Form  aus skalarer Funktion und Vektor, die hier jeweils die Rolle der "Komponente" bzw. des "Basiselements" übernehmen (was aber ansonsten keine tiefere mathematische Bedeutung hat). aus skalarer Funktion und Vektor, die hier jeweils die Rolle der "Komponente" bzw. des "Basiselements" übernehmen (was aber ansonsten keine tiefere mathematische Bedeutung hat).
***
Bisher hatte diese Operation D übrigens nicht den geringsten Zusammenhang zu Winkeln und Längen der beteiligten Vektoren. Um zu gewährleisten, daß  impliziert, daß impliziert, daß 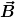 weder seine Länge, noch den Winkel zu anderen parallelverschobenen Vektoren ändert, muß man für D die Eigenschaft der "Metrikverträglichkeit" fordern. Nur dann entspricht die abstrakte Bedingung weder seine Länge, noch den Winkel zu anderen parallelverschobenen Vektoren ändert, muß man für D die Eigenschaft der "Metrikverträglichkeit" fordern. Nur dann entspricht die abstrakte Bedingung  der Parallelverschiebung "mit Dreieck und Lineal" (des Vektors der Parallelverschiebung "mit Dreieck und Lineal" (des Vektors 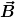 entlang der Kurve mit Tangente entlang der Kurve mit Tangente 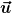 ). ).
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 21. März 2021 11:05 Titel: index_razor Verfasst am: 21. März 2021 11:05 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: |
Nun denn. Es scheint also an der Interpretation von "Parallelverschiebung mit Lineal und Dreieck mathematisch erfassen" zu scheitern. Das hast du hier auf den Punkt gebracht:
| Zitat: | | Ich habe den Eindruck, die Aufgabe erwartet nun noch eine spezifische Schlußfolgerung über die Christoffelsymbole, vielleicht, indem wir Parallelverschiebung mittels Dreieck und Lineal "mathematisch erfassen". Allerdings finde ich den Teil der Aufgabenstellung so nebulös formuliert, daß ich nicht genau weiß, welche Antwort hier erwartet wird. Die Schlußfolgerung ist mir hingegen völlig klar: die Christoffelsymbole verschwinden |
Was mir jetzt noch einfällt, ist das totale Differential und "eine irgendwie geartete, unbekannte mathematische Formulierung der Parallelverschiebung" sofern zusammenzubasteln, dass herauskommt, dass  herauskommt und wir daraus schließen, dass die Christoffelsymbole 0 sind. Diese Formulierung der Parallelverschiebung scheint es aber nicht zu geben - wenn nicht einmal du weißt, wie so etwas aussehen sollte. Mir fällt dazu leider auch nichts ein. Die Kovariante Ableitung dürfte man ja wohl nicht verwenden. Das wäre schummeln. herauskommt und wir daraus schließen, dass die Christoffelsymbole 0 sind. Diese Formulierung der Parallelverschiebung scheint es aber nicht zu geben - wenn nicht einmal du weißt, wie so etwas aussehen sollte. Mir fällt dazu leider auch nichts ein. Die Kovariante Ableitung dürfte man ja wohl nicht verwenden. Das wäre schummeln.
|
Ich glaube hier liegt noch irgendein Mißverständnis vor. Da "Lineal und Dreieck" erwähnt werden, ist mit Sicherheit von der euklidischen Ebene die Rede. In dieser Ebene ist es sinnvoll davon zu sprechen, daß zwei Vektoren an verschiedenen Punkten P und Q identisch sind. (Das ist auf allgemeinen Mannigfaltigkeiten nicht sinnvoll.) Damit gibt es auch eine absolut triviale Vorschrift zur Parallelverschiebung des Vektors 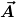 bei P entlang einer beliebigen Kurve bei P entlang einer beliebigen Kurve ) nach Q, nämlich nach Q, nämlich ) = \vec{A}) . Dadurch ist auch die kovariante Ableitung trivial: es handelt sich wieder um die "normale Ableitung, die man aus der Schule kennt", nur eben für vektorwertige Funktionen. Das heißt in Richtung des Tangentenvektors . Dadurch ist auch die kovariante Ableitung trivial: es handelt sich wieder um die "normale Ableitung, die man aus der Schule kennt", nur eben für vektorwertige Funktionen. Das heißt in Richtung des Tangentenvektors  bei t=0 an die Kurve bei t=0 an die Kurve ) definiert man definiert man
) - \vec{A}(c(0)) \qquad\text{(KA)})
bzw. in Richtung eines Basisvektors am Punkt P
 - \vec{A}(P)).)
Falls der Vektor parallelverschoben wird ist er konstant ) = \vec{A}) und es folgt und es folgt  , wie es sein soll. Nach der Kettenregel für die gewöhnliche Ableitung gilt , wie es sein soll. Nach der Kettenregel für die gewöhnliche Ableitung gilt
)|_{t=0} = \nabla\vec{A}(c(0))\cdot \dot{c}(0).)
Die rechte Seite in (KA) hängt also wirklich nur vom Tangentialvektor an der Stelle t=0 ab, genau wie die linke Seite suggeriert.
Da die Vorschrift ) = \vec{A}) den ganzen Vektor unverändert läßt, läßt sie natürlich auch Längen und Winkel von parallelverschobenen Vektoren unverändert. Die Konstruktion mit Dreieck und Lineal hat dieselben Eigenschaften. Umgekehrt kann man aus Eigenschaften der Parallelverschiebung mit Dreieck und Lineal ableiten, daß den ganzen Vektor unverändert läßt, läßt sie natürlich auch Längen und Winkel von parallelverschobenen Vektoren unverändert. Die Konstruktion mit Dreieck und Lineal hat dieselben Eigenschaften. Umgekehrt kann man aus Eigenschaften der Parallelverschiebung mit Dreieck und Lineal ableiten, daß ) = \vec{A}) zumindest entlang von Geraden zumindest entlang von Geraden  = P + t\overrightarrow{PQ}) gelten muß. (Das habe ich weiter oben versucht zumindest plausibel zu machen.) Zu guter Letzt gibt es noch das Levi-Civita-Theorem über die Eindeutigkeit der metrikverträglichen, torsionsfreien kovarianten Ableitung (auch Fundamentalsatz der Riemannschen Geometrie). Für etwas anderes als torsionsfreie kovariante Ableitungen interessieren sich Physiker in diesem Zusammenhang ohnehin nicht. Deswegen können wir mit absoluter Sicherheit davon ausgehen, daß hier die kovariante Ableitung (KA), also die normale vektorielle Ableitung aus der Schule gemeint ist. gelten muß. (Das habe ich weiter oben versucht zumindest plausibel zu machen.) Zu guter Letzt gibt es noch das Levi-Civita-Theorem über die Eindeutigkeit der metrikverträglichen, torsionsfreien kovarianten Ableitung (auch Fundamentalsatz der Riemannschen Geometrie). Für etwas anderes als torsionsfreie kovariante Ableitungen interessieren sich Physiker in diesem Zusammenhang ohnehin nicht. Deswegen können wir mit absoluter Sicherheit davon ausgehen, daß hier die kovariante Ableitung (KA), also die normale vektorielle Ableitung aus der Schule gemeint ist.
Das Skript schreibt die Definition dieser Ableitung zwar beinahe selbst hin und erwähnt später, daß man Parallelverschiebung im Euklidischen Raum mit Lineal und Dreieck zustande bringen kann, geht dann aber nicht weiter auf diesen Zusammenhang ein. Auf S. 5 steht als Definition der Beschleunigung folgender Grenzwert
 = \lim_{\Delta t\to 0}\frac{\vec{v}(t+\Delta t) - \vec{v}(t)}{\Delta t}) . .
Im allgemeinen befindet sich das Teilchen zum Zeitpunkt  nicht mehr am selben Ort wie zur Zeit nicht mehr am selben Ort wie zur Zeit  . Die beiden Tagentialvektoren . Die beiden Tagentialvektoren ) und und ) befinden sich also natürlicherweise ebenfalls an verschiedenen Orten. Trotzdem ist es kein Problem sie voneinander abzuziehen. Denn Newtonsche Mechanik findet im Euklidischen Raum statt und darin gibt es eine triviale Vorschrift zur Parallelverschiebung von Vektoren. befinden sich also natürlicherweise ebenfalls an verschiedenen Orten. Trotzdem ist es kein Problem sie voneinander abzuziehen. Denn Newtonsche Mechanik findet im Euklidischen Raum statt und darin gibt es eine triviale Vorschrift zur Parallelverschiebung von Vektoren.
Hinter der Definition der Beschleunigung steckt also schon immer der Begriff der kovarianten Ableitung. Nur merkt man davon in der Newtonschen Mechanik nichts, weil der absolute Raum euklidisch ist.
Bevor ich nochmal zu den Christoffelsymbolen komme, will ich noch betonen, daß in diesen Überlegungen bereits die Antwort auf die Übungsaufgabe enthalten ist. Parallelverschiebung des Vektors 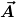 im Euklidischen Raum bedeutet im Euklidischen Raum bedeutet
 = \vec{A}(P))
Also insbesondere (t=1)
 = \vec{A}(Q) = \vec{A}(P).)
Das ist alles. Die Aufabe erwähnt zwar noch Koordinaten von P und Q sowie von 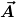 , aber die haben mit der Frage der Parallelverschiebung eigentlich gar nichts zu tun. Was die Aufgabe nicht erwähnt ist, entlang welcher Kurve wir verschieben sollen, was potentiell wichtig wäre. Aber da spezifiziert ist, daß wir uns im Euklidischen Raum befinden und mittels "Lineal und Dreieck" verschieben sollen, spielt das ebenfalls keine Rolle; die Bedingung , aber die haben mit der Frage der Parallelverschiebung eigentlich gar nichts zu tun. Was die Aufgabe nicht erwähnt ist, entlang welcher Kurve wir verschieben sollen, was potentiell wichtig wäre. Aber da spezifiziert ist, daß wir uns im Euklidischen Raum befinden und mittels "Lineal und Dreieck" verschieben sollen, spielt das ebenfalls keine Rolle; die Bedingung  = \vec{A}(P)) gilt im Euklidischen Raum unabhängig von der Kurve, die P und Q verbindet. gilt im Euklidischen Raum unabhängig von der Kurve, die P und Q verbindet.
Obwohl diese Antwort richtig ist, ist sie wohl nicht im Sinne des Aufgabenstellers. Warum erwähnt die Aufgabe nun eigentlich irgendwelche Koordinaten? Das liegt an der Art wie das Skript den Begriff kovariante Ableitung einführt. Machen wir uns den Zusammenhang nochmal klar. Auf Grund der trivialen Parallelverschiebung gilt für die kovariante Ableitung
|_{t=0} = D_{\overrightarrow{PQ}}\vec{A}(P)\qquad\text{(KA')})
Die Aufgabe spezifiziert noch  , also folgt weiter (Linearität der Richtungsableitung!) , also folgt weiter (Linearität der Richtungsableitung!)
 = \delta p D_{\vec{e}_p}\vec{A}(P) + \delta q D_{\vec{e}_p}\vec{A}(P)\qquad\text{(1)})
Hier setzt das Skript an. Wie du meinem letzten Beitrag entnehmen kannst, impliziert es die Definition
 = \left(A^i_{,p} + \Gamma^i_{np}A^n\right)\vec{e}_i \qquad\text{(Skript)})
etc. Die Christoffelsymbole fallen hier mehr oder weniger vom Himmel (für ihre eigentliche Bedeutung siehe meine früheren Antworten). Jedenfalls kommen sie gar nicht vor, wenn wir keine Basiszerlegung des Vektors vornehmen. Die Basis wird im Skript nicht explizit erwähnt. Aber von ihr hängen die Christoffelsymbole natürlich ab.
Bei Parallelverschiebung entlang der Geraden PQ gilt nun also

Fassen wir hier mit Hilfe von (Skript) alle Koeffizienten des i-ten Basisvektors auf der rechten Seite von (1) zusammen, erhalten wir für die i-te Komponente der Ableitung

Also wissen wir schon mal aus ganz allgemeinen Überlegungen

Dies gilt noch ganz allgemein und hat nichts mit "Lineal und Dreieck" oder Euklidischen Räumen zu tun. Denn wir haben noch nicht die linke Seite von (KA') benutzt, nur die allgemeine Definition (Skript) und die Linearität der Ableitung. Letztere gilt auch für die abstrakte kovariante Ableitung auf beliebigen Mannigfaltigkeiten, auch wenn das Skript darüber nichts sagt. (Wie gesagt, es definiert nicht, was die kovariante Ableitung eigentlich ist.) Aus (KA') folgt nun aber ebenso
 = 0)
Um den Zusammenhang zu (Skript) herzustellen, schreiben wir nun ) = A^i(c(t))\vec{e}_i(c(t))) mit mit  = P+t\overrightarrow{PQ}) . Wir lassen explizit zu, daß sich die Basisvektoren entlang c(t) ändern. Mit der "normalen" vektoriellen Ableitung (=kovariante Ableitung im Euklidischen Raum) erhalten wir also sofort . Wir lassen explizit zu, daß sich die Basisvektoren entlang c(t) ändern. Mit der "normalen" vektoriellen Ableitung (=kovariante Ableitung im Euklidischen Raum) erhalten wir also sofort
 = \dot{A}^i \vec{e}_i + A^i \underbrace{\frac{\dd }{\dd t}\vec{e}_i}_{=D_{\dot c}\vec{e}_i}\qquad\text{(2)})
Jetzt analysieren wir die Terme auf der rechten Seite. Der erste mit  ist einfach. Ausführlich lautet er ist einfach. Ausführlich lautet er
) = (A^i_{,q}\delta q + A^i_{,p}\delta p)\vec{e}_i)
Das ist derselbe Term, den wir mit der Definition (Skript) aus Gl. (1) erhalten. Die Christoffelsymbole müssen also aus dem zweiten Term  kommen. Dieser lautet nun ausführlich kommen. Dieser lautet nun ausführlich

Wenn man (Skript) in die rechte Seite einsetzt, ergibt sich aber
\vec{e}_i\equiv -\delta A^i \vec{e}_i.)
Nun haben wir aber eine Basis gegeben, die konstant ist im gewöhnlichen Sinne. Es gilt also  . Damit ist sie nach (KA) auch kovariant konstant im Sinne der Parallelverschiebung mit Lineal und Dreieck, d.h. . Damit ist sie nach (KA) auch kovariant konstant im Sinne der Parallelverschiebung mit Lineal und Dreieck, d.h.  . Daraus folgt sofort . Daraus folgt sofort  und deshalb mit der bereits abgeleiteten Beziehung und deshalb mit der bereits abgeleiteten Beziehung

Die dazu äquivalente Bedingung für beliebige Kurven folgt aus (2)

Beides ist eine Folgerung daraus, daß die Christoffelsymbole verschwinden, was wiederum daraus folgt, daß die Basiselemente (kovariant) konstant sind.
| Zitat: |
Wie du bereits gezeigt hast, geht all das auch ohne diesen komischen Weg (Aber was genau ist dabei nochmal das springende Argument - dass die zeitliche Ableitung von  null ist, wie in deinem Beitrag vom 18. März (14:13)?) null ist, wie in deinem Beitrag vom 18. März (14:13)?)
|
Sorry, wegen der länglichen Antwort. Aber ich hoffe dieser Punkt ist daraus nun nochmal klarer geworden.
|
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 21. März 2021 16:50 Titel: manuel459 Verfasst am: 21. März 2021 16:50 Titel: |
 |
|
Ein Weg wäre, wie du vorhin gesagt hast, ja dieser oder:
Zuerst (totales Differential) schreiben:
 . Rechnet man das aus bekommt man offensichtlich 0 heraus, da die partiellen Ableitungen 0 sind (es ist ja . Rechnet man das aus bekommt man offensichtlich 0 heraus, da die partiellen Ableitungen 0 sind (es ist ja und die partielle Ableitung von der Summe von Konstanten klarerweise 0). Analog für und die partielle Ableitung von der Summe von Konstanten klarerweise 0). Analog für  . Also sind . Also sind  . .
Verwenden wir nun, dass wegen parallelverschiebung die kovariante Ableitung 0 ist, erhalten wir, dass die Christoffelsymbole 0 sind. Diesen letzten Schritt hätten wir aber auch über Gleichung 1 aus dem Skript machen können, aber nur, wenn die  sind (was hier der Fall ist). sind (was hier der Fall ist).
Dann wäre hier nur noch komisch, weshalb der Vergleich mit Gleichung 1 notwendig ist.
PS: An einer Reaktion zum letzten Beitrag arbeite ich noch.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 21. März 2021 18:03 Titel: index_razor Verfasst am: 21. März 2021 18:03 Titel: |
 |
|
Mein Argument ginge, in relativer Kürze und maximaler Anlehnung an das Skript, so: Die i-te Komponente der kovarianten Ableitung ist ^i = \dd A^i -\delta A^i) mit mit

und

wie Gl. (1) im Skript. (Hier unbedingt zwischen  und und  unterscheiden.) unterscheiden.)
Parallelverschiebung heißt ^i = 0) entlang einer Kurve entlang einer Kurve ) also also
\dot x^k = \dot{A}^i + \Gamma^i_{nk}A^n\dot{x}^k = 0)
Parallelverschiebung liefert also in einem gegebenen Koordinatensystem 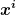 mit zugehörigen Christoffelsymbolen für eine Kurve und einen Vektor mit zugehörigen Christoffelsymbolen für eine Kurve und einen Vektor ) eine gewöhnliche Differentialgleichung für die Vektorkomponenten eine gewöhnliche Differentialgleichung für die Vektorkomponenten ) entlang der Kurve. Die Frage ist also nun, wie lösen wir das Anfangswertproblem entlang der Kurve. Die Frage ist also nun, wie lösen wir das Anfangswertproblem
 = A^i\ \text{?})
Du scheinst auf dem Standpunkt zu stehen, daß

weil  . Das ist in diesem Fall auch durchaus korrekt. Aber woraus schließt du das? Die Bedingung . Das ist in diesem Fall auch durchaus korrekt. Aber woraus schließt du das? Die Bedingung  für einen beliebigen Vektor entlang einer beliebigen Kurve ist doch absolut äquivalent zu für einen beliebigen Vektor entlang einer beliebigen Kurve ist doch absolut äquivalent zu  für alle i,k,n. für alle i,k,n.
Und dies bedeutet nichts anderes, als daß sehr spezielle Koordinaten gewählt wurden. Nämlich solche, in denen Parallelverschiebung dadurch realisiert werden kann, daß man einfach alle Vektorkomponenten entlang der Kurve konstant hält. Damit bleibt für mich die Grundfrage: woraus folgt diese Eigenschaft der gewählten Koordinaten? Woraus folgt überhaupt, daß es solche Koordinaten gibt?
Meine Antwort darauf ist, daß wir es hier schlicht und einfach mit einem Euklidischen Raum zu tun haben, in dem wir eine triviale Vorschrift zur Parallelverschiebung gegeben haben. Die Bedingung

ist die charakteristische Eigenschaft von kartesischen*) Koordinaten, realisiert durch Geraden als Koordinatenlinien und konstante Basisvektoren. Kartesische Koordinaten haben deshalb genau die beschriebene Eigenschaft

Aber das gilt, selbst im Euklidischen Raum, eben auch nur für kartesische Koordinaten.
____
*) Das stimmt nicht ganz. Eigentlich sind es nur affine Koordinaten. Kartesische Koordinaten haben außerdem orthogonale Achsen. Diese Eigenschaft spielt hier aber keine Rolle.
|
|
 |
|
|

















