| Autor |
Nachricht |
Vogelpfeife
Gast
|
 Vogelpfeife Verfasst am: 06. Nov 2019 22:17 Titel: Elektrostatisches Potential |
 |
|
Meine Frage:
In der Aufgabe sollte man zunächst die Ladungsdichte einer infinitesimal dünnen Kreisscheibe in der xy-Ebene angeben. Das habe ich getan:
=\frac{Q}{\pi R^{2}}\Theta (R-r)\delta (z))
Dann sollte man das elektrostatische Potenzial der Scheibe an einem beliebigen Punkt  ) auf der Scheibenachse bestimmen und zwar mit der Formel:
=\frac{1}{4\pi \epsilon_{0}}\int{d^{3}\vec{x'}\frac{\rho (\vec{x'})}{|\vec{x} -\vec{x'}|}} )
Auch das habe ich gemacht und bekam folgendes Ergebnis:
=\frac{Q}{2\pi \epsilon_{0}R^{2}}(\sqrt{R^{2}+z^{2}}-|z|))
Für große z entspricht das genähert dem Feld einer Punktladung.
Probleme habe ich bei Folgendem: Ich soll zeigen, dass das Potenzial am Scheibenrand den Wert annimmt:
=\frac{1}{4\pi \epsilon_{0}}\frac{4Q}{\pi R})
Ein Tipp sagt, man soll die z'-Achse dafür durch einen Punkt am Scheibenrand legen. Mir ist jedoch nicht klar, wie ich die Kreisscheibe in meinem Koordinatensystem darstellen kann, wenn das zentrum nicht der Ursprung ist. Kann mir hier jemand weiterhelfen?
Meine Ideen:
Ich hab es bereits mit verschiedenen Integrationsgrenzen probiert, jedoch ohne Erfolg. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5888
|
| Myon Verfasst am: 07. Nov 2019 11:24 Titel: |
|
|
Hab‘s zuerst ohne den Tipp versucht, weil ich dachte, das müsse auf dasselbe rauskommen, doch das führt auf ein sehr unschönes Integral. Mit dem Tipp geht es aber wider Erwarten relativ einfach.
Setzt man den Ursprung des Koordinatensystems auf einen Punkt am Rand der Scheibe, wird die Integrationsgrenze von  natürlich abhängig von 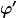 . Mangels anderer Buchstaben nenne ich die Grenze ) . Dann gilt für das Potential im Ursprung
=\frac{\sigma_0}{4\pi\varepsilon_0}\int_0^{2\pi}d\varphi'\int_0^{c(\varphi')}d\rho'\,\rho'\frac{1}{\rho'})
Die Integrationsgrenze ergibt sich, wenn man Punkte auf dem Scheibenrand betrachtet. Für diese gilt die Gleichung
^2=R^2) |
|
|
Vogelpfeife
Gast
|
| Vogelpfeife Verfasst am: 09. Nov 2019 18:20 Titel: |
|
|
Danke, ich habe jetzt nur ein Problem: wenn ich deine Gleichung nach c auflöse, erhalte ich ) und wenn ich das über phi' integriere, erhalte ich logischerweise 0, es müsste also ein sin anstelle eines kosinus dort stehen. |
|
|
Vogelpfeife
Gast
|
| Vogelpfeife Verfasst am: 09. Nov 2019 19:09 Titel: |
|
|
|
Oder darf ich dann nur von -Pi/2 bis Pi/2 integrieren, weil c für alle andern phi 0 ist? |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5888
|
| Myon Verfasst am: 09. Nov 2019 22:27 Titel: |
|
|
|
Ja, Du hast recht, die obigen Integrationsgrenzen sind falsch, sorry. Die Integration läuft von -pi/2 bis pi/2, denn wenn der Ursprung links auf dem Scheibenrand liegt (das ist bei der Gleichung für c angenommen, wobei man natürlich auch eine andere Wahl treffen kann), so muss vom Ursprung gesehen nur über die rechte Hälfte integriert werden. |
|
|
Vogelpfeife
Gast
|
| Vogelpfeife Verfasst am: 10. Nov 2019 15:46 Titel: |
|
|
Ich habe leider noch eine Frage zu der Aufgabe. Und zwar soll ich nach dem was ich jetzt gemacht habe, mit Hilfe des Ergebnisses für das Potential am Rand der Kreisscheibe noch die elektrostatische Energie der Scheibe berechnen. Als Formel für kontinuierliche Ladungsdichten (welche hier ja vorliegt) habe ich:
\rho(\vec{x'})}{|\vec{x}-\vec{x'}|}=\frac{1}{2} \int_{}^{}d^{3}x\rho(x)\phi(\vec{x}) )
Ich bin mir jetzt nicht wirklich sicher, was ich für das Potetnial einsetze in das Integral. Setze ich da dann nur das Randpotential ein? |
|
|
Vogelpfeife
Gast
|
| Vogelpfeife Verfasst am: 10. Nov 2019 15:51 Titel: |
|
|
|
Hab das Grad probiert, da kommt beinahe das richtige Ergebnis raus, allerdings mit dem Faktor 1/2 anstatt des Faktors 2/3 der richtig sein sollte, also muss es doch irgendwie anders gehen. |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5888
|
| Myon Verfasst am: 10. Nov 2019 22:50 Titel: |
|
|
Wie hast Du denn das mit der obigen Gleichung für W gerechnet, das Potential ist ja nur am Rand bekannt - hier müsste aber über die gesamte Scheibenfläche integriert werden.
Ich würde es so probieren: geh vom bekannten Potential am Rand einer Scheibe mit Radius r und Ladung  aus. Welche Arbeit dW muss man dann verrichten, wenn ein dünner Ring mit Ladung
am Scheibenrand hinzugefügt wird? Das kann man bis R aufintegrieren, dann ergibt sich auch ein Faktor 2/3. |
|
|
Vogelpfeife
Gast
|
| Vogelpfeife Verfasst am: 10. Nov 2019 23:11 Titel: |
|
|
|
Vielen Dank, der Ausdruck für die Ladung hat mein Problem gelöst. |
|
|
TheDribbler
Gast
|
| TheDribbler Verfasst am: 19. März 2023 15:27 Titel: Für große z entspricht das genähert... |
|
|
"Für große z entspricht das genähert dem Feld einer Punktladung."
Wie genau konkret zeigt man das mit einer Taylor-Entwicklung? |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5888
|
| Myon Verfasst am: 19. März 2023 16:24 Titel: |
|
|
Das Potential auf der z-Achse (Scheibenachse) ist
=\frac{Q}{2\pi\varepsilon_0R^2}(\sqrt{z^2+R^2}-|z|))
Für z>>R gilt dann
=\frac{Q|z|}{2\pi\varepsilon_0 R^2}\left(\sqrt{1+\frac{R^2}{z^2}}-1\right)\approx \frac{Q|z|}{2\pi\varepsilon_0 R^2}(1+\frac{R^2}{2z^2}-1)=\frac{Q}{4\pi\varepsilon_0|z|}) |
|
|
|
Registrieren
Login
FAQ
Suchen
