| Autor |
Nachricht |
NachtEule2
Gast
|
 NachtEule2 Verfasst am: 24. Feb 2019 03:33 Titel: Potential von Linienladung |
 |
|
Meine Aufgabe:
Eine konstante Linienladung T befindet sich auf der z-Achseim Bereich von -a bis +a mit a>0. Berechnen Sie das elektrostatische Potential phi (0,0,z) an der Position z>a auf der z-achse.
Meine Lösung aus der Übung phi(0,0,z)=T/2pi*e*ln(r/r0)
mit e=relative Permittivität
Jetzt gilt für r=z+a und r0=z-a. Ich weiß nicht so recht wie man darauf kommt. Ist auch die einzige Aufgabe die ich hierzu habe.
Wirken tut das Potential ja im Punkt r0 und das soll die z-Achse sein. Ortsvektor ist r0=(0,0,z) Betrag ist z.
Wie beschreibt man jetzt den Ortsvektor von -a bis + a?
Es handelt sich ja um eine ,,Gerade" auf der z-Achse. Aber wie man jetzt auf die Lösung komt ist mir nicht klar.
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Feb 2019 12:25 Titel: |
|
|
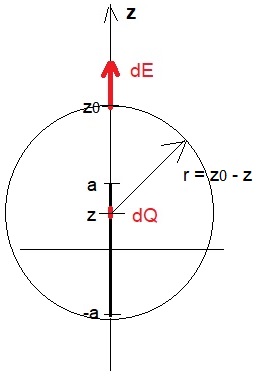
Stell Dir die Linienladung zerstückelt in differentiell kleine Abschnitte mit der Ladung dQ vor. Der Abstand einer punktförmigen Ladung dQ an der Stelle z (mit -a <= z <=+a) hat vom Punkt z0 die Abstand z0-z. Der differentiell kleine Feldstärkeanteil dieser Ladung dQ in z_Richtung ist somit
^2})
Die gesamte Feldstärke im Punkt (0,0,z0) ist die Summe (=Integral) aller Einzelfeldstärken dE.
|
|
|
Nachteule2
Gast
|
| Nachteule2 Verfasst am: 24. Feb 2019 15:43 Titel: |
|
|
Mich würde interessieren qi2e ich aus den gegebenen Informationen die Ortsvektoren r und r0 bestimmen kann wobei r im punkt r0 wirkt (Bzgl. dem Term r0-r).
Deinem Beispiel kann ich noch folgen, da gilt ja einfach nur r0=(0,0,z0) und r=(0,0,z).
Daraua folgt Betrag von r0-r.
Aber mir hilft das irgendwie nicht die Ortsvektoren meiner Aufgabe zu bestimmen..
|
|
|
NachtEule3
Gast
|
| NachtEule3 Verfasst am: 24. Feb 2019 16:58 Titel: |
|
|
Ich glaube ich hab es. Das ist ja wieder so eine typische Aufgabe die man mindestens einmal gerechnet haben muss um darauf zu kommen.
Ich denke man zeichnet einfach ein Koordinatensystem nur mit der z-Achse aufgetragen. Jetzt mal ganz provisorisch gesehen. Die Achse breitet sich nach oben ins unendliche aus. Also musst dir eine Koordinatenachse z daneben vorstellen
z
+a
0
-a
Jetzt einmal z-(+a) und z-(-a) berechnen
Ist das richtig? Das sind ja die Abstände ,d.h. differenzen der z Achse im unendlichen minus den betrachteten Punkten.
Scheint das richtig zu sein? Ist aber immer noch etwas schwer nachzuvollziehen.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Feb 2019 17:10 Titel: |
|
|
| Nachteule2 hat Folgendes geschrieben: | Deinem Beispiel kann ich noch folgen, da gilt ja einfach nur r0=(0,0,z0) und r=(0,0,z).
Daraua folgt Betrag von r0-r.
Aber mir hilft das irgendwie nicht die Ortsvektoren meiner Aufgabe zu bestimmen.. |
Ich verstehe nicht so recht, was Du meinst. Die Ortsvektoren stehen doch schon da.
Aber wozu brauchst Du die?
|
|
|
Nachteule3
Gast
|
| Nachteule3 Verfasst am: 24. Feb 2019 17:14 Titel: |
|
|
|
Naja, ich wollte von den Ortsvektoren auf die Beträge r und r0 schließen das funktioniert aber hier glaube ich nicht denn dann würde z/z0 im ln() stehen ...
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Feb 2019 17:19 Titel: |
|
|
| Nachteule3 hat Folgendes geschrieben: | | Naja, ich wollte von den Ortsvektoren auf die Beträge r und r0 schließen das funktioniert aber hier glaube ich nicht denn dann würde z/z0 im ln() stehen ... |
Irgendwie bist Du noch auf dem falschen Dampfer. An welcher Stelle kommt denn der natürliche Logarithmus vor?
|
|
|
Nachteukle3
Gast
|
| Nachteukle3 Verfasst am: 24. Feb 2019 17:21 Titel: |
|
|
Das Potential einer Linienladung T am Punkt r0 lautet
phi(r0)=T/(2*pi*permittivität)*ln(r/r0)
Jetzt muss ich r und r0 bestimmen.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Feb 2019 17:36 Titel: |
|
|
| Nachteukle3 hat Folgendes geschrieben: | Das Potential einer Linienladung T am Punkt r0 lautet
phi(r0)=T/(2*pi*permittivität)*ln(r/r0)
Jetzt muss ich r und r0 bestimmen. |
Moment, so weit sind wir noch nicht. Wir sind, wenn ich das richtig sehe, noch bei der Bestimmung der Feldstärke an einem bestimmten Punkt auf der z-Achse, den ich erstmal z0 genannt habe (weil ich z als Variable in den Grenzen von -a bis +a verwenden will).
|
|
|
Nachteule3
Gast
|
| Nachteule3 Verfasst am: 24. Feb 2019 18:04 Titel: |
|
|
Ach sooo, ok gut das du das erwähnt hast. Eine Herleitung ist definitiv notwendig. Also zunächst bestimmen wir die Feldstärke einer Linienladungsdichte T.
Es gilt SSDA=Q mit T=Q/l <-> Q=T*L
Es folgt SS DA=Q=T*L. Mit A der Mantelfäche eines Zylinders A=2pirL.
folgt D=TL/(2piRL)=T/(2piR) mit E=D/e=T/(2*pi*R*Oermittivität) bzw Vector E=E*Basisvektor e_zv
Ich glaube bei diesem r handelt es sich jedoch um keinen radius sondern um einen abstand oder? Der wird dann umgeschrieben zu z0-z
Das jetzt integrieren von -a bis +a mithilfe S Edz=Potential(a)-Potential(-a).
hmm das entspricht aber einer Spannung und keinem Potential ...
Nach dem integrieren wird man sicherlich noch ln(a)-ln(b)=ln(a/b) anwenden müssen, dann sollte das so inetwa passen mit der gesuchten allgemeinen Formel. Aber wenn ich jetzt meine Feldstärke integriere habe ich keine z Abhängigkeit und diese sollte vorhanden sein
Du hast mich aufjedenfall in die Richtige Richtung gelenkt, dennoch habe ich Probleme damit wieso man den Radius R jetzt umschreibt als den Abstand zwischen r0-r. Also in diesem Fall z0-z
Mir ist bewusst das die Feldstärke im Punkt r im Punkt r0 wirkt. Aber mir macht es irgendwie Probleme diesen Unterschied zwischen Abstand und Radius zu erkennen.
Oder man kann glaube ich R=/r0-r/ umschreiben und jetzt setzen wir unsere Ortsvedktoren ein.
Geht das so ?
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
|
|
Nachteule3
Gast
|
| Nachteule3 Verfasst am: 24. Feb 2019 20:46 Titel: |
|
|
Wenn ich das so mache wie du sagst, dann habe ich eine Funktion von 4*pi aber das Potential bzw das E-Feld der Linienladungsdichte ist eine Funktion von 2*pi (Wie kommt man dann auf die 2*pi wenn nicht ein Zylindermantel betrachtet wird) ..
Also ich kann dir schon folgen, bloß ich habe im Falle einer Linienladung immer einen Zylinder betrachtet und nicht eine Kugel.,
|
|
|
nachteule3
Gast
|
| nachteule3 Verfasst am: 24. Feb 2019 21:03 Titel: |
|
|
|
moment ich glaube du hast recht. Aber ich kann schwören ich habe in einem anderen Beitrag gelesen das man einfach den Mantel eines Zylinders betrachtet.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Feb 2019 21:53 Titel: |
|
|
| nachteule3 hat Folgendes geschrieben: | | moment ich glaube du hast recht. Aber ich kann schwören ich habe in einem anderen Beitrag gelesen das man einfach den Mantel eines Zylinders betrachtet. |
Ja, wenn Du die Feldstärke in einem radialen Abstand von der Linienladung bestimmen willst. Das ist hier aber nicht der Fall. Ich fürchte, Du hast den Gaußschen Flusssatz noch nicht wirklich verstanden.
|
|
|
Nachteukle3
Gast
|
| Nachteukle3 Verfasst am: 24. Feb 2019 22:04 Titel: |
|
|
So, ich hab mir jetzt einige Gedanken dazu gemacht und laut recherchen ist es so dass man den Satz von Gauß bzgl eines Zylinders im Falle einer Linienladung nur machen darf, wenn die Ladungsdichte invariant ist, dh sie muss sich unendlich ausbreiten. Dadurch geht der Radius gegen unendlich.
Im falle einer endlichen Ausdehnung wie hier muss man anders vorgehen. Wenn ich jetzt dein Integral dE einsetze in E=SdE folgt nachdem man alle konstanten rauszieht SdQ von -a bi +a und das ergibt
E=1/((4pi*e)*(z-z0)^2)
Danke sehr!
Ich hätte mal jetzt eine Frage bzgl der berechnen eines Potentials (nicht Spannung). Es gilt ja U=phi(r2)-phi(r1)=S Eds von r1 bis 2 allgemein.
Wie berechnet man jetzt aber nur phi(r2) bzw phi(r1). Man muss die Integrale glaube ich umschreiben zu SEds von r1 bis r2 zu
SEds von -00 bis r1 + r2 bis unendlich ? Oder so ähnlich vermute ich mal ..
Also es geht darum wie man Potentiale anstatt Spannungen berechnet.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Feb 2019 22:56 Titel: |
|
|
| Nachteukle3 hat Folgendes geschrieben: | | ... dass man den Satz von Gauß bzgl eines Zylinders im Falle einer Linienladung nur machen darf, wenn die Ladungsdichte invariant ist, dh sie muss sich unendlich ausbreiten. Dadurch geht der Radius gegen unendlich. |
Da verstehst Du was falsch. Der Radius, also der senkrechte Abstand von der Linienladung hat nichts mit der Ausdehnung der Linienladung zu tun. Tatsächlich ist mit dem, was Du gelesen (recherchiert), aber offenbar nicht verstanden hast, gemeint, dass nur bei unendlicher Ausdehnung der Linienladung die Feldstärke in einem radialen Abstand einfach per Gaußschem Flusssatz bestimmt werden kann. Grund dafür ist der nur bei unendlicher Linienladung symmetrische Verschiebungsdichteverlauf, der auf der Oberfläche eines koaxialen Zylinders wegen des konstanten Abstandes einen konstanten Verschiebungsdichtebetrag bewirkt. Mit dem Potential ist es schon schwieriger, weil im zylindersymmetrischen Feld das Potential im Unendlichen nicht null wird.
Mit der vorliegenden Aufgabe hat das alles aber nichts zu tun. Hier ist weder die Linienladung unendlich ausgedehnt noch ist die Feldstärke in radialem Abstand gefragt, somdern in einem Punkt in Verlängerung der Linienladung. Ich verweise in diesem Zusammenhang nochmal auf die Skizze in meinem vorletzten Beitrag.
| Nachteukle3 hat Folgendes geschrieben: | ... und das ergibt
E=1/((4pi*e)*(z-z0)^2) |
Das ist nicht richtig. Hier fehlt die differentiell kleine Ladung dQ=T*dz im Zähler. Selbst wenn Du die einsetzt, ergibt das nicht die Feldstärke E, sondern den differentiell kleinen Feldstärkeanteil infolger der Punktladung dQ (an der Stelle z), ergibt also dE. Um die gesamte Feldstärke an der Stelle z0 zu erhalten, musst Du die Feldstärkeanteile aller Punktladungen dQ von -a bis +a aufsummieren, d.h. integrieren. Aber das habe ich Dir schon in meinem ersten Beitrag gesagt. Nun mach das doch erstmal. Danach können wir an die Bestimmung des Potentials gehen. Ohne Kenntnis des Feldstärkeverlaufs ist das nicht möglich.
|
|
|
Nachteule3
Gast
|
| Nachteule3 Verfasst am: 24. Feb 2019 23:24 Titel: |
|
|
Ja, da hast du recht. War wohl zu früh gefreut.
Es folgt mit dQ=T*dz
SEdz von -a bis a
E=-T/(4pi*e)(-1/(z0-a) + 1/(z0+a))
Sieht nicht sehr schön aus ?
|
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 24. Feb 2019 23:43 Titel: |
|
|
Nur zur Form, nicht zur Sache:
| Nachteule3 hat Folgendes geschrieben: | | Sieht nicht sehr schön aus ? |
So ist es. Im Land der Physik verständigt man sich, wie von GvC demonstriert, in einer (Formel-) Sprache, geschrieben zum Beispiel mit LaTeX: Kleine Mühe, großer Nutzen.
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
| Myon Verfasst am: 25. Feb 2019 00:24 Titel: |
|
|
Ich verstehe nicht ganz, wieso zuerst das E-Feld bestimmt wird, wo doch nach dem Potential gefragt wird. Man kann vom Potential eines Elements der Länge dz' bei z' ausgehen,
)=\frac{T\,dz'}{4\pi\varepsilon_0(z-z')})
(wobei nach Voraussetzung z>a und T=Q/(2a) die Linienladungsdichte ist) und dann integrieren. Die im ersten Beitrag erwähnte Lösung ist wahrscheinlich um einen Faktor 2 zu gross.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 25. Feb 2019 12:44 Titel: |
|
|
| Myon hat Folgendes geschrieben: | | Ich verstehe nicht ganz, wieso zuerst das E-Feld bestimmt wird, wo doch nach dem Potential gefragt wird. |
Ja, da hast Du allerdings recht. Da habe ich ein bisschen zu kompliziert gedacht. Das liegt daran, dass ich die Aufgabenstellung zunächst nicht sorgfältig genug gelesen hatte und deshalb davon ausgegangen war, dass die Feldstärke und nicht das Potential auf der z-Achse gesucht sei. Ich entschuldige mich hiermit bei dem Fragesteller, dass ich die Lösungsstrategie unnötig verkompliziert habe.
| Myon hat Folgendes geschrieben: | | Die im ersten Beitrag erwähnte Lösung ist wahrscheinlich um einen Faktor 2 zu gross. |
Nein, das ist nicht der Fall.
Im Nachhinein erscheint es mir allerdings wichtig, noch einmal auf das Missverständnis des Fragestellers bzgl. des Gaußschen Flusssatzes hinzuweisen, d.h. dass es sich bei der Hüllfläche im Gaußschen Satz hier nicht um eine Zylindermantelfläche, sondern um eine Kugeloberfläche handelt.
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
| Myon Verfasst am: 25. Feb 2019 15:10 Titel: |
|
|
Hmm.. wenn man integriert, erhält man doch
)=\frac{T}{4\pi\varepsilon_0}\ln\left(\frac{z+a}{z-a}\right))
(?) Wo kommt denn der Faktor 2 her?
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 25. Feb 2019 15:21 Titel: |
|
|
| Myon hat Folgendes geschrieben: | Hmm.. wenn man integriert, erhält man doch
(?) Wo kommt denn der Faktor 2 her? |
Ich verstehe nicht, was Du meinst. Das kommt doch in beiden Fällen raus. Oder nicht?
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
| Myon Verfasst am: 27. Feb 2019 10:54 Titel: Re: Potential von Linienladung |
|
|
Ich meinte nicht die Rechnung über das E-Feld, sondern die vom Fragesteller angegebene „Lösung“
| NachtEule2 hat Folgendes geschrieben: | Meine Lösung aus der Übung phi(0,0,z)=T/2pi*e*ln(r/r0)
mit e=relative Permittivität
Jetzt gilt für r=z+a und r0=z-a... |
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 27. Feb 2019 12:56 Titel: Re: Potential von Linienladung |
|
|
| Myon hat Folgendes geschrieben: | Ich meinte nicht die Rechnung über das E-Feld, sondern die vom Fragesteller angegebene „Lösung“
| NachtEule2 hat Folgendes geschrieben: | Meine Lösung aus der Übung phi(0,0,z)=T/2pi*e*ln(r/r0)
mit e=relative Permittivität
Jetzt gilt für r=z+a und r0=z-a... |
|
Da hat er/sie noch das Potential eines Punktes in radialem Abstand von der Linienladung bestimmen wollen. Selbst wenn danach gefragt gewesen wäre, wäre die Lösung falsch gewesen, da sie nur für eine unendlich ausgedehnte Linienladung gilt.
Mit der hier vorliegenden Aufgabe hat das alles nichts zu tun.
|
|
|
|
Registrieren
Login
FAQ
Suchen
