| Autor |
Nachricht |
Felix (Gast)
Gast
|
 Felix (Gast) Verfasst am: 12. Mai 2006 16:24 Titel: Atomphysik: Zerfall von Uran Felix (Gast) Verfasst am: 12. Mai 2006 16:24 Titel: Atomphysik: Zerfall von Uran |
 |
|
Hallo, ich habe da ein Problem mit einer Aufgabe die ich für nächste Woche als Hausaufgabe habe. Wäre echt super wenn mir da jemand helfen könnte.
Sie lautet: Berechnen Sie, wieviel %  nach einer Million Jahren zerfallen sind. nach einer Million Jahren zerfallen sind.
[hab' mal latex daraus gemacht, para]
[Titel ergänzt, dermarkus] |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
|
 |
kruemel
Anmeldungsdatum: 10.07.2006
Beiträge: 6
|
 kruemel Verfasst am: 11. Jul 2006 14:57 Titel: kruemel Verfasst am: 11. Jul 2006 14:57 Titel: |
 |
|
Hallo zusammen,
sitze seit gestern an der gleichen Aufgabe und blicke mit dieser dämlichen Formel einfach nicht durch 
die Halbwertszeit ist laut meinen Unterlagen 0,71*10^9 Jahre
und ich soll angeben was nach 1 Mio Jahre zerfallen ist soweit so sch...
jetzt habe ich die Formel:
N = No * e^λt
N = Anzahl der vorhandenen Atomkerne zum Zeitpunkt t ? und wann ist der?
No = Anzahl der vorhandenen Atomkerne zum Zeitpunkt t = 0 ? weis ich auch nicht wann das sein soll
e = Euler'sche Zahl = 2,718281828459...
λ = ?
kann mir jemand vernünftig erklären wie man mit dieser Formel rechnet und welche Werte man wo zu verwenden hat?
Ich bin euch jetzt schon mehr als dankbar für jede Erklärung, ich raffs echt nicht... vielleicht verhelft ihr mir zur Erleuchtung
lg
kruemel |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 11. Jul 2006 15:16 Titel: Nikolas Verfasst am: 11. Jul 2006 15:16 Titel: |
 |
|
Das t_0 darfst du setzen, wann du willst. t beschreibt dann die Zeit nach diesem Zeitpunkt. Da Lambda nicht von der urspünglichen Masse abhängt, ist diese Wahl von t_0 unwichtig. Ist ja auch anschaulich klar: ob ich jetzt eine Zerfallsdauer der Atome messe, oder jemand anders vor ein paar Millionen Jahren, sollte nichts an der Zerfallsgeschwindigkeit der Atome ändern.
An das Lambda ranzukommen ist auch nicht unmöglich:
Nach Ablauf einer Halbwertszeit ist die Hälfte der Atomkerne zerfallen, die beim Zeitpunkt t_0 vorhanden waren. N_0 kannst du z.B. einfach auf 100 setzen, dann beschreibt die Formel wie viel Teilchen noch nicht zerfallen sind. Die Zeit rechnest du am Besten in Jahren.
Also gilt =50=100*e^{(0,71*10^9)*\lambda})
Die Gleichung kannst du jetzt nach lambda auflösen (Stichwort Logarhytmus naturalis) und hast dein lambda. Da hier ein zerfall beschrieben ist, sollte lambda negativ sein.
Um die ursprüngliche Frage zu beantworten, muss du jetzt einfach =100*e^{10^6*\lambda}) ausrechnen. Dieser Wert entspricht dann dem Prozentsatz an Teilchen, die noch nicht zerfallen sind. ausrechnen. Dieser Wert entspricht dann dem Prozentsatz an Teilchen, die noch nicht zerfallen sind.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
kruemel
Anmeldungsdatum: 10.07.2006
Beiträge: 6
|
 kruemel Verfasst am: 11. Jul 2006 18:41 Titel: kruemel Verfasst am: 11. Jul 2006 18:41 Titel: |
 |
|
Hallo Nikolas,
danke für deine Antwort. 
| Toxman hat Folgendes geschrieben: | =50=100*e^{(0,71*10^9)*\lambda})
|
okay das hab ich jetzt kapiert, 50 da es die Hälfte von 100 ist und in der angegebenen Zeit um die Hälfte zerfällt.
aber das mit dem auflösen nach λ kann ich nicht...
liegt wahrscheinlich daran das ich logarithmen noch nie kapiert habe...
könntest du mir das Schritt für Schritt erklären, gerne auch an einem anderen Bsp. damit ich meines selbst rechnen kann?
Mein Problem bei soetwas ist das wenn ich eine vergleichbare Aufgabe schon mal gerechnet gesehen habe ich es viel einfacher verstehe als pure Theorie.
Wäre echt super nett.
| Zitat: | =100*e^{10^6*\lambda}) ausrechnen. Dieser Wert entspricht dann dem Prozentsatz an Teilchen, die noch nicht zerfallen sind. ausrechnen. Dieser Wert entspricht dann dem Prozentsatz an Teilchen, die noch nicht zerfallen sind. |
okay das kapiere ich auch soweit wie oben. Den Hintergrund habe ich jetzt verstanden, wenn du mir jetzt noch den Rest erklären könntest wäre ich dir echt dankbar.
lg
krumel |
|
 |
Crotaphytus

Anmeldungsdatum: 21.10.2005
Beiträge: 138
|
 Crotaphytus Verfasst am: 11. Jul 2006 20:01 Titel: Crotaphytus Verfasst am: 11. Jul 2006 20:01 Titel: |
 |
|
Ja, mit dem Logarithmus haben viele für den Anfang ihre liebe Not...
Was ist der Logarithmus allgemein? Er ist die Umkehrfunktion der Exponentiation. (Für die folgenden Beispiele nehm ich übrigens die Basis 10, geht schöner als mit e.)
So, jetzt klingt Umkehrfunktion ziemlich dramatisch. Ist es aber nicht, genau genommen wendest du das (fast) jeden Tag an! Einfaches Beispiel, ganz ohne Logarithmen. Du hast die Gleichung
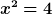
Dann ist das Ergebnis logischerweise 2 (genau genommen auch -2, aber das soll uns jetzt nicht stören). Aber was genau hast du gemacht?
In der Gleichung wird eine Funktion auf x angewandt - x wird quadriert. Wenn du jetzt x alleine haben willst, dann musst du auf beiden Seiten die Umkehrfunktion zu dieser Quadrierung anwenden. Die Umkehrfunktion, das ist die Funktion, für die gilt
) = x)
wobei 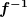 nun eben genau die Umkehrfunktion zu f sein soll. Die Umkehrfunktion in diesem Beispiel ist aber genau die Wurzelfunktion. Wenn du diese auf beiden Seiten anwendest, dann hast du (sehr umständlich geschrieben) nun eben genau die Umkehrfunktion zu f sein soll. Die Umkehrfunktion in diesem Beispiel ist aber genau die Wurzelfunktion. Wenn du diese auf beiden Seiten anwendest, dann hast du (sehr umständlich geschrieben)
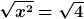
Damit folgt dann natürlich sofort x=2.
Umkehrfunktionen kannst du allgemein immer nutzen, wenn auf das x irgendeine Funktion angewandt wird, du aber x alleine brauchst. Nehmen wir nun diese Gleichung:
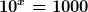
Auch hier ist das Ergebnis natürlich sofort ersichtlich. Aber wir wollen dafür mal Umkehrfunktionen einsetzen. Die Umkehrfunktion zu  ist der Logarithmus zur Basis 10. Auf beiden Seiten angewandt hast du also ist der Logarithmus zur Basis 10. Auf beiden Seiten angewandt hast du also
 = \log (1000))
Links steht jetzt per Definition ein x, rechts muss natürlich die drei rauskommen.
So... Und spätestens, wenn du die 10 durch irgendeine andere Zahl vertauschst, kannst du das nicht mehr im Kopf ausrechnen, sondern brauchst diese Umkehrfunktionen. Nehmen wir einfach mal die Zahl e als Basis. Deren Umkehrfunktion ist der natürliche Logarithmus ln. Somit musst du für deine Rechnung also den anwenden, um auf das x zu kommen.
Ich hoffe, es ist etwas klarer geworden. Ich schreib das so lang und ausführlich, weil ich das Zeug mit den Logarithmen in der Schule nie verstanden hab - wir hatten blöderweise Lehrer, die selber nicht so viel damit zu tun haben wollten, und da nicht großartig was zu erklärt haben. Hieß einfach "das ist so und so", konnt sich keiner merken, hat keiner verstanden, und das wars dann...
_________________
Genie oder Wahnsinn? Wer kann es wissen... |
|
 |
kruemel
Anmeldungsdatum: 10.07.2006
Beiträge: 6
|
 kruemel Verfasst am: 11. Jul 2006 22:34 Titel: kruemel Verfasst am: 11. Jul 2006 22:34 Titel: |
 |
|
| Crotaphytus hat Folgendes geschrieben: | | wir hatten blöderweise Lehrer, die selber nicht so viel damit zu tun haben wollten, und da nicht großartig was zu erklärt haben. Hieß einfach "das ist so und so", konnt sich keiner merken, hat keiner verstanden, und das wars dann... |
die Pappnasen kenn ich glaube ich irgendwoher!
Danke für deine Erklärung ich habe mal ausnahmsweise verstanden was ein Logarithmus ist! *freu*
Das heißt wenn ich jetzt nur e^0,71 *10^9 da stehen hätte wären das erstmal e^710000000 = 20,381
kann das hinhauen?
und wie bekomme ich das lambda da weg? |
|
 |
Crotaphytus

Anmeldungsdatum: 21.10.2005
Beiträge: 138
|
 Crotaphytus Verfasst am: 11. Jul 2006 23:03 Titel: Crotaphytus Verfasst am: 11. Jul 2006 23:03 Titel: |
 |
|
Der Gedankengang ist richtig, aufgeschrieben ists falsch: Da fehlen noch zwei Klammern!
Das Lambda ist ja genau das, was du am Ende ausrechnen willst - du kannst es gern auch x nennen, wenn das für dich leichter ist. Der erste Schritt, den du in der Aufgabe zu tun hast, ist ja das Lambda auszurechnen. Und das geht genau so, wie ich das beschrieben habe: Umkehrfunktion anwenden, um das e^ wegzukriegen, und dann weiter auflösen.
Zum besseren Verständnis vielleicht noch ein kleines Beispiel: Wie du mit Formeln der Form e^x umgehen kannst, hab ich dir ja erklärt. Was machst du jetzt mit e^2x? Genau das gleiche! Wenn du hierauf den Logarithmus anwendest, bleibt nur noch 2x stehen, das e^ fällt weg.
Wenn du das nicht nur lernen oder auch glauben willst, kannst du dir das auch gern mathematisch überlegen. Du weißt, dass ln(e^x) = x. Jetzt haben wir ln(e^2x). Wir substituieren also y := 2x. Dies ergibt ln(e^y) = y nach Definition. Die Resubstitution liefert dann y = 2x.
Das war jetzt aber wirklich sehr übertrieben, und würd keiner so machen. Aber ich hoffe, man versteht das Prinzip und was man mit Logarithmen anstellen kann.
Versuch dich jetzt einfach mal an der Aufgabe. Wenn du willst, kann ich dir dann später noch n bisschen was zum Thema Logarithmengesetze sagen, sprich Rechenregeln für Logarithmen. Die sind eigentlich sehr logisch, wenn man weiß, wo sie herkommen, aber wenn man sie nur sieht versteht man absolut nicht, warum das so sein soll... Auch das war etwas, das mir die Lehrer nicht wirklich näherbringen konnten...
_________________
Genie oder Wahnsinn? Wer kann es wissen... |
|
 |
kruemel
Anmeldungsdatum: 10.07.2006
Beiträge: 6
|
 kruemel Verfasst am: 14. Jul 2006 19:15 Titel: kruemel Verfasst am: 14. Jul 2006 19:15 Titel: |
 |
|
sorry war die letzten beiden Tage im Bettchen gelegen...
also ich glaube ich habe es jetzt kapiert
wenn
N 0,5 = N * e^710000000*λ
dann ist
ln 0,5 = 710000000 * λ
daraus folgt
λ = ln 0,5 / 710000000
λ = -0,6931472 / 710000000
λ = -9,7626* 10^-10
??? stimmt das?
und dann noch in die andere Formel einfügen?
Wenn das stimmt fress ich en Besen! |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 14. Jul 2006 19:21 Titel: as_string Verfasst am: 14. Jul 2006 19:21 Titel: |
 |
|
| kruemel hat Folgendes geschrieben: | | Wenn das stimmt fress ich en Besen! |
Na dann: Guten Appetit! 
Gruß
Marco |
|
 |
kruemel
Anmeldungsdatum: 10.07.2006
Beiträge: 6
|
 kruemel Verfasst am: 14. Jul 2006 20:57 Titel: kruemel Verfasst am: 14. Jul 2006 20:57 Titel: |
 |
|
hm schmeckt leicht trocken! 
aber vielleicht ganz gut für die Verdauung 
jetzt häng ich aber schon wieder fest... es ist doch zum Mäuse melken!!!
jetzt hab ich das in die andere Formel eingesetzt und bekomme da für N = -693,178... raus
doch wie komme ich jetzt auf die %? das andere sind ja keine 100% was ich erst errechnet habe oder... ich glaub ich hab immer noch Fieber...
könnt ihr mir nochmal helfen? DANKE DANKE DANKE |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 15. Jul 2006 11:00 Titel: Nikolas Verfasst am: 15. Jul 2006 11:00 Titel: |
 |
|
Was hast du denn wo eingesetzt? Eine Exponentialfunktion dürfte eigentlich keine negativen Funktionswerte ausgeben. Hast du die Klammern richtig gesetzt?
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
kruemel
Anmeldungsdatum: 10.07.2006
Beiträge: 6
|
 kruemel Verfasst am: 15. Jul 2006 11:54 Titel: kruemel Verfasst am: 15. Jul 2006 11:54 Titel: |
 |
|
hat sich erledigt... hatte etwas verwechselt und schon entsteht mist...

Nochmals Danke euch allen für eure konstruktive Unterstützung, ihr habt mir wirklich einiges klarer werden lassen!  |
|
 |
|





















