| Autor |
Nachricht |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 23. März 2006 12:19 Titel: dermarkus Verfasst am: 23. März 2006 12:19 Titel: |
 |
|
| Anonymous hat Folgendes geschrieben: | Der Apfel am Baum bewegt sich schneller nach
Osten, als der Boden unter ihm, denn in einem rotierenden Gebilde hängt die Bahngeschwindigkeit
eines Ortes von seinem Abstand vom Drehzentrum ab, hier der Erdmitte.
|
Das stimmt, auf einem Baum von 1 m Höhe ist der Apfel bei gleicher Winkelgeschwindigkeit um etwa 70 Mikrometer/s schneller als der Erdboden. Berechnungen mit Rotationsbewegungen im nicht mitrotierenden Bezugssystem sind aber nicht ganz ohne.
Im folgenden hat Gast vergessen, dass während des horizontalen Wurfs, von dem er spricht, die Erde sich so weiterdreht, dass die Komponente der Bewegung, die anfangs die horizontale war, anfängt, schräg zur Erdbeschleunigung zu stehen. Und zwar so, dass die Erdbeschleunigung diese anfänglich horizontale Geschwindigkeitskomponente signifikant abbremst. Wenn Gast dann keine Lust mehr haben sollte, diese komplexere Berechung im nichtmitrotierenden Bezugssystem sorgfältig durchzuziehen, dann könnte ich das sehr gut nachvollziehen. Denn ich finde die Beschreibung im mitrotierenden Bezugssystem mit der Corioliskraft viel übersichtlicher und einfacher zu rechnen.
Zuletzt bearbeitet von dermarkus am 24. März 2006 10:20, insgesamt einmal bearbeitet |
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 23. März 2006 18:39 Titel: Opa Verfasst am: 23. März 2006 18:39 Titel: |
 |
|
Nachtrag zu dermarkus:
> Einverstanden, diese Massenstücke ziehen nach oben. <
Und wenn das ganze in einem Berg stattfindet, dann wird man deshalb leichter. <
Wenn einmal erkannt ist, daß es Massenstücke gibt, die nach oben ziehen, dann reicht dies vollkommen aus. Es spielt keine Rolle, ob das ganze in einem Berg stattfindet oder woanders, solange nur es Massenstücke über dem Kopf gibt.
Das ist eine Analogie, besser noch, ein logischer Schluß. Vielen Dank, es ist schwer gewesen, ein erstes Einverständnis zu erhalten.
> Ich nehme zu Wagenscheins Gunsten an, dass er mit seinem anschaulichen Bild dies gemeint hat.
Wenn das ganze unter Meereshöhe stattfindet, dann allerdings gilt Wagenscheins einfaches anschauliches Bild nicht mehr. <
Das wäre wohl unlogisch gedacht, aus zwei Gründen.
Einmal ist es vollkommen egal, wo man sich befindet, wenn man nur zwei Massen hat, solche wie die beiden dicken schwarzen Kugeln, aus einem Physiklehrmittelraum stammende. Sie entsprechen etwa Eulers Berg und einem daneben gehaltenen Lot.
Die beiden Kugeln besitzen Zugkräfte, die beiden Massen ziehen sich an. Viele Seiten im Netz beschreiben ausgeklügelte Experimente, die das nachweisen. Der Nachweis gelingt unabhängig davon, ob man sich in einem Berg befindet oder nicht.
Und er gelingt auch unabhängig davon, ob man sich unter Meereshöhe befindet.
Zweitens denke man sich die beiden Kugeln senkrecht übereinander angeordnet, alles klar?
Wagenscheins Bild stimmt also auch hier, gewiß ist es vereinfacht, aber es stimmt.
Schließlich hält doch Jupiter seine Monde mit solchen Zugkräften, und auch die Erde hält den Mond.
O, ich sehe, der Apfel findet großes Interesse.
Tycho Brahe schreibt 1589: „... sage mir, wie kann denn eine Bleikugel, die man von einem recht hohen Turm in passender Weise fallen läßt, den genau lotrecht unter ihr liegenden Punkt der Erde treffen? Eine einfache mathematische Überlegung zeigt Dir, daß dies bei bewegter Erde vollkommen unmöglich ist. Selbst in unseren Breiten müßte sich ein Erdpunkt in einer Sekunde noch um 150 Doppelschritte nach Osten weiterdrehen.“
Kann man, nach heutigem Wissen, darauf schließen, wo auf der Erde (in welchen Breiten) Tycho Brahe sich befand, als er die Angabe 150 Doppelschritte schrieb?
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 23. März 2006 18:59 Titel: as_string Verfasst am: 23. März 2006 18:59 Titel: |
 |
|
| Opa hat Folgendes geschrieben: |
Kann man, nach heutigem Wissen, darauf schließen, wo auf der Erde (in welchen Breiten) Tycho Brahe sich befand, als er die Angabe 150 Doppelschritte schrieb? |
Wenn man wüßte, wie viel ein Doppelschritt ist... Aber dafür braucht man kein sehr aktuelles Wissen. es reicht, wenn man den Erdradius kennt und die Winkelgeschwindigkeit der Erde.
Übrigens ist die Vorstellung von Brahe total falsch, wenn ich ihn soweit richtig verstehe zumindest. Er dachte nämlich, dass der Apfel genau senkrecht fällt und sich die Erde darunter wegdreht. Er dachte nicht daran, dass der Apfel/Kugel ja auch eine Geschwindigkeit in Rotationsrichtung hat und deshalb sich auch beim freien Fall mit der Erde quasi mit dreht. Die Ablenkung durch die Corioliskraft ist da nicht so besonders groß und nur messbar, wenn man Störungen durch die Luftumströmung etc. ausschließt, also den Versuch im Vakuum durchführt. (siehe Post von dermarkus weiter oben). Die Aussage ist also weitestgehen falsch, dass es bei einer Rotation der Erde gar nicht sein könnte, dass der Apfel genau nach unten fällt, zumindest wenn man den eher kleinen Einfluß der Corioliskraft mal außer Acht läßt...
Gruß
Marco
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 23. März 2006 21:04 Titel: Opa Verfasst am: 23. März 2006 21:04 Titel: |
 |
|
Mit einem Doppelschritt dürfte er den passus gemeint haben, einige Lateinwörterbücher oder Seiten im Netz geben ca. 1,50 m dafür an. Andere legen 1 pes zu 0,296 m zugrunde und kommen dann mit 5 Füßen = 1 passus (Klafter oder Doppelschritt) auf 1,48 Meter. Wie rechnet man jetzt aus, wo sich Tycho befunden haben mag?
Gruß Opa
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 23. März 2006 22:05 Titel: dermarkus Verfasst am: 23. März 2006 22:05 Titel: |
 |
|
| Opa hat Folgendes geschrieben: | | Wie rechnet man jetzt aus, wo sich Tycho befunden haben mag? |
Brahe schreibt, in 1s dreht sich "in unseren Breiten" die Erdoberfläche um 150 Doppelschritte = ca. 150*1,50 m = 225 m weiter.
Der Abstand r von der Drehachse der Erde in der geographischen Breite, die ich hier mit dem Winkel phi bezeichne, ist
 )
Die Drehgeschwindigkeit v im Abstand r von der Drehachse bei der Winkelgeschwindigkeit omega ist
 = 462 \frac{m}{s} \cdot \cos(\varphi) )
Damit folgt für die geographische Breite phi:

Das entspräche also zum Beispiel in etwa der geographischen Breite von Oslo oder Stockholm. Das kann Sinn machen, wenn man weiß, dass Brahe Däne war und im heutigen Südschweden geboren wurde.
Zuletzt bearbeitet von dermarkus am 23. März 2006 22:48, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 23. März 2006 22:16 Titel: dermarkus Verfasst am: 23. März 2006 22:16 Titel: |
 |
|
Ich glaube, ich habe nun wieder etwas dazugelernt:
Wenn ich in meinen Bildlein 4A bis 4D die ganze Erde betrachten möchte, dann muss ich auch im Schritt von 4A nach 4B die ganze Kugelschale abziehen.
Opa hat mich aber richtig verstanden, dass ich an dieser Stelle einfach nur daran gedacht hatte, das, was ich hier von 4A nach 4B wegnehme, mit Bouguers Formel für die Massenplatte zu berechnen. (Interessanterweise gibt das übrigens genau die halbe Kraft der ganzen Kugelschale.)
Und dann darf ich natürlich im Schritt von 4C ganze Erde nach 4D ganze Erde auch nur die Massenplatte obendrüber wieder dazutun, und die zieht in der Tat nach oben,
| Opa hat Folgendes geschrieben: |
... egal, wo man sich befindet.
|
|
|
 |
Gast
|
 Gast Verfasst am: 24. März 2006 01:19 Titel: Gast Verfasst am: 24. März 2006 01:19 Titel: |
 |
|
> Rotationsbewegungen im nicht mitrotierenden Bezugssystem sind aber nicht ganz ohne.
Günstigerweise haben wir diesen Fall hier nicht, unser Bezugssystem, der Erdboden, rotiert mit, und dort messen wir ja den Versatz. Ich versuche mal eine möglichst einfache Beschreibung, eventuell ganz im Sinne von Wagenschein, ich kenne das Buch allerdings nicht. Und Hookes virtuelles Federmännchen kriegt dann auch wieder was zu tun..
Der Coriolis-Effekt ist ein Trägheitseffekt, der auf der radiusabhängigen Bahngeschwindigkeit beruht. Solche Trägheitskräfte sind Scheinkräfte in rotierenden Systemen und führen bei radialer Bewegung in Richtung Zentrum zur Ablenkung in Richtung der Rotation. Nichts anderes beschreibt auch der waagerechte Wurf nach Osten, wobei die Startgeschwindigkeit das Produkt aus der Winkelgeschwindigkeit w der Erde (siderisch wenn's sein muss) und der Höhendifferenz h ist. v0=w*ra-w*rb = w*(rb+h)-w*rb = w*h. Der Versatz am Boden ist dann s=v0*Wurzel(2*h/g) = w*h*Wurzel(2*h/g). Für die Erde ist w=2pi/T=7,29*10^-5/s. Bei h=10m ist s=1mm, bei 50m sind es 12mm und bei h=100m sind es 33mm. Aber nur am Äquator. Fällte der Apfel in die hohle Erdachse gibt's keine Bahngeschwindigkeit und der Effekt fällt aus, dazwischen ist v0=w*h*cos(Breite). Soweit richtig?
Das schöne an Hookes Ansatz ist, dass man fast im Kopf rechnen kann. Fällte der Apfel jetzt in die leere Erdachse, dann wird er entlang der 6400 km erst mit 10 m/s^2 beschleunigt, im Zentrum mit null, dann geht's wieder aufwärts zur anderen Seite. Die mittlere Beschleunigung ist a=5m/s^2 und er erreicht im Zentrum eine Geschwindigkeit von v=Wurzel(2*a*R)=8km/s, was auch die 1. KG ist. Die komplette Schwingung dauert 2pi*Wurzel(R/g) oder etwa 5000 Sekunden, nach 84 Minuten ist der Apfel also wieder zurück. Und genau so lange braucht auch der Satellit nahe der Oberfläche für eine Umrundung der Erde.
Selbst die Differenz des Gravitationspotentials kann man mit Hookes Methode bestimmen. Die Energie der virtuellen Feder ist unten null und oben D*R^2/2=m*g*R/2, die Potentialdifferenz ist dann U=E/m=g*R/2. An der Oberfläche ist das Potential g*R, im Zentrum also 1,5 mal so groß wie oben, der gleiche Wert ergibt sich auch aus (g+a)/g.
Und um wieviel geht eine Uhr im Zentrum nach pro Tag? Wie groß ist der Zeitversatz der 'Uhr im Apfel', wenn sie nach 84 Minuten wieder ankommt? Doch nicht etwa die gleiche wie bei der im Satellit nach seiner Runde? Und wieso geht die Uhr an Bord eines Satelliten mit einem Orbit von (schon wieder diese Zahl) 1,5-fachem Erdradius genauso schnell wie die Vergleichsuhr der Bodenstation?
Die (Feder-)Spannung wächst. Aber Hooke und Newton verstehen die Frage gar nicht...
Hab' ich jetzt 'ursprünglich verstanden' und 'exakt gedacht' oder die teuflischen Details übersehen?
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 24. März 2006 03:47 Titel: Opa Verfasst am: 24. März 2006 03:47 Titel: |
 |
|
O, Ihr Könige der Physik, habt Ihr das schnell gerechnet, vielen, vielen Dank!
Ich mußte, um es nachzuprüfen zu können, mir tatsächlich den Kosinussatz wieder beibringen. Puh, was für eine Arbeit für die alten grauen Zellen. Euren eleganten Weg konnte ich nicht nehmen, der war mir zu hoch. So bin ich denn den niederen Weg gegangen und fing an, umständlich in Excel, mit Eurer Lösung 61, den Erdradius zu 6378 km genommen.
=cos(BOGENMASS(61)) mal 6378 mal 2 mal Pi = Umfang des Breitenkreises; diesen geteilt
durch 24 Std, durch 60 Minuten, durch 60 Sekunden; mal 1000 = 224,856 Meter pro Sekunde.
Bitte, kann mir jemand sagen ob das stimmt?
Ich hatte zuerst immer das Doppelte raus, 449 Meter pro Sekunde und dachte schon, Tycho Brahe hätte eine Reise zum Äquator unternommen, um sich einmal ordentlich, mit mehr als Schallgeschwindigkeit, herumschleudern zu lassen; - ich hatte den passus, den Doppelschritt der römischen Soldaten, doppelt genommen. Tycho war übrigens noch in Dänemark geboren, da Schonen erst 1658 an Schweden fiel.
Anschließend gelang es mir, eine excellige Vereinfachung zu komponieren:
In der einen Spalte (B..) stehen nun Zahlen für die Breitenkreise, 0, 10, 20... 61, bis 89,9; und in der zweiten Spalte steht pro Zelle daneben
=(COS(BOGENMASS(B..))*147,63889*PI()).
Ein kleines Herumschleudermaschinchen, ich hoffe, es stimmt, es zeigt jedenfalls die gleichen
Meterzahlen an wie oben. Ob jemand das auch nachprüfen will? Denn ich weiß schon nicht mehr, wie es gelingen konnte, alles in einer Zelle unterzubringen. Teufel auch, mein Gedächtnis läßt nach.
Luther: „ ... das ganze Firmament so schnell und behend bewegt, und in 24 Stunden umher läuft, in einem Huy und Nu, etliche tausend Meile-Wegs, welches vielleicht von einem Engel geschieht.“
Kepler schlug sich so damit herum: „...wird es geschehen, daß der Stein beim Herabfallen ein wenig von dem Lot abweicht, das man vom Mittelpunkt der Erde durch ihre Oberfläche nach dem Mittelpunkt des Steins zieht, und daß das Lot des Steins allmählich auf weiter westlich liegende Teile der Erdoberfläche trifft, wenn sich die Erde vom Westen nach Osten bewegt; es wird der Erde nicht vollkommen folgen, sondern von ihr zurückgelassen werden.“
(11. Oktober 1605).
Ihr habt’s ja schon bemerkt, hier irrte selbst der kaiserliche Mathematiker. Allerdings bemerkte er den Irrtum und versuchte ihn aufzulösen, was ihm nur auf eine künstliche, verworrene Weise gelungen sein soll, da er vom Beharrungsgesetz noch nichts wußte.
Der große Newton erst ... Davon später. Herzlichen Gruß in die Runde!
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 24. März 2006 09:18 Titel: dermarkus Verfasst am: 24. März 2006 09:18 Titel: |
 |
|
| Opa hat Folgendes geschrieben: |
=cos(BOGENMASS(61)) mal 6378 mal 2 mal Pi = Umfang des Breitenkreises; diesen geteilt
durch 24 Std, durch 60 Minuten, durch 60 Sekunden; mal 1000 = 224,856 Meter pro Sekunde.
Bitte, kann mir jemand sagen ob das stimmt?
|
Das kann ich voll bestätigen.
| Opa hat Folgendes geschrieben: |
Anschließend gelang es mir, eine excellige Vereinfachung zu komponieren:
In der einen Spalte (B..) stehen nun Zahlen für die Breitenkreise, 0, 10, 20... 61, bis 89,9; und in der zweiten Spalte steht pro Zelle daneben
=(COS(BOGENMASS(B..))*147,63889*PI()).
|
Auch hiermit bin ich voll und ganz einverstanden.
| Opa hat Folgendes geschrieben: |
Kepler schlug sich so damit herum: „...wird es geschehen, daß der Stein beim Herabfallen ein wenig von dem Lot abweicht, das man vom Mittelpunkt der Erde durch ihre Oberfläche nach dem Mittelpunkt des Steins zieht, und daß das Lot des Steins allmählich auf weiter westlich liegende Teile der Erdoberfläche trifft, wenn sich die Erde vom Westen nach Osten bewegt; es wird der Erde nicht vollkommen folgen, sondern von ihr zurückgelassen werden.“
(11. Oktober 1605).
|
Und sogar hier verstehe ich Kepler so, dass er recht hat: Er sagt, das Lot unter dem fallenden Stein trifft weiter im Westen auf als der fallende Steins. Also trifft die Flugbahn des fallenden Steins weiter im Osten auf als das Lot. Und das sagt auch die Rechnung im rotierenden Bezugssystem mit der Corioliskraft und Gasts Überlegung im nicht rotierenden Bezugssystem mit den radial unterschiedlichen Bahngeschwindigkeiten: Der Auftreffpunkt des fallenden Steines liegt ein kleines Stückchen weiter östlich als der Auftreffpunkt des genau senkrechten Lots unter seinem Startpunkt.
Da darf ich also gleich dreimal zur Richtigkeit gratulieren 
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 24. März 2006 10:18 Titel: dermarkus Verfasst am: 24. März 2006 10:18 Titel: |
 |
|
| Anonymous hat Folgendes geschrieben: |
Der Coriolis-Effekt ist ein Trägheitseffekt, der auf der radiusabhängigen Bahngeschwindigkeit beruht. Solche Trägheitskräfte sind Scheinkräfte in rotierenden Systemen und führen bei radialer Bewegung in Richtung Zentrum zur Ablenkung in Richtung der Rotation.
|
Damit bin ich voll und ganz einverstanden. Im nicht mitrotierenden Bezugssystem ergibt sich damit folgende Herleitung für die Richtung der Corioliskraft: Die Bahngeschwindigkeit, die einer Rotation mit einer bestimmten Winkelgeschwindigkeit entspricht, nimmt nach außen hin zu.
Die Bahngeschwindigkeit des Apfels entspricht der Winkelgeschwindigkeit der Erde mal seinem anfänglichen Abstand vom Mittelpunkt der Erde. Fällt er hinunter, so ist er mit seiner horizontalen Geschwindigkeit schneller als die unten erforderliche Bahngeschwindigkeit, und er eilt der Drehung der Erde voraus. Wirft man ihn nach oben, so ist er mit seiner horizontalen Geschwindigkeit langsamer als die dort oben erforderliche Bahngeschwindigkeit, und er bleibt hinter der Drehung der Erde zurück.
Wir sehen: Bewegt man sich von der Erdachse weg, so wirkt die Corioliskraft nach Westen, bewegt man sich zur Erdachse hin, so wirkt die Corioliskraft nach Osten.
| Anonymous hat Folgendes geschrieben: | Günstigerweise haben wir diesen Fall hier nicht, unser Bezugssystem, der Erdboden, rotiert mit, und dort messen wir ja den Versatz. (...)
Nichts anderes beschreibt auch der waagerechte Wurf nach Osten, wobei die Startgeschwindigkeit (... ). Soweit richtig?
|
Leider was das Bezugssystem angeht nicht ganz richtig. Gast rechnet hier in einem nicht rotierenden Bezugssystem, das sich mit der Geschwindigkeit geradeausbewegt, die in Richtung und Betrag der Geschwindigkeit der Erdoberfläche zum Startzeitpunkt des Apfels entspricht. Die Rotationsbewegung der Erde berücksichtigt er aber nur ganz am Anfang für die Startgeschwindigkeit des Apfels. Die anschließende Rotation, insbesondere also auch die Veränderung der Richtung der Erdbeschleunigung im verwendeten Bezugssystem, vergisst er daher zu berücksichtigen.
Für die eine Sekunde Fallzeit aus unserer Aufgabenstellung ist die Fallhöhe 25 m. Der Apfel hat also, wie Gast richtig als Formel herleitet, oben am Startpunkt eine um v_0 = omega * h = 1,8 mm/s größere Bahngeschwindigkeit als die Erdoberfläche unter ihm. Und er trifft also nach Gasts Rechnung 1,8 mm östlich vom Fußpunkt des Lotes unter seinem Startpunkt auf. Dieser Wert ist nicht nur ein bisschen, sondern deutlich zu groß, wie ein Vergleich mit der Rechnung im rotierenden Bezugssystem zeigt:
-------------------------------------------------------------------------
Rechnung im rotierenden Bezugssystem mit der Corioliskraft:
Im mit der Winkelgeschwindigkeit omega der Erde mitrotierenden Bezugssystem ist sowohl die Anfangsgeschwindigkeit der Erdoberfläche als auch die Anfangsgeschwindigkeit des Apfels genau Null. Die Gravitationsbeschleunigung wirkt immer genau in dieselbe Richtung und bewirkt die Bewegung in senkrechter Richtung mit der Geschwindigkeit
 = g\cdot t )
Die Corioliskraft ist
 = m \cdot \vec a_c )
Damit zeigt die Coriolisbeschleunigung in horizontale Richtung (für die hier vorliegende Fallbewegung nach Osten, das überlegt man sich mit den Regeln für die Vektoren des Kreuzproduktes; die Drehachse der Erde zeigt von Süden nach Norden), und ihr Betrag ist:
 \cdot \omega \cdot g \cdot t )
Dabei ist phi wieder wie oben der Winkel, der den Breitengrad auf der Erde angibt, denn mit dem Winkel alpha zwischen Bewegungsrichtung und Richtung der Drehachse gilt : sin(alpha) = cos(phi).
Zweimal nach der Zeit integrieren liefert die bei dieser beschleunigten horzontalen Bewegung zurückgelegte Strecke:
 \cdot \omega \cdot g \cdot \frac{1}{6}t^3 )
Mit der Winkelgeschwindigkeit der Erde omega = 7,27 * 10^-5 (1/s), der Erdbeschleunigung g=9,81 m/s^2, der Flugzeit t=1 s und am Äquator (Breite phi = 0° und damit cos(phi)= 1) erhält man damit durch einsetzen:

Die Rechnung im rotierenden Bezugssystem ergibt also einen Auftreffpunkt des Apfels 240 Mikrometer östlich vom Fußpunkt des Lotes unter dem Startpunkt.
|
|
 |
Gast
|
 Gast Verfasst am: 24. März 2006 15:43 Titel: Gast Verfasst am: 24. März 2006 15:43 Titel: |
 |
|
Sehr gut, danke Markus, man lernt nie aus..
Ich war Galileis Gedanken gefolgt, und das trifft hier klar daneben. Im Bild unten sieht man warum das so ist.
Die 'flache Erde' Vereinfachung liefert s=w*h*Wurzel(2*h/g), aber die 'rückwärts' gerichtete Beschleunigung nimmt 1/3 davon wieder weg, und dadurch bleibt nur noch s=(2/3)*w*h*Wurzel(2*h/g) übrig. Das w für die Erde ist 2pi/86164s = 7,292*10^-5/s, h=10m bringt s=0,7mm, bei 25m sind es 2,7mm, bei 50m 7,8mm und bei h=100m ist s=22 mm, alles am Äquator und mit g=9,81m/^2, sonst mal cos(Breite).
Hier ist ein Stück Text, der auch den Beitrag von Robert Hooke unterstreicht:
"The 'backward' acceleration reduces the 3 cm deflection by 1 cm to 2 cm [h=100m], just as given by the Coriolis effect. But more interesting, retarding in its eastward motion, the object will, seen from outside the Earth, follow an elliptic path. The first to realize this was two famous British scientists, Robert Hooke and Isaac Newton. In November 1679 Robert Hooke, in his capacity as newly elected Secretary of the Royal Society, tried to draw Isaac Newton into a discussion on the motions of the planets and comets. But Newton had just returned from a long vacation at his family home in Lincolnshire - where he incidentally might have watched apples fall in the garden. Perhaps inspired by these falling apples he had something else on his mind, 'a fancy of my own', the horizontal deflection of objects dropped from a high altitude as proof of the Earth's rotation. The exchange of letters that followed during the winter 1679-80 between Newton and Hooke shows that it was thanks to Hooke, they came to realise that the fall of the body must be treated as an elliptic orbit with the centre of the Earth in one of its focii.
From the insight that a falling object in absolute space follows the same type of orbit as any of the planets or comets around the Sun, it was possible for Newton to infer that the motions of all terrestrial and extra-terrestrial bodies might be controlled by the same mechanism, universal gravitation. He never discovered the Coriolis effect, but looking for it found the laws of motion." [1]
Und dies hier ist aus 'Technische Physik', da steckt anscheinend noch Galileis Vereinfachung drin:
"Entdeckt wurde die Corioliskraft bei der Untersuchung unerklärlicher Abweichungen von Geschossbahnen, da beim Abschießen nach Norden stets eine Ostabweichung und beim Abschießen nach Süden stets eine Westabweichung auftritt."
"Lässt man einen Stein von einem Turm fallen, so fällt er nicht genau senkrecht, sondern wird etwas nach Osten abgelenkt. Bei 100m Höhe und einer nördlichen Breite von 54° ergibt sich eine Abweichung von 1,9 cm."
Richtig wäre eher 1,3 cm. Oder ist das auch noch viel zu viel? Der Irrtum ist immer und überall.
> "Für die eine Sekunde Fallzeit aus unserer Aufgabenstellung ist die Fallhöhe 25 m." Wirklich?
Eine Sekunde entspricht doch 5m Fall, und dafür stimmen die 0,24mm, bei 25m sind es dann 2,7mm.
[1] Anders Persson, The Coriolis Effect – a conflict between common sense and mathematics.
Daraus ist auch das folgende Bild komponiert. Dort steht auch zu lesen: "It is not commonly known that Leonard Euler already in 1749 derived analytically what was essentially the Coriolis acceleration", belegt mit einem Text von Euler.
| Beschreibung: |
|

Download |
| Dateiname: |
freefall.jpg |
| Dateigröße: |
16.27 KB |
| Heruntergeladen: |
5837 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 24. März 2006 16:23 Titel: dermarkus Verfasst am: 24. März 2006 16:23 Titel: |
 |
|
Das macht ja richtig Spaß mit so vielen schönen und fundierten Zitaten hier!
| Anonymous hat Folgendes geschrieben: |
Richtig wäre eher 1,3 cm. (...)
Eine Sekunde entspricht doch 5m Fall, und dafür stimmen die 0,24mm, bei 25m sind es dann 2,7mm.
|
Vielen Dank, Gast, eine Sekunde entspricht natürlich in der Tat 5 m Fall! (Ich habe den Eindruck "Gemeinsam sind wir stark"  ) Ich bin auch einverstanden mit den Werten 1,3 cm für 100 m Fall und 2,7 mm für 25 m Fall. ) Ich bin auch einverstanden mit den Werten 1,3 cm für 100 m Fall und 2,7 mm für 25 m Fall.
Mein Absatz von oben muss dann dementsprechend korrigiert lauten:
Für die eine Sekunde Fallzeit aus unserer Aufgabenstellung ist die Fallhöhe s= (g/2)*(1 s)^2 = 5 m. Der Apfel hat also, wie Gast richtig als Formel herleitet, oben am Startpunkt eine um v_0 = omega * h = 0,36 mm/s größere Bahngeschwindigkeit als die Erdoberfläche unter ihm. Und er trifft also nach Gasts Rechnung 0,36 mm östlich vom Fußpunkt des Lotes unter seinem Startpunkt auf. Dieser Wert ist um den Faktor 3/2 zu groß.
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 24. März 2006 17:12 Titel: Opa Verfasst am: 24. März 2006 17:12 Titel: |
 |
|
> Er sagt, das Lot unter dem fallenden Stein trifft weiter im Westen auf als
der fallende Steins. <
Da hat dermarkus aber eine feinsinnige Spitzfindigkeit für mich eingebaut.
Zuerst möchte ich ihm und dank seiner Hilfe auch Opa zweimal Glückwünsche aussprechen!! Kepler unterscheidet in seinem Satz zwei Lote, meine ich. Einmal spricht er von d e m Lot, und er beschreibt dieses ganz genau. Dann bezieht er sich nur noch auf das Lot des Steins, das allmählich ... Mit allmählich drückt er wohl aus, wie der Stein sich nach und nach wieder der Erde nähert. Das Lot, das am Stein hängend gedachte, trifft kurz vor und auch während des Auftreffens des Steins auf weiter westlich liegende Teile der Erdoberfläche. Entscheidend ist damit: Der Stein trifft westlich auf. Kepler selbst hat später diesen Widerspruch bemerkt und zu korrigieren versucht.
Ist diese Sache nun ganz klar, dann dritter Glückwunsch!
Tycho und Kepler konnten die Sache nicht richtig lösen, es fehlte ihnen das Beharrungsgesetz, die Vorstellung oder die Tatsache der Trägheit.
Es war der große Newton, der 1679 der Royal Society ein wirklich entscheidendes Experiment vorschlug, doch die Physiker waren 112 Jahre lang gehindert oder zu faul, es durchzuführen. 1903 im Pantheon in Paris fand der letzte Versuch in dieser Frage statt.
Opa findet es bedenkenswert, von Tycho und Kepler 1600 bis Flammarion 1903 sind immerhin 300 Jahre vergangen, bis es den tüchtigen Physikern gelang, die Sache durch Experimente zu beweisen.
Gast mit der Frage nach ursprünglichem Denken, möge bedenken, um welche wichtige Sache es ging, und wie man sie dann mit exaktem Denken Kindern nahebringen kann, nicht den speziellen Physikkindern, sondern „allen“ Gymnasialkindern oder Hauptschülern.
Damit auch die Rechner mit Formeln nicht zu kurz kommen, darf ich um Nachprüfung des Ergebnisses von Guglielmini 1791 / 92 in Bologna bitten? Phi = 40 Grad und 30 Sekunden.
Fallhöhe 78,3 Meter. Beobachtete Abweichung 19 + - 2,5 mm, nach 16 Versuchen.
Berechnet?
Oh, neue Zeichnungen, wie herum dreht sich die Erde?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 24. März 2006 17:33 Titel: dermarkus Verfasst am: 24. März 2006 17:33 Titel: |
 |
|
Die Sonne geht im Osten auf, also dreht sich die Erde nach Osten.
Newtons "Lot des Steins" lässt sich schön auf der rechten Seite in Gasts Bild wiederfinden: Die senkrecht zur Erdoberfläche gemeinten Striche und Pfeile zeigen die Richtung des Lots des Steins an, während der Stein fliegt.
Der Stein fliegt nach Osten. Also zeigt zu jedem Zeitpunkt des Fluges das Lot des Steins auf Punkte, die westlich vom Auftreffpunkt des Steines liegen.
Guglielminis Messung lässt mich grummeln und vermuten, dass er Galileis Theorie gekannt hat und seine Messfehler zu klein eingeschätzt hat. Denn meine Rechnung ergibt 12 mm.
|
|
 |
Gast
|
 Gast Verfasst am: 24. März 2006 18:56 Titel: Gast Verfasst am: 24. März 2006 18:56 Titel: |
 |
|
Hartmut v. Hentigs Motto: "Die Sachen klären, die Menschen stärken."
> wie herum dreht sich die Erde?
Zwei Menschen stehen sich gegenüber, einer guckt nach Norden, der andere nach Süden.
Für beide dreht sich die Erde nach Osten, für einen nach rechts, für den anderen nach links.
Im Süden steht die Mittagssonne im Norden. Aber da ist ja auch Weihnachten im Sommer..
Die Landkarte ist nicht die Landschaft, die Theorie nicht die Realität.
Im Spiegel ist doch links und rechts vertauscht, warum nicht auch oben und unten?
(-; Vorsicht, doppelter Boden ;-)
> .. Abweichung 19 + - 2,5 mm, nach 16 Versuchen.
Luft im Spiel. Macht das was?
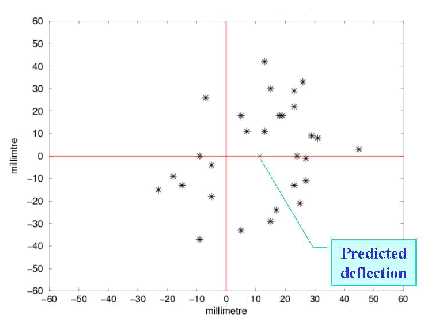
Hier ist noch so ein Experiment, 1803 in Schlebusch (51°), Schacht 90 m tief, 29 Eisen-Murmeln (?).
| Beschreibung: |
|
| Dateigröße: |
9.36 KB |
| Angeschaut: |
13006 mal |
|
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 24. März 2006 22:54 Titel: Opa Verfasst am: 24. März 2006 22:54 Titel: |
 |
|
O, bei der Zeichnung hab ich wohl zu schnell geguckt und voreilige Schlüsse gezogen.
Bitte um Entschuldigung!
Für Bologna gibt Wagenschein einen berechneten Wert von 11,3 an,
für Schlebusch, Phi = 51° 25’ , Benzenberg 1804, Fallhöhe 85,1 m; östliche Abweichung beobachtet: 11,5 +-2,9; berechnet 10,4 mm; 29 Versuche.
Leider kann ich die Rechnung nicht nachmachen. Kann mir jemand dabei helfen? In möglichst einfachen für mich verständlichen Schritten. Wenn’s aber zu kompliziert ist, dann lieber nicht. Es reicht im Grunde ja die Überzeugung aus, daß es eine nachgewiesene Ostabweichung gibt, um damit einen Beweis für die Drehung der Erde zu haben, der von Kindern eingesehen werden kann, nach vielerlei anderen verstandenen Vorbereitungen auf dem Wege dahin natürlich erst. Wie kann man deutlich machen, daß der Apfel am Baum eine höhere Geschwindigkeit hat als der Erdboden. Warum behält er diese höhere Geschwindigkeit bei, noch lange bei, nachdem er abgefallen ist. Wie kommt es, daß die Erde sich immer dreht, ihre Bewegung überhaupt nicht vergessen kann. Komplizierte Zusammenhänge, aber alle ohne Formeln zu verstehende.
Noch mehr Berichte, die ich gerne nachrechnen möchte, wenn ich’s denn noch lernen kann.
Hall 1902, Cambridge (Mass.) Phi = 42° 22’ .8 ; Zahl der Versuche 948; Fallhöhe 23 m;
beobachtet: 1,5 +- 0,05 mm; berechnet 1,77 mm.
Reich, 1831, Freiburg i. S. Phi = 50° 33’ .1; Versuche 106; Fallhöhe 158,5 m; Östl. Abw. beob. 28,3 +-4; berechnet 27,4 mm.
Flammarion 1903, Paris, Phi = 48° 50’ .8 ; Versuche 144; Fallhöhe 68 m;
Östl. Abw. beob. 6,3; berechnet 8,1 mm.
Benzenberg 1802 in Hamburg kennt man sicherlich.
Zur letzten Angabe findet man in Wagenscheins Buch eine Zeichnung im Maßstab 1:1, ganz ähnlich der von Schlebusch, nur halt mit 144 Einschlägen.
Das Buch ist vergriffen, auch in den Netz-Antiquariaten, soweit ich sehen konnte. Irgendwo wurden Vorbestellungen für eine Neuauflage gesammelt.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 24. März 2006 23:41 Titel: dermarkus Verfasst am: 24. März 2006 23:41 Titel: |
 |
|
| Anonymous hat Folgendes geschrieben: |
Luft im Spiel. Macht das was?
|
Ja, der Luftwiderstand vergrößert den Wert tatsächlich ein bisschen. Aber für Bleikugeln mit Radius 1 cm nicht so sehr, dass das den gerundeten Wert 12 mm verändern würde. (Für diese Abschätzung habe ich zugegebenermaßen meinen Computer numerisch rechnen lassen)
Aber das beruhigt mich ja, dass das Ergebnis des Bologna-Experimentes laut Opa nun mit den rund 12 mm übereinstimmt.
-----------------------------------------------------------
Nachrechnen kann man das so:
Die Fallzeit berechnet man aus der Fallhöhe h mittels:

Die Winkelgeschwindigkeit der Erde  = 7,27 * 10^-5 (1/s), die Erdbeschleunigung g=9,81 m/s^2, und die geographische Breite = 7,27 * 10^-5 (1/s), die Erdbeschleunigung g=9,81 m/s^2, und die geographische Breite  kennt man ebenfalls. kennt man ebenfalls.
Das (also t,  , g und , g und  ) setzt man alles in folgende Formel ein ) setzt man alles in folgende Formel ein
 \cdot \omega \cdot g \cdot \frac{1}{3}\cdot t^3 )
und das s_c , das man durch Eintippen in den guten alten Taschenrechner (so mache ich das normalerweise) oder wie moderne Menschen mit einem Programm wie Excel berechnet, ist das gewünschte Ergebnis.
---------------------------------------------------
Nun noch ein bisschen was anschauliches:
| Opa hat Folgendes geschrieben: | Wie kann man deutlich machen, daß der Apfel am Baum eine höhere Geschwindigkeit hat als der Erdboden.
|
Das ist so wie bei einem großen Karussell: Wenn man weiter außen sitzt, dann pfeift einem der Fahrtwind schneller um die Ohren.
| Opa hat Folgendes geschrieben: |
Warum behält er diese höhere Geschwindigkeit bei, noch lange bei, nachdem er abgefallen ist.
|
Weil ihn keiner stark genug bremst (die Luft bremst nur ein kleines bisschen, nur die Erdanziehung muss man richtig mitberechnen, wenn man in schiefen Bezugssystemen rechnet). Und solange ein Körper nicht gebremst oder abgelenkt wird, fliegt er mit seiner Geschwindigkeit immer weiter geradeaus, das ist Newtons Gesetz der Trägheit.
| Opa hat Folgendes geschrieben: |
Wie kommt es, daß die Erde sich immer dreht, ihre Bewegung überhaupt nicht vergessen kann. |
Das liegt ebenfalls daran, dass sie keiner bremst (Der Mond und die Sonne bremsen ihre Drehung ein gaaanz ganz kleines bisschen durch die Reibung der Gezeitenkräfte, aber das ist nur mit hochpräzisen Messungen feststellbar.) Also ebenfalls eine Art Trägheitsgesetz. Für Drehungen nennt man das Drehimpulserhaltung.
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 25. März 2006 22:24 Titel: Opa Verfasst am: 25. März 2006 22:24 Titel: |
 |
|
Ich lerne viel dazu bei Euch, Ihr edlen Herren, und dafür danke ich sehr!
Nun konnte ich mit der Formel tatsächlich doch noch etwas anfangen; für omega nahm ich
allerdings 2 Pi/ 86400, dann gibt’s noch mehr Stellen hinter dem Komma und man hat noch einen Bezug zum Umfang und zu den 86400 Sekunden einer täglichen Erdumdrehung.
Ich habe alle bei Wagenschein gegebenen berechneten Werte nachprüfen können. Meine ‚modernen’ Excelrechnungen ergaben geringfügige Abweichungen von seinen Werten, in Cambridge (Mass.) 0,013 mm; in Paris, Pantheon 0,020 mm.
Dann eine etwas größere Abweichung von den vorgegebenen Werten, Bologna 0,233 mm.
Noch etwas mehr abweichend: Schlebusch 0,317 mm und Freiburg i. S. 0,350 mm.
Wer sagt mir, ob diese Abweichungen toleriert werden können?
> Das ist so wie bei einem großen Karussell: Wenn man weiter außen sitzt, dann pfeift einem der Fahrtwind schneller um die Ohren. <
Ein schöner Einfall. Indes läßt sich diese „handgreifliche“ Erfahrung kaum in einer Schulstube bewerkstelligen. Darf ich daher vielleicht einen Fahrradreifen als Zwischenmodell vorschlagen?
> Im Spiegel ist doch links und rechts vertauscht, warum nicht auch oben und unten? <
Ach, lieber Gast, im Buche von Martin Gardner „Das gespiegelte Universum“ (deutsch 1967) gibt es Spiegel, die auch oben mit unten vertauschen.
Ich grüße Euch und danke noch einmal. Sicher kann ich noch viel mehr hier lernen.
> Taschenrechner < Welche Tasten muß ich drücken bei der Formel von der markus?
Wenn’s denn keinen Aufwand macht, könnte man gar die 5 Werte, von Cambridge bis Freiburg nachrechnen? In Bologna, fällt mir ein, da war ich schon mal.
Inzwischen plage ich mich mit einer wirren Frage herum. Könnte sein, daß jemand darüber mehr Bescheid weiß: Seit wann gibt es eigentlich unser Zehnerstellenwertsystem?
|
|
 |
Gast
|
 Gast Verfasst am: 26. März 2006 01:08 Titel: Gast Verfasst am: 26. März 2006 01:08 Titel: |
 |
|
> Seit wann gibt es eigentlich unser Zehnerstellenwertsystem?
Das Internet ist eine gigantische Bibliothek, voller Fug wie gleichermaßen Unfug, und man findet was immer man sucht. Und man lernt dabei, nicht etwas schon deshalb zu glauben, weil es 'da steht', und folgend auch, hoffentlich, nicht alles zu glauben was man denkt.
Mit dieser Warnung vorab, es sieht so aus, als stamme das Stellenwertsystem von den Sumerern aus der Zeit 3100-2800 BCE, aber benutzt auf Basis 60. Das daraus abgeleitete Zwölfer-System (fünf dutzend) ist heute noch erkennbar an den einsilbigen Zahlen bis zwölf, dann zweisilbig weiter mit dreizehn. Andere Beispiele sind die Uhrzeit und die Winkelteilung. Das Dezimalsystem mit zehn Symbolen, aber noch ohne die Null als Platzhalter, scheint aus China zu kommen und hat uns über Indien vermittelt durch die Araber erreicht. Was wir 'arabische Zahlen' nennen, wird auf Arabisch 'indische Zahlen' genannt.
 http://www.computersmiths.com/chineseinvention/images/zero.jpg http://www.computersmiths.com/chineseinvention/images/zero.jpg
Im Bild ein Art Kalender aus dem 13. Jahrhundert BCE, das Symbol 0 ist darin schon zu finden, aber es scheint für die Zehn zu stehen, denn als Platzhalter diente das wichtigste aller Zeichen in jeder Schriftsprache, das Leerzeichen. Ein Zeitraum von 547 Tagen ist hier notiert als 'fünf hundert und vier Dekaden und sieben der Tage'. Die Verwendung der Null als Platzhalter scheint indischen Ursprungs zu sein.
Was das Nachrechnen betrifft, das verlangt nach einem Rechner, der mit Exponenten klarkommt, sonst wird es mühsam. Ich habe zum Ausrechnen die Gleichung s=(2/3)*w*h*Wurzel(2*h/g) verwendet, worin h die Höhe in Meter ist, g die Erdbeschleunigung mit 9,81 m/s^2 und w die Winkelgeschwindigkeit der Erde 2pi/86164s = 7,292*10^-5/s. Die 86164 Sekunden entsprechen dem Sternentag, der Sonnentag mit 86400 Sekunden ist hier eigentlich nicht angebracht, aber das nur im Sinne von 'exaktes Denken', weniger wegen der Genauigkeit des Ergebnisses, denn die anderen Fehler sind bestimmt größer, so ist z.B. ist die Erdbeschleunigung ortsabhängig. Der einzige Vorteil der genannten Gleichung ist, dass man meist die Höhe schon hat und die Zeit hoch drei nicht braucht, dafür aber die Wurzel, doch die ist meist vorhanden. Wenn der Rechner keine Exponentendarstellung kennt müsste man w als 0,00007292 eintippen. Eine andere Möglichkeit wäre 0,07292 zu tippen, dann bekommt man das Ergebnis in Millimeter, was ja auch nicht schlecht ist. Was die Reihenfolge der zu drückenden Tasten angeht muss ich leider passen denn ich verwende schon immer einen RPN Rechner, da ist alles anders (und viel einfacher), aber das verwirrt anfangs.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 26. März 2006 01:23 Titel: dermarkus Verfasst am: 26. März 2006 01:23 Titel: |
 |
|
Ein Fahrradreifen ist natürlich auch ein schönes Modell. Nur wollte ich mich da dann ungern selbst draufsetzen, um den Fahrtwind zu erspüren 
Das Dezimalsystem kommt aus Indien. Laut Wikipedia wurde es dort um 600 n.Chr. erfunden und kam über Arabien nach Europa. Erste Ansätze eines Zehnersystems gab es bereits im alten Ägypten, im alten Rom und in China.
http://de.wikipedia.org/wiki/Dezimalsystem#Geschichte
Die kleinen Abweichungen von Opas Rechnungen können mit sehr ruhigem Gewissen toleriert werden. (Ich komme selbst beim Nachrechnen auf Abweichungen derselben Größenordnung.) Denn zum einen ist ja die Messgenauigkeit der Ergebnisse, die damit verglichen werden, nicht genauer als diese Abweichungen, und zum anderen haben wir die Werte, die wir zum Einsetzen in diese Formeln verwendet haben, auch nur auf zwei geltende Ziffern genau gekannt.
Denn 1) die Fallhöhe war in manchen Fällen nur in ganzen Metern gegeben, 2) die Winkelgeschwindigkeit der Erde ist ganz genaugenommen
omega_siderisch = 2*Pi / (86164,099 s) = 7,2921 * 10^-5 (1/s)
(denn der Sonnentag entspricht nicht ganz genau der Zeit, indem sich die Erde einmal um sich selbst dreht, weil die Erde sich gleichzeitig um die Sonne bewegt)
und 3) die Erdbeschleunigung g variiert leicht von Stadt zu Stadt, nicht nur mit der Höhe, wie wir schon wissen, sondern auch mit der geographischen Breite (weil die Erde am Äquator einen größeren Durchmesser hat als von Pol zu Pol) und mit der genauen Beschaffenheit des Gesteins in der Erdkruste unter dieser Stadt. Auch diese Variation zeigt sich in leichten Schwankungen der dritten geltenden Ziffer von g=9,81 m/s^2 von Ort zu Ort.
Innerhalb der Genauigkeit, mit der wir unsere eingesetzten Werte gekannt haben, sind diese kleinen Rechenabweichungen also absolut tolerabel.
Das Beispiel Bologna tippe ich folgendermaßen ein:
2
X
7
8
.
3
/
9
.
8
1
=
Wurzeltaste
(Nun stehen da die rund 3,995 Sekunden für t.)
Taste "y hoch x"
3
X
4
0
.
5
cos
X
2
X
Taste "PI" (oder 3.14159 eintippen)
/
8
6
4
0
0
X
9
.
8
1
/
3
=
Und dann stehen da die 0,011533 m, die ich gerundet als 12 mm angebe.
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 26. März 2006 12:15 Titel: Opa Verfasst am: 26. März 2006 12:15 Titel: |
 |
|
Mit viel Liebe zur Sache fühle ich mich hier sehr gut behandelt, danke!
Am Taschenrechner mußte ich nach y^3 noch = drücken, dann kam am Ende ebenfalls 11, 533 mm exakt heraus.
Fahrradreifen, das war ganz schlecht von mir formuliert, pardon, da muß man sich selbstverständlich dessen Innereien mitdenken; außen der sich schnell drehende Reifen, samt den oberen Speichenenden, in der Mitte die anscheinend langsamer drehende Nabe. Wenn man in alten Filmen Postkutschenräder sieht, dann scheinen die manchmal gar rückwärts zu drehen.
Mit dem Sternentag zu 86164 Sekunden werde ich gleich nachrechnen. Hab ich schon. Es stellte sich eine merkwürdige Erscheinung ein. Die Abweichungen (von Wagenscheins Werten) bei Paris und Cambridge wurden noch geringer; die anderen drei Abweichungen aber wurden im Gegensatz dazu größer, komisch. Und an der Spitze mit den geringsten Abweichungen, sortiert nach der Entfernung des Minuszeichens, da liegt jetzt Paris vor Cambridge, anders als vorher.
Erdtag......ber. ......Abw........Orte................sortiert
mm..........Wag.....v.Wag......d. Versuche......nach Abw.
______________________________________________________
1,7840....1,77.....0,0140.....Cambridge.......0,0140.....Cambridge
8,0796....8,1......-0,0204.....Paris...............0,0204.....Paris
10,805....10,4.......0,4055.....Schlebusch.......0,2330.....Bologna40,5
11,533....11,3.......0,2330.....Bologna40,5.....0,3501.....Freiburg i. S.
27,7501...27,4......0,3501.....Freiburg i. S......0,4055.....Schlebusch
Sterntag...ber. ......Abw........Orte................sortiert
mm..........Wag.....v.Wag......d. Versuche......nach Abw.
______________________________________________________
1,7889......1,77...0,0189......Cambridge.......0,0018.....Paris
8,1018......8,1....-0,0018......Paris...............0,0189.....Cambridge
10,8351....10,4......0,4351.....Schlebusch.......0,2646.....Bologna40,5
11,5646....11,3......0,2646.....Bologna40,5.....0,4261.....Freiburg i. S.
27,8261....27,4......0,4261.....Freiburg i. S.....0,4351.....Schlebusch
Ich kann mir diese Merkwürdigkeit nicht erklären, Teufel auch, hab ich den Fehler gemacht,
kann Excel nicht mehr richtig rechnen und sortieren, oder liegt es an den Formeln oder an Wagenscheins berechneten Werten oder sonstwo dran? Natürlich möchte auch ich exakt denken können in dem Sinne, wie Gast das meint, aber hier, an der Tabelle, da komme ich nicht weiter.
Stellenwertsystem, ein wunderbares Bild aus alten Zeiten, wahrscheinlich ein Rechentisch, wie ihn Adam Riese auch noch hatte. Präziser wäre meine Frage so: Seit wann etwa wird das perfekte und fertige Stellenwertsystem in den Schulen gelehrt? Frankfurt verbietet 1494 die Ziffern, Antwerpen verbietet sie hundert Jahre später noch. Sicherlich gingen die Mathematiker und die Physiker als erste zum indischen Rechnen mit den Ziffern über, auch Adam Riese, der beides lehrte, den Rechentisch und daneben das neue indische Verfahren. Die Buchhaltung in den Städten aber wurde noch lange mit römischen Ziffern geführt. Ich frage nach dem ungefähren Zeitpunkt, ab dem das indische Rechnen ganz allgemein im Volke, in allen Schulen, aufgrund von staatlichen Verordnungen gewissermaßen, sich vollkommen durchsetzte. Allzulange kann das noch nicht her sein, wenn man bedenkt, daß der Münzfuß Karls des Großen in Frankreich bis zur Revolution herrschte und in England bis vor ein paar Jahren noch. Wie beurteilt Ihr als Mathematiker den umstrittenen Satz des Peano von 1890, nach dem eine Zahl nur einen Vorgänger und Nachfolger haben soll (so ungefähr) - in diesem Zusammenhang. Ich denke manchmal, er könnte sozusagen den Schlußstein zum heutigen Stellenwertsystem bilden. Preußen führte um 1868 das CGS-System ein, nach französischem Vorbild wohl. Das könnte auch einen Schub für das Zehnersystem bedeutet haben, zur allgemeineren Anerkennung desselbeln beigetragen haben, stelle ich mir vor.
Falls Tycho noch mit passus rechnete, womit dann Kepler und Newton. Oder anders: In der Bibel wurden zuweilen die ältesten Maßangaben durch „neuere“ wie Finger und Ellen ersetzt, (mir fallen keine geigneteren Wörter ein), hingegen durch die allerneuesten wie Meter und Kilometer wohl noch nicht.
Gast besitzt sicher ein besseres Werk über die Geschichte der Zahlen, als jenen Wikikram.
> einsilbig - zweisilbig < dürfte so richtig wohl nicht stimmen für alle Fälle in allen Sprachen. quatre, duo, sieben und sehr viele andere Gegenbeispiele, deka, decem. Sumerisch 9 illimu
aus ia (5) + limmu (4). Opa könnte bestimmt hunderte Gegenbeispiele aufzählen, wie gotisch ainlif, ahd. einlif, nhd. elf, auch griechisch tettares 4, um diese ungewöhnliche Theorie zu widerlegen. Vielleicht fällt dem Gast etwas ein zu meiner vermutlich selbstverkorksten Tabelle der sortierten Abweichungen?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 26. März 2006 16:06 Titel: dermarkus Verfasst am: 26. März 2006 16:06 Titel: |
 |
|
Glückwunsch zum erfolgreichen Anfreunden mit dem Taschenrechner!
Opas Tabellen erscheinen mir überhaupt nicht verkorkst. Wenn man genauer hinsieht, hat auch die Abweichung des Wertes von Cambridge zugenommen, als Opa statt mit dem Sonnentag mit dem Sternentag gerechnet hat. Und weil Opa sorgfältig auch das Vorzeichen der Abweichung bei Paris mit angegeben hat, sieht man: Weil die Winkelgeschwindigkeit der Erde mit dem Sternentag größer ist als wenn man sie mit dem Sonnentag berechnet, sind auch alle damit berechneten Werte für die Coriolisablenkung größer geworden. Also passt das alles prima zueinander.
Wenn wir von exakter Erkenntnis reden, wenn wir Ergebnisse von Experimenten vorhersagen oder nachrechnen, dann müssen wir auch so exakt sein, dass wir nicht unsinnigerweise unser Rechenergebnis genauer angeben als das, was wir hineingesteckt haben. Sondern wir müssen am Ende der Rechnung unser Ergebnis sinnvoll runden.
Wie genau kennen wir die Angaben, die wir in die Formel eingesetzt haben?
Die Winkelgeschwindigkeit der Erde kennen wir nun mit dem Sternentag sehr genau.
Den Winkel der geographischen Breite kennen wir in jedem der Fälle mindestens ebenso genau wie die Fallhöhe.
Die Fallhöhe ist meist der am ungenauesten angegebene Wert.
Die gemessene Erdbeschleunigung g für Paris (g=9,809362 m/s^2) und für Bologna (g=9,804359) habe ich gefunden in einer Betrachtung der PTB Braunschweig, die sich mit der Kalibrierung von Präzisionswaagen befasst, die an unterschiedlichen Orten in Europa aufgestellt werden.
http://www.ptb.de/de/org/1/11/115/doc/gravzonen.pdf
Tabelle auf Seite 10, gemessene Werte "g_D".
(Ebenso findet sich in diesem Dokument übrigens die sogenannte WELMEC-Formel, die eine Abschätzung der Gravitationsbeschleunigung der Erde in Abhängigkeit des Breitengrades und der Höhe über dem Meer darstellt.)
Man sieht, wenn man sehr genau messen (hier: wiegen) kann, dann muss man auch sehr genau seine Messfehler korrigieren.
Wie genau die Werte waren, die Wagenschein zur Berechnung der Werte, die er angibt, verwendet hat, und wie genau die Formel war, mit der Wagenschein sie berechnet hat, das weiß ich nicht. Ich sehe nur, dass seine Werte einen sinnvollen Vergleich zu den experimentellen Werten ermöglichen, und dass er, wenn er ganz exakt hätte sein wollen (um die Kontrolle für fleißige Nachrechner zu ermöglichen), seine Rechenergebnisse mit einem Fehlerbalken versehen oder auf eine geltende Ziffer weniger gerundet hätte.
Ich erhalte mit den mir nun bekannten Daten (exakt berechnete und sinnvoll gerundete Werte):
Paris................ 8,102 mm ..... 8,1 mm
Cambridge ...... 1,789 mm .......1,8 mm
Bologna ........ 11,571 mm ..... 11,6 mm
Freiburg ........ 27,837 mm ..... 27,8 mm
Schlebusch .... 10,749 mm ..... 10,7 mm
Dabei habe ich für Paris und Bologna die oben gefundenen exakteren Werte für g verwendet, für die anderen Experimente habe ich mit 9,81 m/s^2 gerechnet.
In Paris und Cambridge ist die Angabe der Fallhöhe (zwei geltende Ziffern) für die Rundung des Ergebnisses maßgeblich, in Bologna und Schelbusch ist es die Fallhöhe (drei geltende Ziffern), und in Freiburg i.S. ist es die Erdbeschleunigung, die ich nicht besser als auf drei geltende Ziffern angeben bzw. einschätzen kann.
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 26. März 2006 22:58 Titel: Opa Verfasst am: 26. März 2006 22:58 Titel: |
 |
|
In Bologna liegt noch ein Hund begraben, von dem mir kürzlich bereits trämte. Im Traume war er ein riesig breites Vieh, so rund 444 Kilometer breit. Erst versuchte ich ihn, mit dem Atlas zu verscheuchen, jetzt aber konnte ich, dank der Liste PTB Braunschweig, ihn nahezu exakt untersuchen, äbwägen und heraustreiben.
Er flüchtete sich wieder zurück in Wagenscheins Tabelle, wo er wohl auch hingehört, wenn ich es recht bedenke, denn es könnte sich um ein, darf ich’s vermuten, pädagogisches Vieh handeln.
Erst wollte ich gar den Leuten vom Wagenschein-Archiv vom Hund in Bologna schreiben, - es könnte ja ein Druckfehlerteufelchen gewesen sein, etwas, das man bei einer Neuauflage korrigieren könnte. Jetzt aber hat Opa sich die Idee von einem pädagogisch notwendigen Bologna-Hund in den Kopf gesetzt, ein in der Natur riesenbreites, in der kleinen Tabelle aber nur winzigkleines Tierchen, von tatsächlich manchmal übersehener Art, und gerade deshalb voll tückischer, doch wohlwollend gemeinter Ersprießlichkeit. Vielleicht lebte der Hund weiland in der Nähe der Universität von Bologna, bei manchen die erste Universität des Abendlandes, ein ehrwürdiger Stern jedenfalls am Himmel der Gelehrten. Mit neuem g und neuer Hundehütte, beide aus Braunschweig geliefert, kommt Opas Sterntagrechnung jetzt auf 10,842277, richtig? Das wären dann rund 7 Zehntelmillimeterchen weniger.
|
|
 |
Gast
|
 Gast Verfasst am: 27. März 2006 03:09 Titel: Gast Verfasst am: 27. März 2006 03:09 Titel: |
 |
|
> Für Bologna gibt Wagenschein einen berechneten Wert von 11,3 an
> Phi = 40 Grad und 30 Sekunden. Fallhöhe 78,3 Meter.
> Beobachtete Abweichung 19 + - 2,5 mm, nach 16 Versuchen.
Später aber:
> Bologna40,5
Ich find für den Airport Bologna die Daten:
Höhe, 125 m ü. NN, Breite, 44°32'N, Länge 11°18'O
40°00'30" oder 40°30' oder 44°32'
Welche Breite ist die richtige?
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 27. März 2006 08:34 Titel: Opa Verfasst am: 27. März 2006 08:34 Titel: |
 |
|
Stimmt, lieber Gast, da hatte Opa zuallererst falsch abgeschrieben und aus Minuten Sekunden gemacht. Es treten diese, wenn es um Genauigkeit geht, ja schlimmen Fehler, besonders bei dem eigenen Abschreiben von Tabellen auf. Der große Gauß oder Gauss, habe ich mal gelesen, soll immer und immer wieder mit Vergnügen Tabellenwerte nachgerechnet und korrigiert haben.
Vorbildlich sachlich und nüchtern fand ich die Haltung, die hinter der Frage steht „Wie genau kennen wir die Angaben, die wir in die Formel eingesetzt haben?“ Die kann man nie oft genug stellen, anderen und sich selbst. Opa hat dann zweitens die falsche Angabe phi = 40,5 Grad ungeprüft übernommen, lange Zeit damit gerechnet und auch hierhin eingeschleppt.
Zuletzt aber übernahm er den Wert 44,50 aus der Braunschweiger Liste.
Damit, sowie mit dem verbesserten g, ebenfalls aus der Braunschweiger Liste, komme ich nun auf 10,842277 mm Ostabweichung, wenn ich diese Werte in die von euch gelernte Formel einsetze.
Solche Formeln kommen mir als mächtige Werkzeuge vor, und als ich die von euch gegebene Formel nun endlich zu beherrschen glaubte, - man kann damit ja dann in Excel ganz schnell ganz viele „Hundehütten“ oder „phi-Ställe“ und -stellen überprüfen -, da trug ich die Nase, ein paar Sekunden lang nur, um sieben Zehntelmillimeter höher.
Die Braunschweiger Liste gibt für Paris ein phi von 48,86. Mit Paris verbinde ich den Urmeter, Paris die Stadt der Genauigkeit. Sicher sind viele dorthin gereist, um den Urmeter zu kopieren.
In Wagenscheins Tabelle steht für Paris ein phi von 48 Grad, 50 Minuten Punkt 8.
(48° 50’ .8) Die 50 Minuten rechne ich um: 50 mal 1/60 Grad = 0,833 Grad. Damit ergibt sich ein phi von 48,833. Bei der Angabe Punkt 8 weiß ich nicht Bescheid. Was kann man damit noch anstellen? Sind es Sekunden, wohl kaum oder doch? Aber Kleinvieh macht auch Mist. So müßte man einen Astronomen zu Rate ziehen. Ich versuche es bei .8 mit Sekunden und setze somit noch 8/60 Sekunden ein. Nein, ich lasse sie weg, bis ich bessere Nachricht erhalte.
Das dürfte insgesamt schon eine Vergleichung ermöglichen:
alte Tabelle des W. 48,83 Grad - Braunschweiger Tabelle 48,86 Grad.
Somit sitzt im Pantheon, wo alle Götter der Freuden und Genauigkeit zusammenlaufen, nicht der riesige Bologna-Hund, sondern nur ein kleines Schoßhündchen. Die Differenz 48,86° minus 48,83° ist 3/100°. Wenn man nun geschätzt 1 Grad = 111 Kilometer nimmt, dann kommt Opa auf
3/100 von 111 Kilometer = 333/100 km = 3,33 km. Auf der Karte von Paris macht das Schoßhündchen einen Spaziergang vom Panthéon zu den Champs-Élysées, zu den himmlischen Gefilden, vielleicht zum Place de la Concorde?
Darf ich dem Gaste ein Werk empfehlen?
Karl Menninger, Zahlwort und Ziffer - Eine Kulturgeschichte der Zahl.
Es ist wohl d a s Standardwerk, mit viel Liebe geschrieben.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 27. März 2006 13:12 Titel: dermarkus Verfasst am: 27. März 2006 13:12 Titel: |
 |
|
Um ehrlich zu sein, glaube ich, dass Opa beim Berechnen der 10,8 mm für Bologna irgendwo ein Eintippfehlerlein untergekommen ist.
Ich erhalte mit den exakten Werten die 11,6 mm, wie ich sie oben angegeben habe.
Als exakte Werte verwende ich:
1 Sternentag = 86164,099 s
g in Bologna = 9,804359 m/s^2
geographische Breite der Stelle in Bologna, an der der Versuch durchgeführt wurde: 40 Grad und 30 Winkelminuten = 40,50°
Fallhöhe h = 78,3 m
Ich verwende dabei den im Wagenschein für das Experiment angegebenen Winkel für die geographische Breite, da ich den Landvermessern zur Zeit der Durchführung der Experimente sehr wohl zutraue, diesen Winkel genau bestimmt zu haben.
Außerdem ist Bologna und vor allem auch Paris eine große Stadt, deren Ausdehnung einige oder gar viele Winkelminuten beträgt (Eine Winkelminute entspricht einer Seemeile, also knapp 2 km). Wo genau innerhalb dieser Städte der Versuch stattgefunden hat, sagt mir also nicht die Tabelle der PTB, sondern die Messangaben zu den Versuchen.
Ein Fehlinterpretieren der 30 Winkelminuten aus Bologna als 30 Winkelsekunden macht einen Fehler für die Coriolisablenkung von 0,74 %, und damit fast einem Zehntelmillimeter, der sich bemerkbar macht, wenn man das Ergebnis auf drei geltende Stellen gerundet angibt.
Die Frage, wie die Winkelsekundenangaben zu interpretieren seien, kann uns für unsere Genauigkeit allerdings egal sein, da eine Winkelminute nur einen Unterschied von 0,025 % im Ergebnis bewirkt. (Ich interpretiere 48°50'.8 als 48 Grad und 50,8 Winkelminuten =( 48+(50,8/60))° )
Die Korrektur für den Sternentag ist ebenfalls ein kleiner Effekt: Das Ersetzen von 86400 s durch 86164,099 s erhöht das Ergebnis für die Coriolisablenkung nur um 0,27%.
Und das Verwenden nicht von 9,81 m/s^2, sondern des exakten gemessenen Wertes g=9,804359 m/s^2 für Bologna macht die berechnete Coriolisablenkung nur um 0,029 % größer.
Wir sehen, die Feinkorrekturen am Sternentag, an der Erdbeschleunigung und am Breitenwinkel liegen in einer viel kleineren Größenordnung (nämlich 0,1 mm bis 0,01 mm) als die 0,7 mm Unterschied, die Opa beim letzten Eintippen erhalten hat.
// edit: Das Tippfehlerchen im g korrigiert
Zuletzt bearbeitet von dermarkus am 27. März 2006 18:41, insgesamt einmal bearbeitet |
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 27. März 2006 17:09 Titel: Bologna 444 Opa Verfasst am: 27. März 2006 17:09 Titel: Bologna 444 |
 |
|
> Ich verwende dabei den im Wagenschein für das Experiment angegebenen Winkel für die geographische Breite, da ich den Landvermessern zur Zeit der Durchführung der Experimente sehr wohl zutraue, diesen Winkel genau bestimmt zu haben. <
Wagenschein schreibt: „Es dauerte über hundert Jahre, bis Newtons Anregung ... durch GUGLIELMINI im Turm Asinelli in Bologna 1791/92 ein - noch sehr fragwürdiges - Ergebnis lieferte. Seine Unzulänglichkeiten interessieren die Schüler. Es würde sich lohnen, alle Originaltexte von 1679 bis 1903 zusammenzustellen.“
- Giovanni Battista Guglielmini, noto per le importanti esperienze sulla caduta dei gravi eseguite dalla Torre degli Asinelli - (im Netz gefunden).
In der gegebenen Tabelle stand Bologna 40° 30’ für phi. Im Atlas von Diercke liegt Bologna bei 44 und einem halben Grad. In heutigen Zeiten entspricht ein Breitengrad ungefähr 111 Kilometern.
Das macht einen Unterschied von 4 Graden oder 444 km.
Wo kann der Fehler von 444 Kilometern stecken?
a) Das Gradnetz der Erde könnte vor hunderten von Jahren noch nicht so exakt festgesetzt gewesen sein wie heute. Das dürfte gewiß der Fall gewesen sein, aber nicht in der Weise, daß bei 4 Breitengraden ein Unterschied von 444 Kilometern zustande kommt. Schließlich hatte doch Eratosthenes (ca. 275 bis 195 v. Chr.), der Direktor der großen Bibliothek von Alexandria, den Erdumfang mit 39 690 Kilometern berechnet, (nach heutigen Maßangaben, Quelle G. Prause, Niemand hat Kolumbus ausgelacht). Teilen wir diesen Wert durch 360, dann läge von einem Breitengrad zum nächsten ein Abstand von 110, 25 Kilometern.
b) Es war der Druckfehlerteufel. Seit 1792 dürfte das Ergebnis von Bologna mehrfach veröffentlicht worden sein. Wagenschein zitiert seine Quelle: W. Brunner, Dreht sich die Erde? Bd 17 der „Mathematischen Bibliothek“, Teubner, Leipzig u. Berlin, 1915.
Brunner wiederum konnte ich nicht überprüfen. Es besteht die Möglichkeit, daß Brunners Quellen bereits den falschen Wert mitgeschleppt haben usw. die Quellen dieser Quellen.
c) Es handelt sich um einen pädagogischen Bologna-Hund Wagenscheins, auf den wir gestoßen sind, und dem wir mit den gefundenen Braunschweiger Werten nun auf den Leib rücken können.
Meine Rechnung benutzt jetzt die folgenden Werte:
phi 44,50 Grad; Fallhöhe 78,3 m; Sterntag 86164; g 9,804359; (dermarkus gibt noch einen zweiten Wert für g „9,04359“, ein Tippfehlerchen?)
Mit diesen eingesetzten Werten, bei g zweimal 9,804359, liefert die Formel bei mir 10,8422774 mm Ostabweichung. Ist die Formel richtig angewandt?
| Beschreibung: |
|
| Dateigröße: |
16.81 KB |
| Angeschaut: |
16221 mal |

|
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 27. März 2006 18:47 Titel: dermarkus Verfasst am: 27. März 2006 18:47 Titel: |
 |
|
In der Tat, ein Tippfehlerchen meinerseits beim g. Ich hab es gleich oben korrigiert.
Jetzt verstehe ich das! An so eine Riesenabweichung im Breitengradwinkel hatte ich nie und nimmer gedacht! Mein Diercke-Atlas sagt dasselbe wie Opas, und der Torre Asinelli steht in der Tat in dem Bologna, von dem wir sprechen. Ich bin für die Erklärung b) (Druckfehlerteufel), und ich bin einverstanden, dass die Korrektur nun, wie Opa sagt, einen deutlich kleineren Wert für die berechnete Coriolisablenkung ergibt! (Mein Taschenrechner sagt 10,8506 mm, wenn ich Opas letztgenannte Werte einsetze.)
|
|
 |
Gast
|
 Gast Verfasst am: 28. März 2006 02:08 Titel: Gast Verfasst am: 28. März 2006 02:08 Titel: |
 |
|
> Mein Taschenrechner sagt 10,8506 mm ..
Mein Bildschirm-Rechner auch, hier sind die Rohdaten (copy) zum Vergleich für Opa:
sc = cos(b)*(1/3)*w*g*(2*h/g)^(3/2)
h = 78.3 m
b = 44.5°
g = 9.804359 m/s^2
w = 7.292115138556241e-5 1/s (wsid, entspricht 2pi/86164.099)
sc = 1.085056493712043e-2 m = 10,85 mm
Wenn g nicht verfügbar sein sollte dann hilft die 'amtliche' Gleichung
g = 9,780318*(1 + 5.3024e-3*sin^2(b) - 5.8e-6*sin^2(2*b)) - 3.085e-6*a
mit b = geogr. Breite und a = Höhe über NN (e steht für 10^, z.B. e-3 = 10^-3).
Für Bologna 44.5° und a = 125 m liefert sie g = 9.805352711962246e+0.
Mit diesem Wert wird sc = 1.085001510430531e-2 m; ich denke 10,85 mm
darf nunmehr als korrekter Wert beschlossen und verkündet werden.
Eigentlich ein schönes Javascript-Projekt, man müsste nur noch
h und b eintippen (g nur wenn vorhanden) und auf CALC drücken..
-------
Wieder zurück zum Ursprungsthema, der rätselhaften Gravitation.
Opa hat Descartes erwähnt mit seiner Vermutung, die Ursache sei 'draußen' zu finden
und nicht drinnen, in der Materie. Ist das bei Wagenschein weiter ausgeführt oder nur
als zwar exotische aber längst vertrocknete Blüte des Denkens vermerkt?
Ich frage deshalb, weil ich gerade ein Buch lese, in dem eine solche Theorie entwickelt
wird, in der Tradition von LeSage, aber in modernerem Gewand. Der alte Aether tritt auch
wieder auf, aber nicht als materieller mit unvereinbaren Eigenschaften, sondern als eine
Erscheinungsform des lokalen Gravitationspotentials. Und das GPS wird benutzt als eine
riesige und extrem präzise Version des Michelson-Morley Experiments. Spannend bis jetzt..
does gravity push or pull? -- it sucks! (Aufdruck auf einem T-Shirt)
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 28. März 2006 03:00 Titel: Bologna-Hund erlegt Opa Verfasst am: 28. März 2006 03:00 Titel: Bologna-Hund erlegt |
 |
|
> Mein Taschenrechner sagt 10,8506 mm <
Das fand ich sehr befriedigend, denn mein Taschenrechner sagt auch 10,8506mm. Von Excel stammte 10,8422774. Falsch, es stammte von mir, ich hatte den Inhalt aus einer falschen Zelle herüberkopiert. Seh ich erst jetzt, tut mir leid. Da sehe ich wieder, wo man doch überall Fehler machen kann, und dann trotzdem meint, es sei richtig. Jetzt sehe ich den richtigen Wert 10,850577 in der Zelle daneben stehen. Drei Anläufe mit dem Windowsrechner mußte ich machen, bis ich meinen Kopierfehler dann endlich doch noch fand.
> und ich bin einverstanden, dass die Korrektur nun, wie Opa sagt, einen deutlich kleineren Wert für die berechnete Coriolisablenkung ergibt! <
Wenn ich wüßte, was eine Coriolisablenkung sei, dann wäre mir wohler. Bislang benutzte ich den mir verständlicheren Ausdruck Ostabweichung, die ja beobachtet wurde, und die wir mit Hilfe geheimnisvoller Formeln berechnet haben.
Merkwürdigerweise wurde Coriolis im Jahre 1792 geboren, als in Bologna die Versuche am Asinelliturm stattfanden, 113 Jahre nach Newtons Vorschlag. Die weiteren Versuche, Benzenberg 1802 zu Hamburg innerhalb des Michaelisturms, Benzenberg 1804 im Kohlenschacht zu Schlebusch, heute gehört der Ort wohl zu Leverkusen, dann Reich 1831 zu Freiburg in Schlesien, - die liegen alle vor der Zeit der „Coriolisablenkung“. Also bleibe ich aus historischen Gründen besser bei dem Ausdruck Ostabweichung. Denn es geht doch um die Frage, ob die Erde sich dreht, und ob Kindern der Volksschule bzw. Hauptschule dieses klar und verständlich vermittelt werden kann, ob also eine beobachtete Ostabweichung einen Beweis für das Herumdrehen der Erde ist, sobald man mit Galilei und Newton an die „Trägheit“ glaubt, was ja schon schwer genug zu verstehen ist. Gleichwohl ist Opa neugierig, ob in unserer Formelrechnerei ein Corioliseffekt schon drinsteckte und ob die Physiker in ihrem Sprachgebrauch überhaupt Ostabweichung mit Coriolisablenkung gleichsetzen?
Ich setze noch ein gif in den Anhang.
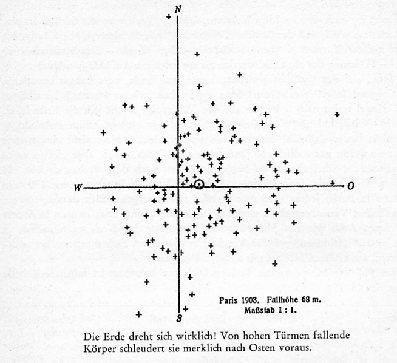
Das Bild mußte um etwa dreißig Prozent verkleinert werden, erscheint also nur fast im Maßstab 1:1. Die 144 kleinen polierten Stahlkugeln im Panthéon fielen anscheinend alle auf eine Fläche, die einem halben Blatt Papier entspricht. Und das als ein Beweis für die Umdrehung der riesigen Erde. Zugleich sieht man, wie durch viele Wiederholungen ein Versuchsergebnis zustandekommt.
Unten steht Wagenscheins zusammenfassender Satz:
Die Erde dreht sich wirklich! Von hohen Türmen fallende
Körper schleudert sie merklich nach Osten voraus.
| Beschreibung: |
|
| Dateigröße: |
77.12 KB |
| Angeschaut: |
16173 mal |
|
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 28. März 2006 05:21 Titel: Opa Verfasst am: 28. März 2006 05:21 Titel: |
 |
|
Edler Gast, nun sind wir, glaube ich, auf dem Place de la Concorde angelangt. Ich habe viel hier lernen können.
Wagenschein erwähnt den Descartes auf den ersten Blick nur kurz in einer Fußnote. Die ganze Arbeit heißt „Die Erfahrung des Erdballs“. Vielleicht suchst Du mal nach dem Wagenschein-Archiv per Google. Ich meine, gesehen zu haben, daß einige Aufsätze als PDF zur Verfügung stehen.
Wenn auch der genannte Titel darunter ist, dann sollte man auf das Nachwort 1970 achten. Denn dann wäre es die vollständige Fassung der Arbeit, wie sie zuletzt bei Klett veröffentlicht wurde, aus der ich zitiert habe. In meinem Buch umfaßt der Abdruck ca. 32 Seiten.
Menninger kanntest Du schon? Ein absolutes Muß für jeden Mathematiker und Historiker. Es gibt da nichts Besseres auf dieser Welt, ein Nachschlagewerk fürs ganze Leben. (Letzter Nachdruck 1989, dürfte in Leinen rund fünfzig E kosten). Mein Rat, ehe es wieder für Jahrzehnte vergriffen ist, ...
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 28. März 2006 12:19 Titel: dermarkus Verfasst am: 28. März 2006 12:19 Titel: |
 |
|
Mit Coriolisablenkung meine ich in der Tat genau dasselbe wie die Ostabweichung. Denn ich habe die oben verwendete Formel für die Größe der Ostabweichung mit der Formel für die Corioliskraft im rotierenden Bezugssystem hergeleitet. Und damit ausgerechnet, um welche Strecke s_c der fallende Körper vom Lot horizontal nach Osten abweicht, weil sich die Erde dreht.
Also : s_c = Coriolisablenkung = Ostabweichung = Abstand vom Lotpunkt zum ein bisschen weiter östlich gelegenen tatsächlichen Auftreffpunkt.
Weil also Coriolis eine so schöne elegante theoretische Beschreibung dieses Phänomens gefunden hat, kennt man diesen Effekt heute unter seinem Namen, auch wenn ihn schon andere vor ihm gemessen und beschrieben haben.
|
|
 |
Gast
|
 Gast Verfasst am: 28. März 2006 14:32 Titel: Gast Verfasst am: 28. März 2006 14:32 Titel: |
 |
|
Dank an Opa für die Literaturhinweise, das Wagenschein-Archiv habe ich gefunden und dort auch "Die Erfahrung des Erdballs", samt Nachwort von 1970, dazu noch "Die Erde unter den Sternen" sowie "Zusammenhänge der Naturkräfte", also erstmal genug Stoff zu verdauen.
Die 'Ostabweichung' die wir hier zum Thema hatten ist in der Tat nur ein Teilaspekt des nach Coriolis benannten Effekts, der eigentlich dreidimensional ist, und auch bei Bewegungen entlang der Erdoberfläche zur Ablenkung der Bewegung führt. Ein Beispiel dafür ist etwa die Ablenkung von Luft- oder von Wasserströmungen. Das Bild unten zeigt einen solchen Fall in der Bewegung von treibenden Bojen, es stammt aus dem schon erwähnten Papier von Anders Persson 'The Coriolis Effect – a conflict between common sense and mathematics', dessen Lektüre mir, zusammen mit Markus' dankenswerten Ausführungen, sehr dabei geholfen hat, mich von der 'flache Erde' Vorstellung zu verabschieden, die übrigens auch Wagenschein, zumindest explizit, nicht überwindet bei seiner Darstellung der Ostabweichung. Allerdings geht es ihm auch nur um die qualitative Begründung, und dafür genügt der intuitiv leicht erfassbare Geschwindigkeitsunterschied zwischen 'oben' und 'unten' oder 'außen' und 'innen' von dem ich zunächst auch ausging. Aber es steckt wesentlich mehr dahinter. Ganz kurz gesagt, der Coriolis-Effekt sorgt für eine Ablenkung, die stets senkrecht sowohl zur Drehachse des rotierenden Bezugssystems als auch zur Richtung der Bewegung zeigt. Als eine Scheinkraft ändert die Coriolis-Kraft niemals den Betrag der Geschwindigkeit der abgelenkten Masse (also seine Bewegungsenergie), sondern allein die Richtung. Die Folge davon ist die Bewegung auf einer Kreisbahn, was im Bild sehr schön zu erkennen ist. Da es sich um einen Trägheitseffekt handelt könnte man auch sagen, er sorgt dafür, dass die Dinge da zu bleiben versuchen, wo sie schon sind, in diesem Fall aber auf sehr dynamische Weise.
| Beschreibung: |
|

Download |
| Dateiname: |
inertia_circle.jpg |
| Dateigröße: |
54 KB |
| Heruntergeladen: |
7157 mal |
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 29. März 2006 22:31 Titel: anderer Blickwinkel Opa Verfasst am: 29. März 2006 22:31 Titel: anderer Blickwinkel |
 |
|
Unten im Bild, aus einem anderen Blickwinkel, die beiden Türme. Torre degli Asinelli erscheint so auch etwas größer.
Aus einem alten Lexikon, mit dem auch mir neuen Kanonenversuch:
„Ein Haupteinwand, der gegen die Rotation der E. erhoben wurde, namentlich von Tycho Brahe und Riccioli, war der, daß bei einer Drehung der E. um ihre Achse ein frei fallender Körper nicht senkrecht unter seinem Ausgangspunkt, sondern westlich von demselben auf die E. kommen müßte, weil die letztere während des Falles sich ein Stück nach O. drehe. Bei Fallversuchen, die Riccioli 1640 an einem Turm zu Bologna anstellte, hatte er von einer solchen Abweichung nichts wahrnehmen können.
Auch Mersenne und Montier stellten darauf bezügliche Versuche an, indem sie aus senkrecht in die E. gegrabenen Kanonen Kugeln abschossen, die aber, wie nicht anders zu erwarten, keinerlei Entscheidung lieferten.
Der ganze Einwand ist indessen falsch, wie zuerst Newton zeigte. Denn wenn aus dem höher liegenden Punkt ein Körper herabfällt, so behält er die seinem Ausgangspunkt entsprechende größere Geschwindigkeit während des Falles bei, er eilt daher dem senkrecht unter dem Ausgangspunkt liegenden Punkte der E. in der Richtung nach O. voraus, und er muß also nicht westlich, sondern weiter östlich auf die E. fallen. Die zur Prüfung dieser Theorie von Hooke angestellten Versuche blieben freilich erfolglos, weil die gewählte Fallhöhe von 27 Fuß zu klein war, und ebensowenig Erfolg hatten die 1791 von Gulielmini in einem Turm zu Bologna angestellten Versuche. Aber 1802 wiederholte Benzenberg diese Versuche am Michaelisturm zu Hamburg bei 235 Fuß und 1804 in einem Kohlenschacht bei Schlebusch in der Grafschaft Mark bei 262 Fuß Fallhöhe. Am erstern Ort erhielt er 4,3, am letztern 5,1 Linien Abweichung, während Gauß 4,0 und 4,6 berechnete. Versuche endlich, welche Reich 1831 im Dreibrüderschacht bei Freiberg bei 488 Fuß Fallhöhe ausführte, ergaben 12,6 Linien Abweichung nach O. Die Theorie verlangt übrigens auch eine äußerst unbedeutende Abweichung nach S.“
Fehler ???
1) Gulielmini, 2) am Michaelisturm, 3) Reich 1831 im Dreibrüderschacht bei Freiberg;
1) W.: Guglielmini mit g, 2) W.: im Michaelisturm;
3) W.: Freiburg i. S.
http://www.geophys.tu-bs.de/geschichte/reich.html
Freiburg in Schlesien oder Freiberg in Sachsen, bisher haben wir mit 50 Grad und 33 Minuten gerechnet. Müssen wir das jetzt ändern? Nicht, daß wir wieder mit womöglich 444 km Unterschied rechnen.
Zugleich eröffnet sich die Gelegenheit, einen ausgewiesenen Rechner, den größten Mathematiker aller Zeiten sogar, zu Rate zu ziehen. Leider gibt er (nach Meyers Konv. Lexikon im Netz) keine Millimeter an, sondern Linien (und wohl auch Füße).
Über Coriolis muß ich noch lernen, zumal bei manchen Artikeln im Netz doch schon noch das Wort Ostabweichung im Gebrauche ist.
Im Anfang der Nachprüfung der Tabelle von W., da gab es auch den Ansatz, wenn ich mich nicht irre, die „Herumschleudergeschwindigkeiten“ vom Erdboden und vom Turm (Asinelli) getrennt voneinander zu berechnen. Wenn man die Fallhöhe zu 78,3 Metern hat, den Breitengrad zu 44,5 hat, den Wert für g zu 9,804359 hat, die Erdzeit in Sekunden (24 mal 60 mal 60) festsetzt, dann scheint nur noch der Radius der Erde zu fehlen. In welcher Größe wollen wir diesen nun festsetzen, damit man die beiden Aufgaben gemeinsam rechnen kann?
Also mal ohne Corioliseffekt, denn da müßte doch auch etwas herauskommen. Dann könnte man vielleicht mit Gaußens Linien in den anderen Fällen, Schlebusch und Hamburg, vergleichen, vorausgesetzt, man wüßte, was ein Fuß und was eine Linie denn sind, oder aber man könnte deren Maßverhältnis erschließen aus den Rechnungen oder aus den alten Angaben des alten Lexikons.
Gauß, 30. 4. 1777 - 23. 2. 1855, hat ja von Coriolis, 1792 bis 1843, durchaus wissen können. Wenn wir also aus beiden Blickwinkeln vorgehen, einmal ohne und einmal mit Coriolis, dann können wir vielleicht auch ungefähr sehen, ob Gauß die Coriolisablenkung mitverechnet hat, oder nicht?
| Beschreibung: |
|
| Dateigröße: |
55.7 KB |
| Angeschaut: |
16592 mal |

|
|
|
 |
Gast
|
 Gast Verfasst am: 30. März 2006 02:45 Titel: Gast Verfasst am: 30. März 2006 02:45 Titel: |
 |
|
> Die Theorie verlangt übrigens auch eine äußerst unbedeutende Abweichung nach S.
Das ist der Tat richtig, ich verweise auf die knappe Beschreibung des Coriolis-Effekts in meinem vorigen Beitrag. Sie ist eine Folge der ostwärtigen Ablenkung die aus der Abwärtsbewegung resultiert. Im Bild unten ist eine Tabelle, in der die Bewegungen und Ablenkungen in drei Richtungen qualitativ dargestellt sind. Die Ostabweichung ist nur eine Komponente, sie ist in der rechten Spalte zu finden. Eine Bewegung in Richtung Osten hat ein Ablenkung in zwei Richtungen zur Folge, einmal südwärts (in der Tabelle als 'Nordwärts -1') und gleichzeitig auch aufwärts ('Abwärts -1'). Für die Südablenkung ist allerdings der Sinus der Breite als Faktor im Spiel, dieser Effekt ist am Äquator null, während die Ostablenkung dort maximal ist. Durch diese komplexe Dynamik kommt die im letzten Beitrag gezeigte Schleifenbahn der treibenden Bojen zustande, was als Trägheitskreis bezeichnet wird.
Als Merkhilfe für die Richtung der Ablenkung kann man die für solche Zusammenhänge gern verwendete Drei-Finger-Regel benutzen, auch UVW-Regel genannt, weil sie Ursache, Vermittelung und Wirkung verknüft. Hält man Daumen, Zeigefinger und Mittelfinger der rechten Hand senkrecht zueinander dann zeigt der Daumen in Richtung der Bewegung (weg von der Achse), der Zeigefinger nach oben (Rotation, Erdachse, Norden) und der Mittelfinger zeigt in Richtung der Ablenkung (Westen). Bei einer Bewegung entgegen der Richtung des Daumens (dann abwärts, in Richtung Achse, Fall) zeigt die Ablenkung dann auch entgegengesetzt zur Richtung des Mittelfinger, also Osten. Ich wünsche ein fröhliches Fingerbiegen, das hält die Gelenke in Form ;-) man kann sich das aber auch aufzeichnen.
Das Ergebnis der Ostabweichung bei alleiniger Betrachtung der unterschiedlichen Geschwindigkeiten (oben schneller als unten) steht zur wirklichen Ablenkung im Verhältnis 3:2, das hatte ich früher schon ausgeführt und mit einem Bild zu Galileis 'flache Erde' Näherung illustriert. Die Gleichung dafür ist s=cos(b)*w*h*Wurzel(2*h/g), den Erdradius braucht man dafür nicht, weil nur die Differenz der Bahngeschwindigkeiten bei Radius 'oben' (w*ro) und 'unten' (w*ru) auftritt, ro-ru ist aber die Fallhöhe h, daher kommt das Produkt w*h in der genannten Gleichung, die nichts weiter ist als die Beschreibung der Weite eines horizontalen Wurfs. Zusätzlich ist noch g, die Breite und die Winkelgeschwindigkeit der Erde w nötig. Das korrekte Ergebnis erhält man durch Multiplikation des so gefundenen Werts mit 2/3.
| Beschreibung: |
|
| Dateigröße: |
9.09 KB |
| Angeschaut: |
16577 mal |
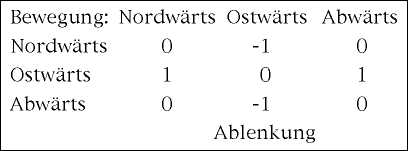
|
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. März 2006 13:08 Titel: Re: anderer Blickwinkel dermarkus Verfasst am: 30. März 2006 13:08 Titel: Re: anderer Blickwinkel |
 |
|
zu den "Fehlern":
1) Ich halte die italienische Schreibweise "Guglielmini" für richtig.
2) kann ich nicht beurteilen, ich war noch nicht im oder am Michaelisturm
3) hier erscheint mir Freiberg in Sachsen glaubhafter, da die Quelle, die Opa gefunden hat, mehr Details zu kennen scheint als Wagenschein.
Zum Minieffekt Südabweichung: In der Tat erfährt der fallende Körper auch eine Südabweichung. (Dies gilt allerdings nur auf der Nordhalbkugel der Erde, auf der Südhalbkugel wäre es umgekehrt.) Und in der Tat ist diese Südabweichung sehr, sehr klein, nämlich prozentual etwa um soviel kleiner als die Ostabweichung, wie die Ostabweichung kleiner als die Fallhöhe ist.
Da die Rechnungen von Gauß sehr gut mit den Messergebnissen übereinstimmen, wird er die Ostabweichung korrekt berechnet haben, (wenn er gerechnet hätte wie Galilei, dann wäre sein Ergebnis um die Hälfte zu groß gewesen, wie Gast richtig erklärt hatte). Das spricht dafür, dass man die Umrechnung von Fuß in Meter und die Umrechnung von mm in Linien herausfinden kann, wenn man den korrekten Breitengrad des Versuchsortes kennt  und die Angaben zu Gaußs Ergebnissen mit den Berechnungen mit unserer oben verwendeten Formel vergleicht. und die Angaben zu Gaußs Ergebnissen mit den Berechnungen mit unserer oben verwendeten Formel vergleicht.
Zuletzt bearbeitet von dermarkus am 30. März 2006 15:33, insgesamt 2-mal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. März 2006 13:29 Titel: dermarkus Verfasst am: 30. März 2006 13:29 Titel: |
 |
|
Zur Verwendung der Dreifingerregel, die Gast beschreibt, möchte ich Verwirrungen vorbeugen. Das Prinzip "Ursache, Vermittlung, Wirkung" ist eine Merkregel, die hier für mein Gefühl nur zufällig zum richtigen Ergebnis geführt hat.
Die Corioliskraft ist
)
Das Kreuzprodukt bildet ein Rechtssystem.
Die Richtung des Vektors, der das Kreuzprodukt von omega und v ist, ermittelt man also folgendermaßen mit der Dreifingerregel der rechten Hand:
Der rechte Daumen zeigt in Richtung der Drehachse der Erde (die zeigt von Süd nach Nord), der rechte Zeigefinger zeigt in Richtung der Geschwindigkeit v; dann zeigt der rechte Mittelfinger (senkrecht zur von den Vektoren omega und v aufgespannten Ebene) in die Richtung des Kreuzproduktes von omega mit v.
Da die Corioliskraft wegen dem Minuszeichen in der Formel in die entgegengesetzte Richtung dieses Kreuzproduktes zeigt, muss man die Richtung des erhaltenen Vektors dann noch invertieren. Statt dessen kann man in diesem Fall komplett die Dreifingerregel der linken Hand nehmen, um dieses Minuszeichen zu berücksichtigen:
Also: zeigt der linke Daumen in Richtung der Drehachse der Erde und der linke Zeigefinger in Richtung der Geschwindigkeit des Körpers, dann zeigt der linke Mittelfinger in die Richtung der Corioliskraft (senkrecht zu diesen beiden Vektoren) auf diesen Körper.
----------------------------------
Wendet man dies auf der Nordhalbkugel an, (dort entspricht eine Bewegung nach Norden einer Annäherung an die Erdachse) dann sieht man zusätzlich zu dem, was wir schon wissen, dass eine Bewegung in östliche Richtung eine Corioliskraft nach Süden bedeutet, und dass eine Bewegung in westlicher Richtung eine Corioliskraft nach Norden bedeutet.
Ebenso gibt es für eine Bewegung nach Norden eine Corioliskraft nach Osten, und für eine Bewegung nach Süden eine Corioliskraft nach Westen.
Dies stimmt mit Gasts Bild für die Bojenbewegung in der Ostsee überein, und erklärt nun auch anschaulich, warum einer der ersten experimentellen Hinweise auf die Existenz der Corioliskraft die Tatsache gewesen sein kann, dass Kanoniere feststellten, dass ihre Kanonenkugeln aus einem seltsamen, ihnen unerfindlichen Grund ihr Ziel verfehlten, obwohl sie es richtig anvisiert hatten.
|
|
 |
Gast
|
 Gast Verfasst am: 30. März 2006 19:07 Titel: Gast Verfasst am: 30. März 2006 19:07 Titel: |
 |
|
Einverstanden, Daumen rauf, das ist auch eine wesentlich angenehmere Position.
Die Sachen klären, die Hand entspannen, frei nach Hentig.
Hier ist ein, wie ich finde, erstaunliches Experiment von Geoffrey Ingram Taylor. Links im Bild wird ein tropfen Tinte in ruhendes Wasser getropft und verteilt sich in Form einer Wolke wie man das erwarten würde. Rechts rotiert der Behälter samt Wasser, und die nahe dem Rand eingetropfte Tinte bildet jetzt eine senkrechte Säule, denn nur die Bewegung parallel zur Drehachse führt nicht zu einer Ablenkung durch den Coriolis-Effekt.
| Beschreibung: |
|

Download |
| Dateiname: |
taylor-coriolis.jpg |
| Dateigröße: |
19.16 KB |
| Heruntergeladen: |
7928 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. März 2006 20:12 Titel: dermarkus Verfasst am: 30. März 2006 20:12 Titel: |
 |
|
Und jede Bewegung senkrecht zur Drehachse führt zu einer Corioliskraft und damit zu einer Kreisbewegung der Tinte, und damit kommt die Tinte senkrecht zur Drehachse nicht weit, sondern kreiselt dort, wo sie ist.
Ein schönes Experiment! 
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 30. März 2006 21:08 Titel: Opa Verfasst am: 30. März 2006 21:08 Titel: |
 |
|
Drei Fragen
> Die Gleichung dafür ist s=cos(b)*w*h*Wurzel(2*h/g), den Erdradius braucht man dafür nicht, weil nur die Differenz der Bahngeschwindigkeiten bei Radius 'oben' (w*ro) und 'unten' (w*ru) auftritt, ...<
Opa meint, doch den Erdradius benutzen zu müssen, da ja sonst die ganze Erde ihm zu verschwinden droht. Wenn er mit Kosinus rechnet, dann entspricht - nach dem Satz Kosinus (alpha) = Ankathete zu Hypotenuse - die Hypotenuse dem Erdradius.
Daraus folgt für mich, der Erdradius ist in diesen Formeln allgegenwärtig.
> Die 'flache Erde' Vereinfachung liefert s=w*h*Wurzel(2*h/g), aber die 'rückwärts' gerichtete Beschleunigung nimmt 1/3 davon wieder weg, .. <
Also, habe ich daraus geschlossen, beträgt die Ostabweichung ohne Coriolis 3 Drittel, und die Coriolisablenkung nimmt ungefähr1/3 davon dann weg. Demnach bleiben rund 2 Drittel der oben am Turm schnelleren Bewegung erhalten, was sich dann am Erdboden in Millimetern nachmessen ließ.
(1) Ist das so richtig ausgedrückt?
(2) Falls ja, dann bleibt die Frage nach einem Namen für das ursprüngliche 3/3, jetzt nur noch 2/3??
Ich möchte noch zu fragen wagen, in welchem Alter ein Schüler heute den Kosinussatz kennen lernt. Zu meinen Schulzeiten war das in U II, im Alter von 16 Jahren.
In der Volksschule gab es überhaupt keinen Sinus oder Kosinus. Stellt Gast sich vielleicht vor, daß man den jüngeren Kindern, den 13-, 14- und 15jährigen nun nichts über den Erdball sagen darf, ganz im Gegensatz zu Wagenschein? Der schrieb: „Annähernd Wahres verstehen ist besser, als ganz Wahres unverstanden nachreden.“ (Quelle: Wagenschein, Die pädagogische Dimension der Physik, 1971, S. 272).
(3) Geht es hier in diesem Forum nicht auch um pädagogische Dimensionen???
Gruß an Gast und Markus
|
|
 |
|
|

















 ) Ich bin auch einverstanden mit den Werten 1,3 cm für 100 m Fall und 2,7 mm für 25 m Fall.
) Ich bin auch einverstanden mit den Werten 1,3 cm für 100 m Fall und 2,7 mm für 25 m Fall.





