| Autor |
Nachricht |
koppi89
Anmeldungsdatum: 03.03.2006
Beiträge: 15
|
 koppi89 Verfasst am: 03. März 2006 15:48 Titel: Gewicht eines Körpers in Abhängigkeit von der Höhe koppi89 Verfasst am: 03. März 2006 15:48 Titel: Gewicht eines Körpers in Abhängigkeit von der Höhe |
 |
|
 Kann mir bitte jemand helfen? Kann mir bitte jemand helfen? 
Ich muss eine genaue Erklärung abgeben, ob ein Körper auf dem Mount Everest (beziehungsweise in großer Höhe wie z.B. 8000m) leichter oder schwerer ist als auf der Erde?
Mittlerweile weiß ich, dass man minimal leichter ist (oder stimmt`s doch nicht?)
ABER: 
Ich weiß nicht warum das so ist? Und genau das muss ich erklären?
Kann das mit dem Druck und der Auftriebskraft zusammenhängen?
Was bitte verstehst du unter einem Titel? HHHIIILLLFFEEE ist doch wohl das Schlechteste was du aussuchen konntest, oder? Denk doch vielleicht 10 Sekunden nach.
|
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 03. März 2006 15:56 Titel: Nikolas Verfasst am: 03. März 2006 15:56 Titel: |
 |
|
Der Körper wird durch die Gewichtskraft nach unten gezogen. Wahrscheinlich kennst du die Gleichung für die Gewichtskraft, oder? (Wenn nicht, Wikipedia)
[Ich meine nicht die Näherung F=m*g]
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. März 2006 16:45 Titel: dermarkus Verfasst am: 03. März 2006 16:45 Titel: |
 |
|
Das hat nichts mit Druck oder Auftriebskraft zu tun.
Es gibt hier allerdings zwei andere Effekte:
Zum einen nimmt die Stärke der Gewichtskraft mit zunehmendem Abstand vom Erdmittelpunkt ab.
Und zum anderen nimmt die Gewichtskraft zu, weil sich unter dem Gipfel des Mount Everest ein Gebirge mit einer Masse befindet, das eine zusätzliche Schwerkraft erzeugt.
Jeder Effekt für sich, so schätze ich, verändert die Gewichtskraft um mehr als ein Promille, und die spannende Aufgabe wird sein, abzuschätzen, welcher der beiden Effekte größer ist, und ob sich also die Erdbeschleunigung auf dem Mount Everest vergrößert oder verkleinert gegenüber der auf Meeresniveau.
|
|
 |
koppi89
Anmeldungsdatum: 03.03.2006
Beiträge: 15
|
 koppi89 Verfasst am: 03. März 2006 16:51 Titel: koppi89 Verfasst am: 03. März 2006 16:51 Titel: |
 |
|
Dankeschön!!!!!
Wenn die Fragestellung lautet:
in größeren Höhen nimt einerseits die dichte der luft ab, was zu geringerem auftrieb führt; andererseits nimmt aber auch die fallbeschleunigung ab, was zu einer gewichtsverringerung führt;
gleichen sich diese Effekte gegenseitig aus?
die Hilfestellung dabei lautet:
F = m*g - roh (dichte) * g *V
= F(h) = m * g(h) - roh (h) * g(h) *V
= g* (m - roh * V)
wobei roh * V die masse der verdrängten luft ist
welche antwort könnte ich da geben?
|
|
 |
Gast
|
 Gast Verfasst am: 03. März 2006 17:02 Titel: Gast Verfasst am: 03. März 2006 17:02 Titel: |
 |
|
Die Hilfestellung ist dabei eher verwirrend, da diese impliziert, dass die Fallbeschleunigung konstant ist.
Inwiefern sich das ausgleicht, kann ich dir nicht sagen, aber du kannst es ja mal ausrechnen.
Für die Dichte der Luft in Abhängigkeit der Höhe musst du die barometrische Höhenformel anwenden.
|
|
 |
koppi89
Anmeldungsdatum: 03.03.2006
Beiträge: 15
|
 koppi89 Verfasst am: 03. März 2006 17:13 Titel: dankeschön koppi89 Verfasst am: 03. März 2006 17:13 Titel: dankeschön |
 |
|
|
welche antwort kann ich da geben: auf die frage warum man leichter/schwerer wird?????
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. März 2006 17:27 Titel: dermarkus Verfasst am: 03. März 2006 17:27 Titel: |
 |
|
| koppi89 hat Folgendes geschrieben: |
Wenn die Fragestellung lautet:
in größeren Höhen nimt einerseits die dichte der luft ab, was zu geringerem auftrieb führt; andererseits nimmt aber auch die fallbeschleunigung ab, was zu einer gewichtsverringerung führt;
gleichen sich diese Effekte gegenseitig aus?
die Hilfestellung dabei lautet:
F = m*g - roh (dichte) * g *V
= F(h) = m * g(h) - roh (h) * g(h) *V
= g* (m - roh * V)
wobei roh * V die masse der verdrängten luft ist
welche antwort könnte ich da geben? |
Die Antwort auf die Frage "Gleichen sich die Effekte gegenseitig aus" ist "Nein", denn wie man der Formel ansieht, wirkt sich eine Veränderung von g gleich auf Gewichtskraft und Auftriebskraft aus, also ist alleine der Luftdruck entscheidend, und der Auftrieb ist dort oben kleiner.
Im übrigen bin ich der Meinung, dass die Gravitationsbeschleunigung da oben größer ist als normal (weil der Effekt durch die Gebirgsmassen größer ist als der durch den etwas größeren Abstand vom Erdmittelpunkt.)
Zuletzt bearbeitet von dermarkus am 03. März 2006 17:29, insgesamt einmal bearbeitet |
|
 |
koppi89
Anmeldungsdatum: 03.03.2006
Beiträge: 15
|
 koppi89 Verfasst am: 03. März 2006 17:29 Titel: super danke koppi89 Verfasst am: 03. März 2006 17:29 Titel: super danke |
 |
|
super danke!
aber was für eine antwort bzw. erklärung, die leicht verständlich ist, kann ich geben; warum man leichter wird?????????
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. März 2006 17:30 Titel: dermarkus Verfasst am: 03. März 2006 17:30 Titel: |
 |
|
|
Man wird nicht leichter, man wird sogar ein bisschen schwerer! Weil unten dran zusätzlich das Gebirge an einem zieht!
|
|
 |
koppi89
Anmeldungsdatum: 03.03.2006
Beiträge: 15
|
 koppi89 Verfasst am: 03. März 2006 17:32 Titel: koppi89 Verfasst am: 03. März 2006 17:32 Titel: |
 |
|
oje, jetz kenn ich mich aber nicht mehr aus?
wie kann man das erklären???????
womit hängt das zusammen??????
|
|
 |
koppi89
Anmeldungsdatum: 03.03.2006
Beiträge: 15
|
 koppi89 Verfasst am: 03. März 2006 17:51 Titel: koppi89 Verfasst am: 03. März 2006 17:51 Titel: |
 |
|
ich habe grad wieder gelesen, dass man um einen kleinen prozentsatz leichter wird!!!
warum?????????????????????????????????????
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. März 2006 17:51 Titel: dermarkus Verfasst am: 03. März 2006 17:51 Titel: |
 |
|
| koppi89 hat Folgendes geschrieben: | oje, jetz kenn ich mich aber nicht mehr aus?
wie kann man das erklären???????
womit hängt das zusammen?????? |
Das ist einfach die Massenanziehungskraft. Zwei Massen ziehen sich gegenseitig an. Genauso wie der Planet Erde mit seinem großen Gewicht im großen Abstand von ca. 6400 km vom Schwerpunkt an dir zieht, so zieht auch das Gebirge mit einer viel kleineren Masse, dafür mit einem viel kleineren Abstand vom Schwerpunkt (vielleicht 4 km) auch ein bisschen an dir.
Aber für die Erklärung deiner Aufgabe brauchst du das nicht. Da reicht es zu sagen, die Auftriebskraft auf einen Ballon wird kleiner, weil der Luftdruck kleiner wird.
(Denn g wirkt gleich auf Luft und Ballon, also macht eine Veränderung von g, egal ob es nun größer oder kleiner wird, keinen Unterschied.)
Zuletzt bearbeitet von dermarkus am 03. März 2006 21:42, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. März 2006 17:52 Titel: dermarkus Verfasst am: 03. März 2006 17:52 Titel: |
 |
|
|
Diejenigen, die schreiben, dass man da oben leichter wird, beschreiben den Effekt, dass die Schwerkraft der Erde abnimmt, je weiter du dich von ihr entfernst.
|
|
 |
koppi89
Anmeldungsdatum: 03.03.2006
Beiträge: 15
|
 koppi89 Verfasst am: 03. März 2006 17:53 Titel: koppi89 Verfasst am: 03. März 2006 17:53 Titel: |
 |
|
ach so!
aber: wird man jetzt wirklich schwerer oder leichter?
|
|
 |
koppi89
Anmeldungsdatum: 03.03.2006
Beiträge: 15
|
 koppi89 Verfasst am: 03. März 2006 17:54 Titel: koppi89 Verfasst am: 03. März 2006 17:54 Titel: |
 |
|
ach so!
aber: wird man jetzt wirklich schwerer oder leichter?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. März 2006 17:59 Titel: dermarkus Verfasst am: 03. März 2006 17:59 Titel: |
 |
|
Hm 
Zuletzt bearbeitet von dermarkus am 22. März 2006 15:44, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. März 2006 20:44 Titel: dermarkus Verfasst am: 07. März 2006 20:44 Titel: |
 |
|
Dass du ausdauernd nachgefragt hast, spricht dafür, dass du eine glaubwürdige Quelle dafür hast, dass man auf dem Mount Everest tatsächlich leichter ist. Ich habe die Zeit gefunden, mich da mal ausführlicher damit zu beschäftigen, und muss jetzt sagen, dass ich unrecht hatte:
Du hast recht, auf dem Mount Everest ist man tatsächlich etwas leichter !
Durch die Höhenzunahme wird man da oben um 0,28 % leichter, und durch die Masse des Gebirges wird man um knapp 0,1 % schwerer.
Also wird man auf dem Mount Everest im Vergleich zu einer Position auf Meereshöhe insgesamt um rund 0,2 % leichter.
------------------------------------------------------------------
Ausführliche Begründung:
------------------------------------------------------------------
1.) Die Abnahme von g durch die Höhenzunahme, also die größere Entfernung vom Erdmittelpunkt, nennt man auf Englisch "Free Air Correction". Man berechnet sie mit dem Gravitationsgesetz:
 = \frac{G\cdot M_{\mathrm{Erde}}}{r^2} )
Dabei ist G die Gravitationskonstante
G = 6,67 * 10^-11 Nm^2/kg^2
und M_Erde die Masse der Erde
M_Erde= 6*10^24 kg
Eine Vergrößerung des Abstandes vom Erdmittelpunkt um die rund 9 km, die der Mount Everest hoch ist, bedeutet eine Vergrößerung von r von ungefähr
r_0=6400 km auf r_1 = 6409 km
Damit erhalte ich eine Abnahme von g um 0,28 %.
Das entspricht also einer Abnahme von g um rund 0,03 % pro Kilometer Höhenzunahme durch diesen Effekt.
------------------------------------------------------------------------------
2.) Die Zunahme von g mit zunehmender Höhe auf dem Festland durch die zusätzliche Masse, die sich in dem Berg oder in der Hochebene befindet, nennt man Bouguer-Korrektur.
Um diese zu berechnen, nimmt man eine unendlich ausgedehnte Schicht der Höhe h an, die als zusätzlich Masse eine Gravitationsbeschleunigung bewirkt, und wenn man zum Rechnen die Dichte von Felsgestein als 2,67 g/cm^3 einsetzt, bekommt man damit das Ergebnis, dass die Erdbeschleunigung g durch diesen Effekt um 0,011 % pro Kilometer Höhe zunimmt. Für den Mount Everest bedeutet das in 9 km Höhe eine Zunahme von g um 0,1 % durch diesen Effekt.
(Nachlesen kann man die Grundlagen dazu z.B. auf Englisch unter http://en.wikipedia.org/wiki/Gee)
Wenn ich zum Selberrechnen den Mount Everest als einen Würfel mit Kantenlänge 9 km und der Dichte 2,67 g/cm^3 annehme, dann ist seine Masse M_Berg = 2,67 g/cm^3 * (9 km)^3 = 2 * 10^15 kg, und mit dem Abstand r_Berg= 4500 m zu seinem Schwerpunkt erhalte ich für die von ihm verursachte zusätzliche Gravitationsbeschleunigung g_Berg mit der Formel von oben:
^2} \approx 7\cdot 10^{-3} \frac{m}{s^2} \approx 0,0007 \cdot g )
Also ein Ergebnis, das ungefähr in der richtigen Größenordnung liegt. Zum Vergleich das experimentell von Satelliten gemessene Ergebnis, das man auf Schwerekarten der Erde gemittelt für das gesamte Himalaya ablesen kann, das ist um ca. eine Größenordnung kleiner:
 . .
|
|
 |
Opa
Gast
|
 Opa Verfasst am: 19. März 2006 03:42 Titel: Schwerkraft am Brocken Opa Verfasst am: 19. März 2006 03:42 Titel: Schwerkraft am Brocken |
 |
|
Oh, Ihr seid bei einem grundlegenden Gesetz der Physik. Allerdings ist die Fragestellung nicht vollkommen, daher auch die Antwort nicht, mit Verlaub. Denn die ganze Aufgabe sollte zwei Teile haben und etwa so lauten:
Du stehst am Fuße eines Berges, des Brockens im Harz, und Dein Gewicht sei dort 100 kg.
Ich ersetze den Mount Everest durch den Brocken deshalb, weil es am Brocken einen veröffentlichten Versuch mit Ergebnis gegeben hat.
a) Du steigst auf den Berg, bist Du oben leichter oder schwerer?
b) Du steigst herab und fährst nun in einen neben dem Berg liegenden Bergwerksschacht ein, vielleicht hundert Meter tief; bist Du unten im Schacht schwerer oder leichter?
Begründe Deine Antworten zu a) und b), bitte ohne jede Formel, denn der große Euler (1768) und schon der kaiserliche Mathematiker Ioannes Kepplervs, hundert Jahre vor Newton, kannten die richtigen Antworten.
Wenn aber jemand mit Formeln rechnen will und kann, dann bitte ich um Nachrechnung des am Brocken zustandegekommenen Ergebnisses:
„Ein Wasserwürfel von 1 Meter Kantenlänge wiegt oben auf dem Harz (auf dem „Torfhaus“) etwa 86 Gramm weniger als unten, 500 Meter tiefer, in Harzburg“.
(K. Jung, Schwerkraftverfahren in der angewandten Geophysik, Geophysikalische Monographien, Bd. 2, Leipzig 1961, Seite 52).
Das wäre eine Antwort zum Frageteil a). Bleibt noch b). Und vor allem bleibt die Forderung nach einer einleuchtenden Erklärung.
(Die Rechnungen galten übrigens als so kompliziert, daß man sie auf dem Gymnasium nicht durchführte).
Eigentlich müßte ich noch aus Eulers Brief vom 28. August 1768 zitieren, sowie die Sätze von Kepler. Das sind ganz wundervolle Sätze unserer größten Gelehrten. Man sage, ob man sie hören will. Überhaupt ist die Sache nicht so einfach, wie man an Sätzen des großen Descartes ablesen kann, 1635 an Mersennes: „Ich glaube ... nicht mehr, daß die schweren Körper .. herabkommen ... durch irgendeine Anziehungskraft der Erde.“ Er vertrat die andere Möglichkeit, daß quasi der „Himmel“ draußen die Körper gegen die Erde treibt.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. März 2006 00:04 Titel: Re: Schwerkraft am Brocken dermarkus Verfasst am: 20. März 2006 00:04 Titel: Re: Schwerkraft am Brocken |
 |
|
Hallo Opa!
Das ist ja interessant, Messwerte zu haben, mit denen man die Überlegungen handfest überprüfen kann! Und Ergebnisse früherer Wissenschaftler zu diesem Thema zu hören!
---------------------------------------------------------
Hm, meine Antwort auf a) ist: "man wird leichter", und die Antwort auf b) ist: "Man wird schwerer". Als Begründung ganz ohne jede Formel kann ich nur vermuten: "Man misst es so" (Ohne dass ich bisher eine Messung zu b) kenne). Ich habe die Vermutung, dass man für eine Erklärung mindestens eine Abschätzung der Dichte des Berges bzw. des Bodens sowie der Erde braucht.
Die Begründung von Euler und Kepler würde mich daher sehr interessieren!
Meine Antwort mit Formeln führt über die Ergebnisse für die Free Air Correction (FAC) und die Bouguer-Korrektur, die ich oben schon mal angegeben hatte:
a) am Berg addieren sich die beiden Effekte wie folgt:
 \frac{h}{\mathrm{km}} g_0 = (-0,0002) \frac{h}{\mathrm{km}} g_0 = -0,0002 \cdot 0,5 \cdot g_0 = -0,0001 \cdot g_0 )
Also um 0,01 % leichter.
Das liegt allerdings noch gut einen Faktor 2 über dem Messresultat von oben (-0,038 kg / 1000 kg = -3,8*10^{-5}).
Also fehlt da noch was: Ich habe noch nicht berücksichtigt, dass am Fuße des Berges die Masse des Berges in unmittelbarer Nähe ist und daher nach oben zieht. Dieser Effekt bringt maximal noch einmal den Bouguer-Beitrag für die Differenz der Werte unten und oben, und damit:
 \frac{h}{\mathrm{km}} g_0 = (-0,00009) \frac{h}{\mathrm{km}} g_0 = -0,00009 \cdot 0,5 \cdot g_0 = -0,000045 \cdot g_0 )
Also schon fast der zu erklärende Wert. Die nun noch bleibende kleine Differenz erkläre ich mir damit, dass die mittlere Dichte des Brockens ein bisschen größer sein wird als die 2,67 g/cm^3, mit denen ich die Bouguer-Korrektur berechnet habe.
b) unterirdisch leite ich mir das folgendermaßen her:
1. Man entferne die Schicht von 100 m Dicke unter dem Probekörper. Dann zieht diese nicht mehr von unten am Probekörper, der wird dadurch leichter
2. Dann bewege man den Körper die 100 m nach unten. Dadurch wird er schwerer
3. Dann füge man wieder die Schicht von 100 m Dicke hinzu. Sie zieht nun zusätzlich von oben. Dadurch wird er leichter.
Also addiere ich einmal die FAC positiv hinzu und subtrahiere zweimal die Bouguer-Korrektur.
Also
 \frac{h}{\mathrm{km}} g_0 = (+0,00009) \frac{h}{\mathrm{km}} g_0 = 0,00009 \cdot 0,1 \cdot g_0 = + 9 \cdot 10^{-6} \cdot g_0 )
Also ist nach meiner Rechnung der Probekörper in 100 m Tiefe um 0,0009 % schwerer.
-------------------------------------------------------------------------
Die Herleitung der Formeln mache ich wie folgt:
Free Air Correction:
Die Gravitationsbeschleunigung in der Höhe h über einer kugelrunden Erde mit Radius R_E, durchschnittlicher Dichte \rho_E und Masse M_E ist:
= G\frac{M_E}{(R_E+h)^2}=G\frac{\varrho_E\cdot (4/3)\pi R_E^3}{(R_E+h)^2}=\frac{4\pi}{3}\varrho_E G R_E \left(1+\frac{h}{R_E} \right)^{-2} \approx \frac{4\pi}{3}\varrho_E G R_E \left(1-2\frac{h}{R_E} \right))
Beim Entwickeln habe ich verwendet, dass h/R_E << 1 ist.
Dabei ist die Dichte der Erde
R_E^3} = \frac{5,97\cdot 10^{24}\,kg}{(4 \pi / 3) (6370 km)^3} = 5,51\, g/cm^3 )
Damit ist die Änderung von g durch die Free Air Correction, bezogen auf den Wert beim Radius R_E, gleich:

g_0 sei der Wert von g am Fuß des Berges, für die Umformung oben habe ich rund 10 m/s^2 verwendet.
Bouguer-Korrektur:
Die Gravitationsbeschleunigung durch eine kreisförmige Scheibe der Höhe h, der Dichte \rho_S und dem Radius 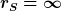 auf einen Körper, der sich direkt auf (oder unter) der Scheibe befindet, ist (in Zylinderkoordinaten r, H, und \phi angesetzt): auf einen Körper, der sich direkt auf (oder unter) der Scheibe befindet, ist (in Zylinderkoordinaten r, H, und \phi angesetzt):
 = \int_{V} G\frac{\varrho_S dV}{r^2+H^2} \cos\left(\arctan\left(\frac{r}{H}\right)\right)= \varrho_S G \int_{\varphi=0}^{2 \pi} \int_{H=0}^{h} \int_{r=0}^{\infty} \frac{r}{r^2+H^2}\cos\left(\arctan \left(\frac{r}{H}\right) \right) d\varphi dr dH)
 \right) dr dH =2 \pi \varrho_S G \int_{H=0}^{h} \left[-\frac{1}{\sqrt{(r^2/H^2)+1}}\right ]_{r=0}^{r=\infty} dH)

Für \rho_S = 2,67 g/cm^3 (Dichte von Felsgestein) ist also:
 = 2\pi \varrho_S G h = 1,12\cdot 10^{-6} \frac{1}{\mathrm{s}^2} \cdot h \approx +1,1\cdot 10^{-4} \frac{h}{\mathrm{km}} \cdot g_0 )
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 20. März 2006 09:25 Titel: Euler, Kepplervs, Wagenschein Opa Verfasst am: 20. März 2006 09:25 Titel: Euler, Kepplervs, Wagenschein |
 |
|
Lieber dermarkus,
Opa hat sich außerordentlich gefreut über das große Interesse an Euler und Kepler und an der Sache selbst. Die wundervollen Sätze der beiden werde ich gleich abschreiben aus meiner Quelle, da sie ansonsten nur schwer zu finden sind.
Ich staune über die ausführlichen Formelrechnungen, doch das Ergebnis gefällt mir nicht:
„Also ist nach meiner Rechnung der Probekörper in 100 m Tiefe um 0,0009 % schwerer.“
Denn daraus würde vielleicht folgen, daß man um so schwerer wird, je tiefer man in die Erde hineinfährt. Viele sind aber der Meinung, man würde im Mittelpunkt der Erde gar nichts wiegen. Ich glaube das auch. Einen Satz Eulers will ich vorweg schreiben:
„Dem unerachtet findet man noch in dieser Sache viele Schwierigkeiten, die es der Mühe werth ist zu heben ...“
1) EULER an die kleine Prinzessin Friederike von Brandenburg, am 28. August 1768:
„Nachdem man ... anfieng, einzusehen, daß die Figur der Erde ungefähr kugelförmig und allenthalben bewohnbar sey, so das es Oerter gebe, die uns gerade entgegen gesetzt sind, wo die Einwohner uns die Füße zukehrten, die man auch deswegen Antipoden nennt: so fand diese Meynung so viel Widersprüche, daß einige Kirchenväter sie als eine große Ketzerey ansahen ... Heut zu Tage würde man für einen Thoren gehalten werden, wenn man an ihrer Wirklichkeit zweifeln wollte ... Dem unerachtet findet man noch in dieser Sache viele Schwierigkeiten, die es der Mühe werth ist zu heben .... In der Verlegenheit ... haben einige sie durch die Vergleichung mit einer Kugel zu heben geglaubt, auf deren Oberfläche man oft Fliegen ... eben so wohl oben als unten herumlaufen sieht ... Aber sie denken nicht daran, daß die Insekten ... sich durch ihre Klauen anhaken ... Also müßte der Antipode wohl vielleicht Haken an seinen Schuhen haben ... ; aber er hat keine ... Ja, so wie wir uns einbilden oben auf der Erde zu seyn, so bildet es sich der Antipode auch ein und glaubt, daß wir unten sind. Vielleicht ist es ihm eben so bange um uns als uns für ihn ist ... In der That, wenn sich jemand an der Decke eines Zimmers mit den Füßen halten wollte, so müßten die Haken an seinen Schuhen sehr stark seyn, und bey alledem würde er doch eine traurige Figur vorstellen ... Aber wohin sollte denn nun wohl der arme Antipode, für den man so besorgt ist, fallen, wenn sich das ereignete? ... niemals hat man noch gehört, daß ein Antipode einen so schrecklichen Fall von der Erde hinweg gethan hätte. Vielmehr, wenn sie fallen, so fallen sie wie wir gegen die Erde zu; und doch bilden sie sich ein, nach unten zu fallen. - Allenthalben wo wir uns auf der Erde befinden, ist unten da, wohin die Körper fallen.“
... „Die Philosophen streiten sehr darüber, ob es wirklich eine solche Kraft gebe, die unsichtbar auf alle Körper wirkt und sie nach unten treibt; oder ob es vielmehr eine innere, in dem Wesen der Körper liegende Eigenschaft, und gleichsam eine Art von Instinkt sey, die sie treibt, sich gegen die Erde zu bewegen. Diese Frage läßt sich auf eine andere bringen: ob die Ursache der Schwere in der Natur jedes Körpers selbst, oder ob sie außer ihm existirt ...“
Bei der einfachen Frage nach der Ursache, da gibt es in der Tat mindestens zwei grundlegend verschiedene Möglichkeiten beim geworfenen und fallenden Stein: a) Der Himmel könnte ihn nach unten drücken; b) Die Erde könnte ihn nach unten ziehen. Cartesius bevorzugte die Lösung a).
2) DESCARTES, 1635 an Mersennes: „Ich glaube ... nicht mehr, daß die schweren Körper ...
herabkommen ... durch irgendeine Anziehungskraft der Erde“; 1639 an De Beaune: „Bezüglich der Schwerkraft stelle ich mir nichts anderes vor, als daß die gesamte feine Materie, die sich von hier bis zum Mond erstreckt, durch sehr schnelle Drehung um die Erde alle Körper, die sich nicht so schnell bewegen können, gegen diese treibt.“ - Er sucht also die Ursache nicht in der Erde, sondern draußen!
3) Ein Versuch, veröffentlicht 1961: Ein Wasserwürfel von 1 Meter Kantenlänge wiegt oben auf dem Harz (auf dem „Torfhaus“) etwa 86 Gramm weniger als unten, 500 Meter tiefer, in Harzburg. - Das spricht für eine sich in die Ferne allmählich verlierende Zugkraft der Erde. - Es paßt recht gut zu der Vorstellung, sie könnte im Erdmittelpunkt hausen, von ihm ausgehen. Wäre dies aber nun tatsächlich der Fall, dann müßte unten im Bergwerksschacht unter der Erde aber zu erwarten sein, daß das Gewicht der Dinge, die da hinuntergebracht werden, zunähme, denn sie kommen ja dem Mittelpunkt näher.
4) EULER: „Wir sehen also nun ein, ... daß diese Kraft auf der Oberfläche der Erde am stärksten wirkt; daß sie sich vermindert, wenn man sich von dieser Oberfläche entfernt, es mag dies nun geschehen, indem man in die Erde hinein gegen den Mittelpunkt zugeht, oder indem man von ihr weg in die Höhe steigt.“ Dazu kommt, was Euler so sagt:
„Ich habe schon Ew. Hoheit gezeigt, daß man in der That beobachtet haben will, daß ein großer Berg in Amerika eine kleine ATTRAKTION hervorgebracht hätte.“
Damit kommen wir der Lösung wesentlich näher: gemeint ist die Lotabweichung eines Pendels in der Nähe eines Gebirges. Sie ist außerordentlich gering, aber doch da. In Harzburg beträgt sie nur 1/240 Grad. - Besser und einleuchtender: Durch die „Attraktion“ steigen die Oberflächen der beiden Teiche bei Harzburg nach Süden hin an um 1 cm auf 153 Meter Länge. Die Wassertröpflein der Teiche „spüren“ das Gebirge.
Sie stauen sich ein wenig auf den Harz hin. Und alle Bäume rings um den Harz herum spüren seine Kraft und machen eine kleine Verbeugung zum dicken Brocken hin.
5) KEPPLERVS, der kaiserliche Mathematiker: a) „ ... ob der stain nach dem Mittelen der Welt zile oder nach dem Mittelen der Erdkugel. Jch sage, nit nach dem Mittelen der Welt, sondern nur nach dem Mittelen der Erdkugel. Dan da sihet man die Vrsache, die Erd zeucht solliche schwäre dinge an sich wie ein Magnet das Eisen.“ .....
b) „das alle sachen nach dem saiger ... vnder sich fallen ... das macht die anziehende gewalt der Erden, die steckht nit im Centro sondern im gantzen leib, und ziehen diejenige stuckh am maisten,
die dem auffgeworffenen stain am nechsten seind.“ c) die fallenden Steine „begehren nit des orts, wie Aristoteles will, sondern nur des leibes.“
Es gibt also im Erdmittelpunkt kein einziges Männlein, das uns an Gummischnüren zieht. Nit im Centro.
Sondern alle Teile des Leibes eines Körpers bringen ATTRAKTIONEN hervor, die sogenannten Massenanziehungskräfte.
Zur Verdeutlichung, zum exakten Verstehen, da muß man sich drei einfache Zeichnungen machen.
1. Ein Strichmännlein auf einem langen, ganz leicht gebogenen Strich, der Erdoberfläche.
Man male nun kleine u-förmige Schollen, wie etwa Fischschuppen, unter den Strich, mehrere Reihen davon untereinander, vielleicht fünf bis sieben, das sollen Keplers Stücklein von kleinen Massen sein, Erdschollen gewissermaßen.
Man zeichne anschließend noch ungefähr einen Halbkreis unter dem Männlein. Der Halbkreis enthält dann eine gewisse Menge von Schollen, und das sind Kepplers „stuckh“, die „am maisten“ ziehen, die dem Männlein „am nechsten seind“.
Diese erste Zeichnung soll ungefähr in der Mitte eines Blattes Papier angelegt werden, im mittleren Drittel des Blattes.
2. Man zeichne jetzt neben dem Männlein, ins obere Drittel des Blattes hinein, einen Berg, unten breit, oben spitz zulaufend. Die Bergspitze sollte dabei, das ergibt sich meist von selbst, wesentlich schmaler sein als der Halbkreis von Zeichnung 1. Nun kopiere man das Männlein samt seinem Halbkreis voller Massenschollen derart auf den Berg, daß es mit seinen Füßen genau auf der Bergspitze steht!
Das ergibt die erste Lösung: Der Halbkreis mit seinen Stücklein darin ist auch noch rechts und links von der Bergspitze, diese Stücke von Schollen hängen sozusagen in der Luft. Räumlich gedacht wäre der Halbkreis eine Halbkugel mit noch mehr Massenstücklein darin, die um die Bergspitze herum da in der Luft hängen. In der Luft hängen heißt dann aber: Sie sind eigentlich nicht mehr vorhanden!! Oben auf der Bergspitze ziehen also weniger Massenstücklein an dem Srichmännlein.
Deshalb wird man oben leichter.
3. Im unteren Drittel des Blattes zeichne man zuletzt den schmalen Bergwerksschacht und stelle das Männlein unten auf den Grund des Schachtes. Anschließend zeichne man diesmal den Halbkkreis
über dem Kopf des Männleins!! In dem Halbkreis befinden sich nun bereits diejenigen Stücklein von Massen, die das Männlein über dem Kopfe hat. Und diese ziehen das Männlein nach oben!
Deshalb werden Bergleute unter Tage eine Spur leichter, als sie es oben waren.
Zitiert aus Martin Wagenschein, Ursprüngliches Verstehen und exaktes Denken, Band II, Klett, 1970, S. 25 bis 40. Da steht noch einiges mehr.
Zuletzt bearbeitet von Opa am 21. März 2006 00:01, insgesamt einmal bearbeitet |
|
 |
Gast
|
 Gast Verfasst am: 20. März 2006 12:20 Titel: Gast Verfasst am: 20. März 2006 12:20 Titel: |
 |
|
> Deshalb werden Bergleute unter Tage eine Spur leichter, als sie es oben waren.
Das wäre so, wenn die Erde eine konstante Dichte hätte. In diesem Fall könnte man
die Gewichtskraft einfach durch F(r) = m*g*r/R ausdrücken, mit R = Erdradius, und
die Beschleunigung ergibt sich dann als a(r) = g*r/R, im Zentrum also null.
Auch wenn es "im Centro" wohl kein Männlein gibt, das an uns zieht, der Zusammenhang
kann schon mit einem solchen Feder-Modell beschrieben werden. Es zieht um so stärker,
je weiter wir von ihm entfernt sind. Über der Erdoberfläche gelten dann neue Regeln.
Jetzt ist die Dichte des Erdmantels aber größer als die der Erdkruste. Dadurch nimmt
die Beschleunigung bei der Reise zur Erdmitte erst etwas zu und dann stetig ab.
Es ist also zu erwarten, dass das Gewicht dem gleichen Verlauf folgt.
Wir wohnen auf der Schale des Erd-Apfels...
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 20. März 2006 23:51 Titel: Gast schrieb Opa Verfasst am: 20. März 2006 23:51 Titel: Gast schrieb |
 |
|
„... der Zusammenhang kann schon mit einem solchen Feder-Modell beschrieben werden. Es zieht um so stärker, je weiter wir von ihm entfernt sind. Über der Erdoberfläche gelten dann neue Regeln.“
Aber, aber, ein Federmodell? Ist damit eine Federwaage gemeint, die man im Physikunterricht oben an einem Stativ befestigt, dann unten an ihre Feder Stücke anhängt, deren Gewicht man dann ablesen kann an einer aus dem Gehäuse herauskommenden Skala? Falls ja, dann gebe ich zu bedenken: die Lotabweichung eines Pendels neben einem Gebirge, - Eulers Berg in Amerika brachte Attraktionen hervor. Die Federwaage müßte in diesem Falle waagerecht angebracht werden? Wie denn?
Sie taugt anscheinend wenig als Modell hier.
Und unterirdisch waagerecht? Zum Beispiel zwischen einem besonders dichten Felsbrocken mit Silber oder Gold darin und einer waagerecht davon liegenden einfachen Erdscholle?
Oder zwischen zwei Massenstücken beliebiger Dichte, von denen eines links oben und das andere rechts unten liegt, egal ob beide oberirdisch oder unterirdisch liegen.
Außerdem widersprechen des Gastes Ausführungen ein wenig sich selbst, vor allem aber dem Euler und dem Kepler und dem Wagenschein, ferner dem Newton und dem Einstein sowie schließlich auch dem Opa.
Es macht wenig Sinn, Federwaagen, Beschleunigung oder Formeln, die auf null kommen, oder Dichten einzuführen, wenn nicht geklärt ist, worum es überhaupt geht.
Wenn unser Männlein im Mittelpunkt der Erde nichts wiegt, dann bedeutet das nicht, daß keine Massenanziehungskräfte, keine Schwerkraft, keine sogenannte Erdanziehung mehr vorhanden sind. Im Gegenteil, dort wirken sie wohl am stärksten und rundum, zwischen der Männleinmasse und den überall rundum liegenden Stücklein Erden. Nur, im gedachten Idealfall, da wird dort das Männlein von überall rundumher von gleichen Massen angezogen, so daß alle Massenanziehungskräfte sich gegenseitig „aufheben“.
Vielleicht taugt das Modell Federwaage doch etwas im Erdmittelpunkt, wenn man rundum am Männlein tausende Federwaagen anhängen können würde und jeweils das andere Ende der Federwaagen mit den rundumliegenden Massenstücklein verbinden könnte.
Jede einzelne Federwaage würde dann sicherlich etwas anzeigen oder nicht?
Deshalb werden Bergleute unter Tage eine Spur leichter, als sie es oben waren.
Das hat Wagenschein geschrieben, in Übereinstimmung mit Euler und Kepler. - Gast bezweifelt es? Er könnte sich die drei beschriebenen Zeichnungen anfertigen, die vielleicht dann zur Verständigung beitragen mögen.
Über Tage haben die Bergleute Luft über ihren Köpfen; unter Tage haben sie „Erden“, wie Kepler sagt, über ihren Köpfen, egal welcher Dichte, jedenfalls „dichter“ oder schwerer als Luft. Diese Massen über den Köpfen der Bergleute ziehen wie Magnete per Massenanziehungskraft,
per „Gravitation“, die Bergleute unter Tage nach oben. Die Bergleute werden deshalb eine Spur leichter.
Nicht aber werden sie unter Tage erst schwerer und dann leichter, nein sie werden sofort leichter, schon bei einem einzigen Millimeter unter Tage.
Und wenn der Bergmann über Tage da noch auf einen Kasten (Bier) steigt, dann wird er ebenfalls um eine geringe Spur leichter. (Vgl. Euler). Ist schon erstaunlich.
Oder Faust I, Studierzimmer, (Mephistopheles):
Da seht, daß Ihr tiefsinnig faßt,
Was in des Menschen Hirn nicht paßt!
|
|
 |
Gast
|
 Gast Verfasst am: 21. März 2006 03:52 Titel: Gast Verfasst am: 21. März 2006 03:52 Titel: |
 |
|
> Ist damit eine Federwaage gemeint
Nicht die Waage selbst, nur ihr Funktionsprinzip im übertragenen Sinne. Der gleiche Formalismus, der den Zusammenhang von Kraft und Weg bei einer Feder beschreibt, ist auch auf die Schwerkraft innerhalb der Erde anwendbar, aber auch nur innerhalb. Oben ist der Kopf in der Tat leichter als die Füße, selbst ohne Bierkiste, wenn auch nur sehr, sehr wenig. Meine Darstellung des Verlaufs der Gravitation innerhalb der Erde stammt übrigens ursprünglich von einem Zeitgenossen Newtons, von Robert Hooke, und ist in vollem Einklang mit Newtons Theorie der Gravitation, an deren Formulierung Hooke erheblichen Anteil hatte, was Newton aber gern unerwähnt ließ.
Nur wussten die beiden damals nichts über den inneren Aufbau der Erde, sonst hätten sie mir sicher zugestimmt, denn es folgt aus genau den Theorien, die sie entwickelt haben und die sich bis heute als brauchbar erwiesen haben um solche Zusammenhänge zu beschreiben.
Die mittlere Dichte der Erde ist etwa 5,5 g/cm^3, die der Gesteine nahe der Oberfläche im Durchschnitt aber nur 2,7 g/cm^3, und das viele Wasser hat gar nur etwas mehr als 1 g/cm^3. Manchmal hilft es dem Verständnis, wenn man die Verhältnisse stark übertreibt um damit den wesentlichen Zusammenhang zu verdeutlichen. Nehmen wir dazu an, die Erdkruste wäre aus Schaumstoff, vielleicht doppelt so dicht wie Luft.
 http://upload.wikimedia.org/wikipedia/de/thumb/e/e5/Aufbau_der_erde_schematisch.png/300px-Aufbau_der_erde_schematisch.png http://upload.wikimedia.org/wikipedia/de/thumb/e/e5/Aufbau_der_erde_schematisch.png/300px-Aufbau_der_erde_schematisch.png
40 km Schaumstoffkruste also, dann fängt der solide, dichte Teil an, der Erdmantel. Würden wir dann nicht, um im Bild zu bleiben, auf der Bierkiste stehen? Und wenn wir einen Schacht graben würden nach unten in den Schaumstoff, wäre das nicht so, als würden wir gewissermaßen von der Kiste hinunter steigen?
Wenn man wissen will, ob dieses Bild auch der Realität entspricht, dann muss man es mit bekannten Daten durchrechnen. Das ist getan worden und das Ergebnis war der beschriebene Verlauf der Schwerkraft. Das heißt nicht, dass es stimmt, es heißt nur, dass ich keine Informationen habe, die dem widersprächen.
> Jede einzelne Federwaage würde dann sicherlich etwas anzeigen oder nicht?
Nein, nichts. Der Innenraum einer 'massiven' Hohlkugel ist frei von Schwerkraft, egal wo man sich dort aufhält, einschließlich der inneren Oberfläche, so Newton. Aber die Uhren gehen dort langsamer als bei uns hier oben, und die auf einem hohen Berg gehen schneller als unsere hier unten, so Einstein. Ist schon erstaunlich.
Die Sonne dreht sich um die Erde, das sieht man doch nun jeden Tag. Kein vernünftiger Mensch kann daran zweifeln. In 'des Menschen Hirn' hat auch erst mal nicht gepasst, dass schwere Gegenstände nicht schneller fallen als leichte, und doch ist es so. Das Lernen hört niemals auf.
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 21. März 2006 12:47 Titel: Opa Verfasst am: 21. März 2006 12:47 Titel: |
 |
|
> Das Lernen hört niemals auf. <
O edler Gast, wie wahr und wie unwahr.
Das bunte Bild ist ganz wundervoll, wenn es auch mit dem Thema Gravitation nur wenig zu tun haben dürfte, auf den ersten Blick. (Wie kann man so ein Bild einfügen?) Ich habe es kopieren können in eine Worddatei hinein, und siehe da, es erschien die Aufforderung, zu klicken. Da bin ich dann bei einer Wikipediaseite gelandet. Da wiederum gibt es einen Klick zum Thema Gravitation. Dort steht
„Das newtonsche Gravitationsgesetz besagt, dass sich die Gravitationskraft F, mit der sich zwei Massen m1 und m2 anziehen, proportional zu den Massen beider Körper und umgekehrt proportional zum Quadrat des Abstandes r der Massenschwerpunkte verhält: ......
Aus dem newtonschen Gravitationsgesetz folgt, dass die Gravitation an einem Punkt einer sphärisch symmetrischen (kugelförmigen) Massenverteilung im Abstand r von ihrem Schwerpunkt stets so groß wie die Gravitation einer Punktmasse in diesem Schwerpunkt ist, deren Masse gerade dem Teil der Gesamtmasse entspricht, der sich innerhalb der Kugel mit dem Radius r befindet. Innerhalb einer homogenen Kugel bedeutet das, dass die Gravitationskraft proportional zum Abstand vom Mittelpunkt ist. Die Gravitation einer homogenen Kugel im Vakuum ist daher an ihrer Oberfläche am größten. Das gilt auch für die Erde.“
Die letzten beiden Sätze entsprechen ungefähr dem, was Euler sagt:
4) EULER: „Wir sehen also nun ein, ... daß diese Kraft auf der Oberfläche der Erde am stärksten wirkt; daß sie sich vermindert, wenn man sich von dieser Oberfläche entfernt, es mag dies nun geschehen, indem man in die Erde hinein gegen den Mittelpunkt zugeht, oder indem man von ihr weg in die Höhe steigt.“
Daher nehme ich an, daß die zitierten Ausführungen in Wikipedia wohl richtig sein dürften. Oder andersherum, Kepplervs, der kaiserliche Mathematiker und Astronom, der beschrieb die Sache richtig, ebenso stimmen Eulers Sätze. Und ferner lehrte Newton im Grunde das, was Kepler bereits mit dem Herzen verstanden hatte. Und Euler (1707 -1787), der lehrte ziemlich genau das, was Newton (1643 - 1727) hundert Jahre zuvor gelehrt hatte. Und Wikipedia lehrt 2006 nichts anderes als Kepler (1571-1630). Mit anderen Worten, das Wissen der Menschheit über das eigentliche Wesen der Gravitation besteht seit 400 Jahren. Opa würde ja gerne, lernbegierig, wie er ist, wesentlich Neues dazulernen in Sachen Grundverständnis der Gravitation oder Massenanziehungskraft. Doch er fand nicht Neues, selbst nicht bei Wikipedia.
Gast hat allerdings wunderlich Neues.
> Jede einzelne Federwaage würde dann sicherlich etwas anzeigen oder nicht?
Nein, nichts. Der Innenraum einer 'massiven' Hohlkugel ist frei von Schwerkraft, egal wo man sich dort aufhält, einschließlich der inneren Oberfläche, so Newton.<
Nein, das kann Newton nicht gelehrt haben. Im Gegenteil, er lehrte, daß die Gravitation überall in unserem Sonnensystem vorhanden ist. Folglich gibt es sie auch innerhalb einer 'massiven' Hohlkugel, - was ist damit denn bitte gemeint?
Manchmal liest und hört man ja, die Astronauten auf der Reise zum Mond seien in den Bereich der Schwerelosigkeit eingetreten. Nach Newton aber gibt es da zwischen Mond und Erde keinen solchen Bereich, denn nach wie vor wirken die Gravitationskräfte vom Mond und die von der Erde auf die Astronauten ein. Das wäre eine Sache für zwei „Federwaagen“. Eine davon zwischen Astronaut und Erde, die andere zwischen Astronaut und Mond. Ob die beiden „Federwaagen“ da an dem Pünktlein, an dem sich die Gravitationen von Mond und Erde gegenseitig „aufheben“, etwas anzeigen würden? Wenn’s ordentliche Gravitationsfederwaagen sind, dann könnten sie was anzeigen oder nicht?
Da steh ich nun, ich armer Thor!
Und bin so klug als wie zuvor.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. März 2006 13:33 Titel: dermarkus Verfasst am: 21. März 2006 13:33 Titel: |
 |
|
Das ist ja eine Goldgrube!
Den schönen Zitaten spüre ich den Geist der Wissenschaft an, der neuen Gesetzmäßigkeiten auf der Spur ist, indem er die Natur in Modellen betrachtet, die so klar und vereinfacht sind, dass die Gesetzmäßigkeiten klar hervortreten. Das war zu Zeiten von Galilei, Kepler und Newton nicht selbstverständlich, sondern eine der großen Errungenschaften der damaligen Wissenschaft.
| Opa hat Folgendes geschrieben: |
... gemeint ist die Lotabweichung eines Pendels in der Nähe eines Gebirges. Sie ist außerordentlich gering, aber doch da. In Harzburg beträgt sie nur 1/240 Grad. - Besser und einleuchtender: Durch die „Attraktion“ steigen die Oberflächen der beiden Teiche bei Harzburg nach Süden hin an um 1 cm auf 153 Meter Länge. Die Wassertröpflein der Teiche „spüren“ das Gebirge.
Sie stauen sich ein wenig auf den Harz hin.
|
Dann weiß ich jetzt auch, woher die Messdaten der Aufgabe stammen können, die ich neulich hier (http://www.physikerboard.de/htopic,4730,bergsee.html) im Forum gesehen habe!
Und aus dem schönen Euler-Zitat sowie Gasts Ausführungen entnehme ich, dass sich Eulers, Opas, Gasts und meine Erkenntnisse vereinen lassen:
Euler spricht nicht von einer Abhängigkeit der Dichte der Erde vom Radius in ihrem Inneren. Er spricht also von einer Kugel mit homogener Masse. Für eine solche Massenverteilung muss also die Veränderung von g nahe unter der Erdoberfläche dieselbe Richtung haben wie tief unter der Oberfläche. Und weil in der Tat in der Mitte die Gravitationsbeschleunigung Null ist (von allen Seiten ziehen dort die Massen gleich stark), nimmt die Gravitationsbeschleunigung mit zunehmender Tiefe ab, wie Opa sagt, und Euler auch. Damit bin ich einverstanden. In Gasts Federmodell heißt das also, die Gravitationskraft der Erde wächst innerhalb der homogenen Erde mit zunehmendem Abstand vom Mittelpunkt, und das ist so ähnlich wie bei einer Feder, bei der die Kraft auch mit zunehmender Auslenkung zunimmt. Auch damit bin ich einverstanden.
In meinen Formelrechnungen oben habe ich verwendet, dass die Dichte des Gesteins an der Erdoberfläche kleiner ist als die mittlere Dichte der Erde. (Denn man weiß, in der Mitte der Erde ist Eisen, und das hat eine viel größere Dichte als Stein). Daher verwende ich ein anderes Modell als Euler, und damit komme ich zu dem Ergebnis, dass in der Nähe der Erdoberfläche die Erdbeschleunigung mit zunehmender Tiefe zunächst zunimmt. (Für tiefere Schichten, bei anderen Dichten, ändert sich das wieder, wie Gast richtig sagt.) Diesen Gedanken bringt Gast sehr schön mit seinem anschaulich auf die Spitze getriebenen Beispiel von der Schaumstoffschicht auf den Punkt.
Die Bildlein, die Opa in Worten malt, haben mich inspiriert, malerisch tätig zu werden. (Man verzeihe mir, dass ich am Computer mit meinen bescheidenen Skizzierkünsten das Männlein durch einen roten Punkt ersetzt habe)
Und dabei merke ich, dass man hier tatsächlich in diesen beiden Vergleichsfällen leichter wird: Von 1A nach 1B fällt Masse weg, die nach unten zieht, bei diesem Schritt wird man in der Tat leichter. Von 2A nach 2B kommt oben Masse hinzu, die oben zieht, also wird man auch bei diesem Schritt leichter. (Um zu zeigen, wo die Erdoberfläche ist, habe ich in Bild zwei wieder den schmalen Berg eingezeichnet. Sollte das als verwirrend empfunden werden, dann stelle man sich diesen Berg in Bild 2 als verzierenden Baum vor.  ) )
Aber wenn ich genau hingucke, fehlen in diesen Bildern einige Schritte, die man zum vollständigen Vergleich der Situationen braucht, die wir uns vorgenommen hatten zu vergleichen. Und diese Schritte habe ich dann auch mal mit aufgemalt:
Fall 3 ist der am Berg:
Am Fuß des Berges ist die Ausgangssituation die in 3A. Denkt man sich den Berg weg, dann wird man leichter (3A nach 3B). Bewegt man sich nach oben (in der freien Luft), dann wird man leichter (3B nach 3C). Denkt man sich nun den Berg wieder dazu, dann wird man bei diesem Schritt schwerer (3C nach 3D).
Um den Gesamteffekt herauszufinden, muss man hier also herausfinden, ob die Schritte, bei denen man schwerer wird, oder die Schritte, bei denen man leichter wird, überwiegen. Und dazu braucht man eine Abschätzung für die Dichte des Berges und die mittlere Dichte der Erde.
Fall 4 ist der im Bergwerksstollen:
Ausgangspunkt ist das Männlein auf der Erdoberfläche. Dann denke man sich die Gesteinsschicht (der Dicke von z.B. 100 m ) weg, bei diesem Schritt wird man leichter (4A nach 4B). Dann bewege man sich die 100 m weit nach unten, dabei wird man schwerer. (4B nach 4C). Und dann denke man sich die 100 m Erdschicht wieder dazu (4C nach 4D).
Ob man bei diesem letzten Schritt von 4C nach 4D leichter wird oder nicht, habe ich im Bild offengelassen. Denn findet das ganze in einem Bergwerk auf einer Hochebene statt, dann bin ich einverstanden, dass man bei diesem Schritt leichter wird (so hatte ich oben in meinem vorigen Beitrag auch gerechnet). Findet das ganze aber im Flachland statt, dann muss man das berücksichtigen, was Gast als Newton-Zitat angegeben hat: Innerhalb einer massebehafteten Kugelschale hebt sich die Anziehung dieser Schalenmasse zu Null auf. (das habe ich vorsichtig versucht mit den vielen Pfeilen in Bild 4D anzudeuten). Und weil man sich nun innerhalb dieser Kugelschale befindet, die man nun dazufügt, verändert sich das Gewicht bei diesem letzten Schritt im Flachland nicht.
Ich hoffe, meine Bildlein sind schön genug geworden, um diese Worte unterstützen zu können 
// edit : Das Stirnrunzeln hat mich dazu bewogen, die Bilder noch etwas übersichtlicher zu gestalten. Die roten Pfeile zeigen die Gewichtskraft durch die Masse des Berges oder der Erdschicht, die im nächsten Schritt entfernt wird oder im vorigen Schritt dazugekommen ist.
Erfolgt der Schritt von 4C nach 4D in einem Berg, dann kommt die Schicht obendrauf und zieht nach oben, und man wird bei diesem Schritt leichter. Erfolgt der Schritt von 4C nach 4D aber innerhalb der Erde, (also zum Beispiel ein Bohrloch, das in Tiefen unter Meereshöhe vordringt), dann ist die Schicht, die von 4C nach 4D dazukommt, eine Kugelschale um die ganze Erde herum. Und weil man sich nun innerhalb dieser Kugelschale befindet, bewirkt dies keine Änderung des Gravitationspotentials und keine zusätzliche Gravitationskraft.
| Beschreibung: |
|

Download |
| Dateiname: |
schwererleichter1.gif |
| Dateigröße: |
11.09 KB |
| Heruntergeladen: |
8764 mal |
Zuletzt bearbeitet von dermarkus am 22. März 2006 11:42, insgesamt einmal bearbeitet |
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 21. März 2006 21:04 Titel: Opa Verfasst am: 21. März 2006 21:04 Titel: |
 |
|
Lieber dermarkus,
Euler und Newton und Kepler haben sich sehr gefreut. Endlich mal ein Lob und ein großes dazu.
Können Gast oder dermarkus mir einen Rat geben, eine genaue und ausführliche Hilfesstellung oder Beschreibung, wie auch ich als Opa hier eine Zeichnung hineinstellen kann?
Kepplervs hat sich besonders gefreut über die Zeichnungen 1 und 2. Bei 3 allerdings wurde er unruhig und bei 4 schien er mir gar etwas säuerlich dreinblicken zu wollen. Sir Isaac Newton, der jeden Satz Keplers belauschte, der sogar sein Minenspiel wie kein anderer kennt, wollte sich mit den letzten beiden Zeichnungen dann auch nicht mehr so richtig anfreunden. Euler meinte, ach, was habe ich damals doch für schöne Sätze der kleinen Prinzessin geschrieben. Dann beauftragte er mich, bei den löblichen Herren Gast und dermarkus um Hilfe anzufragen, das Einfügen einer Zeichnung betreffend. Wagenschein meinte, ja dann könntest Du ja auch meine zwei kleinen Zeichnungen mit ins Netz stellen, wenn Du sie gescannt und in jpegs umgewandelt hast.
Zuletzt bearbeitet von Opa am 22. März 2006 02:18, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. März 2006 21:10 Titel: dermarkus Verfasst am: 21. März 2006 21:10 Titel: |
 |
|
| Opa hat Folgendes geschrieben: | ... Das gilt auch für die Erde.“
... Und Wikipedia lehrt 2006 ... |
Ich würde sagen, da hat Opa mit scharfem Auge eine Ungenauigkeit in der Wikipedia entdeckt.
Nach ein bisschen Wühlen und Suchen mit google im Internet habe ich folgendes ausgegraben:
Die Studenten der Geophysik an der TU Braunschweig lernen mit folgendem Skript (Vorwarnung: Diese pdf-Datei ist ein schwerer Brocken von 12,2 MB)
ftp://ftp.geophys.nat.tu-bs.de/pub/publication/script/gp1.pdf
Auf Seite 72 und 73 dieser pdf-Datei (= S. 66 und 67 des Skripts) wird gezeigt, wie die Dichte und die Gravitationsbeschleunigung der Erde in Abhängigkeit von der Tiefe aussieht, nach dem, was man heutzutage weiß und modellieren kann:
S. 72 unten:
"Die Schwerebeschleunigung hat im Mantel einen in etwa konstanten Wert und fällt im Kern mit steigender Tiefe linear ab."
Das zugehörige Diagramm auf Seite 73 ist aus dem Geophysik-Buch von G. C. Brown und A. E. Musset, The Inaccessible Earth, aus der Ausgabe von 1981. Ich habe es hier als Bild angehängt.
Wenn man in diesem Diagramm genau hinguckt, steigt der Wert von g in manchen Tiefen mit zunehmender Tiefe an; einmal ein kleines bisschen an der Erdoberfläche, und einmal etwas stärker in größerer Tiefe. Dazwischen fällt er ein bisschen ab, und im Kern fällt er stark und linear ab, bis er in der Mitte Null ist.
Gruß, Markus
| Beschreibung: |
|

Download |
| Dateiname: |
g von r der erde.gif |
| Dateigröße: |
19.39 KB |
| Heruntergeladen: |
8393 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. März 2006 21:58 Titel: dermarkus Verfasst am: 21. März 2006 21:58 Titel: |
 |
|
Lieber Opa, zum Hochladen von Bildern habe ich dir eine private Nachricht geschrieben. Du findest sie unter "Physikerboard" oben rechts bei deinen 'neuen Nachrichten'. 
----------------------------------------------------------------------
| Opa hat Folgendes geschrieben: | ...
Sir Isaac Newton, der jeden Satz Keplers belauschte, der sogar sein Minenspiel wie kein anderer kennt, wollte sich mit den letzten beiden Zeichnungen dann auch nicht mehr so richtig anfreunden. ... |
Das wundert mich ja ein bisschen, denn eigentlich müssten Newton die Schritte von 3B nach 3C und von 4B nach 4C besonders gefreut haben, da sie sein Gesetz der Gravitation in Reinform darstellen. Und auch beim Schritt von 4C nach 4D verwende ich sein Argument zur Begründung dessen, dass sich g bei diesem Schritt nicht verändert.
Und die anderen Schritte, nämlich das Hinzufügen und Wegnehmen von Massen, dürften Pierre Bouguer (1698-1758)(http://de.wikipedia.org/wiki/Pierre_Bouguer) sehr vertraut vorgekommen sein: Er wandte Newtons Gravitationstheorie auf die Dichteverteilungen an der Oberfläche der Erde an. Von ihm ist die Formel für die Korrektur durch die plattenförmigen Massen, die ich oben hergeleitet und verwendet habe.
Wenn man zusätzlich noch weiß, wie breit der Berg ist, dann kann man seine Berechnungen auch für Platten mit einem Radius kleiner als unendlich durchführen und die Formelbeschreibung verfeinern. Das ändert aber nichts am Vorzeichen der Effekte, wie sie in den Bildlein in 3 und 4 stehen.
|
|
 |
Gast
|
 Gast Verfasst am: 22. März 2006 01:34 Titel: Gast Verfasst am: 22. März 2006 01:34 Titel: |
 |
|
Gravitation bleibt mysteriös. Schwerkraft beschleunigt Massen, aber dazu muss Impuls übertragen werden. Der physikalische Mechanismus ist unerkannt, es gibt nur akzeptierte Formalismen zur Beschreibung der Wirkungen. Newton hat es abgelehnt, über die physikalischen Ursachen zu spekulieren und sich auf eine rein mathematische Abhandlung beschränkt. Er hat nur geäußert, dass er nicht an eine Fernwirkung glaube, denn das sei ein Rückfall in magisches, vorwissenschaftliches Denken. Sind wir heute, getarnt in verkrümmten neuen Kleidern aus Geometrie und Mathematik, dorthin zurückgekehrt? Oder ist die Suche schlicht aufgegeben worden?
> .. er [Newton] lehrte, daß die Gravitation überall in unserem Sonnensystem vorhanden ist.
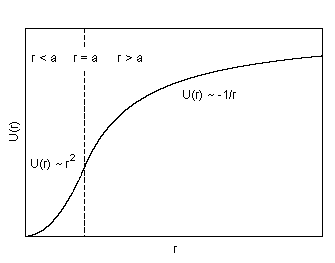
Ich habe die Sache mit den Uhren erwähnt um auf die beiden Aspekte des Gravitationsfeldes hinzuweisen: Gravitationsbeschleunigung und Gravitationspotential. Hiermit lässt sich das Rätsel lösen, warum trotz eines starken Feldes keine Schwerkraft wirkt im Innern des von Masse umgebenen Hohlraums (das war mit der 'massiven' Hohlkugel gemeint). Im Bild unten ist der Verlauf des Potentials in Relation zum Abstand vom Zentrum gezeigt, und zwar für eine Kugel mit überall gleicher Dichte, nicht vergleichbar mit der Erde. Die Schwerkraft bzw. Gravitationsbeschleunigung entspricht der Steigung der Kurve und man kann sehen, dass diese bei r = a (a ist der Radius der Kugel) den größten Wert hat und sich um diesen Punkt herum auch nicht stark ändert. Bei r = 0 (im Zentrum) ist sie null, ebenso für r -> unendlich. Das Potential hingegen steigt in Richtung Zentrum weiter an bis zum maximalen Wert (unten) und geht mit wachsendem Abstand von der Kugel gegen null (oben). Dieses Potential ist ein Maß für die Geschwindigkeit atomarer Wechselwirkungen und daher auch der Ganggeschwindigkeit von (Atom-) Uhren. Das Gravitationspotential gibt gewissermaßen an, wie 'tief' man im Feld steckt, also welche Arbeit aufzuwenden wäre, wenn man sich daraus ganz oder teilweise 'befreien' wollte.
Das andere Maß für die Ganggeschwindigkeit von Uhren ist übrigens ihre Geschwindigkeit im lokalen Gravitationsfeld (nicht aber die Beschleunigung), aber das ist ein anderes Thema.
Fortschritt kommt durch die Beantwortung von Fragen,
Entdeckungen hingegen durch das Befragen der Antworten.
| Beschreibung: |
|
| Dateigröße: |
1.65 KB |
| Angeschaut: |
79914 mal |
|
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 22. März 2006 04:48 Titel: am nechsten seind Opa Verfasst am: 22. März 2006 04:48 Titel: am nechsten seind |
 |
|
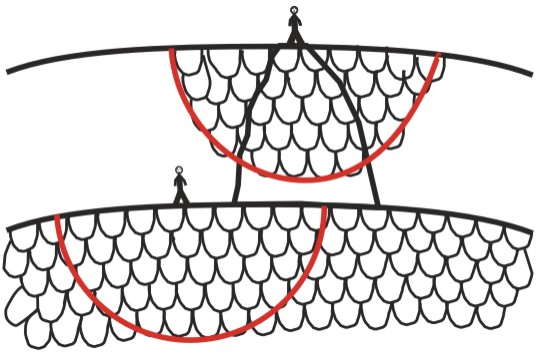
Die folgende Zeichnung soll zweierlei verdeutlichen
1. Keplers Satz „... das macht die anziehende gewalt der Erden, die steckht
nit im Centro
sondern im gantzen leib,
und ziehen diejenige stuckh am maisten,
die dem auffgeworffenen stain am nechsten seind.“
2. Oben auf dem Berg wird man leichter, weil weniger Massenstücke ziehen als unten.
Denn die Halbkreis-Massenstücke rechts und links vom Berge kann man sich wegdenken.
| Beschreibung: |
|
| Dateigröße: |
48.55 KB |
| Angeschaut: |
79886 mal |
|
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 22. März 2006 06:40 Titel: Opa Verfasst am: 22. März 2006 06:40 Titel: |
 |
|
Die nächste Zeichnung aus Wagenscheins Buch erläutert Keplers
(die fallenden Steine) ...„begehren nit des Orts, wie Aristoteles will, sondern nur des leibes.“
Links Aristoteles; rechts dagegen einige (wenige nur) Repräsentanten der Zugkräfte.
Links ein leeres geometrisches Schema (Wagenschein);
rechts wird das Männlein von jeder Scholle des Erdleibes gehalten.
| Beschreibung: |
|

Download |
| Dateiname: |
Wag39.jpg |
| Dateigröße: |
29.99 KB |
| Heruntergeladen: |
7588 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 22. März 2006 12:24 Titel: dermarkus Verfasst am: 22. März 2006 12:24 Titel: |
 |
|
Vorneweg:
Diese schönen Bilder und das Stirnrunzeln wichtiger Leute haben mich dazu bewogen, meine Bildlein oben ein bisschen übersichtlicher zu malen. Die verschönerte Version findet sich nun oben anstelle der alten.
------------------------------------------------
Mit diesen schönen Bildlein verstehe ich nun viel besser, was Wagenschein meint! Mit seinem zweiten Bild bin ich voll und ganz einverstanden. Genau mit solch einer Vorstellung habe ich gearbeitet, als ich die Massenanziehungskräfte der vielen einzelnen Massenpunkte berechnet und mit einem Integral zusammengezählt habe, um die Formel für die Bouguer-Korrektur herzuleiten.
Sein zweites Bild ist eine schöne klare Möglichkeit, in einem einzigen kleinen Bildlein zu zeigen, dass man auf dem Berg leichter wird (unter der Annahme, dass die Dichte des Berges nicht wesentlich anders ist als die Dichte des Bodens direkt darunter; diese Annahme halte ich für durchaus realistisch). Für diese elegante Reduktion des Problems auf diesen einfachen und klar durchschaubaren Teilaspekt hat nun auch er ein Lob verdient, für gutes didaktisches Erklären! Denn er hat erkannt, dass eine ausführlichere und detailliertere Betrachtung, wie sie Geophysiker von heute durchführen, nicht nötig ist, um das zu verdeutlichen, was er sagen wollte ("oben auf dem Berg ist man leichter").
Sein Schritt in seinem Bild ist also der in meinem Bild unten von 3Ca nach 3D. Geophysiker, die erklären wollen, dass man nicht nur auf einem Berg, sondern auch auf einer flachen Hochebene leichter ist als unten, und die richtig vorhersagen und berechnen wollen, wie groß der Effekt ist, müssen allerdings die Schritte 3A bis 3Ca vorneweg auch noch mitberücksichtigen. Und wenn sie die Gravitationsbeschleunigung mit ihren Gravimetern (das sind heutzutage genaue Federpendel, die klein genug sind, um gut transportabel zu sein) messen und mit ihren Rechnungen vergleichen, können sie damit über die Dichte des Gesteins unter ihnen Informationen gewinnen und damit auf die Art des Gesteins schließen.
Ich stimme Gast zu, dass laut der allgemeinen Relativitätstheorie Uhren im größeren Gravitationspotential langsamer gehen, und bin einverstanden mit seiner schönen Darstellung des Gravitationspotentials U(r) einer homogenen Kugel. Ich würde die Gravitation heutzutage allerdings vielleicht weniger als mystisch, sondern eher als spannend betrachten: Obwohl wir schon alle Experimente mit Gravitation, die wir bisher durchführen können, mit Newtons Gravitationstheorie oder Einsteins allgemeiner Relativitätstheorie beschreiben und ihre Ergebnisse vorhersagen können, bleiben experimentell ungeklärte Fragen wie zum Beispiel die Ausbreitungsgeschwindigkeit der Gravitationswechselwirkung.
| Gast hat Folgendes geschrieben: | Oder ist die Suche schlicht aufgegeben worden?
|
Keineswegs, denn Physiker sind ja schließlich neugierig  An einem experimentellen Nachweis von Gravitationswellen (siehe zum Beispiel http://www.physikerboard.de/htopic,4200,gravitationswellen.html und den dortigen Link zu Gravitationswellen) wird heute intensiv geforscht. An einem experimentellen Nachweis von Gravitationswellen (siehe zum Beispiel http://www.physikerboard.de/htopic,4200,gravitationswellen.html und den dortigen Link zu Gravitationswellen) wird heute intensiv geforscht.
| Beschreibung: |
|

Download |
| Dateiname: |
schwererleichter_wagenscheinvergleich.gif |
| Dateigröße: |
2.64 KB |
| Heruntergeladen: |
6958 mal |
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 22. März 2006 18:28 Titel: am nechsten seind Opa Verfasst am: 22. März 2006 18:28 Titel: am nechsten seind |
 |
|
>> Ich würde sagen, da hat Opa mit scharfem Auge eine Ungenauigkeit in der Wikipedia entdeckt. <<
Kann es nicht sein, daß hier jemand irrt und die beiden Sätze in Wikipedia korrekt sind?
Nebenbei:
In Wagenscheins Zeichnung links der „Aristoteles“ läßt sich recht gut auch zur Darstellung des Weltbildes des Aristoteles und der Antike benutzen, des klassischen geozentrischen Systems.
Man denke das Männlein und den Pfeil weg. Der kleine Kreis in der Mitte sei nun die Erde im Mittelpunkt des Weltalls. Man denke sich noch einige konzentrische Kreise hinzu, auf dem ersten kleinsten läuft der Mond um die Erde herum, dann Merkur, Venus, Sonne, Mars, Jupiter, Saturn. An den vorhandenen letzten Kreis hefte man noch ein paar Fixsterne an. Nun ist alles auf die Erde als Mittelpunkt des Weltalls bezogen.
Was brachte dieses Weltbild zum Einsturz?
Na, das war wohl die Entdeckung der Jupitermonde, die um den Jupiter herumlaufen, also nicht um die Erde, nicht um den Mittelpunkt der Welt.
Man zeichne einen kleinen Kreis, den Jupiter, mit ein paar Pünktchen drumherum ein ins „leere Schema“, zwischen Erde und Fixsternhimmel.
Wagenschein: „Für die Jupitermonde ist nicht der Mittelpunkt der Welt der Ort um den sie kreisen. Es ist ihr Jupiter, der ja nicht in der Weltenmitte sitzen kann, wenn wir es tun.
Er kann ihr Regent nur sein vermittelst seiner Materialität, Körperhaftigkeit, Leibhaftigkeit.
Und sie sitzt überall in ihm, nicht gerade im Mittelpunkt.“
Kepler: „...die steckht nit im Centro, sondern im ganzen leib, und ziehen diejenige stuckh am maisten, die dem auffgeworffenen stain am nechsten seind“.
Es gibt offenbar Zugkräfte zwischen Jupiter und seinen Monden, den aufgeworfenen Steinen, genau wie es Zugkräfte zwischen Eulers Attraktions-Berg in Amerika und einem daneben gehaltenen Lot gibt.
Das alles aber darf nach antikem Weltbild nicht sein, denn da steht die Erde im Mittelpunkt.
(Und auf der Erde konzentrierte sich alles auf den Mittelpunkt der Erde hin).
Gewiß, man kann, wenn man will, mit Hilfe der Integralrechnung, die übrigens Keppler nebenbei erfand, vorgehen, und alle Massenschollen der Erde rein rechnerisch zu einem einzigen Wert zusammenzählen und diese Kraft dann als theoretisch im Erdmittelpunkt sitzend weiter verwenden in Rechnungen. - Kepler erfand die Integralrechnung nebenbei, als er vermutete, sein Winzer würde ihn betrügen bei der Angabe des Inhaltes von Wein in einem Faß. Er steckte einen Stab ins Faß hinein, dann hatte er’s.
Newton baute dann Keplers Ansatz zur Formel aus. -
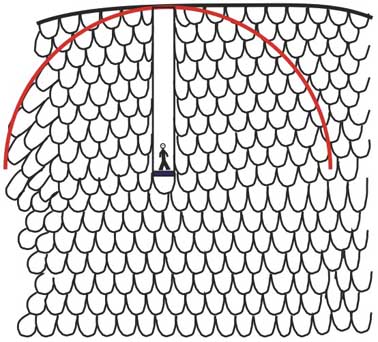
Wagenscheins zweite Zeichnung mit den Massenschollen führt vielleicht weiter, wenn das Männlein, immer gehalten von den Zugkräften aller einzelnen Massen, nun, sagen wir 500 Meter, in die Erde hineinfährt.
Diesen Fall des Leichterwerdens soll die folgende Zeichnung verdeutlichen. Es sind die Massenstücke über dem Kopf, die nach oben ziehen. Man kann sie vielleicht vage mit den Leibeskräften Jupiters vergleichen, die einen seiner Monde (das Männlein) an sich binden?!
| Beschreibung: |
|
| Dateigröße: |
49.68 KB |
| Angeschaut: |
79368 mal |
|
|
|
 |
Gast
|
 Gast Verfasst am: 22. März 2006 23:12 Titel: Gast Verfasst am: 22. März 2006 23:12 Titel: |
 |
|
> Man kann sie vielleicht vage mit den Leibeskräften Jupiters vergleichen,
die einen seiner Monde (das Männlein) an sich binden?!
Aber nur sehr vage, denn innerhalb einer Masse gelten eben andere Regeln als außerhalb.
Ist denn bei Wagenschein überhaupt von Masseverteilung oder Dichteverlauf die Rede, oder
geht er, vielleicht unausgesprochen, von einer homogenen Erde aus, und will lediglich die
prinzipiellen, also idealisierten, Zusammenhänge darstellen?
In der Realität steckt oft der 'Teufel' im Detail, aber das habe ich ja schon ausgeführt.
Und wenn das erstaunliche Diagramm das Markus gezeigt hat zutrifft, dann war mein Modell
aus Schaumstoff ja eher noch eine Untertreibung: In 3 km Tiefe würde man danach etwa 10%
schwerer sein als hier oben, und erst danach würde man leichter. Faszinierend...
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 23. März 2006 01:03 Titel: Re: am nechsten seind dermarkus Verfasst am: 23. März 2006 01:03 Titel: Re: am nechsten seind |
 |
|
| Opa hat Folgendes geschrieben: |
Kann es nicht sein, daß hier jemand irrt und die beiden Sätze in Wikipedia korrekt sind?
|
Die Wikipedia ist eine sehr demokratische Angelegenheit. Wenn man ihr etwas vernünftig begründetes sagt, dann berücksichtigt sie es in aller Regel sehr gerne. Der Satz "Das gilt auch für die Erde" ist mittlerweile von dieser Wikipedia-Seite verschwunden, und von zwei weiteren Wikipedianern wurde diese Änderung gutgeheißen und feingeschliffen.
| Opa hat Folgendes geschrieben: |
Es sind die Massenstücke über dem Kopf, die nach oben ziehen. |
Einverstanden, diese Massenstücke ziehen nach oben. Und wenn das ganze in einem Berg stattfindet, dann wird man deshalb leichter. Ich nehme zu Wagenscheins Gunsten an, dass er mit seinem anschaulichen Bild dies gemeint hat.
Wenn das ganze unter Meereshöhe stattfindet, dann allerdings gilt Wagenscheins einfaches anschauliches Bild nicht mehr. Denn dann spielen auch die Massenstücke im restlichen Teil der Kugelschale (wie in Bild 4D ganze Erde gemalt) ein entscheidende, gewichtige Rolle. Sie können also nicht einfach bei der Überlegung vernachlässigt werden: Sie sind zwar viel weiter weg, aber eben auch zusammen viel mehr und daher viel schwerer, und zwar genau so, dass sie die Kraft der Massenschollen über dem Kopf laut Newtons Gravitationsgesetzen gerade aufheben. Dann wird man also beim Schritt von 4C ganze Erde nach 4D ganze Erde weder leichter noch schwerer. Das lässt sich in der Tat am besten mit dem Newtonschen Gravitationspotential erklären, wie Gast schon gesagt hat.
Wagenscheins Bilder sind also sehr anschaulich. Aber weil die Geophysiker heutzutage kein Problem haben, die Massenanziehungskräfte der Massenstückchen zusammenzuzählen und auszurechnen, und dabei auch zu berücksichtigen, wie groß die Dichte der verschiedenen Massenstückchen ist, und wie sich auch die Kräfte der weiter entfernten Massestückchen integrieren lassen, können sie schon viel genauer rechnen als Wagenscheins anschaulich und didaktisch vereinfachte Bilder. Sie brauchen also Wagenscheins Näherungen nicht, dass man sich die Erde der Einfachheit als homogene Kugel vorstellt und dass man die Wirkung aller weiter entfernten Massenstückchen vernachlässigt, weil sie vielleicht die Betrachtung komplizierter gestalten oder nicht mehr in die Zeichnung hineinpassen. Sondern sie berechnen die Erde mit allen ihren räumlichen Dichteunterschieden und vergleichen diese Rechnungen erfolgreich mit ihren präzisen Messungen.
Das Diagramm, was ich gezeigt habe, ist viel weniger erstaunlich, als Gast gemeint hat, weil die Zunahme von g um 10% nicht auf nur 3 km (das wäre in der Tat extrem!), sondern auf ganzen 3000 km, also etwa auf halben Weg bis zum Erdmittelpunkt, stattfindet, wie man bei genauem Betrachten der radialen Koordinatenachse sieht. Das hat also nichts mit Schaumstoff zu tun 
|
|
 |
Gast
|
 Gast Verfasst am: 23. März 2006 01:50 Titel: Gast Verfasst am: 23. März 2006 01:50 Titel: |
 |
|
3 km war Tippfehler, der halbe Erdradius war verstanden. Den Dichtesprung fand ich erstaunlich,
dort beginnt wohl der äußere Erdkern. Die Schaumstoffsache war ja auf die Erdkruste bezogen, dieser
Bereich ist im Diagramm nur mühsam zu erkennen, aber es scheint auch dort leicht aufwärts zu gehen.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 23. März 2006 02:11 Titel: dermarkus Verfasst am: 23. März 2006 02:11 Titel: |
 |
|
| Anonymous hat Folgendes geschrieben: | Den Dichtesprung fand ich erstaunlich,
dort beginnt wohl der äußere Erdkern. |
Stimmt, das passt auch zu deiner Wikipedia-Skizze vom Erdaufbau, nach der der äußere Erdkern bei 2900 km Tiefe beginnt.
|
|
 |
Opa
Anmeldungsdatum: 19.03.2006
Beiträge: 39
Wohnort: Bonn
|
 Opa Verfasst am: 23. März 2006 05:06 Titel: Opa Verfasst am: 23. März 2006 05:06 Titel: |
 |
|
> Ist denn bei Wagenschein überhaupt ......<
Wagenschein ging es um ursprüngliches Verstehen und exaktes Denken, so lautete einer seiner Buchtitel. Er war der Ansicht, etwa 95 Prozent der Abiturienten, Studenten und Erwachsenen hätten etwas im Kopfe, was er Bildungsschotter nannte, unverstandenes Pseudo-wissen. So wurde beispielsweise einmal von dem aus dem Fernsehen bekannt gewordenen Astronom Rudolf Kühn eine Umfrage unter den Besuchern seiner Sternwarte gemacht.
„Wie kommt es,“ so fragte er, „daß die Gestalt des Mondes vom Vollmond zum Halbmond, zur Sichel und zum Neumond wechselt?“ Etwa achtzig Prozent der befragten Besucher wußten keine richtige Antwort. Eine andere Umfrage ergab, daß etwa 25% der Studenten, dieselbe rasche, doch absurde Auskunft zur Hand haben: der Schatten unserer Erdkugel sei es; der mache den Mond immer wieder zur Sichel. Von Wagenscheins Studenten wurde anschließend diese Umfrage unterderhand und unsystematisch weiter durchgeführt. Sie ergab, daß in einem beliebigen Personenkreis ungefähr 50 % den Erdschatten verantwortlich machen. Opa gehörte auch dazu. Seitdem versucht er mühsam, seinen Bildungsschotter zu sortieren, ihn wegzuräumen und ganz einfache Erkenntnisse sich zu verschaffen.
Wie er das macht, geht aus seinen Beiträgen hervor: Er versucht, bei den großen Gelehrten nachzulesen. Zum Beispiel bei Galileo Galilei, den es manchmal in Antiquariaten gibt, in deutscher Übersetzung. Das erste echte Gesetz der neuzeitlichen Physik, sagen einige, das sei das Fallgesetz. In der Schule wurde es mir beigebracht mit s = ½ g t². Galilei aber kannte kein s, kein g und kein t, diese Formelsprache gab es nicht, er mußte mit der normalen Sprache ausdrücken, was er gefunden hatte. Wie heißt es bei ihm?
„Man sieht also, ... daß ... die in gleichen Zeiten durchlaufenen Wege sich wie die ungeraden Zahlen 1, 3, 5 ... verhalten. ...“.
Wie sah seine Versuchsanordnung aus, wie hat er die Zeit gemessen?
Das sind die eigentlich interessanten Fragen, aus denen heraus sich ein ursprüngliches Verstehen entwickeln kann. Aus einer schnell gelernten Formel wie ½ g t Quadrat aber entwickelt sich nichts. Wagenschein nennt sie eine Scheinblüte, eine Papierblume.
> 10% schwerer < unter Tage, hat das was mit dem Weltmodell der Pythagoräer zu tun, die wegen der heiligen Zahl 10 zu den acht „Planetensphären“ noch ein Zentralfeuer und eine berühmte Gegenerde kannten, die beide man leider nicht sehen konnte, weil man auf der ihnen abgewandten Seite lebte?
Das Schaumstoffmodell kam mir auch als Untertreibung vor, ist es doch aufschlußreich und gewiß extrem faszinierend ...
> In der Realität steckt oft der 'Teufel' im Detail <
Ja der alte Diabolos, was kann der nicht alles durcheinanderwerfen, wohl gar auch die verschiedenen Dichten im Schaumstoff, gewiß aber die Realität, wenn’s eine solche jemals gibt. - Eigentlich müßte man mit einem Wasserwürfel von einem Meter Kantenlänge 3 km tief in den Bergwerksschacht einfahren und ihn dort wiegen, um die strittige Frage per Versuch entscheiden zu können. Doch wer macht’s.
Opa hat noch eine ‚teuflische’, gleichwohl ziemlich formelfreie Frage:
Tycho Brahe, der Mann mit der goldenen Ersatznase, Keplers Vorgänger in Prag, sogar einen Krater auf dem Mond hat man nach ihm benannt, behauptete etwa:
Die Erde dreht sich einmal am Tag herum. (Das macht heute ungefähr 40 000 km / 24 / 60 / 60 = 0,462 km pro Sekunde, am Äquator etwa). Wenn nun ein Apfel vom Baum fällt, dann dreht sich die Erde unter ihm weg, so Tycho. Dauert der Fall nun 1 Sekunde, dann würde der Apfel gut 400 Meter vom Baum entfernt in Nachbars Garten landen. (So weit ging Tycho allerdings nicht, doch immerhin ließ er den Apfel nicht senkrecht fallen, sondern ein paar Millimeter weg von der Senkrechten, links, weil die Erde sich weitergedreht hatte. Wohin fällt der Apfel, etwas nach links, genau senkrecht oder etwas nach rechts?
|
|
 |
Gast
|
 Gast Verfasst am: 23. März 2006 11:44 Titel: Gast Verfasst am: 23. März 2006 11:44 Titel: |
 |
|
> Wohin fällt der Apfel, etwas nach links, genau senkrecht oder etwas nach rechts?
Links und rechts sind relative Richtungen, sie sind nur bestimmt wenn man weiß, wo vorn ist,
oben und unten ergeben sich auf der Erde 'von selbst'. In diesem Fall ist es besser, eindeutige
Richtungen zu verwenden, also Osten und Westen. Der Apfel am Baum bewegt sich schneller nach
Osten, als der Boden unter ihm, denn in einem rotierenden Gebilde hängt die Bahngeschwindigkeit
eines Ortes von seinem Abstand vom Drehzentrum ab, hier der Erdmitte.
Sobald man diesen Gedanken realisiert hat, ist die Antwort rein deduktiv zu bekommen, man kann
den Vorgang beschreiben als einen waagerechten Wurf aus der Höhe h des Apfels, und das mit einer
Startgeschwindigkeit, die dem Zuwachs der Bahngeschwindigkeit bei Höhe h gegenüber der Höhe null
am Boden entspricht. Der waagerechte Wurf hat zwei Komponenten, einmal den freien Fall aus h, und
gleichzeitig eine horizontale Bewegung mit konstanter Geschwindigkeit, von allen Widrigkeiten ist
aber dabei abgesehen, ganz im Sinne Wagenscheins, nur der pure Effekt wird beschrieben, und auch
die Kreisbahn wird wegen des riesigen Radius hier gerade gebogen.
Überlagert man diese beiden Bewegungen, also die beschleunigte nach unten und die konstante nach
Osten, dann gelangt man zu einer beschreibenden Gleichung, die den Versatz des Apfels gegenüber
dem Punkt lotrecht unter dem Startort angibt. Die Zeit für den ganzen Vorgang bekommt man aus der
für den Fall, und der horizontale Weg ist dann die beschriebene Startgeschwindigkeit mal der Zeit.
Würde man einen 50 m hohen Apfelbaum am Äquator finden, dann würde der Apfel knapp 12 mm versetzt
in Richtung Osten auf dem Boden ankommen. Aber nur ohne Luft dazwischen, denn der Teufel steckt
auch hier wieder mal im Detail.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 23. März 2006 11:55 Titel: dermarkus Verfasst am: 23. März 2006 11:55 Titel: |
 |
|
| Opa hat Folgendes geschrieben: |
Die Erde dreht sich einmal am Tag herum. (Das macht heute ungefähr 40 000 km / 24 / 60 / 60 = 0,462 km pro Sekunde, am Äquator etwa). Wenn nun ein Apfel vom Baum fällt, dann dreht sich die Erde unter ihm weg, so Tycho. Dauert der Fall nun 1 Sekunde, dann würde der Apfel gut 400 Meter vom Baum entfernt in Nachbars Garten landen. (So weit ging Tycho allerdings nicht, doch immerhin ließ er den Apfel nicht senkrecht fallen, sondern ein paar Millimeter weg von der Senkrechten, links, weil die Erde sich weitergedreht hatte. Wohin fällt der Apfel, etwas nach links, genau senkrecht oder etwas nach rechts? |
Das ist eine Textaufgabe zum Thema Corioliskraft. Der Apfel bewegt sich in der Tat nicht mit 460 m/s relativ zum Erdboden, und zwar weil er ja zu Beginn am Baum hängt und sich mit der Erde mitbewegt. Würde sich die Erdoberfläche geradlinig weiterbewegen, während er fällt, dann würde er also genau senkrecht herunterfallen. Nun dreht sich aber die Erde, und die Erdoberfläche bewegt sich auf einer Kreisbahn. Der Apfel hingegen flöge ohne Schwerkraft geradeaus weiter.
Für den fallenden Apfel bedeutet das, dass er deshalb ein Stückchen vor der sich nach Osten drehenden Erde vorauseilt. Einige Millimeter sind allerdings stark übertrieben. Wenn ich die Größe des Effekts mit Formeln berechne, dann trifft der Apfel am Äquator lediglich 240 Mikrometer (also rund einen Viertelmillimeter) weiter östlich auf als bei einem genau senkrechten Fall.
// edit: Sorry, dass ich hier sowohl die Richtung als auch die Größe des Effekts korrigieren musste, weil ich bei den Ergebnissen, die ich zuerst hier angegeben hatte, Fehler gemacht habe. Sollte die komplette, nun richtige Rechnung von Interesse sein, so sage man das bitte, dann gebe ich sie gerne an.
Zuletzt bearbeitet von dermarkus am 23. März 2006 21:42, insgesamt einmal bearbeitet |
|
 |
|
|
















 Kann mir bitte jemand helfen?
Kann mir bitte jemand helfen? 


 )
)


