| Autor |
Nachricht |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 18. Dez 2009 20:48 Titel: Trägheitstensor eines 2-dim. Körpers Airblader Verfasst am: 18. Dez 2009 20:48 Titel: Trägheitstensor eines 2-dim. Körpers |
 |
|
Hi,
mit den Trägheitsmomenten und -körpern stehe ich zur Zeit echt auf Kriegsfuß. So langsam verstehe ich immer mehr, aber irgendwie auch immer weniger.
Es geht um Folgendes:
Durch die Punkte A(-3, -0.5), B(1, -0.5) und C(1, 1.5) sei ein Dreieck gegeben, das vernachlässigbar dünn ein Prisma homogener Dichte ist.
Zu Berechnen sind Schwerpunkt und "Trägheitstensor  in der xy-Ebene (Drehachsen entlang der Koordinatenachsen". in der xy-Ebene (Drehachsen entlang der Koordinatenachsen".
Den Schwerpunkt habe ich hinbekommen, doch beim Tensor hängt es. Und zwar zuerstmal mit dem Verständnis.
Wie wird denn um beide Achsen gedreht? Oder verstehe ich das falsch? In einem Beispiel mit gleichem Wortlaut kommt ein 2x2-Tensor heraus, also schätze ich, wird um die z-Achse gedreht, so dass der Körper immer in der xy-Ebene bleibt.
Ich habe dann einen Tensor 2. Stufe in der bekannten Form und damit habe ich 6 Integrale zu berechnen.
Nehmen wir als Beispiel doch einfach mal das Erste:
\dd m)
Wie habe ich dann hier vorzugehen? r ist ja der senkrechte Abstand von der Drehachse (z-Achse(?)).
Ich muss also erstmal das dm ersetzen, und würde das mit  tun (Rho ist hier eben eine Flächendichte). tun (Rho ist hier eben eine Flächendichte).
Aber wie habe ich die Grenzen zu wählen? Was genau sag mir überhaupt die xx-te oder xy-te (...) Komponente des Tensors? Und was ist mit dem r?
Und ist es überhaupt alles richtig? Irgendwie habe ich das Gefühl, die Drehachse müsste im Schwerpunkt liegen, denn eigentlich hatten wir es nur immer so.
Wie man sieht bin ich etwas überfragt und es wäre schön, wenn mir jemand ein paar Tipps geben könnte. Es wird Zeit, dass ich das hinbekomme. 
Danke schonmal!
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 18. Dez 2009 23:10 Titel: bishop Verfasst am: 18. Dez 2009 23:10 Titel: |
 |
|
Oh Gott, Theo I ist bei mir schon wieder eine Weile her aber ich versuche dir möglichst gut zu helfen ^^
Wie der Wiki Artikel schon sagt geht es eigetlich nur darum die Integrationsgrenzen sauber hinzubekommen und bei krummen Körpern geht das dadurch, dass man eine Grenze als Variable auffasst, das heisst du hast dann integrale der art }f(x)dx\cdot\int~f(y)dy)
Du integrierst dann über dx und bekommst als einen Vorfaktor irgendeine Funktion in y, weil deine Grenzen hier variabel angesetzt wurden. Dann integrierst du diese und all den Rest, den du vielleicht vorher hattest über dy und hast dein Ergebnis!
Versuche dich doch mal an der folgenden Übungsaufgabe:
Berechne den Flächeninhalt eines Dreiecks mit den Eckpunkten (0,0), (0,a) und (b,0)
Versuche tatsächlich das Flächenintegral auszuführen, wenn du nicht klarkommst überlege ich mir wie man dich auf den Gedanken stoßen kann ohne alles vorwegzunehmen -.-
hoffe das hat etwas geholfen
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 18. Dez 2009 23:27 Titel: Airblader Verfasst am: 18. Dez 2009 23:27 Titel: |
 |
|
Das Flächenintegral wäre/ist kein Problem, das bekomme ich hin. Aber bei den Grenzen im obigen Beispiel habe ich Probleme.
Außerdem weiß ich nicht so recht mit dem r umzugehen. Geschweige denn, ob villt. sogar alles falsch ist.
Edit: Noch als Anmerkung ... steht das Integral da, habe ich auch kein Problem, es zu berechnen. Mir geht es darum, von dem Integral, das ich oben nannte (Komponennte des Tensors) auf eine Form zu kommen, die man dann berechnet.
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 19. Dez 2009 19:16 Titel: bishop Verfasst am: 19. Dez 2009 19:16 Titel: |
 |
|
naja das r ist das Übliche  , was die Hauptträgheitsmomente immer die Form von z.B , was die Hauptträgheitsmomente immer die Form von z.B  annehmen lässt. annehmen lässt.
Mehr fällt mir grad nicht sinnvolles ein, es ist einfach Übungssache die Grenzen zu finden, vielleicht hat jemand anderes was intelligenteres zu sagen als ich zu dem Thema -.-
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 19. Dez 2009 20:21 Titel: Airblader Verfasst am: 19. Dez 2009 20:21 Titel: |
 |
|
Das wäre toll. Aber Danke schonmal für deine Mühe!
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 20. Dez 2009 00:22 Titel: MI Verfasst am: 20. Dez 2009 00:22 Titel: |
 |
|
Hier meine Überlegungen zum Thema:
Wenn ich mir das recht überlege, sollte es doch möglich sein, einfach ein geeignetes Koordinatensystem zu wählen, wo man die Grenzen gut finden kann und dann entsprechend einen Basiswechsel vorzunehmen, um den Trägheitstensor in der gegebenen Basis zu finden.
Nichts anderes macht man ja bei der Suche der Hauptträgheitsachsen (d.h.: der Achsen, die als Drehachsen stabil sind)
r ist dabei aber nicht der senkrechte Abstand zur Drehachse, sondern der Ortspunkt.
Der Trägheitstensor sollte ja nicht von der Drehachse abhängen - sonst könnte man ja auch einfach die Trägheit bzgl. der Drehachse angeben. Vielmehr kannst du z.B. den Drehimpuls bzgl. BELIEBIGER Drehachsen (durch den Ursprung des Koordinatensystems!) mit dem Trägheitstensor angeben.
Gruß
MI |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 01:17 Titel: Airblader Verfasst am: 20. Dez 2009 01:17 Titel: |
 |
|
Ah - das mit dem r erklärt dann ja mal einiges.
Mit den Drehachsen ... nun ... direkt in der Teilaufgabe danach soll ich den Tensor erneut berechnen, dann aber "Verlauf der Drehachsen durch den Schwerpunkt, parallel zu den Koordinatenachsen".
Also muss da ja doch irgendwas mitspielen?
Was mich auch wundert, ist, dass wir den Tensor bisher immer nur bei der Drehung um eine Achse durch den Schwerpunkt betrachtet hatten und er es nun bei Aufgabe a) nicht so ist - und ich absolut überfragt bin, was sich dabei ändert.
Der geringe Anklang ist momentan fast schade. Ich finde es supernett, dass man versucht, zu helfen, wirklich. Aber ist denn niemand unterwegs, der sich nicht selbst erst groß reinarbeiten muss?
Das Ganze kommt aus der ExPhys I, sollte doch also für viele Leute kein größeres Problem darstellen (?).
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 01:55 Titel: dermarkus Verfasst am: 20. Dez 2009 01:55 Titel: |
 |
|
Das Trägheitsmoment ist ja die Summe der Trägheitsmomente aller Massenelemente m_i:

dabei ist  die Masse eines Massenelementes, und die Masse eines Massenelementes, und 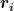 ist der Abstand dieses Massenelementes von der Drehachse. ist der Abstand dieses Massenelementes von der Drehachse.
Für das Hinschreiben eines Integrales zum Beispiel für das Drehmoment bezüglich der y-Achse als Drehachse ist dieser Abstand der Massenelemente von der Drehachse nichts anderes als die x-Kompenente des jeweiligen Punktes (genaugenommen ihr Betrag, aber das macht ja wegen dem Quadrat hier keinen Unterschied).
Das die Grenzen des Integrals über y hängen dabei von x ab, die Geradengleichung x) für die obere dieser Grenzen bekommt man am leichtesten, wenn man sich das Dreieck laut Aufgabenstellung mal aufmalt. für die obere dieser Grenzen bekommt man am leichtesten, wenn man sich das Dreieck laut Aufgabenstellung mal aufmalt.
Damit bekomme ich für das Trägheitsmoment 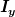 bezüglich der y-Achse: (Als Dichte verwende ich hier der Einfachheit halber die Flächendichte, die ich hier mal bezüglich der y-Achse: (Als Dichte verwende ich hier der Einfachheit halber die Flächendichte, die ich hier mal 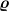 nenne, und integriere über die Fläche, da die Integration über z in diesem Fall sowieso nur eine Multiplikation mit der Prismendicke darstellen würde.) nenne, und integriere über die Fläche, da die Integration über z in diesem Fall sowieso nur eine Multiplikation mit der Prismendicke darstellen würde.)
x} x^2 \, \dd y \, \dd x
<br />
)
Um das auszurechnen, löst man dann natürlich zuerst das innere Integral, also das über y. Wird damit dann schon klar, wie das hier geht?
Ich denke, die beiden Achsen, bezüglich derer man laut Aufgabenstellung das Trägheitsmoment ausrechnen soll, werden die y-Achse sowie die x-Achse sein.
Zuletzt bearbeitet von dermarkus am 20. Dez 2009 03:36, insgesamt einmal bearbeitet |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 20. Dez 2009 02:20 Titel: MI Verfasst am: 20. Dez 2009 02:20 Titel: |
 |
|
Ah, okay, es geht um Ex I. Dann ist mein Ansatz über den Trägheisttensor und Basiswechsel, etc. pp. ein wohl etwas zu komplizierter Ansatz für das Problem  . .
Wenn es im Grunde wirklich nur um die Drehmomente bzgl. bestimmter Achsen geht, dann hat dermarkus schon alles gesagt - das würde auch erklären, warum in der Aufgabenstellung die Drehachsen explizit angegeben sind.
Im Fall zeitlich konstanter, fest vorgegebener Drehachsen lohnt es sich nicht, den Trägheitstensor auszurechnen. Dieser ist vorwiegend dann interessant, wenn sich die Drehachse im körperfesten Koordinatensystem ständig ändert, also z.B. bei Kreiselbewegungen mit Nutation und Präzession.
Wir haben daher in der Ex I zum Beispiel den Trägheitstensor mehr oder weniger nur definiert. Wirklich gerechnet haben wir damit nicht und an vielen anderen Unis wird das ähnlich sein. Daher sind sowohl bishop, als auch ich davon ausgegangen es handele sich um theoretische Physik.
Gruß
MI |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 11:53 Titel: Airblader Verfasst am: 20. Dez 2009 11:53 Titel: |
 |
|
@ MI
Gut, das erklärt natürlich ein paar Dinge.
In der Vorlesung haben wir den auch kein einziges Mal "per Hand" ausgerechnet, sondern gleich gesagt, dass es eine Aufgabe für Matlab ist. Im Übungsblatt jedoch müssen wir zwei Tensoren per Hand berechnen, dann gehts mit Matlab los.
Mir geht es ja aber auch um das Verständnis.
@ dermarkus
Das Trägheitsmoment ist, denke ich, kein Problem, wäre mir soweit also klar.
Mit I_y meinst du ja das Moment bzgl. Drehung um die y-Achse. Wie sind dann die Komponenten des Tensors zu deuten, also I_xx oder I_xy, ...?
Das Problem ist ja, dass ich gar nicht so recht weiß, um was ich bei diesen Komponenten d. Tensors überhaupt drehe und daraus resultiert auch, dass ich keine Ahnung habe, wie ich die Grenzen zu wähle habe.
Zu guter letzt: Was hat der Schwerpunkt mit dem Zeug zu tun? Wir haben den Tensor hergeleitet unter dem Gesichtspunkt, die Drehachse läuft durch den Schwerpunkt.
Das tut sie hier ja nicht, und die nächste Aufgabe ist es, den Tensor eben zu berechnen, wenn man um die Achse durch den Schwerpunkt dreht. Aber was ändert sich dann, bzw. eher was ändert sich jetzt, wo ich das noch nicht mache?
Danke schonmal für die Antworten!
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 15:25 Titel: dermarkus Verfasst am: 20. Dez 2009 15:25 Titel: |
 |
|
Ich vermute, da hilft es am schnellsten weiter, sich in den Mitschrieben, Skripten und in Büchern nochmal anzuschauen, was ein Trägheitstensor ist.
Wenn ich mich recht erinnere, dann ist die I_yy - Komponente des Trägheitstensors das Trägheitsmoment des Körpers bezüglich der Achse, die parallel zur y-Achse verläuft und durch den Schwerpunkt des Körpers geht.
Und ich vermute, dass man dieses I_yy folglich aus dem I_y, das ich oben hingeschrieben habe, am einfachsten und schnellsten mit Hilfe des Satzes von Steiner bekommt.
Kommst du beim Nachschlagen zum Thema Trägheitstensor zum selben Ergebnis, und kommst du damit beim konkreten Rechnen voran / durch ? |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 15:55 Titel: Airblader Verfasst am: 20. Dez 2009 15:55 Titel: |
 |
|
Hi,
ich habe alle Aufschriebe, sowie Begleitmaterialien die wir bekommen haben natürlich mehrfach durchgelesen.
Allerdings haben wir den Tensor nur hergeleitet (und auch das ist nicht ganz klar), nie konkret einen berechnet. In den Begleitmerialien wurde tatsächlich einer berechnet, ebenfalls für ein Dreieck - aber eben mit Matlab und numerisch.
Google lief zwischenzeitlich auch schon heiß (Leute fragen ist für mich sowieso immer letzte Instanz), aber irgendwie finde ich da auch nie konkrete "per Hand"-Berechnungen der Integrale.
Deine Interpretation von I_yy klingt für mich allerdings völlig schlüssig. Bleibt die Frage, wie ich den Tensor hier aber zu handlen habe, nachdem die Drehachse eben nicht durch den Schwerpunkt geht.
Klar, mit Steiner kein Problem - aber sehen die Einträge des Tensors dann überhaupt so aus, mit diesen Integralen?
Lassen wir das "Problem" kurz beiseite, dann könnte ich durch die Trägheitsmomente schonmal problemlos schnell die Diagonaleinträge des Tensors berechnen.
Aber dann würden ja immer noch die anderen Integrale bleiben wie z.B. 
An sich würde ich ja, auch angesichts meiner AnaI-Klausur morgen, das Ganze sein lassen und mir in der Übung einfach anschauen - allerdings kann ich die Votierpunkte mehr als gut brauchen *seufz*. Zum Glück ist Ana I ein Kinderspiel.
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 16:12 Titel: dermarkus Verfasst am: 20. Dez 2009 16:12 Titel: |
 |
|
Ich bin einverstanden, dass die hier zu berechnenden Komponenten des Trägheitstensors I_xx, I_yy, I_xy und I_yx sein werden.
Wo liegt konkret noch das Problem bei der Berechnung der Nichtdiagonalelemente?
Meine Vermutung ist, man könnte zum Beispiel einfach den Koordinatenursprung im Schwerpunkt wählen, die Koordinatenachsen parallel zur x- achse und y-Achse.
Dann die Integrationsgrenzen wieder, soweit nötig, als Funktion y(x) aufstellen (das wird wieder nur die obere Grenze des Integrals für y betreffen), und auch in den Integralen für I_xy oder für I_yx wieder anfangen mit  und Integrale wieder so ausrechnen wie oben schon angedeutet. und Integrale wieder so ausrechnen wie oben schon angedeutet. |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 16:40 Titel: Airblader Verfasst am: 20. Dez 2009 16:40 Titel: |
 |
|
Hi,
erstmal zu der "Wahl des Nullpunktes":
Das riecht für mich irgendwie faul, denn wie gesagt:
Wir sollen diesen Tensor berechnen und in der nächsten Teilaufgabe dann nochmal, dann mit "Verlauf der Drehachsen durch den Schwerpunkt". Und genau das wäre jetzt ja dein Vorschlag.
Das ist aber also erst die nächste Aufgabe.
Zu den Nicht-Diagonalelementen:
Nun, bei I_yy hast du mir oben jetzt ja eine Interpretation geliefert. Aber die leuchtet mir nur für I_xx, I_yy und I_zz ein - doch wie erhalte ich I_xy u.ä.?
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 18:58 Titel: dermarkus Verfasst am: 20. Dez 2009 18:58 Titel: |
 |
|
Ach so, wenn du den gesamten Aufgabentext in so einer Form dastehen hast, dann ist sicher im ersten Schritt erstmal der Trägheitstensor bezogen auf den Koordinatenursprung gemeint. (dann vereinfacht es die Aufgabe erheblich, schlicht den vollständigen wörtlichen Aufgabentext dieser und der nächsten (Teil-?) Aufgaben zu kennen  ). ).
Hast du zur Berechnung der Nichtdiagonalelemente nicht oben (Beitrag von 3:55) schon eine Formel hingeschrieben, mit der du das direkt schon ausrechnen könntest? |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 19:38 Titel: Airblader Verfasst am: 20. Dez 2009 19:38 Titel: |
 |
|
Hi,
nunja - da steht eben das Integral. Aber wie gesagt .. weder weiß ich, ob ich dieses nehmen "darf" (bzw. den ganzen Tensor der so aussieht), da die Drehachse ja nicht durchden Schwerpunkt geht, noch würde es mir helfen, da ich hier dann wieder keine Ahnung hätte, welche Grenzen zu verwenden sind.
Bei den Diagonaleinträgen wüsste ich das, dank dir, zwischenzeitlich ja.
Hier mal der Aufgabentext:
| Zitat: | a) Berechnen Sie den Schwerpunkt des Dreiecks und den Trägheitstensor  in der xy-Ebene (Drehachsen entlang den Koordinatenachsen). in der xy-Ebene (Drehachsen entlang den Koordinatenachsen).
b) Berechnen Sie den Trägheitstensor  bei Verlauf der Drehachsen durch den Schwerpunkt, parallel zu den Koordinatenachsen bei Verlauf der Drehachsen durch den Schwerpunkt, parallel zu den Koordinatenachsen |
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 19:46 Titel: dermarkus Verfasst am: 20. Dez 2009 19:46 Titel: |
 |
|
Okay, dann sieht das in der Tat gut aus, dann wird der Weg, den wir nun haben, der richtige sein 
Magst du mal eines dieser Diagonalelemente komplett als Integral hinschreiben und schauen, ob du es mit dem, was du nun eigentlich schon alles beieinander haben dürftest, schon ausrechnen kannst?
Ich glaube, einer der größten Fortschritte beider Berechnung solcher Integrale, wie sie bei der Berechnung von Trägheitsmomenten und so vorkommen, ist, mal erfolgreich ein paar davon ausgerechnet zu haben und erlebt zu haben, wie radikal einfach die Ausdrücke sind, die dabei jeweils am Ende rauskommen  |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 20:03 Titel: Airblader Verfasst am: 20. Dez 2009 20:03 Titel: |
 |
|
Ich würde liebend gerne die Integrale d. Diagonalelemente berechnen - sobald ich auch weiß, was die darstellen und wie ich an die Grenzen komme.
Denn ohne dieses Wissen ist es recht langweilig:

Wie gesagt - bei den Diagonalelementen bin ich ja "weiter". Da weiß ich: Ich nehme das Trägheitsmoment und verschiebe mit Steiner dann in den Schwerpunkt.
Wobei mir da gerade auffällt: Wäre das dann nicht auch schon wieder Aufgabenteil (b) ?
Irgendwie macht das Tensorenkonzept für mich einfach keinen Sinn, wenn die Achse nicht durch den Schwerpunkt geht, weil wir das Ding ja so eingeführt haben.
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 20:25 Titel: dermarkus Verfasst am: 20. Dez 2009 20:25 Titel: |
 |
|
|
Na, wie die Integrationsgrenzen für dieses Dreieck sind (und in welcher Reihenfolge man hier praktischerweise über y und über x integriert), habe ich ja schon oben schonmal fertig hingeschrieben, das kannst du einfach wieder so verwenden. |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 20:28 Titel: Airblader Verfasst am: 20. Dez 2009 20:28 Titel: |
 |
|
Sind die für alle Einträge des Tensors denn gleich?
Ich meine, bei I_xx und I_yy dürften sie doch auch schon anders sein, da man einmal um x- und einmal um x-Achse das Trägheitsmoment berechnet (und dann verschiebt*), oder?
*) Und wie gesagt - für mich klingt das irgendwie widersprüchlich, weil man dann ja sozusagen Aufgabe b) berechnet, nicht a).
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 20:36 Titel: dermarkus Verfasst am: 20. Dez 2009 20:36 Titel: |
 |
|
* Die Integrationsgrenzen sind für alle Elemente gleich, denn du integrierst ja jeweils über das gleiche Dreieck.
* erstmal a) rechnen, also ohne Verschieben.
* Für I_xx ist der Abstand zur x-Achse im Quadrat dann natürlich y^2 (statt x^2 wie in den Integralen für I_yy).
* Magst du mal anfangen, eines der Elemente für den a) Teil komplett hinzuschreiben und auszurechnen? Manchmal hilft konkretes Gerechnet-Haben schon viel beim Überblick-Gewinnen und verstehen  |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 20:53 Titel: Airblader Verfasst am: 20. Dez 2009 20:53 Titel: |
 |
|
Hi,
okay - dass die Grenzen gleich sind war mir absolut nicht klar. Das macht es auch erheblich einfacher.
Ich beschränke mich einfach mal auf zwei Integrale:
Einmal ein Diagonalelement:
~\dd x = 4\varrho)
Und dann ein nicht-Diagonalelement:

Allerdings will ich gleich nochmal was einwerfen:
Das Integral lautet doch eig. \dd m = \int~(y^2+z^2)\dd m) , wieso haben wir nun ein Integral über x^2 , wieso haben wir nun ein Integral über x^2 
Edit: Und v.a. - darf der Tensoreintrag bei homog. Dichte wirklich von dieser abhängen?
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 20:57 Titel: dermarkus Verfasst am: 20. Dez 2009 20:57 Titel: |
 |
|
| Airblader hat Folgendes geschrieben: |
Einmal ein Diagonalelement:
~\dd x = 4\varrho)
|
Was du hier ausgerechnet hast, ist das I_yy gewesen.
Was muss deiner unten schon richtig angefangenen Überlegung nach in dem Integral für I_xx drin stehen? |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 20:59 Titel: Airblader Verfasst am: 20. Dez 2009 20:59 Titel: |
 |
|
aaah ... es dämmert.
Klar, da muss y² drinstehen. Und das z² ist ja immer Null, da keine Dicke, right?
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 21:03 Titel: dermarkus Verfasst am: 20. Dez 2009 21:03 Titel: |
 |
|
| Airblader hat Folgendes geschrieben: |
Edit: Und v.a. - darf der Tensoreintrag bei homog. Dichte wirklich von dieser abhängen?
|
Wenn man so eine Aufgabe samt Längeneinheiten rechnet, dann merkt man, dass die Einheit des Ergebnisses nicht die einer Flächendichte, sondern die Einheit einer Flächendichte mal (Längeneinheit hoch vier) ist. Also die Einheit von Masse mal (Länge zum Quadrat), zum Beispiel kg*m^2.
Noch übersichtlicher bzw. verständlicher werden also oft die Endergebnisse, wenn du die Gesamtfläche A des Dreieckes ausrechnest und die Ergebnisse mit Hilfe der Gesamtmasse  ausdrückst. ausdrückst. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 21:04 Titel: dermarkus Verfasst am: 20. Dez 2009 21:04 Titel: |
 |
|
| Airblader hat Folgendes geschrieben: | aaah ... es dämmert.
Klar, da muss y² drinstehen.
|
Einverstanden 
| Zitat: |
Und das z² ist ja immer Null, da keine Dicke, right?
|
Das z^2 ist immer null, weil wegen der als sehr klein angenommenen Dicke alle Punkte des Dreieckes in guter Näherung z=0 haben, einverstanden  |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 21:05 Titel: Airblader Verfasst am: 20. Dez 2009 21:05 Titel: |
 |
|
Ja, ist mir eben auch eingefallen. 
Das habe ich beim Schwerpunkt ja auch schon gemacht. Also ist I_yy einfach gleich 1 (da Flächeninhalt gleich 4 ist).
Super. Dann habe ich alles, um den Tensor zu berechnen. Danke 
Dann käme jetzt Teilaufgabe (b).
Wie muss ich da dann vorgehen? Die Diagonalelemente kann ich mit Steiner verschieben, okay. Muss ich die nicht-Diagonalelemente auch verschieben? Wenn ja, wie?
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 21:14 Titel: dermarkus Verfasst am: 20. Dez 2009 21:14 Titel: |
 |
|
Für die Nicht-Diagonalelemente in b) würde ich einfach vorschlagen, das Koordinatensystem in den Schwerpunkt zu verschieben, die Grenzen der Integrale dementsprechend anzupassen und damit die Integrale neu auszurechnen, das geht bestimmt schon mal.
Für die Diagonalelemente in b) kommt diese Methode sicher auch in Frage, wobei Steiner da einfacher und schneller sein könnte (vielleicht ist er ja auch einfach eine nette Zusatz-Kontrolle  ) ) |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 21:18 Titel: Airblader Verfasst am: 20. Dez 2009 21:18 Titel: |
 |
|
Ah, da habe ich gar nicht mehr dran gedacht.
Okay - ich denke, dass das die Verständnisprobleme der Aufgabe erstmal eliminiert hat. Die Integrale zu berechnen ist dann kein Problem mehr.
Ein supergroßes Dankeschön, an alle, speziell natürlich an dich, dermarkus. 
Jetzt müsste ich noch ein paar andere Sachen verstehen, aber eins nach dem anderen. Morgen kommt erstmal die AnaI-Klausur.
Danke!
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 21:25 Titel: dermarkus Verfasst am: 20. Dez 2009 21:25 Titel: |
 |
|
Eins noch:
| Airblader hat Folgendes geschrieben: | Also ist I_yy einfach gleich 1 (da Flächeninhalt gleich 4 ist).
|
Ich glaube, du meinst da entweder I_yy = M, oder du hast verwendet, dass die Masse des Dreiecks 1 sein soll, stimmts? |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 21:27 Titel: Airblader Verfasst am: 20. Dez 2009 21:27 Titel: |
 |
|
Ja, ich meinte natürlich M. War ein langer Tag! 
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 21:31 Titel: Airblader Verfasst am: 20. Dez 2009 21:31 Titel: |
 |
|
Nur noch als kurzer Check, ich habe jetzt

air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Dez 2009 21:52 Titel: dermarkus Verfasst am: 20. Dez 2009 21:52 Titel: |
 |
|
| Airblader hat Folgendes geschrieben: |

|
Einverstanden 
(Irgendwie eine tolle Belohnung, wenn am Ende so einer Rechnung sowas einfaches rauskommt  Das hat man bei Trägheitsmomentintegralen öfter Das hat man bei Trägheitsmomentintegralen öfter  ) ) |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 20. Dez 2009 22:01 Titel: Airblader Verfasst am: 20. Dez 2009 22:01 Titel: |
 |
|
Habe den zweiten Tensor jetzt auch, sowie dank Matlab die Hauptachsentransformation.
Ist zwar nur ein geringer Teil, aber letztlich ging es mir vor allem darum, das Ganze zu verstehen.
Nochmal ein Riesen-Dankeschön 
Jetzt spring ich aber ins Bett, morgen wartet meine erste Klausur im Studium 
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
Airblader
Anmeldungsdatum: 07.05.2006
Beiträge: 129
Wohnort: Geislingen
|
 Airblader Verfasst am: 21. Dez 2009 15:45 Titel: Airblader Verfasst am: 21. Dez 2009 15:45 Titel: |
 |
|
Hi,
kleines Feedback - ein Fehler war zwar drin, aber nur eine Kleinigkeit beim Berechnen d. Integrals.
Ansonsten hat soweit alles gepasst - supervielen Dank nochmal!
War übrigens der Einzige, der es hatte ... 
air
_________________
"Mehr als die Vergangenheit interessiert mich die Zukunft, denn in ihr gedenke ich zu leben." (Albert Einstein) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Dez 2009 15:53 Titel: dermarkus Verfasst am: 21. Dez 2009 15:53 Titel: |
 |
|
Gratuliere  |
|
 |
|

















 ).
).
