| Autor |
Nachricht |
Dreimal0
Anmeldungsdatum: 20.09.2020
Beiträge: 11
|
 Dreimal0 Verfasst am: 20. Sep 2020 13:56 Titel: Höhe des Sprungturms Dreimal0 Verfasst am: 20. Sep 2020 13:56 Titel: Höhe des Sprungturms |
 |
|
Meine Frage:
Ein Schwimmer lässt sich vom Rand des Sprungturms aus vornüber ins Wasser fallen. Während des ganzen Sprunges hält er sich völlig stocksteif; die Bewegung beginnt mit einem ganz langsamen Vorkippen aus der Vertikalen Richtung. Bei welchem Winkel (gegen die Vertikale) verliert der Springer den Kontakt mit dem Sprungbrett? Wie hoch müsste der Sprungturm sein, wenn der Schwimmer nach genau einer vollen Umdrehung mit den Füßen voran ins Wasser eintauchen soll?
[Schwimmer als 2m langer homogener Stab!]
Meine Ideen:
Bleibt der Drehpunkt, um den der Schimmer rotiert während des gesamten Vorgangs unverändert? Dreht er sich also während des gesamten "Sprungs" immer um seine Füße oder ändert sich die Drehachse?
Vielen Dank im voraus für hilfreiche Tipps, "die zur Ergreifung des Täters beitragen"!
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 20. Sep 2020 16:54 Titel: Myon Verfasst am: 20. Sep 2020 16:54 Titel: |
 |
|
Der Springer dreht sich um seine Füsse auf dem Sprungbrett, bis er den Kontakt mit dem Sprungbrett verliert.
Bei der ersten Teilaufgabe könntest Du folgendermassen vorgehen (Irrtum vorbehalten!):
-aus dem Energieerhaltungssatz folgt die Winkelgeschwindigkeit ) des Springers in Abhängigkeit vom Winkel des Springers in Abhängigkeit vom Winkel  zur Vertikalen. zur Vertikalen.
-der Schwerpunkt des Schwimmers bewegt sich auf einer Kreisbahn, seine Beschleunigung in radialer Richtung ergibt sich mit der üblichen Formel (v^2/r).
-die Gewichtskraft kann in eine radial wirkende Komponente und eine senkrecht dazu zerlegt werden. Bei einem bestimmten Winkel  ist die radiale Beschleunigung höher als die radial wirkende Komponente der Gewichtskraft; das müsste der gesuchte Winkel sein, wo sich der Springer vom Sprungbrett löst (ich erhalte etwa 53 Grad). ist die radiale Beschleunigung höher als die radial wirkende Komponente der Gewichtskraft; das müsste der gesuchte Winkel sein, wo sich der Springer vom Sprungbrett löst (ich erhalte etwa 53 Grad).
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 20. Sep 2020 18:11 Titel: Mathefix Verfasst am: 20. Sep 2020 18:11 Titel: |
 |
|
|
Der Springer kippt, wenn sein Körperschwerpunkt vor der Kippkante (Fussspitzen/Kante Brett) liegt, denn dann ist das Kippmoment > Standmoment.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 20. Sep 2020 21:24 Titel: Myon Verfasst am: 20. Sep 2020 21:24 Titel: |
 |
|
Vielleicht noch kurz ein, zwei Tipps zum 2. Teil, der Frage nach der Höhe des Sprungbretts:
Beim gesuchten Winkel, wo sich der Springer vom Sprungbrett löst, hat er eine bestimmte Winkelgeschwindigkeit. Diese bleibt bis zum Eintauchen ins Wasser konstant. Dadurch ergibt sich die Zeit, die zwischen dem Loslösen vom Sprungbrett und dem Eintauchen vergeht, und mit dieser wiederum die Höhendifferenz (freier Fall nach dem Loslösen; beachte, beim Loslösen hat der Springer bereits eine senkrechte Komponente der Geschwindigkeit).
Für die Höhe des Sprungbretts noch die Höhe des Schwerpunkts beim Eintauchen sowie die Höhe beim Loslösen addieren bzw. subtrahieren.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Sep 2020 11:02 Titel: Mathefix Verfasst am: 21. Sep 2020 11:02 Titel: |
 |
|
@Myon
Ich habe Deine Rechnung nachvollzogen und komme ebenfalls auf den Winkel
 = 53,1°)
Das würde bedeuten, daß bei diesem Winkel der Schwerpunkt eines kippenden dünnen Stabs die Kreisbahn tangential mit der Anfangsgeschwindigkeit
) } = 2,4 m/s )
verlässt. Da es sich bei dem Stab um einen starren Körper handelt, folgt der gesamte Stab dieser Tangentialbewegung, die vom freien Fall und von der Rotation um den Fusspunkt des Stabs überlagert wird.
Über die resultierende Bahnkurve des Schwerpunkts muss ich noch nachdenken.
Zuletzt bearbeitet von Mathefix am 21. Sep 2020 12:27, insgesamt einmal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 21. Sep 2020 12:26 Titel: Myon Verfasst am: 21. Sep 2020 12:26 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | Das würde bedeuten, daß bei diesem Winkel der Schwerpunkt eines kippenden dünnen Stabs die Kreisbahn tangential mit der Anfangsgeschwindigkeit v_0 = 2,4 m/s verlässt. |
Der Schwerpunkt bewegt sich ab diesem Winkel auf einer parabelförmigen Bahn (es wirkt nur noch die Gewichtskraft, vgl. schiefer Wurf), der Krümmungsradius wird grösser als bei einer Kreisbahn bei festem Fussende.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Sep 2020 12:41 Titel: Mathefix Verfasst am: 21. Sep 2020 12:41 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | Das würde bedeuten, daß bei diesem Winkel der Schwerpunkt eines kippenden dünnen Stabs die Kreisbahn tangential mit der Anfangsgeschwindigkeit v_0 = 2,4 m/s verlässt. |
Der Schwerpunkt bewegt sich ab diesem Winkel auf einer parabelförmigen Bahn (es wirkt nur noch die Gewichtskraft, vgl. schiefer Wurf), der Krümmungsradius wird grösser als bei einer Kreisbahn bei festem Fussende. |
Das ist klar. Der Schwerpunkt rotiert gleichzeitig mit dieser Geschwindigkeit um den Fusspunkt des Stabs. Über die daraus resultierende Bahnkurfe muss ich noch nachdenken. Muss irgendwas zykloidisches sein ...
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 21. Sep 2020 12:50 Titel: Myon Verfasst am: 21. Sep 2020 12:50 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | Über die daraus resultierende Bahnkurfe muss ich noch nachdenken. Muss irgendwas zykloidisches sein ... |
Weshalb?
-Vor dem gesuchten Winkel: Springer dreht sich um festes Fussende, der Schwerpunkt bewegt sich auf einer Kreisbahn
-Nach diesem Winkel: der Schwerpunkt bewegt sich auf einer Parabelbahn, gleichzeitig dreht sich der Springer mit konstanter Winkelgeschwindigkeit um seinen Schwerpunkt.
|
|
 |
Zerdenker
Anmeldungsdatum: 05.08.2020
Beiträge: 77
|
 Zerdenker Verfasst am: 21. Sep 2020 13:47 Titel: Zerdenker Verfasst am: 21. Sep 2020 13:47 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | @Myon
Da es sich bei dem Stab um einen starren Körper handelt, folgt der gesamte Stab dieser Tangentialbewegung, die vom freien Fall und von der Rotation um den Fusspunkt des Stabs überlagert wird.
|
Verstehe ich nicht, solange der Kontakt zum Sprungturm da ist würde ich zustimmen, dann ist es eine Rotation um den Fußpunkt. Aber sobald kein Bodenkontakt mehr da ist und der Springer im freien Fall ist, müsste die Rotation doch um seinen Schwerpunkt stattfinden oder nicht?
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 21. Sep 2020 14:21 Titel: Nils Hoppenstedt Verfasst am: 21. Sep 2020 14:21 Titel: |
 |
|
Hallo,
ich stelle hiermit meine Lösung ebenfalls zur Diskussion.
Ausgangspunkt ist das 2. Newtonsche Axiom für Starrkörperrotationen:

Das Drehmoment ist gegeben durch die am Schwerpunkt angreifende Gewichtskraft:
 )
wobei  der Winkel des Springers gegenüber der Horizontalen ist. Es gilt also: der Winkel des Springers gegenüber der Horizontalen ist. Es gilt also:
 = I\dot{\omega} \quad (*) )
Der Schwerpunkt kann in senkrechter Richtung nur mit maximal g beschleunigen, es gilt also:
 \le g )
Eliminiert man in dieser Gleichung 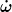 mit Hilfe von Gleichung (*) und ersetzt noch das Träheitsmoment für einen homogenen Stab I = 1/3ml², so folgt mit Hilfe von Gleichung (*) und ersetzt noch das Träheitsmoment für einen homogenen Stab I = 1/3ml², so folgt
 \le \sqrt{3/4} = 58.4°)
... was nahe an der Lösung von Myon ist.
Viele Grüße,
Nils
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 21. Sep 2020 15:25 Titel: Myon Verfasst am: 21. Sep 2020 15:25 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: |  \le \sqrt{3/4} = 58.4°) |
Diese Ungleichung hat mich etwas ins Stutzen gebracht, da ich mich gefragt habe, was das für den Fall bedeuten würde, wo der Springer um eine beim Fussende fixierte Achse rotieren würde. Wenn ich nachrechne, komme ich allerdings auf
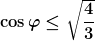
Was zum Glück für jeden Winkel erfüllt ist. Beim Winkel phi=53° handelt es sich übrigens um den Winkel zur Vertikalen.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 21. Sep 2020 15:33 Titel: Nils Hoppenstedt Verfasst am: 21. Sep 2020 15:33 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Was zum Glück für jeden Winkel erfüllt ist. Beim Winkel phi=53° handelt es sich übrigens um den Winkel zur Vertikalen. |
Bei mir ist phi der Winkel zur Horizontalen (ich hab das noch nachträglich oben erwähnt).
Viele Grüße,
Nils
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Sep 2020 17:17 Titel: Mathefix Verfasst am: 21. Sep 2020 17:17 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Nils Hoppenstedt hat Folgendes geschrieben: |  \le \sqrt{3/4} = 58.4°) |
Diese Ungleichung hat mich etwas ins Stutzen gebracht, da ich mich gefragt habe, was das für den Fall bedeuten würde, wo der Springer um eine beim Fussende fixierte Achse rotieren würde. Wenn ich nachrechne, komme ich allerdings auf
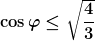
. |
cos phi > 1 ?
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Sep 2020 17:27 Titel: Mathefix Verfasst am: 21. Sep 2020 17:27 Titel: |
 |
|
Hallo Nils,
Ich interpretiere Dein Ergebnis so, dass bei dem Winkel die vertikale Beschleunigung g erreicht ist. Das ist nicht der Winkel bei dem der Schwerpunkt abhebt.
Gruss
mathefix
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 21. Sep 2020 17:48 Titel: Nils Hoppenstedt Verfasst am: 21. Sep 2020 17:48 Titel: |
 |
|
Mir ist nicht ganz klar, was du mit "abheben" meinst.
Mein Ansatz ist folgender: Solange Kontakt besteht, kann man die Bewegung als Kippfall um den Fußpunkt beschreiben (mit den angegebenen Bewegungsgleichungen). Daraus resultiert eine vertikale Beschleunigung des Schwerpunkts. Da der Schwerpunkt aber nicht mit einer höheren Beschleunigung fallen kann als g (der Körper kann ja schneller fallen als im freien Fall), muss bei dem angegebenen Winkel der Kontakt abreißen.
Viele Grüße,
Nils
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Sep 2020 17:54 Titel: Mathefix Verfasst am: 21. Sep 2020 17:54 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | Mir ist nicht ganz klar, was du mit "abheben" meinst.
|
Mit "abheben" meinte ich das tangentiale Verlassen der Kreisbahn des Schwerpunkts mit Übergang in die parabolische Flugbahn.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 21. Sep 2020 17:57 Titel: Nils Hoppenstedt Verfasst am: 21. Sep 2020 17:57 Titel: |
 |
|
|
Ah ok, ich glaube, dann reden wir über das selbe....
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Sep 2020 18:02 Titel: Mathefix Verfasst am: 21. Sep 2020 18:02 Titel: |
 |
|
[quote="Nils Hoppenstedt"]
Mein Ansatz ist folgender: Solange Kontakt beste...Da der Schwerpunkt aber nicht mit einer höheren Beschleunigung fallen kann als g (der Körper kann ja schneller fallen als im freien Fall), muss bei dem angegebenen Winkel der Kontakt abreißen.
Viele Grüße,
Nils
[quote]
Auf den Schwerpunkt wirkt auch eine horizontale Beschleunigungskomponente.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Sep 2020 18:21 Titel: Mathefix Verfasst am: 21. Sep 2020 18:21 Titel: |
 |
|
[quote="Nils Hoppenstedt"]Ja und?[/quote
Ich meine, dass die berücksichtigt werden muss, denn es ist nicht gefragt wann der Schwerpunkt die Kreisbahn nur vertikal verlässt. Die Berücksichtigung der Horizontalbeschleunigung ergibt einen kleineren Winkel- das Abheben tritt eher ein.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 21. Sep 2020 18:22 Titel: Myon Verfasst am: 21. Sep 2020 18:22 Titel: |
 |
|
@Nils Hoppenstedt: Wie gesagt, ich glaube, dass der Ungleichung
| Nils Hoppenstedt hat Folgendes geschrieben: |  \le \sqrt{3/4}) |
ein kleiner Umformungsfehler zugrundeliegt (oder hab ich mich vertan?). Der Schwerpunkt kann jedenfalls in der Tat maximal mit g beschleunigt werden, und das gilt für jeden Winkel. Der Springer/Stab könnte ja auch um eine fixierte Achse rotieren, und dann gibt es keinen „kritischen“ Winkel.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 21. Sep 2020 18:34 Titel: Myon Verfasst am: 21. Sep 2020 18:34 Titel: |
 |
|
@Mathefix: Natürlich hat der Schwerpunkt auch eine horizontale Beschleunigungskomponente, die durch die Kraft vom Sprungbrett auf den Fuss bewirkt wird (allerdings nur bis zum kritischen Winkel). Diese Komponente spielt m.E. aber für die Berechnung keine Rolle.
Relevant ist, dass der Schwerpunkt auf einer Kreisbahn gehalten werden kann, und dazu ist eine Zentripetalkraft von mindestens m*v^2/r nötig. Diese Zentripetalkraft kann nur von der radialen Komponente der Gewichtskraft herrühren. Ab einem gewissen Winkel reicht diese Komponente nicht mehr aus, und der Schwerpunkt verlässt die Kreisbahn - der Abstand zum Sprungbrett wird grösser als l/2.
Zuletzt bearbeitet von Myon am 21. Sep 2020 18:37, insgesamt einmal bearbeitet |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 21. Sep 2020 18:37 Titel: Nils Hoppenstedt Verfasst am: 21. Sep 2020 18:37 Titel: |
 |
|
| Myon hat Folgendes geschrieben: |
| Nils Hoppenstedt hat Folgendes geschrieben: |  \le \sqrt{3/4}) |
ein kleiner Umformungsfehler zugrundeliegt (oder hab ich mich vertan?). |
Ja, stimmt. Mist!
An deinem Ansatz stört mich ein bisschen, dass das Trägheitsmoment überhaupt nicht eingeht oder hab ich da was übersehen?
Viele Grüße,
Nils
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 21. Sep 2020 18:42 Titel: Myon Verfasst am: 21. Sep 2020 18:42 Titel: |
 |
|
Doch, das Trägheitsmoment geht in die Gleichung für ) ein. (Aus Energieerhaltung ein. (Aus Energieerhaltung
=\frac{1}{2}I\omega^2) ) )
100% sicher bin ich ja auch nicht, dass die Überlegung und Rechnung stimmt, von dem her bin ich gerne an anderen Lösungen interessiert.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Sep 2020 19:25 Titel: Mathefix Verfasst am: 21. Sep 2020 19:25 Titel: |
 |
|
Mich irritiert, dass sich nach den bisherigen Berechnungen der Fusspunkt des Stabs nach Überschreiten des kritischen Winkels vom Drehpunkt wegbewegen müsste, da der Schwerpunkt des Stabs die Kreisbahn verlässt. Das ist nicht zu beobachten. Der mir bekannte Ansatz zum fallenden Stab geht davon aus, dass der Fusspunkt im Drehpunkt verbleibt, solange der Fusspunkt eine Kraft auf die Kontaktfläche ausübt.
Danach würde der Fusspunkt die Kante des Sprungbretts bei einem Winkel von 0° zur Horizontalen verlassen.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 21. Sep 2020 20:35 Titel: Nils Hoppenstedt Verfasst am: 21. Sep 2020 20:35 Titel: |
 |
|
| Myon hat Folgendes geschrieben: |
100% sicher bin ich ja auch nicht, dass die Überlegung und Rechnung stimmt, von dem her bin ich gerne an anderen Lösungen interessiert. |
Hallo Myon,
ich hab mir deine Lösung nochmal durch den Kopf gehen lassen und denke jetzt auch, dass sie richtig ist. Danke fürs Posten! 
Ich war zuerst von dem hier irritiert:
| Zitat: | | der Schwerpunkt des Schwimmers bewegt sich auf einer Kreisbahn, seine Beschleunigung in radialer Richtung ergibt sich mit der üblichen Formel (v^2/r). |
da es sich zuerst so anhört, als würdest du den Körper durch seinen Schwerpunkt ersetzen und so den Einfluss der unterschiedlichen Abstände der Massepunkte vom Drehpunkt ignorieren.
Allgemein müsste man nämlich die notwendige Zentripetalkraft für jedes Masseelement, das sich im Abstand r vom Drehpunkt befindet, ausrechnen und dann über alle Massepunkte integrieren:
 \omega^2 r)
Nun ist aber beim homogenen Stab die Massendichte 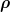 konstant und es folgt: konstant und es folgt:

Für einen homogenen Stab ist die notwendige Gesamt-Zentripetalkraft also die gleiche, die sich ergibt, wenn die gesamte Masse am Schwerpunkt konzertiert wäre. Dein Ansatz ist also richtig!
(Für den allgemeinen Fall einer beliebigen Massenverteilung müsste man aber das Integral ausrechnen.)
| Mathefix hat Folgendes geschrieben: |
Der mir bekannte Ansatz zum fallenden Stab geht davon aus, dass der Fusspunkt im Drehpunkt verbleibt, solange der Fusspunkt eine Kraft auf die Kontaktfläche ausübt.
|
Aber für eine Drehbewegung muss doch stets nach innen eine Zentripetalkraft gerichtet sein, die den Körper auf der Kreisbahn hält. In unserem Fall kann diese aber höchstens so groß sein wie die radiale Komponente der Gewichtskraft. Beim obigen Grenzwinkel ist dies aber nicht mehr der Fall; die Kreisbewegung ist also nicht mehr möglich.
Viele Grüße,
Nils
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 21. Sep 2020 21:04 Titel: Myon Verfasst am: 21. Sep 2020 21:04 Titel: |
 |
|
Genau, hatte mir bez. den einzelnen Massenpunkten im Stab/Springer auch etwas den Kopf zerbrochen! Im Stab muss es zu Zug-/Druckspannungen kommen.
Anderseits muss man m.E. hier nicht nachrechnen. Unabhängig von der Form des Körpers beträgt die Beschleunigung eines Punktes auf einer Kreisbahn v^2/r, dies ergibt sich alleine aus der Bahnkurve des Punktes und gilt auch für den Schwerpunkt. Folglich muss über den Stab integriert die Kraft m*v^2/r auf den Stab wirken, denn gemäss dieser Kraftsumme wird der Schwerpunkt beschleunigt (Schwerpunktsatz). Bei inhomogener Dichte muss einfach berücksichtigt werden, dass die Gewichtskraft am Schwerpunkt angreift, der dann nicht mehr in der Mitte liegt.
| Mathefix hat Folgendes geschrieben: | | Mich irritiert, dass sich nach den bisherigen Berechnungen der Fusspunkt des Stabs nach Überschreiten des kritischen Winkels vom Drehpunkt wegbewegen müsste, da der Schwerpunkt des Stabs die Kreisbahn verlässt. Das ist nicht zu beobachten. |
Weshalb, was ist denn zu beobachten? Ich kann das nicht gut überprüfen, doch ein Stab, der auf einer Unterlage fallen gelassen wird und bei dem ein Gleiten auf der Unterlage gegen eine Seite verhindert wird (analog dem Sprungbrett), müsste ab einem bestimmten Winkel auf der Unterlage „nach vorne“ wegrutschen.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 21. Sep 2020 22:16 Titel: VeryApe Verfasst am: 21. Sep 2020 22:16 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | -die Gewichtskraft kann in eine radial wirkende Komponente und eine senkrecht dazu zerlegt werden. Bei einem bestimmten Winkel  ist die radiale Beschleunigung höher als die radial wirkende Komponente der Gewichtskraft; das müsste der gesuchte Winkel sein, wo sich der Springer vom Sprungbrett löst (ich erhalte etwa 53 Grad). ist die radiale Beschleunigung höher als die radial wirkende Komponente der Gewichtskraft; das müsste der gesuchte Winkel sein, wo sich der Springer vom Sprungbrett löst (ich erhalte etwa 53 Grad). |
Dann würde aber bei diesem Winkel im Auflagepunkt ebenfalls die gleiche tangential Beschleunigung wirken, wie im Schwerpunkt, weil nichts mehr übrig wäre was noch die winkelbeschleunigung erhöhen könnte also es wäre FR und FN=0.
Würde sich das nicht widersprechen? im Auflagepunkt ein Anteil nach unten? und FN=0?
Ich hätte jetzt vermutet es gibt einen Punkt bei dem FR=0 ist, vorher drückt es nach aussen aber FN drückt hier noch ein wenig nach oben, dann beginnt FR nach innen zu ziehen aber durch das geringe FN fliegt es irgendwann vorher aus der Haftreibung und ganze rutscht nach aussen.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 21. Sep 2020 22:32 Titel: Nils Hoppenstedt Verfasst am: 21. Sep 2020 22:32 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Folglich muss über den Stab integriert die Kraft m*v^2/r auf den Stab wirken, denn gemäss dieser Kraftsumme wird der Schwerpunkt beschleunigt (Schwerpunktsatz).
|
Ja, richtig. Denn obiges Integral enthält ja bereits die Formel für den Schwerpunkt:
 \omega^2 r = m\omega² s_r)
Viele Grüße,
Nils
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 22. Sep 2020 08:25 Titel: Mathefix Verfasst am: 22. Sep 2020 08:25 Titel: |
 |
|
Ansatz von Nils:
 Winkel zur Horizontalen Winkel zur Horizontalen
 = I\cdot \dot{\omega } )
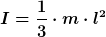

= \frac{3}{4} \cdot g )
Eine vertkale Beschleunigung g des Massenschwerpunktes wird bei keinem Winkel erreicht.
Reibung
Ein am Fusspunkt reibungsfrei frei aufliegender Stab wird bei Neigung sofort weggleiten. Ohne Reibung keine Rotation.
Mit den Gleichungen von VeryApe zu den Kräften am Fusspunkt kann bei gegebenem Reibwert ermittel werden, bis zu welchem Winkel der Fusspunkt nicht gleitet bzw. wie gross der Reibwert sein muss, damit der Stab bis zum kritischen Winkel rotiert.
Oder man geht, wie in dem mir bekannten Ansatz von einem reibungsfrei gelagerten Stab aus. Dessen Schwerpunkt verlässt die Kreisbahn nicht.
Zuletzt bearbeitet von Mathefix am 22. Sep 2020 09:58, insgesamt einmal bearbeitet |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 22. Sep 2020 08:47 Titel: VeryApe Verfasst am: 22. Sep 2020 08:47 Titel: |
 |
|
| mathefix hat Folgendes geschrieben: |
Ein am Fusspunkt reibungsfrei frei aufliegender Stab wird bei Neigung sofort weggleiten. Ohne Reibung keine Rotation.
|
Bei einem reibungsfrei gelagerten Stab, würde der Schwerpunkt auf einer vertikalen Geraden nach unten fallen. Rotation gibts trotzdem weil FN um den Schwerpunkt dreht. Der Auflagepunkt kann ja nicht in den Boden hineinwandern, daher wird der Auflagepunkt am Boden gleiten, so dass der Schwerpunkt gerade heruntenfallen kann, Ohne FR keine horizontale Beschleunigung.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 22. Sep 2020 08:53 Titel: Myon Verfasst am: 22. Sep 2020 08:53 Titel: |
 |
|
@Mathefix: Für den von Dir erwähnten Fall ohne Reibung siehe die Erklärung von VeryApe. Den Fall, den Du vermutlich meinst - einfach ein kippender Stab auf einer Unterlage - setzt eine genügend grosse Haftreibung voraus. Der Stab rotiert dann um sein Fussende, welches ortsfest bleibt. Der Stab bricht auch nicht nach vorne aus, wie im vorliegenden Fall (sofern die Lösung richtig ist).
PS: OK, Du schreibst ja selber, ohne Reibung keine Rotation. Im vorliegenden Fall gibt es unbeschränkt hohe Haftreibung - allerdings nur in eine Richtung.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 22. Sep 2020 09:05 Titel: Myon Verfasst am: 22. Sep 2020 09:05 Titel: |
 |
|
Hier noch die gewünschte ausführliche Herleitung, wie man auf den Winkel von 53.1° kommt.
Energieerhaltung: Die Summe aus potentieller und kinetischer Energie (hier: Rotationsenergie) muss zeitlich konstant und daher für jeden Winkel  gleich sein: gleich sein:
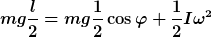
Rechts ist die Energie ganz zu Beginn bei 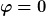 , rechts die Energie bei beliebigem Winkel , rechts die Energie bei beliebigem Winkel  ( ( ist die Höhendifferenz zwischen Schwerpunkt und Sprungbrett). Dies gilt, solange der Springer Kontakt mit dem Sprungbrett hat. Der letzte Term ist die Rotationsenergie, I ist das Massenträgheitsmoment eines dünnen Stabes bei Rotation um ein Stabende. Es gilt ist die Höhendifferenz zwischen Schwerpunkt und Sprungbrett). Dies gilt, solange der Springer Kontakt mit dem Sprungbrett hat. Der letzte Term ist die Rotationsenergie, I ist das Massenträgheitsmoment eines dünnen Stabes bei Rotation um ein Stabende. Es gilt 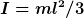 und somit und somit
=\frac{1}{6}ml^2\omega^2)
=\sqrt{\frac{3g}{l}(1-\cos\varphi)})
Bewegt sich ein Punkt auf einer Kreisbahn mit Radius r, beträgt seine Beschleunigung in radialer Richtung  . Die radiale Komponenente der Beschleunigung des Schwerpunkts (Komponente parallel zum Stab) ist also . Die radiale Komponenente der Beschleunigung des Schwerpunkts (Komponente parallel zum Stab) ist also
)
Solange der Schwerpunkt auf einer Kreisbahn mit Radius l/2 bleibt, muss eine entsprechend hohe Zentripetalkraft 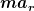 wirken. Dies kann hier nur von der Gewichtskraft herrühren, deren radiale Komponente ist wirken. Dies kann hier nur von der Gewichtskraft herrühren, deren radiale Komponente ist
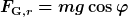
Beim gesuchten kritischen Winkel gilt 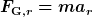 und damit und damit
)
Bei grösserem Winkel  wird wird 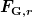 kleiner als die notwendige Zentripetalkraft. Der Krümmungsradius der Bahn des Schwerpunkts nimmt zu, und sein Abstand zum Sprungbrett wird grösser als l/2. Der Stab/Schwimmer verliert den Kontakt zum Sprungbrett. kleiner als die notwendige Zentripetalkraft. Der Krümmungsradius der Bahn des Schwerpunkts nimmt zu, und sein Abstand zum Sprungbrett wird grösser als l/2. Der Stab/Schwimmer verliert den Kontakt zum Sprungbrett.
Zuletzt bearbeitet von Myon am 22. Sep 2020 09:23, insgesamt einmal bearbeitet |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 22. Sep 2020 09:19 Titel: VeryApe Verfasst am: 22. Sep 2020 09:19 Titel: |
 |
|
hm du gehst davon aus, daß die meinen die Haftreibung wäre unbeschränkt , aber FR nur nach aussen wirken kann?
Dann wäre das doch der Fall, wenn FR null wird in der Gleichung, die ich für FR hingeschrieben habe. Dann würde es nach dieser Vorstellung nach aussen zu rutschen beginnen, in Wirklichkeit fängt FR da erst nach innen zu ziehen an.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 22. Sep 2020 09:27 Titel: Mathefix Verfasst am: 22. Sep 2020 09:27 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | mathefix hat Folgendes geschrieben: |
Ein am Fusspunkt reibungsfrei frei aufliegender Stab wird bei Neigung sofort weggleiten. Ohne Reibung keine Rotation.
|
Bei einem reibungsfrei gelagerten Stab, würde der Schwerpunkt auf einer vertikalen Geraden nach unten fallen. Rotation gibts trotzdem weil FN um den Schwerpunkt dreht. Der Auflagepunkt kann ja nicht in den Boden hineinwandern, daher wird der Auflagepunkt am Boden gleiten, so dass der Schwerpunkt gerade heruntenfallen kann, Ohne FR keine horizontale Beschleunigung. |
@VeryApe
Da habe ich mich unklar ausgedrückt. Mit Rotaton meinte ich Rotation um den Fusspunkt. Der Stab rotiert bei Weggleiten um seinen Schwerpunkt.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 22. Sep 2020 09:29 Titel: Myon Verfasst am: 22. Sep 2020 09:29 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: | -die Gewichtskraft kann in eine radial wirkende Komponente und eine senkrecht dazu zerlegt werden. Bei einem bestimmten Winkel  ist die radiale Beschleunigung höher als die radial wirkende Komponente der Gewichtskraft; das müsste der gesuchte Winkel sein, wo sich der Springer vom Sprungbrett löst (ich erhalte etwa 53 Grad). ist die radiale Beschleunigung höher als die radial wirkende Komponente der Gewichtskraft; das müsste der gesuchte Winkel sein, wo sich der Springer vom Sprungbrett löst (ich erhalte etwa 53 Grad). |
Dann würde aber bei diesem Winkel im Auflagepunkt ebenfalls die gleiche tangential Beschleunigung wirken, wie im Schwerpunkt, weil nichts mehr übrig wäre was noch die winkelbeschleunigung erhöhen könnte also es wäre FR und FN=0. |
Beim kritischen Winkel werden die radiale Komponente der Gewichtskraft und die notwendige Zentripetalkraft gleich. Dann wirkt vom Sprungbrett auch keine Kraft mehr in radialer Richtung auf den Springer.
Es kann aber sehr wohl eine Kraft vom Sprungbrett senkrecht zum Springer wirken. Die Normalkraft kann ja auch nicht =0 sein, da sonst der Schwerpunkt mit g beschleunigt würde.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 22. Sep 2020 09:39 Titel: VeryApe Verfasst am: 22. Sep 2020 09:39 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Es kann aber sehr wohl eine Kraft vom Sprungbrett senkrecht zum Springer wirken. Die Normalkraft kann ja auch nicht =0 sein, da sonst der Schwerpunkt mit g beschleunigt würde.
|
Denk dich mal kurz in den Schwerpunkt, wenn FN!=0 dann bildet ein vertiakler Teil der Gewichtskraft im Schwerpunkt mit FN ein reines Drehmoment, daß den Schwerpunkt nicht beschleunigt, sondern nur rein um den Schwerpunkt dreht, dann bleibt ein anderer vertikalr Teil über nämlich G-FN, denn du dann in in eine tangentiale und radiale Beschleunigung zerlegen kannsd, der auch wirklich den Schwerpunkt beschleunigt.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 22. Sep 2020 09:46 Titel: Mathefix Verfasst am: 22. Sep 2020 09:46 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | Ich komme da auf folgende Gleichungen für FR und FN:

 |
Gleichgewichtsbedingung mit Reibung: Fusspunkt ist ortsfest bis zum kritischen Winkel


Reibwert, der mindestens notwenig ist, um den kritischen Winkel zu erreichen:
 }{F_N(\varphi_k)} )
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 22. Sep 2020 10:33 Titel: Myon Verfasst am: 22. Sep 2020 10:33 Titel: |
 |
|
@VeryApe: Deinen obigen Beitrag über den Schwerpunkt konnte ich noch nicht recht verstehen. Aber ich sehe nun schon das Problem. Zum einen: was ich oben geschrieben habe, dass die Haftreibungskraft nur in eine Richtung wirken würde, ist falsch. Die Haftreibungskraft wirkt zuerst nach vorne, ab einem bestimmten Winkel dann aber nach „hinten“ - der Schwerpunkt wird offenbar horizontal wieder Richtung Sprungbrett beschleunigt.
Ich denke, was bei einem Stab auf einer Unterlage nach dem kritischen Winkel passiert, ist tatsächlich nicht ganz einfach zu verstehen. Das Fussende des Stabes muss auf der Unterlage bleiben, doch die Normalkraft ist =0 (man kann sich infinitesimal kleine Bewegungen vorstellen abwechslungsweise in radialer Richtung nach aussen, dann wieder senkrecht dazu nach schräg unten im freien Fall). Der Stab rutscht also nach vorne.
Beim Sprungbrett ist das nicht möglich. Hat sich der Springer einmal nur ganz kurz vom Sprungbrett in radialer Richtung gelöst, befindet er sich vor dem Sprungbrett und im freien Fall.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 22. Sep 2020 11:24 Titel: Nils Hoppenstedt Verfasst am: 22. Sep 2020 11:24 Titel: |
 |
|
| Myon hat Folgendes geschrieben: |
Ich denke, was bei einem Stab auf einer Unterlage nach dem kritischen Winkel passiert, ist tatsächlich nicht ganz einfach zu verstehen. Das Fussende des Stabes muss auf der Unterlage bleiben, doch die Normalkraft ist =0 (man kann sich infinitesimal kleine Bewegungen vorstellen abwechslungsweise in radialer Richtung nach aussen, dann wieder senkrecht dazu nach schräg unten im freien Fall). Der Stab rutscht also nach vorne.
|
Ja, die genaue Dynamik unmittelbar nach Erreichen des kritischen Winkels scheint wirklich kompliziert zu sein: sobald der Stab den Kontakt verliert und in den freien Fall übergeht, drückt das untere Ende wieder auf den Untergrund. Während des Wegrutschens nach vorne wirkt also wieder eine Normalkraft nach oben und bewirkt so ein Drehmoment. Dadurch dreht sich der Stab etwas schneller, was zur Folge hat, dass die Normalkraft wieder abnimmt.... uff.
Viele Grüße,
Nils
|
|
 |
|