| Autor |
Nachricht |
gustav
Gast
|
 gustav Verfasst am: 01. März 2006 20:12 Titel: variables C: Zeitdehnung klassisch ausrechnen gustav Verfasst am: 01. März 2006 20:12 Titel: variables C: Zeitdehnung klassisch ausrechnen |
 |
|
Ich bin vor kurzem auf die Idee gekommen, bei der Herleitung zu der Formel für die Zeitdehnung: t'=Wurzel(1-(v/c)^2)*t,
also von dieser bewegten Lichtuhr und den beiden Beobachtern, bei dem einer sich relativ zu der Lichtuhr in Ruhe befindet, der andere aber sich relativ zu ihr bewegt,
von KLASSISCHEN Gegebenheiten auszugehen, also ein variables C ( c+v, mit v = Geschw. der Lichtuhr ) anzunehmen.
Wenn ich dies tue, müsste ich doch bei der Herleitung zu der obengenannten Formel doch auf t'=t kommen.
Leider konnte ich auch nach langem Herumrechnen nicht zu diesem Ergebnis kommen :-(
Ich bitte deshalb inständig um Hilfe. |
|
 |
Gast
|
 Gast Verfasst am: 01. März 2006 20:25 Titel: Gast Verfasst am: 01. März 2006 20:25 Titel: |
 |
|
Wenn du von klassischen Gegebenheiten ausgeht, sagst du dass (v/c)^2<<1 ist.
Und damit folgt dann t'=t |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 02. März 2006 01:12 Titel: dermarkus Verfasst am: 02. März 2006 01:12 Titel: |
 |
|
Was hast du denn raus für das Verhältnis t'/t ?
Ich denke, auch wenn du klassisch mit einer klassischen Geschwindigkeitsaddition rechnest, bekommst du einen anderen Wert für die Zeitdauer, die ein Lichtstrahl in der Lichtuhr vom einen Spiegel zum anderen und wieder zurück benötigt, als für eine ruhende Uhr.
----
//edit: Ein klassicher Beobachter wird dies allerdings in der Tat nicht als Zeitdauerunterschied, sondern als Unterschied in der Lichtgeschwindigkeit interpretieren.
----
Ich nehme an, du hast mit einer Lichtuhr gerechnet, bei der die Spiegel senkrecht zur Bewegungsrichtung der Lichtuhr stehen, das Licht also immer parallel bzw. antiparallel zur Bewegungsrichtung der Lichtuhr läuft (also klassich gesehen auf dem Hinweg die Geschwindigkeit c+v, und auf dem Rückweg die Geschwindigkeit c-v hat.)
-------------
Ich denke, Gast hat dich nicht ganz richtig verstanden, mit klassisch meintest du wohl nicht, dass du Näherungsrechnungen machen möchtest.
Zuletzt bearbeitet von dermarkus am 02. März 2006 12:42, insgesamt einmal bearbeitet |
|
 |
Gast
|
 Gast Verfasst am: 02. März 2006 01:56 Titel: Gast Verfasst am: 02. März 2006 01:56 Titel: |
 |
|
Nur ist doch die gesamte klassische Physik eine Näherung der Relativistischen.
Davon abgesehen bin ich nicht sicher ob man aus der Formel für die Zeitdilatation (welche ja aus der Lorentztransformation folgt), einfach durch einsetzen eines "variablen c" wieder die klassische Rechnung rausbekommen kann.
Denn diese Formel rührt doch gerade daher, dass die klass. Geschwindigkeitsaddition nicht richtig ist. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 02. März 2006 12:38 Titel: dermarkus Verfasst am: 02. März 2006 12:38 Titel: |
 |
|
Ich gebe Gast recht, dass du nicht das klassische Ergebnis t=t' erhalten wirst, wenn du eine Lichtgeschwindigkeit von c+v ansetzt.
Das Verhältnis der Lichtgeschwindigkeiten im ruhenden und bewegten System kommt vielmehr als Ergebnis heraus, wenn man das auf klassische Weise durchrechnet.
Die interessante Frage lautet hier also: Welche Lichtgeschwindigkeit misst (berechnet) ein klassisch rechnenden Beobachter mit einer Lichtuhr, die sich mit Geschwindigkeit v bewegt?
Die zwei Spiegel der Lichtuhr haben den Abstand d.
------------------------------------
Klassische Rechnung bedeutet folgende Annahmen:
1.) Geschwindigkeiten addieren sich nichtrelativistisch (also nach der Galilei-Transformation)
2.) t=t' , das heißt, bewegte Uhren gehen genauso schnell wie ruhende, es gebe keine Zeitdilatation.
3.) d=d', das heißt, Abstände im bewegten und im ruhenden System seien gleich, es gebe keine Längenkontraktion.
------------------------------------------
1.Fall: Das Licht in der Lichtuhr bewegt sich parallel (und antiparallel) zur Bewegungsrichtung der Uhr. (Die Spiegel der Uhr stehen also senkrecht zur Bewegungsrichtung der Uhr.) Das Licht habe in diesem bewegten Bezugssystem die Lichtgeschwindigkeit c'
Für den Hinweg vom einen Spiegel zum anderen (in Bewegungsrichtung der Uhr) braucht der Lichtstrahl die Zeit t'_{hin}

also ist :
 = d )
also

Für den Rückweg braucht er die Zeit

also

Die Summe dieser Zeiten ist die Zeit t' für Hin- und Rückweg
d+(c'-v)d}{c'^2-v^2}=\frac{2dc'}{c'^2-v^2} =\frac{2d/c'}{1-v^2/c'^2})
Bei einer ruhenden Uhr (also im ruhenden Bezugssystem, in dem die Lichtgeschwindigkeit = c ist) ist die Zeit t für Hin- und Rückweg
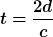
Das Verhältnis zwischen diesen beiden Zeiten ist nach der klassischen Annahme = 1:

Also gilt nach dieser klassischen Betrachtung für das Verhältnis der Lichtgeschwindigkeiten im ruhenden und bewegten System:

----------------------
2. Fall: Die Spiegel der Lichtuhr stehen parallel zur Bewegungsrichtung der Uhr, die Uhr ist also gegenüber Fall 1 um 90° gedreht.
Dieser Fall ist derselbe wie die Betrachtung der Lichtuhr zur Herleitung der Zeitdilatation (daher gebe ich hier nur das Ergebnis an), nur dass der klassische Beobachter das Ergebnis als Unterschied in der Lichtgeschwindigkeit interpretiert:

Wie man sieht, erhält der klassische Beobachter im bewegten System je nach Richtung der Lichtausbreitung unterschiedliche Lichtgeschwindigkeiten. Genau diesen Geschwindigkeitsunterschied versuchte man im Michelson-Morley-Experiment nachzuweisen. (Man maß keinen Unterschied, obwohl die Messgenauigkeit besser als der hier berechnete Unterschied war, wenn man für v die Erdbahngeschwindigkeit einsetzt, und das war ein wichtiges experimentelles Argument dafür, dass eine neue Theorie erforderlich ist.)
Zuletzt bearbeitet von dermarkus am 16. März 2006 23:43, insgesamt einmal bearbeitet |
|
 |
gustav
Gast
|
 gustav Verfasst am: 11. März 2006 20:41 Titel: gustav Verfasst am: 11. März 2006 20:41 Titel: |
 |
|
...dann ist c' aber ( klassisch gesehen ) nicht mehr c+v, sondern es gilt
c' = 1/Wurzel(1-(v/c)^2)* c
oder gilt auch c'=c+v ????
...bin etwas verwirrt, wie ihr seht. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 13. März 2006 16:25 Titel: dermarkus Verfasst am: 13. März 2006 16:25 Titel: |
 |
|
Stimmt. Der Ausdruck für die Differenz der Lichtgeschwindigkeit, den die klassisch betrachtete Lichtuhr misst, ist komplizierter als dein c'=c+v. Denn in der Lichtuhr fliegt das Licht ja sowohl hin als auch her:
In der Herleitung oben für 1.) steckt für den Hinweg des Lichtes die Überlegung "Geschwindigkeit = c' - v", und für den Rückweg des Lichtes die Überlegung "Geschwindigkeit = c' + v". Also misst (siehe Herleitungen oben) der klassische Beobachter mit seiner Lichtuhr etwas komplizierteres als dein c'=c+v.
-------------------------------------------------
Dein c'=c+v gilt also in der klassischen Betrachtung tatsächlich, aber nur auf einer Teilstrecke des Lichtes in der Lichtuhr. Die Lichtgeschwindigkeit, die die Lichtuhr insgesamt misst, ist aber eine andere, nämlich je nach Orientierung der Uhr zur Bewegungsrichtung gilt etwas zwischen den oben hergeleiteten Ergebnissen

und

Zuletzt bearbeitet von dermarkus am 16. März 2006 23:46, insgesamt einmal bearbeitet |
|
 |
gustav
Gast
|
 gustav Verfasst am: 14. März 2006 20:40 Titel: gustav Verfasst am: 14. März 2006 20:40 Titel: |
 |
|
Aber in der Herleitung oben für 2.) müsste doch c'=c+v gelten und nicht
c' = 1/Wurzel(1-(v/c)^2)* c
...sorry euch noch mal zu nerven, Leute |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 14. März 2006 20:58 Titel: dermarkus Verfasst am: 14. März 2006 20:58 Titel: |
 |
|
Wenn du oben in der Herleitung für den 1. Fall die fünfte Formel von oben anschaust, dann siehst du, dass hier tatsächlich die klassisch addierte Geschwindigkeit (c'+v) vorkommt:

Das ist aber nur die klassisch beobachtete Lichtgeschwindigkeit für den Rückweg.
Auf dem Hinweg hat das Licht klassisch die Geschwindigkeit (c'-v).
Und die "effektive" "Gesamt"- Lichtgeschwindigkeit, die für den gesamten Hin- UND Rückweg des Lichtes zwischen den beiden Spiegeln die Laufzeit erklärt, ist demnach nicht einfach eine Summe oder eine Differenz, sondern durch den oben genannten komplizierteren Ausdruck gegeben.
Zuletzt bearbeitet von dermarkus am 16. März 2006 23:48, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 14. März 2006 21:30 Titel: dermarkus Verfasst am: 14. März 2006 21:30 Titel: |
 |
|
| gustav hat Folgendes geschrieben: | | Aber in der Herleitung oben für 2.) ... |
In der Herleitung für den 2. Fall oben (die ich hier nicht aufgeschrieben habe), fliegt das Licht "schräg", da sehen die Formeln etwas anders aus. Da werden die Geschwindigkeiten also mit dem Satz des Pythagoras addiert.
Diese Herleitung findet man übrigens z.B. unter:
http://homepage.univie.ac.at/Franz.Embacher/SRT/Zeitdilatation.html |
|
 |
gustav
Gast
|
 gustav Verfasst am: 16. März 2006 19:13 Titel: gustav Verfasst am: 16. März 2006 19:13 Titel: |
 |
|
@ dermarkus
vielen Dank !
Dann ist also ( klassisch gesehen ) c'=(c^2 + v^2)^1/2 ( nach Pythagoras ).
Ich glaube jetzt habe ich es geschnallt! |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 16. März 2006 19:30 Titel: dermarkus Verfasst am: 16. März 2006 19:30 Titel: |
 |
|
Ja, das glaube ich auch! 
| gustav hat Folgendes geschrieben: |
Dann ist also ( klassisch gesehen ) c'=(c^2 + v^2)^1/2 ( nach Pythagoras ).
|
Stimmt, das gilt für den Fall der Lichtausbreitung senkrecht zur Bewegungsrichtung.
Denn durch Umformen dieser Gleichung

kommt man gerade wieder auf das von oben für diesen Fall schon bekannte
 |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 16. März 2006 23:56 Titel: dermarkus Verfasst am: 16. März 2006 23:56 Titel: |
 |
|
In der fünften Formel von oben für den 1. Fall, die ich oben mal zitiert habe, hatte ich vergessen, "rueck" statt "hin" zu schreiben.
Und in Folge dessen hatte ich in den Beiträgen, die ich eben editiert habe, ein paar Striche bei den c's und einmal die Bezeichnung Hin- und Rückweg ein bisschen durcheinandergebracht.
Ich hoffe, diese Ungenauigkeiten meinerseits haben dein Verständnis der Beschreibung des 1. Falls nicht zu sehr erschwert, und möglicherweise findest du sie nun in der korrigierten Version noch ein bisschen einleuchtender. |
|
 |
Michisuperfreak
Anmeldungsdatum: 19.12.2006
Beiträge: 36
|
 Michisuperfreak Verfasst am: 08. Jun 2007 19:37 Titel: Michisuperfreak Verfasst am: 08. Jun 2007 19:37 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: |
d+(c'-v)d}{c'^2-v^2}=\frac{2dc'}{c'^2-v^2} =\frac{2d/c'}{1-v^2/c'^2})
|
Sorry, dass ich erst so spät schreibe. Aber hier scheitere ich an der Mathematik!
Bis:

Kann ich dir folgen, aber ich verstehe einfach nicht, was du dann machst!? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Jun 2007 20:11 Titel: as_string Verfasst am: 08. Jun 2007 20:11 Titel: |
 |
|
Hallo!
So, wie man halt Brüche addiert: Hauptnenner finden (hier einfach das Produkt aus beiden Nennern, das funktioniert natürlich so wie so immer), Brüche passend erweitern und die Zähler der erweiterten Brüche addieren. Fertig! Zum Schluß wurde noch mit c'² gekürzt.
Gruß
Marco |
|
 |
Michisuperfreak
Anmeldungsdatum: 19.12.2006
Beiträge: 36
|
 Michisuperfreak Verfasst am: 08. Jun 2007 20:17 Titel: Michisuperfreak Verfasst am: 08. Jun 2007 20:17 Titel: |
 |
|
Also eigentlich habe ich es so gemacht, entweder ich hab mich total doof verrechnet oder ich stehe auf der Leitung.
Zumindest weiß ich jetzt, dass mein Weg nicht falsch war 
Danke!
edit: Mein Hauptnenner ist doch c²-v²? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Jun 2007 20:52 Titel: as_string Verfasst am: 08. Jun 2007 20:52 Titel: |
 |
|
Hallo!
Genau der Hauptnenner steht doch auch da.  Dann musst Du den ersten Zähler mit dem multiplizieren, was im zweiten Nenner steht (das ist der Faktor, mit dem Du den ersten Bruch erweitern musst) und den zweiten Zähler mit dem ersten Nenner. Genau das steht da. Dann musst Du den ersten Zähler mit dem multiplizieren, was im zweiten Nenner steht (das ist der Faktor, mit dem Du den ersten Bruch erweitern musst) und den zweiten Zähler mit dem ersten Nenner. Genau das steht da.
Gruß
Marco
//Edit: OK, bis auf den Strich... 
Zuletzt bearbeitet von as_string am 08. Jun 2007 20:54, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Jun 2007 20:53 Titel: dermarkus Verfasst am: 08. Jun 2007 20:53 Titel: |
 |
|
| Michisuperfreak hat Folgendes geschrieben: |
edit: Mein Hauptnenner ist doch c²-v²? |
Und vergiss den Strich am  nicht, sonst verlierst du bei solchen Rechnungen schnell den Überblick nicht, sonst verlierst du bei solchen Rechnungen schnell den Überblick  |
|
 |
Michisuperfreak
Anmeldungsdatum: 19.12.2006
Beiträge: 36
|
 Michisuperfreak Verfasst am: 09. Jun 2007 12:24 Titel: Michisuperfreak Verfasst am: 09. Jun 2007 12:24 Titel: |
 |
|
Oh gott, mir ist aufgefallen, dass ich auf meinem Blatt Papier irgendwo c² anstannt c' geschrieben habe.
Jetzt ist natürlich alles klar! Danke |
|
 |
|

















 Dann musst Du den ersten Zähler mit dem multiplizieren, was im zweiten Nenner steht (das ist der Faktor, mit dem Du den ersten Bruch erweitern musst) und den zweiten Zähler mit dem ersten Nenner. Genau das steht da.
Dann musst Du den ersten Zähler mit dem multiplizieren, was im zweiten Nenner steht (das ist der Faktor, mit dem Du den ersten Bruch erweitern musst) und den zweiten Zähler mit dem ersten Nenner. Genau das steht da.
