| Autor |
Nachricht |
SchrödingerDerZweite
Gast
|
 SchrödingerDerZweite Verfasst am: 25. Jul 2015 12:15 Titel: Allgemeine Normierung von Wellen SchrödingerDerZweite Verfasst am: 25. Jul 2015 12:15 Titel: Allgemeine Normierung von Wellen |
 |
|
Guten Morgen Physics!
Ich lerne gerade für meine theoretische Quantenmechanik Klausur und bekomm einen Sachverhalt nicht zur Genüge verallgemeinert, leider wurde mir der Sachverhalt bis jetzt auch nicht aus meinem Skript oder Büchern komplett bewusst. Ich hoffe mir kann kann jemand kurz den rechten Pfad zeigen.
Und zwar geht es um Wellenfunktionen, betrachten wir sie der Einfachheit halber in diesem Fall 1-dimensional.
Nun stellt man sich hier ja zunächst ein paar klassischen Problemen, indem man eine einlaufende Welle an einem Rechteckpotential, einem Delta-Potential etc. betrachtet. Ich vermute jedoch der konkrete Fall spielt für meine Frage keine Rolle.
Bei all diesen Aufgaben nutzt man stets die Stetigkeit der Wellenfunktion, sowie deren Ableitung an nicht unendlichen Potentialstufen, aus. Hieraus erhält man ein Gleichungssystem aus dem man die Koeffizienten der Welle in den jeweiligen Teilbereichen herleiten kann. Soweit so gut.
Bei manchen Problemen, z.B. dem Delta-Potential reicht dies jedoch nicht aus, hier setzt man zusätzlich an, dass die Wellenfunktion im unendlichen verschwinden muss, weshalb 2 Koeffizienten 0 werden müssen.
Oder in dem Fall einer einlaufenden Welle von - unendlich an ein Rechteckpotential, wählt man den Koeffizienten der einlaufenden Welle gleich 1 und den der reflektierten Welle im Bereich nach dem Potential gleich 0.
Für Wellen rede ich hier von einem allgemeine Ansatz
 = A_l e^{i k_l x} + B_l e^{-i k_l x} )
(Ich hoffe die Formel fügt sich so ein, verzeiht mir meine Neuheit falls nicht)
Meine Frage die sich mir nicht erklärt ist nun:
Wann führe ich solche ,,eigene Normierungen" ein und wann nicht?
Und wieso verschwindet die Welle manchmal im unendlichen und manchmal nicht?
Ich weiß das Elemente des Hilbertraums zwecks normierbarkeit im unendlichen verschwinden müssen, jedoch fehlt mir der letzte Schritt dahin unterscheiden zu können wann mir welcher Fall vorliegt und wovon das abhängt.
Ich hoffe mir kann jemand das letzte Stückchen erleuchten 
Vielen Dank schon einmal |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Jul 2015 13:21 Titel: TomS Verfasst am: 25. Jul 2015 13:21 Titel: |
 |
|
Leider gibt es in der QM nicht "den" Hilbertraum.
Rein theoretisch wäre das denkbar, denn ein Axiom der QM besagt, dass diese auf einem separablen Hilbertraum (normierbar mit abzählbarer Basis) formuliert wird. Alle derartigen separabelen Hilberträume sind isomorph, d.h. letztlich identifizierbar.
Aber das hilft nichts, denn man möchte ja der Problemstellung angepasste Funktionensysteme benutzen, und da stößt man auch auf verallgemeinerte Hilberträume mit "uneigentlichen Basissystemen" wie ebenen Wellen.
Lassen wir das mal (zunächst) beiseite.
In einem verbreiteten Hilbertraum, dem L2[a,b] der quadratintegrablen Funktionen auf dem Intervall I = [a,b] folgt nicht zwingend, dass diese für I = R im Unendlichen verschwinden müssen. Man kann durchaus quadratintegrable Funktionen definieren, die im Unendlichen nicht verschwinden.
(betrachte eine Funktion bestehend aus Rechtecken endlicher Breite und endlicher Höhe lokalisiert bei den ganzen Zahlen Z; du kannst nun für wachsendes n aus Z die Breite B(n) der Rechtecke schrumpfen lassen, die Höhe H(n) wachsen lassen, so dass für die Norm dennoch ein endliches Ergebnis folgt; das zu berechnende Integral führt für diese aus Rechtecken zusammengesetzten Funktion auf soetwas wie
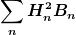
Setze


mit p,q > 0; dann folgt für die Summe

und für

ist diese Summe endlich (für n =1,2,...))
Randbedingungen im Unendlichen folgen also zumeist eher aus praktischen Überlegungen, nicht direkt aus der Hilbertraumstruktur bzw. den Axiomen. Sie spiegeln z.B. Anfangs- bzw. Randbedingungen wieder, die an ein Problem angepasst werden müssen. Sie können auch unmittelbar verletzt sein, wie du z.B. an den ebenen Wellen erkennst.
Im Falle eines abzählbarer Basissystems kenne ich keines, das für die elementare QM relevant wäre, und das im Unendlichen nicht verschwindet. Im Falle eines kompakten bzw. endlichen Intervalls [a,b] kenne ich wiederum kein relevantes Basissystem, das nicht abzählbar und quadratintegrabel wäre.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
SchrödingerDerZweite
Gast
|
 SchrödingerDerZweite Verfasst am: 25. Jul 2015 14:19 Titel: SchrödingerDerZweite Verfasst am: 25. Jul 2015 14:19 Titel: |
 |
|
Hmm.. okay das hat jetzt irgendwie mein Verständnis des mathematischen Grundgerüsts zerstört. Aber das Beispiel erscheint mir einleuchtend, offensichtlich muss eine L2-Funktion nicht im unendlichen verschwinden.
Aber wie ist das physikalische zu deuten? Vielleicht komme ich so meinem Problem auch ein Schritt näher.
Oftmals habe ich gehört, dass die Wellenfunktion für gebundene Zustände welche theoretisch nur für Teilchen Energien <0 auftreten können, im unendlichen verschwinden muss.
Das würde sich mit den Beispielen des negativen Delta-Potentials und des positiven Rechteckpotentials decken.
Bei dem negativen Delta-Potential kann das Teilchen also quasi einen gebundenen Zustand im Bereich des Delta-Peaks eingehen, man nimmt deswegen an, dass die Wellenfunktion im unendlichen verschwindet und normiert sich so seine Welle.
Beim positiven Rechteckpotential kann es keine gebundenen Zustände geben, deswegen muss die Wellenfunktion nicht im unendlichen verschwinden.
Ist meine Betrachtung dieser Fälle jetzt so halbwegs ,,formell" korrekt?
Hätte ich ein negatives Recheckpotential, also einen endlichen Potentialtopf, würde ich folglich nach selbiger Begründung also auch annehmen, dass die Wellenfunktion im unendlichen verschwindet?
Ich finde es jetzt aber schon irgendwie verwirrend, dass dem keine grundlegende mathematische Herangehensweise zugrunde liegt, ich dachte in der Quantenmechanik würde man sich von diesen mathematisch informelleren physikalischen Interpretationen verabschieden  . . |
|
 |
SchrödingerDerZweite
Gast
|
 SchrödingerDerZweite Verfasst am: 25. Jul 2015 15:38 Titel: SchrödingerDerZweite Verfasst am: 25. Jul 2015 15:38 Titel: |
 |
|
|
Mir ist eben noch eingefallen, dass man in der Quantenmechanik ausschließlich stetige Funktionen betrachtet, eine mögliche Unstetigkeit haben wir in der Vorlesung zu einem Widerspruch mit (ohne Gewähr ich bin mir nicht mehr ganz sicher) der Kontinuitätsgleichung geführt. |
|
 |
SchrödingerDerZweite
Gast
|
 SchrödingerDerZweite Verfasst am: 25. Jul 2015 15:58 Titel: SchrödingerDerZweite Verfasst am: 25. Jul 2015 15:58 Titel: |
 |
|
Nachtrag zu meinem letzten Kommentar:
Die Stetigkeit der Wellenfunktion und deren Ableitung folgt über die Schrödingergleichung unter der Annahme eines Potentials mit lediglich endlichen Sprungstellen |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. Jul 2015 18:37 Titel: index_razor Verfasst am: 25. Jul 2015 18:37 Titel: |
 |
|
Meine Gedanken dazu, möglicherweise nicht ganz ausgereift:
| SchrödingerDerZweite hat Folgendes geschrieben: | Hmm.. okay das hat jetzt irgendwie mein Verständnis des mathematischen Grundgerüsts zerstört. Aber das Beispiel erscheint mir einleuchtend, offensichtlich muss eine L2-Funktion nicht im unendlichen verschwinden.
Aber wie ist das physikalische zu deuten? Vielleicht komme ich so meinem Problem auch ein Schritt näher.
|
Zur vollständigen (physikalischen) Charakterisierung eines quantenmechanischen Systems gehört nicht nur die Wahl eines Hilbertraums (der ist, wie bereits angedeutet, durch seine Dimension sowieso weitgehend festgelegt), sondern zumindest auch die Angabe einer Observablenalgebra, insbesondere eines Hamiltonians. Die Frage welche physikalische Relevanz die von TomS skizzierte Wahrscheinlichkeitsamplitude besitzt, läßt sich ansonsten nicht beantworten. Sie gehört z.B. zu keinem System, welchem man ohne weiteres eine kinetische Energie zuordnen kann, denn als solches müßte sie im Definitionsbereich des Operators  liegen. Wellenfunktionen mit dieser Eigenschaft müssen also zumindest mal fast überall differenzierbar sein und eine fast überall differenzierbare Ableitung besitzen. Physikalisch relevante Zustände sind in diesem Zusammenhang also nicht irgendwelche Elemente aus L², sondern aus einem geeigneten Sobolev-Raum. Als solche müssen sie tatsächlich im unendlichen verschwinden. liegen. Wellenfunktionen mit dieser Eigenschaft müssen also zumindest mal fast überall differenzierbar sein und eine fast überall differenzierbare Ableitung besitzen. Physikalisch relevante Zustände sind in diesem Zusammenhang also nicht irgendwelche Elemente aus L², sondern aus einem geeigneten Sobolev-Raum. Als solche müssen sie tatsächlich im unendlichen verschwinden.
| Zitat: |
Oftmals habe ich gehört, dass die Wellenfunktion für gebundene Zustände welche theoretisch nur für Teilchen Energien <0 auftreten können, im unendlichen verschwinden muss.
|
Ja, die Bewegung von gebundenen Zuständen ist räumlich beschränkt. Denn solche Zustände gehören zum diskreten Spektrum des Hamiltonoperators ) . Sie müssen also (als echte Eigenvektoren) quadratintegrabel und hinreichend glatt sein. (Es stimmt übrigens nicht, daß gebundene Zustände eine Energie < 0 besitzen müssen. Es kann theoretisch auch gebundene Zustände mit positiver Energie geben.) . Sie müssen also (als echte Eigenvektoren) quadratintegrabel und hinreichend glatt sein. (Es stimmt übrigens nicht, daß gebundene Zustände eine Energie < 0 besitzen müssen. Es kann theoretisch auch gebundene Zustände mit positiver Energie geben.)
| Zitat: |
Das würde sich mit den Beispielen des negativen Delta-Potentials und des positiven Rechteckpotentials decken.
Bei dem negativen Delta-Potential kann das Teilchen also quasi einen gebundenen Zustand im Bereich des Delta-Peaks eingehen, man nimmt deswegen an, dass die Wellenfunktion im unendlichen verschwindet und normiert sich so seine Welle.
Beim positiven Rechteckpotential kann es keine gebundenen Zustände geben, deswegen muss die Wellenfunktion nicht im unendlichen verschwinden.
|
Die Logik ist, denke ich, eher andersrum: Eigenzustände von H sind quadratsummierbar, hinreichend glatt und verschwinden deshalb im unendlichen.
Nichtgebundene Zustände gehören zum kontinuierlichen Spektrum des Hamiltonoperators. Es gibt in diesem Fall keine Hilbertraumvektoren mit entsprechender Energie. Das heißt, bereits die Quadratsummierbarkeit ist verletzt. In diesem Fall muß man den Hilbertraum verlassen und zu Distributionen über einem geeigneten Teilraum von L² übergehen. Für den Fall des Hamiltonoperators  liefert das z.B verallgemeinerte Eigenfunktionen liefert das z.B verallgemeinerte Eigenfunktionen  . Die sind natürlich weder aus L² noch verschwinden sie im unendlichen. Dasselbe gilt i.A. auch für Streuzustände in hinreichend normalen Potentialen. . Die sind natürlich weder aus L² noch verschwinden sie im unendlichen. Dasselbe gilt i.A. auch für Streuzustände in hinreichend normalen Potentialen.
| Zitat: |
Ich finde es jetzt aber schon irgendwie verwirrend, dass dem keine grundlegende mathematische Herangehensweise zugrunde liegt, ich dachte in der Quantenmechanik würde man sich von diesen mathematisch informelleren physikalischen Interpretationen verabschieden  . . |
Es gibt schon eine grundlegende mathematische Herangehensweise. Verwirrend ist sie aber trotzdem. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Jul 2015 08:06 Titel: TomS Verfasst am: 26. Jul 2015 08:06 Titel: |
 |
|
Die Stetigkeit bzw. Glattheit ist kein Problem. Man kann die o.g. Funktion auch glätten, z.B. indem man geeignete Gaußsche Wellenpakete mit wachsender Höhe und schrumpfender Breite an ihre Stelle setzt.
Das kontinuierliche Spektrum von Operatoren wie x, p, H. usw. ist i.A. nicht mit quadratintegrablen Eigenfunktionen verknüpft. D.h. zur Behandlung dieser Funktionen muss man einen geeigneten neuen Hilbertraum einführen, um diese Funktionen als "Lösungen" auffassen zu dürfen.
Die Wahl des Hilbertraumes ist physikalisch motiviert, nicht mathematisch. Dies resultiert im Wesentlichen aus der Forderung, dass <a|b> eine physikalisch interpretierbare Wahrscheinlichkeitsamplitude sein soll. Die Norm <a|a> = 1 bedeutet ja, dass wenn ein Zustand |a> vorliegt, die Wsk., dass dieser Zustand |a> vorliegt, gleich 1 ist. Für ebene Wellen mit Impuls k ist das im L2 offensichtlich undefiniert. Es ist aber physikalisch oft ausreichend, andere Amplituden zu betrachten, z.B. die Streuung einer ebenen Welle |k> in einen anderen Zustand |a> durch eine Wechselwirkung T, d.h. <a|T|k>.
Man kann die jeweils benötigten Hilberträume mathematisch präzise fassen. Das nützt jedoch nichts, wenn man die zugrundeliegende Physik nicht verstanden hat.
Die mathematische Theorie der Sobolev- und Schwartz-Räume wurde in den 30iger und 40iger Jahren ausgearbeitet; da konnten die Physiker sie schon längst "benutzen" ... |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Jul 2015 08:12 Titel: index_razor Verfasst am: 27. Jul 2015 08:12 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Die Stetigkeit bzw. Glattheit ist kein Problem. Man kann die o.g. Funktion auch glätten, z.B. indem man geeignete Gaußsche Wellenpakete mit wachsender Höhe und schrumpfender Breite an ihre Stelle setzt.
|
Das von mir im letzten Beitrag nicht ganz durchsichtig formulierte Problem ist das des Definitionsbereichs von Operatoren 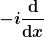 und und  . Weder deine ursprüngliche Rechtecksfunktion noch der "stückweise" Gauß liegen, denke ich, in geeigneten Definitionsbereichen. Dazu müßten sie den Operator als hermitesche Selbstabbildung auf L² definieren, insbesondere müssen also die ersten beiden Ableitungen f.ü. existieren, in L² liegen und es muß . Weder deine ursprüngliche Rechtecksfunktion noch der "stückweise" Gauß liegen, denke ich, in geeigneten Definitionsbereichen. Dazu müßten sie den Operator als hermitesche Selbstabbildung auf L² definieren, insbesondere müssen also die ersten beiden Ableitungen f.ü. existieren, in L² liegen und es muß
^k g = \int ((-i\frac{\dd}{\dd x})^k f)^\star g
<br />
)
für die ersten beiden Ableitungen k = 1,2 gelten.
Wenn man alle diese Forderungen zusammennimmt, landet man bei Funktionen, die zumindest stetig sein müssen, soweit ich weiß sogar absolutstetig mit absolutstetiger Ableitung. Aus der Symmetrieeigenschaft folgt insbesondere
 und und  für für  . . |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Jul 2015 10:30 Titel: TomS Verfasst am: 27. Jul 2015 10:30 Titel: |
 |
|
Gaußfunktionen sind kein Problem im L². Die Fourier-Trf. auf dem L² hat Hermitefunktionen als Eigenfunktionen, damit liegen die Probleme an den Operatoren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Jul 2015 10:38 Titel: index_razor Verfasst am: 27. Jul 2015 10:38 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Gaußfunktionen sind kein Problem im L². Die Fourier-Trf. auf dem L² hat Hermitefunktionen als Eigenfunktionen, damit liegen die Probleme an den Operatoren. |
Gaußfunktionen sind kein Problem, weder für den L² noch für die genannten Operatoren. Gaußfunktionen verschwinden insbesondere auch im Unendlichen. Du hattest eine andere Konstruktion vorgeschlagen, die weder stetig war noch im unendlichen verschwinden sollte. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Jul 2015 12:48 Titel: TomS Verfasst am: 27. Jul 2015 12:48 Titel: |
 |
|
Ja, ich hatte vorgeschlagen, die o.g. Summe über Rechtecke in eine Summe über Gaußfunktionen zu ersetzen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Jul 2015 17:08 Titel: index_razor Verfasst am: 27. Jul 2015 17:08 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Ja, ich hatte vorgeschlagen, die o.g. Summe über Rechtecke in eine Summe über Gaußfunktionen zu ersetzen. |
Ok, das macht die Funktion unendlich oft differenzierbar, aber das ist doch nicht der Punkt. Mein Einwand war: Sie ist trotzdem nicht aus dem Definitionsbereich eines hermiteschen Operators 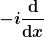 bzw. bzw.  . Oder wie würdest du normalerweise beweisen, daß es sich bei diesen Differentialoperatoren um hermitesche Operatoren auf L²(R) handelt? Dafür braucht man doch . Oder wie würdest du normalerweise beweisen, daß es sich bei diesen Differentialoperatoren um hermitesche Operatoren auf L²(R) handelt? Dafür braucht man doch  im unendlichen, oder nicht? im unendlichen, oder nicht? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Jul 2015 18:08 Titel: TomS Verfasst am: 27. Jul 2015 18:08 Titel: |
 |
|
Ja natürlich
| TomS hat Folgendes geschrieben: | | Die Stetigkeit bzw. Glattheit ist kein Problem. Man kann die o.g. Funktion auch glätten, z.B. indem man geeignete Gaußsche Wellenpakete mit wachsender Höhe und schrumpfender Breite an ihre Stelle setzt. |
| TomS hat Folgendes geschrieben: | | Gaußfunktionen sind kein Problem im L² ... damit liegen die Probleme an den Operatoren. |
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Jul 2015 19:11 Titel: index_razor Verfasst am: 27. Jul 2015 19:11 Titel: |
 |
|
Tut mir leid, ich verstehe nicht, worauf du hinaus willst. Mir ging es nur um die Beantwortung der Frage, warum man nur stetige im unendlichen verschwindende Lösungen der Schrödingergleichung betrachtet und wie in diesem Zusammenhang deine Summe von Rechtecken bzw. Gaußfunktionen einzuordnen ist, die (glatt oder nicht-glatt) eben nicht im unendlichen verschwinden. Ich denke, der Grund warum man sie nicht betrachtet, ist, daß, obwohl sie im L² liegen, sie nicht zum Definitionsbereich von H oder p gehören. Das kannst du nun genauso gut als Problem dieser Operatoren, wie als Problem der fraglichen Elemente aus L² betrachten. Aber an den Operatoren wirst du nicht viel ändern können, du kannst nur eine vernünftigen Teilmenge von L² als Definitionsbereich für sie wählen.
| TomS hat Folgendes geschrieben: | | Die Stetigkeit bzw. Glattheit ist kein Problem. Man kann die o.g. Funktion auch glätten, z.B. indem man geeignete Gaußsche Wellenpakete mit wachsender Höhe und schrumpfender Breite an ihre Stelle setzt. |
Also ist -- das zeigt die Summe von Gaußfunktionen -- Glattheit nicht das einzige Problem. Aber es ist ein Problem, denn nicht hinreichend glatte Funktionen funktionieren auch nicht ohne weiteres (auch wenn sie im unendlichen verschwinden).
| TomS hat Folgendes geschrieben: | | Gaußfunktionen sind kein Problem im L² ... damit liegen die Probleme an den Operatoren. |
Ja, ok, dann sind eben die Operatoren schuld. Aber wer auch immer nun schuld ist, ist doch nicht so wichtig wie die Frage, wie man nun einen Satz von Observablen, inklusive ihrer Definitionsbereiche im L² konstruieren kann, der für das fragliche quantenmechanische Problem adäquat ist. Welche Randbedingungen sind nun zur Lösung dieses Problems an die Wellenfunktionen zu stellen? Existenz der L²-Norm reicht dafür im allgemeinen nicht aus. (Dies sollte klar sein, denn die relevanten Operatoren sind notorisch nicht überall definiert.) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Jul 2015 19:50 Titel: TomS Verfasst am: 27. Jul 2015 19:50 Titel: |
 |
|
Ja, ich stimme zu. Ich weiß nicht, wie du darauf kommst, ich würde das anders sehen.
Ich wollte lediglich darauf hinweisen, das der Grund für das Verschwinden der Funktionen im Unendlichen nichts mit der Quadratintegrabilität zu tun hat. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 27. Jul 2015 20:02 Titel: Jayk Verfasst am: 27. Jul 2015 20:02 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Das kontinuierliche Spektrum von Operatoren wie x, p, H. usw. ist i.A. nicht mit quadratintegrablen Eigenfunktionen verknüpft. D.h. zur Behandlung dieser Funktionen muss man einen geeigneten neuen Hilbertraum einführen, um diese Funktionen als "Lösungen" auffassen zu dürfen.
|
Dem möchte ich aus zwei Gründen widersprechen:
- Verallgemeinerte Eigenzustände aus S' liegen nicht in einem Hilbertraum (mir ist aber nicht entgangen, daß wir schonmal eine Diskussion hatten, ob es einen größeren Hilbertraum gibt, der S' beinhaltet)
- Niemand garantiert, daß es für selbstadjungierte Operatoren auf dem L² immer eine Entwicklung nach Eigenzuständen aus L² und aus S' gibt.
Mir ist noch ein anderes Argument eingefallen, warum es nichts bringt, einen anderen Hilbertraum einzuführen: Das Skalarprodukt hat ja, wie Du schon gesagt hast, eine physikalische Motivation. Also sollte man, wenn überhaupt, nach einer isometrischen Einbettung fragen (also wenn man nach einem größeren Hilbertraum fragt, sollte sich der kleinere isometrisch einbetten lassen). Das wird aber nicht funktionieren, da ja jeder metrische Raum einen eindeutigen (bis auf Isometrie) Abschluß hat (und ein Hilbertraum ist klarerweise sein eigener Abschluß). Verzichtet man auf die Forderung nach Isometrie, so wird sich das Skalarprodukt ändern. Das ist, wie schon gesagt, physikalisch problematisch, aber es gibt auch ein mathematisches Problem damit: Damit würde ein Operator im neuen (größeren) Hilbertraum auch einen anderen adjungierten Operator bekommen und ein hermitescher Operator nicht hermitesch bleiben.
Der Sobolevraum W² ist wohl als Menge der geeignete Definitionsbereich für den Impulsoperator [sorry, das ist natürlich falsch; hab das mit dem Laplace-Operator verwechselt, für den ist das zutreffend], wenn er als Teilmenge des L² aufgefaßt wird. Zufällig ist er selbst ein Hilbertraum, aber er ist sicher nicht "der Hilbertraum" im Sinne der Postulate der QM, denn er hat das falsche Skalarprodukt. Der Impulsoperator ist hermitesch über dem L², nicht über W².
@index_razor: Ich weiß nicht, ob jede Sobolevfunktion im Unendlichen verschwindet. Anschaulich würde ich das vermuten, aber mir fällt kein Beweis ein und ich habe diese Aussage auch nirgends gefunden (habe bei Teschl "Mathematical Methods in Quantum Mechanics", in Reed/Simon I+II, Wikipedia und in einem alten Funktionalanalysis-Skript gesucht). Und ich denke, wenn so eine wichtige Aussage gelten würde, würde man sie doch irgendwo finden, oder? |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 27. Jul 2015 20:39 Titel: Jayk Verfasst am: 27. Jul 2015 20:39 Titel: |
 |
|
Die Aussage  \vert \to 0) für für  ist auf jeden Fall richtig (über ist auf jeden Fall richtig (über  zumindest). Man kann nämlich zeigen, daß die Fouriertransformierte einer Sobolev-Funktion integrierbar ist, und dann das Riemann-Lebesgue-Lemma anwenden. Hab den Beweis in einem QM-Skript von einem mathematischen Physiker gefunden. zumindest). Man kann nämlich zeigen, daß die Fouriertransformierte einer Sobolev-Funktion integrierbar ist, und dann das Riemann-Lebesgue-Lemma anwenden. Hab den Beweis in einem QM-Skript von einem mathematischen Physiker gefunden.
Skizze:
Es gilt  und somit auch und somit auch
 \vert \hat \psi ( k ) \vert^2\,dk< \infty) . Da . Da ^{- 1/2}) (jedenfalls im Ein-, Zwei- und Dreidimensionalen) eine L²-Funktion ist, kann mit der Minkowski-Ungleichung gezeigt werden, daß (jedenfalls im Ein-, Zwei- und Dreidimensionalen) eine L²-Funktion ist, kann mit der Minkowski-Ungleichung gezeigt werden, daß  eine L¹-Funktion ist. eine L¹-Funktion ist.
PS: Um das für den R³ zeigen zu können, braucht man aber wirklich zweimal schwache Differenzierbarkeit. Sonst wird aus der 4 eine 2 und der Beweis funktioniert nur noch für R¹... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Jul 2015 21:28 Titel: TomS Verfasst am: 27. Jul 2015 21:28 Titel: |
 |
|
@Jayk: du widersprichst dem Begriff "Hilbertraum" im zweiten Teil meiner Aussage; OK, einverstanden. Der Rest passt aber:
Das kontinuierliche Spektrum von Operatoren wie x, p, H. usw. ist i.A. nicht mit quadratintegrablen Eigenfunktionen verknüpft. D.h. zur Behandlung dieser Funktionen muss man einen geeigneten neuen Funktionenraum einführen, um diese Funktionen als "Lösungen" auffassen zu dürfen.
Noch eine generelle Anmerkung: dass man Eigenfunktionen zu x, p sucht bzw. verwendet, ist nicht physikalisch motivierbar, lediglich häufig mathematisch praktisch. Ebene Wellen sind sicher unphysikalisch, da nicht durch räumlich und zeitlich lokalalisierte Prozesse präparierbar; das gilt auch für Streuzustände in anderen Potentialen. Insofern ist es eigtl. überhaupt nicht notwendig, sich damit zu befassen, da in physikalischen Matrixelementen

diese unphysikalischen Zustände nicht vorkommen. Wenn aber diese Funktionen nicht zwingend physikalisch sind, besteht auch kein Grund, dass ein Hilbertraum vorliegen muss. Die QM assoziiert gemäß Axiom Hilbertraumelemente mit physikalischen Zuständen eines Systems.
Allerdings ist eine praktische Behandlung vieler Probleme mit rein physikalischen Zuständen bzw. Wellenpakten unhandlich, und daher stammt letztlich die Verwendung derartiger Funktionen und verallgemeinerter Funktionenräume. Die QM verbietet diese nicht als Hilfskonstruktion. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 28. Jul 2015 00:33 Titel: Jayk Verfasst am: 28. Jul 2015 00:33 Titel: |
 |
|
@TomS: Ist schon okay. Es schien mir nur so, als wolltest Du dieses Vorgehen irgendwie auf den Formalismus des "abstrakten Hilbertraums" im Sinne der Postulate der QM zurückführen, was mir mindestens eine sehr freie Auslegung zu sein schien.
Es war nicht mein Anliegen, Deine Aussage grundsätzlich zu kritisieren.
Allerdings bleibt: Ich bezweifle, daß dieses Vorgehen mit verallgemeinerten Eigenfunktionen allgemein durchführbar ist. Goldhorn, Heinz und Kraus schreiben in "Moderne mathematische Methoden der Physik" (Band 2), daß dieses Verfahren für "bestimmte Klassen" von Operatoren funktioniert. Daraus schließe ich, daß es Gegenbeispiele geben sollte. Ich kenne aber keines und es kann natürlich auch sein, daß man das Verfahren bisher nur für bestimmte Klassen bewiesen hat und es trotzdem allgemein gültig ist.
Allerdings verstehe ich auch nicht, wieso der Spektralsatz in so wenigen QM-Vorlesungen formuliert wird. Ich finde die physikalische Einsicht, die man dadurch gewinnt, sehr wertvoll. Die Idee, einer Menge von Meßwerten einen Projektionsoperator zuzuordnen, ist doch eine 1:1-Übertragung der Idee "Kollaps der Wellenfunktion". Die Idee der verallgemeinerten Eigenfunktionen wirkt für mich eher künstlich (zum Rechnen ist das sicher ein sehr praktischer Trick, allerdings verschleiert er meiner Meinung nach die Physik). |
|
 |
HeiligerJesus
Gast
|
 HeiligerJesus Verfasst am: 28. Jul 2015 04:52 Titel: HeiligerJesus Verfasst am: 28. Jul 2015 04:52 Titel: |
 |
|
|
Was fur ein Geschwafel. @TE entweder du liest das Buch von John von Neumann durch , oder du fragst wo anders. Hier hat keiner Ahnung von QM. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jul 2015 07:08 Titel: TomS Verfasst am: 28. Jul 2015 07:08 Titel: |
 |
|
| HeiligerJesus hat Folgendes geschrieben: | | Was fur ein Geschwafel. @TE entweder du liest das Buch von John von Neumann durch , oder du fragst wo anders. Hier hat keiner Ahnung von QM. |
Danke für die qualifierte Bemerkung.
Konkrete Frage: was schreibt von Neumann in seinem Buch über Sobolev- und Schwartz-Räume, die ja erst nach dessen Veröffentlichung untersucht wurden?

@Jayk: der Spektralsatz wird schon behandelt; aber eine Verbindung zum Kollapsposulat sehe ich nur sehr indirekt, denn wie oben angemerkt ist das kontinuierliche Spektrum insofern unphysikalisch, als diese Zustände nicht präparierbar sind.
PS.: da ich die Everett-Interpretation befürworte, halte ich den Kollaps selbst ebenfalls für unphysikalisch
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2015 10:07 Titel: index_razor Verfasst am: 28. Jul 2015 10:07 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: |
@index_razor: Ich weiß nicht, ob jede Sobolevfunktion im Unendlichen verschwindet. Anschaulich würde ich das vermuten, aber mir fällt kein Beweis ein und ich habe diese Aussage auch nirgends gefunden (habe bei Teschl "Mathematical Methods in Quantum Mechanics", in Reed/Simon I+II, Wikipedia und in einem alten Funktionalanalysis-Skript gesucht). Und ich denke, wenn so eine wichtige Aussage gelten würde, würde man sie doch irgendwo finden, oder? |
Das gilt, denke ich, nicht für jede Sobolev-Funktion. Ist nicht die schon diskutierte Summe von Rechtecken bereits ein Gegenbeispiel?
Allerdings war meine Idee, daß man für die Definitionsbereiche von Impuls und kinetischer Energie auf jeden Fall das verschwinden im unendlichen fordern müsse, um die Symmetrie der Differential-Operatoren zu gewährleisten. Dann müßte m.E. sogar  im R³ gelten. im R³ gelten.
P.S.: Ich verstehe deine Beweisskizze nicht so recht. Folgt daraus nicht nur das  existiert? Das reicht doch nicht, um |f|->0 zu folgern, oder verstehe ich das falsch? existiert? Das reicht doch nicht, um |f|->0 zu folgern, oder verstehe ich das falsch?
P.P.S. achso, das ist das Riemann-Lebesgue-Lemma. Hm, dann folgt wohl, daß die Rechtecksumme keine Sobolev-Funktion ist. Mir ist aber grad nicht klar wieso nicht. |
|
 |
HeiligerJesus
Gast
|
 HeiligerJesus Verfasst am: 28. Jul 2015 18:20 Titel: HeiligerJesus Verfasst am: 28. Jul 2015 18:20 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | HeiligerJesus hat Folgendes geschrieben: | | Was fur ein Geschwafel. @TE entweder du liest das Buch von John von Neumann durch , oder du fragst wo anders. Hier hat keiner Ahnung von QM. |
Danke für die qualifierte Bemerkung.
Konkrete Frage: was schreibt von Neumann in seinem Buch über Sobolev- und Schwartz-Räume, die ja erst nach dessen Veröffentlichung untersucht wurden?

@Jayk: der Spektralsatz wird schon behandelt; aber eine Verbindung zum Kollapsposulat sehe ich nur sehr indirekt, denn wie oben angemerkt ist das kontinuierliche Spektrum insofern unphysikalisch, als diese Zustände nicht präparierbar sind.
PS.: da ich die Everett-Interpretation befürworte, halte ich den Kollaps selbst ebenfalls für unphysikalisch |
Das hat nur etwas mit der Philosophie zu tun mit der man an die Sache rangeht. Sonst nix.Aber ihr könnt ja noch so lange um den heisen Brei reden, und dieser jayk ist echt am schlimmsten. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jul 2015 18:22 Titel: TomS Verfasst am: 28. Jul 2015 18:22 Titel: |
 |
|
wenn du etwas Qualifiziertes zu sagen hast, dann darfst du's gerne tun; bisher hast du nur gesagt, dass du ein Buch gelesen hast, das haben viele ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 28. Jul 2015 21:47 Titel: jh8979 Verfasst am: 28. Jul 2015 21:47 Titel: |
 |
|
| HeiligerJesus hat Folgendes geschrieben: |
Das hat nur etwas mit der Philosophie zu tun mit der man an die Sache rangeht. Sonst nix.Aber ihr könnt ja noch so lange um den heisen Brei reden, und dieser jayk ist echt am schlimmsten. |
Nur mal so als Warnung (als Moderator): Ich finde Deine unhaltbaren Beleidigungen hier gar nicht lustig. Wenn Du also wirklich beitragen willst, dann reiss Dich zusammen und begründe was Du hier schreibst, ansonsten seh' ich kein gutes Ende... |
|
 |
|
|

















 .
.