| Autor |
Nachricht |
Ardente04
Gast
|
 Ardente04 Verfasst am: 03. Jun 2011 20:12 Titel: Herleitung der Wellenfunktion für stehende Wellen Ardente04 Verfasst am: 03. Jun 2011 20:12 Titel: Herleitung der Wellenfunktion für stehende Wellen |
 |
|
Meine Frage:
Hallo,
Ich soll mir Eigenschwingungen einer Saite angucken und dabei näher auf die stehende Welle eingehen. Daraus soll ich eine Formel entwickeln. Ich hab in einem Physikbuch eine Herleitung für die Formel  gefunden. Diese sieht wie folgt aus: gefunden. Diese sieht wie folgt aus:
Ein von außen angeregter Oszillator ist der Ursprung der Welle. Die Auslenkung lässt sich in Abhängigkeit von der Zeit t durch eine Cosinusfunktion darstellen:
= A1*cos(wt)) [A1 = Amplitude ; w = Phasengeschwindigkeit] [A1 = Amplitude ; w = Phasengeschwindigkeit]
Nehmen wir nun einen weiteren Oszillator, welcher vom Ursprung der Schwingung den Abstand x hat. Die dadurch entstehende Phasenverschiebung beträgt:

Ein beliebiger Oszillator lässt sich daher, in Anhängigkeit von der Zeit t und der Position x, darstellen:
= A1*cos(wt-kx) )
Wenn genau so eine Welle reflektiert wird, entsteht eine stehende Welle. Die Funktion der reflektierten Weller ist ähnlich, bloß das sich das Vorzeichen bei der Phasenverschiebung nach ?+kx? ändert. Eigentlich müsste noch ? hinzukommen. Bei einer Reflexion der Welle an einem festen Ende, sprich 180°, ist ? jedoch = 0 und kann vernachlässigt werden.
Die stehende Welle entsteht dann durch die Überlagerung der ankommenden und der reflektierten Welle. Es ergibt sich:
= A1*cos(wt-kx)+ A2*cos(wt+kx))
Die Welle wird vollständig reflektiert. D.h. die Amplitude A = A1 = A2 außerdem ist die Phasenverschiebung = 0.
Addieren wir die obere Formel erhalten wir:
= 2A*cos(wt)*cos(kx))
Damit ergibt sich an jedem Punkt x eine Schwingung mit der Amplitude )
Daraus lassen sich Bedingungen für Schwingungsknoten und Schwingungsbäuche herleiten:
Schwingungsbäuche:
 = 1)


Es befinden sich in Abständen von einer halben Wellenlänge Schwingungsbäuche.
Schwingungsknoten:
= 0)
\pi )
\frac{\lambda }{2} )
Da zwei feste Enden existieren, muss die Länge der Saite genau ein ganzzahliges Vielfaches der halben Wellenlänge haben.

Drückt man die Wellenlänge mit der Formel  aus, ergibt sich: aus, ergibt sich:

So ganz schön langer Text^^
Aber dazu habe ich jetzt ein paar Fragen:
1. Wieso fange ich mit eine Cosinusfunktion an?
2. Bei der Phasenverschiebung und den Schwingungsknoten bzw. Schwingungsbäuchen taucht immer dieses  auf. Wo kommt das jetzt auf einmal her? auf. Wo kommt das jetzt auf einmal her?
2.1. Daher verstehe ich auch die Formeln für die Schwingungsknoten bzw. Schwingungsbäuchen nicht.
Meine Ideen:
1. Ich denk mir, dass sich die Schwingung in einer cosinusform ausbreitet.
2. Vielleicht ist das ja eine festgelegte Formel, welche eine Phasenverschiebung darstellt.
Bei beiden bin ich mir aber absolut nicht sicher! Deshalb wäre es echt toll, wenn mir jemand helfen könnte! |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 04. Jun 2011 19:54 Titel: schnudl Verfasst am: 04. Jun 2011 19:54 Titel: |
 |
|
Ich glaube das wichtigste für dich wäre die Erkenntnis, dass die allgemeine Lösung der Differentialgleichung einer Saite aus einer Überlagerung harmonischer Wellen besteht, die sich entweder in positiver oder negativer Richtung ausbreiten:
}_{\omega} (x;t) = A_k \cos(\omega t - kx)+B_k \sin(\omega t - kx))
}_{\omega} (x;t) = a_k \cos(\omega t + kx)+b_k \sin(\omega t + kx))
Die allgemeine Lösung für eine gegebene Frequenz ("Mode") ist also die Überlagerung aus einer hin- mit einer rücklaufenden Welle:
 = f^{(+)}_{\omega} (x;t) + f^{(-)}_{\omega} (x;t) )
Die "Wellenzahl" k ist dabei ein Parameter, welcher mit der Winkelgeschwindigkeit in der folgender Beziehung steht:

Die allgemeine Lösung einer schwingenden Saite ist daher eine Überlagerung dieser Moden mit verschiedenen Kreisfrequenzen:
 = \sum_\omega (f^{(+)}_{\omega} (x;t) + f^{(-)}_{\omega} (x;t)) )
Die Wellenlänge für eine Mode ist definiert als jener x-Abstand, für den
 = f_\omega (x+\lambda;t) )
wenn du das einsetzt, bekommst du

bzw.
}_{\omega} (x;t) = A_k \cos(\omega t - \frac{2 \pi}{\lambda}x)+B_k \sin(\omega t - \frac{2 \pi}{\lambda}x))
}_{\omega} (x;t) = a_k \cos(\omega t + \frac{2 \pi}{\lambda}x)+b_k \sin(\omega t + \frac{2 \pi}{\lambda}x))
Die möglichen Eigenschwingungen (und damit die möglichen Moden) der beidseitig eingespannten Saite der Länge L erhält man durch die Randbedingungen
 = 0)
 = 0)
welche die Auswahl der Koeffizienten A, B, a, b stark einschränken und so zu stehenden Wellen Anlass geben.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ardente
Gast
|
 Ardente Verfasst am: 06. Jun 2011 12:02 Titel: Ardente Verfasst am: 06. Jun 2011 12:02 Titel: |
 |
|
Danke für deine Antwort!
Aber ich muss am Ende auf die Formel  kommen. Ich habe meinen Lehrer gefragt, ob meine Herleitung so ok ist, er darf mir zwar nicht viel sagen, meinte aber, dass die Herleitung etwas komplizierter ist als erwartet bzw. gefordert. Das Ergebnis ist allerdings so richtig. Für meine Prüfung ist es sehr wichtig, dass ich die Formel gut verstehe. Der allgemeine Aufbau ist mir, auch durch deine Antwort, eigentlich klar. kommen. Ich habe meinen Lehrer gefragt, ob meine Herleitung so ok ist, er darf mir zwar nicht viel sagen, meinte aber, dass die Herleitung etwas komplizierter ist als erwartet bzw. gefordert. Das Ergebnis ist allerdings so richtig. Für meine Prüfung ist es sehr wichtig, dass ich die Formel gut verstehe. Der allgemeine Aufbau ist mir, auch durch deine Antwort, eigentlich klar.
Nur wenn ich versuche mir selber die Formel zu erklären hakt es bei mir an den oben beschriebenen Stellen. Wenn ich wüsste, warum ich mit cos anfange und woher dieses 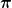 kommt, verstehe ich die Herleitung ganz. kommt, verstehe ich die Herleitung ganz. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 06. Jun 2011 15:52 Titel: schnudl Verfasst am: 06. Jun 2011 15:52 Titel: |
 |
|
Wenn du die Überlagerung für die hin- und rücklaufenden Wellen einsetzt, wirst du feststellen, dass aus der Randbedingung bei x=0 folgt

und

sodaß überbleibt
 = 2 (A\sin \omega t -B \cos \omega t ) \cdot \sin kx)
Wenn der Ausdruck für x=L ebenfalls Null werden soll (2. Randbedingung), so folgt daraus

bzw.

Das kann man dann schreiben als
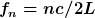
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ardente
Gast
|
 Ardente Verfasst am: 09. Jun 2011 11:14 Titel: Ardente Verfasst am: 09. Jun 2011 11:14 Titel: |
 |
|
Ok, die Formel wird mir immer klarer^^
Aber ein paar Fragen hab ich doch noch.
Um auf deine erste Antwort zurück zu kommen:
| Zitat: | Die Wellenlänge für eine Mode ist definiert als jener x-Abstand, für den = fw (x + \lambda ;t) )
wenn du das einsetzt, bekommst du

|
Da kann ich nicht ganz folgen. Wo setzt ich da was ein?
Wenn du mir diese Stelle etwas genauer erklären könntest, wäre ich dir sehr dankbar.
Ansonsten habe ich die Formel eigentlich im Großen und Ganzen verstanden 
Danke! |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 09. Jun 2011 12:45 Titel: schnudl Verfasst am: 09. Jun 2011 12:45 Titel: |
 |
|
betrachte die Funktion
 = \cos(\omega t - kx))
An der Stelle x=x0 gibt das denn Wert
 = \cos(\omega t - kx_0))
Nun, wo (für welche x) wird diese Funktion für gleiches t den gleichen Funktionswert liefern? Da cos() periodisch in 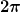 ist, wird ist, wird
 = \cos(\omega t - kx_0-n 2 \pi) = \cos(\omega t - kx_0))
also ist die Periode in x (=Wellenlänge)

_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ardente
Gast
|
 Ardente Verfasst am: 13. Jun 2011 20:15 Titel: Ardente Verfasst am: 13. Jun 2011 20:15 Titel: |
 |
|
Danke! Du hast mir wirklich sehr geholfen!
Eine letzte kleine Frage:
Das "wt" in den Klammern, wofür steht das?
Ich such die ganze Zeit, welche Bedeutung die Variable hat.
Ich bin auf die Periodendauer gestoßen. Ist das richtig? |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 13. Jun 2011 21:16 Titel: schnudl Verfasst am: 13. Jun 2011 21:16 Titel: |
 |
|
 ist die Kreisfrequenz: ist die Kreisfrequenz:
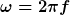
und wird in 1/s angegeben. f ist die Frequenz in Hz oder 1/s
Die Periodendauer T ist
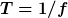
 hat die Größe eines Winkels (in rad) und beschreibt die momentane Phase der Schwingung. Während einer Periodendauer ändert sich der Winkel um hat die Größe eines Winkels (in rad) und beschreibt die momentane Phase der Schwingung. Während einer Periodendauer ändert sich der Winkel um 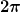 , also , also

oder

_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
|
|
















