| Autor |
Nachricht |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 06. Jul 2004 15:47 Titel: Herleitung der Relativität von Energie und Masse Neko Verfasst am: 06. Jul 2004 15:47 Titel: Herleitung der Relativität von Energie und Masse |
 |
|
Hier, wie versprochen die Herleitung der Relativität von Energie und Masse:
Transformieren der Kraft
Grundgleichung der Mechanik: 
Falls sich Körper mit  bewegt, ist diese Gleichung nicht mehr gültig, bewegt, ist diese Gleichung nicht mehr gültig,  ist zu transformieren: ist zu transformieren:
\,=\,\frac{dm}{dt}\,v\,+\,\frac{dv}{dt}\,m\,=\,\frac{dm}{dt}\,v\,+\,m\,\cdot\,a\,=\,\frac{dm}{dt}\,v\,+\,m\,\cdot\,a\,=\,\frac{dm}{dv}\,(\,\frac{dv}{dt}\,v\,)\,+\,m\,\cdot\,a\,=\,\frac{dv}{dt}\,\frac{dm}{dv}\,v\,+\,m\,\cdot\,a\,=\,a\,(\frac{dm}{dv}\,v\,+\,m\,))
(1)
mit
\,=\,\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^2}}}\, \Rightarrow\,\frac{dm}{dv}\,=\,m_{0}\,\cdot\,\frac{\frac{v}{c^2}}{(\sqrt{1-\frac{v^{2}}{c^{2}}})^{-3}}\,=\,m_{0}\,\cdot\,\frac{v}{c^{2}}\sqrt{\gamma^{3}}) (2) (2)
damit ist (2) in (1)
\,=\,a\,\cdot(\,m_{0}\,\cdot\,\frac{v^{2}}{c^{2}}\,\cdot\,\gamma^{3}\,+\,m_{0}\,\cdot\,\gamma\,))
^{3}}\,+\,\frac{1}{\sqrt{\cdot\cdot\cdot}}\,))
Hauptnenner bilden:
\,=\,a\cdot\,m_{0}\cdot\gamma^{3}) (3) (3)
In
 (3) (3)
die transformierte Kraft einsetzen ((3) in (4)):
^{3}}\,ds\,=\,\int\limits^{s_{2}}_{s_{1}}\,\frac{m_{0}}{(\sqrt{1\,-\,\frac{v^{2}}{c^{2}}})^{3}}\,\frac{dv}{dt}\,ds\, )
Substituieren der Grenzen und Ausklammern von  : :
^{3}}\,dv )
ähmmm... ... ja genau: ... ja genau:
Lösung des Integrals nach Partieller Integration (würde den Rahmen sprengen, deshlab schreib ich sie einfach hin, wer sie sehen will, dem schick ich sie):

Da sich die relativistische Gesamtenergie aus der kinetischen und potentiellen Energie/Ruheenergie zusammensetzt, gilt:


Mein erstes LaTeX-Werk, hab dafür jetzt gute 2 Stunden gebraucht. Naja egal, als Abiturient hat man ja Zeit für sowas. Wenn jemand Lust hat, das nachschaut und Fehler findet, bitte posten.
Sagt mal, wo bekomm ich denn LaTex her? Ist das Freeware? Ich brauch das unbedingt... |
|
 |
Gast
|
 Gast Verfasst am: 07. Jul 2004 18:32 Titel: Naja... Gast Verfasst am: 07. Jul 2004 18:32 Titel: Naja... |
 |
|
Vielen Dank dass du den umgestellt hast @Thomas 
Hab mal ne Frage, wie wärs wenn du eine die neue Kategorie Relativistische Physik aufmachen würdest? Es gibt nämlich soviele Beiträge, die eher da rein passen würden. Gut, ich weiß, ist nicht grade Schulphysik... aber wie wär das?
Gruß
Neko |
|
 |
Gast
|
 Gast Verfasst am: 07. Jul 2004 19:28 Titel: Gast Verfasst am: 07. Jul 2004 19:28 Titel: |
 |
|
|
Was ich bei der "Herleitung" nicht verstehe, ist wo das m(v) herkommt. Das beinhaltet schon die Energie/Masse Equivalenz die man herleiten will.. |
|
 |
Gast
|
 Gast Verfasst am: 07. Jul 2004 22:56 Titel: Gast Verfasst am: 07. Jul 2004 22:56 Titel: |
 |
|
Respekt! Da hast du dir ja wirklich Mühe gegeben - und das als Abiturient. 
Soweit ich das beurteilen kann, gibts da nichts auszusetzen (außer dass Ekin mit Ziffer 4 deklariert werden müsste, aber über solche Bagatellen wollen wir ja nicht reden  ) )
Gruß
Philipp |
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 08. Jul 2004 15:11 Titel: Neko Verfasst am: 08. Jul 2004 15:11 Titel: |
 |
|
| Anonymous hat Folgendes geschrieben: | | Was ich bei der "Herleitung" nicht verstehe, ist wo das m(v) herkommt. Das beinhaltet schon die Energie/Masse Equivalenz die man herleiten will.. |
Das
\,=\,\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^2}}})
ist die transformierte Masse. Sie beinhaltet, dass sich lediglich die Masse ändert, wenn 
In der Formel ist kein E drin. Soll ich dir die Masse auch trotzdem noch transformieren? *seufz* 
Gruß Neko |
|
 |
Gast
|
 Gast Verfasst am: 08. Jul 2004 15:46 Titel: Gast Verfasst am: 08. Jul 2004 15:46 Titel: |
 |
|
|
Was heist lediglich? Das ist doch der Witz dabei, diese Formel beinhaltet die Energie-Masse Äquivalenz. Wenn man annimmt, das diese Formel richtig ist, kann man auch gleich E=mc² annehmen.. |
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 08. Jul 2004 16:45 Titel: Neko Verfasst am: 08. Jul 2004 16:45 Titel: |
 |
|
Man könnte auf den Gedanken kommen, das ist richtig, bei
\,=\,\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^2}}})
Kannst du aber bloß erkennen, dass bei größer werdendem v der Bruch  gegen 1 geht, somit der Nenner aus gegen 1 geht, somit der Nenner aus  gegen null geht, und damit der ganze Ausdruck gegen null geht, und damit der ganze Ausdruck  immer größer wird, immer größer wird, ) somit mit somit mit  steigt. steigt.
Zu dieser Formel gelangt man auch ganz einfach aus logischem Schlussfolgern. Beispiel: In einem Radialbeschleuniger werden mit hilfe von magnetischen Feldern Teilchen auf einen (ich drücks jetzt mal so aus) "nennenswerten" Bruchteil der Lichtgeschwindigkeit beschleunigt. Die Geschwindigkeit, die sie dann erreichen, lässt sich mit dem beinahe klassischsten Ansatz der Physik errechnen. Wenn die Beschleunigungsspannun U anliegt, die Teilchen die Masse m und die Ladung q besitzen, haben sie die Geschwindigkeit (Nach EES-Ansatz):

bei einer Beschleunigungsspannung von  wäre die Geschwindigkeit schon wäre die Geschwindigkeit schon  was die Lichtgeschwindigkeit übersteigt! was die Lichtgeschwindigkeit übersteigt!
Zwingend muss die bewegte Masse also größer sein, als die Ruhemasse. Man muss also einfach die Ruhemasse mit  multiplizieren! Wenn man das dann hergeleitet hat, kann man es für die Herleitung von multiplizieren! Wenn man das dann hergeleitet hat, kann man es für die Herleitung von  ohne Bedenken benutzen! ohne Bedenken benutzen!
Noch was: Die Formel der Massentransformation sagt noch nichts direktes über die Energie aus, man kann es höchstens annehmen, dass bei größer werdendem "m" E auch größer wird. Was du aber noch nicht daran siehst, ist, dass Energie und Masse ja geradezu miteinander ersetzbar sind, dass also Energie zu Masse werden kann und Masse auch zu Energie!
Gruß
Neko  |
|
 |
Thomas
Administrator
Anmeldungsdatum: 20.02.2004
Beiträge: 701
|
 Thomas Verfasst am: 08. Jul 2004 17:54 Titel: Thomas Verfasst am: 08. Jul 2004 17:54 Titel: |
 |
|
|
Gehört Relativistische Physik nicht irgendwie zur Quantenphysik dazu? |
|
 |
Gast
|
 Gast Verfasst am: 08. Jul 2004 18:20 Titel: Gast Verfasst am: 08. Jul 2004 18:20 Titel: |
 |
|
Weiß nicht, ist aber auch egal. Relativistische Physik ist doch ein irre großes Thema! Was man da alles reinpacken kann: Minkowski-Diagramme, Lorentz-Transformationen, Optischer Doppler-Effekt, die Einstein-Postulate...*schwärm* Außrdem wirds in diesem Physik Zweig demnächst nochmal spannend, wenn die hier im Forum vielfach erwähnte Gravity Probe B Sonde die Theorien EInsteins überprüft...
Gruß
Neko  |
|
 |
Naemi
Moderator
Anmeldungsdatum: 01.06.2004
Beiträge: 497
Wohnort: Bonn
|
 Naemi Verfasst am: 08. Jul 2004 18:40 Titel: Naemi Verfasst am: 08. Jul 2004 18:40 Titel: |
 |
|
Im Normalfall wird die relativistische Physik zur Mechanik gezählt -- ist ja erstmal eine Erweiterung dieser.
Grüße 
Naemi |
|
 |
navajo
Moderator

Anmeldungsdatum: 12.03.2004
Beiträge: 618
Wohnort: Bielefeld
|
 navajo Verfasst am: 09. Jul 2004 12:06 Titel: navajo Verfasst am: 09. Jul 2004 12:06 Titel: |
 |
|
Hmpf ich häng schon bei der ersten Zeile fest 
| Neko hat Folgendes geschrieben: | \,=\,\frac{dm}{dt}\,v\,+\,\frac{dv}{dt}\,m\,=\,\frac{dm}{dt}\,v\,+\,m\,\cdot\,a\,=\,\frac{dm}{dt}\,v\,+\,m\,\cdot\,a\,=\,\frac{dv}{dt}\,(\,\frac{dm}{dt}\,v\,)\,+\,m\,\cdot\,a\,=\,\frac{dv}{dt}\,\frac{dm}{dv}\,v\,+\,m\,\cdot\,a\,=\,a\,(\frac{dm}{dv}\,v\,+\,m\,))
(1) |
Wo kommt beim 6ten Gleichheitszeichen das  her? also ich meine das hier: her? also ich meine das hier:
\,+\,m\,\cdot\,a\,)
Hmm naja das wollt ich auch nur wissen, von selbst komm ich irgentwie nicht drauf  |
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 09. Jul 2004 14:34 Titel: Neko Verfasst am: 09. Jul 2004 14:34 Titel: |
 |
|
Wow, gut gesehen. Respekt! 
Da hab ich mich vertippt. Es muss natürlich
\,+\,m\,\cdot\,a\,)
heißen. Außerdem hab ich eine Umformung doppelt hingeschrieben. Naja kann passieren
Gruß
Neko 
[Ich habe das auch oben in der ursprünglichen Formel dementsprechend korrigiert, dann wird das lesbarer. Gruß, dermarkus] |
|
 |
navajo
Moderator

Anmeldungsdatum: 12.03.2004
Beiträge: 618
Wohnort: Bielefeld
|
 navajo Verfasst am: 09. Jul 2004 14:47 Titel: navajo Verfasst am: 09. Jul 2004 14:47 Titel: |
 |
|
Ah achso 
Hmm, wenn ich mir den nächsten Schritt genauer angeguckt hätte, hätt man auch drauf kommen können, da isses ja wieder richtig  |
|
 |
mr. black
Moderator

Anmeldungsdatum: 04.07.2004
Beiträge: 228
Wohnort: Krumbach/Österreich
|
 mr. black Verfasst am: 09. Jul 2004 16:14 Titel: mr. black Verfasst am: 09. Jul 2004 16:14 Titel: |
 |
|
Hallo alle zusammen.
In der Schule haben wir nie die Notationsweise:
d/dt(m*v)
ist das 'd' das Zeichen für "Delta"
oder hab ich da was verpasst. Hab diese Notationsweise noch
nie gesehen.

_________________
You just have to push the right key with the right finger at the right time then the organ makes the sound without effort
J.S. Bach |
|
 |
mr. black
Moderator

Anmeldungsdatum: 04.07.2004
Beiträge: 228
Wohnort: Krumbach/Österreich
|
 mr. black Verfasst am: 09. Jul 2004 16:18 Titel: mr. black Verfasst am: 09. Jul 2004 16:18 Titel: |
 |
|
entschuldigung hab ein paar worte vergessen
wollte nur sagen, dass ich das noch nicht gesehen habe
in der Schule.
_________________
You just have to push the right key with the right finger at the right time then the organ makes the sound without effort
J.S. Bach |
|
 |
Naemi
Moderator
Anmeldungsdatum: 01.06.2004
Beiträge: 497
Wohnort: Bonn
|
 Naemi Verfasst am: 09. Jul 2004 16:23 Titel: Naemi Verfasst am: 09. Jul 2004 16:23 Titel: |
 |
|
Das d ist ein/das Zeichen für die Ableitung. Wenn man das bekannte 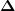 gegen Null laufen lässt, hat man die Ableitung. Diese wird mit d bezeichnet. gegen Null laufen lässt, hat man die Ableitung. Diese wird mit d bezeichnet.
Besser vorstellbar ist es mit einem Graphen: Wenn mit 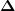 die Steigung einer Sekante berechnet wird, kann man mit der Ableitung die Steigung in einem Punkt bestimmen (klingt dämlich, habe mich auch erst daran gewöhnt, als ich es benutzen musste die Steigung einer Sekante berechnet wird, kann man mit der Ableitung die Steigung in einem Punkt bestimmen (klingt dämlich, habe mich auch erst daran gewöhnt, als ich es benutzen musste  ) )
Klarer?
Grüße
Naemi |
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 11. Jul 2004 00:30 Titel: Neko Verfasst am: 11. Jul 2004 00:30 Titel: |
 |
|
Genau. Für

kannst du auch schreiben:
 (In der Physik sehr geläufig, obwohl man hier nicht erkennt nach was abgeleitet wird- so sind die Physiker eben (In der Physik sehr geläufig, obwohl man hier nicht erkennt nach was abgeleitet wird- so sind die Physiker eben  ) )
Oder (und das wird dir jetzt wieder bekannt vorkommen):
) |
|
 |
Naemi
Moderator
Anmeldungsdatum: 01.06.2004
Beiträge: 497
Wohnort: Bonn
|
 Naemi Verfasst am: 11. Jul 2004 02:26 Titel: Naemi Verfasst am: 11. Jul 2004 02:26 Titel: |
 |
|
Das mit dem Punkt stimmt nicht ganz: Er ist zwar sehr geläufig, kennzeichnet jedoch nur die Ableitung(en) nach der Zeit.
Für Ableitungen nach x, y, z, r und dergleichen kommt nur der  in Frage.... in Frage....
Grüße 
Naemi |
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 11. Jul 2004 03:08 Titel: Neko Verfasst am: 11. Jul 2004 03:08 Titel: |
 |
|
Wieder was dazu gelernt. Danke große Naemi 
Gruß
Neko |
|
 |
BlackJack

Anmeldungsdatum: 07.03.2004
Beiträge: 89
Wohnort: org 100h / Münsterland
|
 BlackJack Verfasst am: 11. Jul 2004 03:29 Titel: BlackJack Verfasst am: 11. Jul 2004 03:29 Titel: |
 |
|
hmm, also meiner meinung nach dürfte das hier:
^{-3}}\,=\,m_{0}\,\cdot\,\frac{v}{c^{2}}\sqrt{\gamma^{3}})
nur sinn ergeben, wenn das hoch drei im letzten schritt sich auf die gesamte wurzel und nicht nur auf das gamma unter der wurzel beziehen würde, oder?
ach ja, und den zweiten schritt in der ersten zeile (da wo beim auflösen der klammer plötzlich eine summe auftaucht) verstehe ich auch nicht so recht, könnte mir das jemand erklären?
danke.
edit:
ups, ich sehe gerade, das ist einfach nur die kettenregel, oder?
_________________
Auf ein gefettetes Backblech legen und bei zweihundert Grad für fünfzehn Minuten backen und KEINE EIER
Tool, Die Eier von Satan
Fraktal3D |
|
 |
mr. black
Moderator

Anmeldungsdatum: 04.07.2004
Beiträge: 228
Wohnort: Krumbach/Österreich
|
 mr. black Verfasst am: 11. Jul 2004 15:24 Titel: mr. black Verfasst am: 11. Jul 2004 15:24 Titel: |
 |
|
dieses d ist dumm
_________________
You just have to push the right key with the right finger at the right time then the organ makes the sound without effort
J.S. Bach |
|
 |
navajo
Moderator

Anmeldungsdatum: 12.03.2004
Beiträge: 618
Wohnort: Bielefeld
|
 navajo Verfasst am: 11. Jul 2004 15:52 Titel: navajo Verfasst am: 11. Jul 2004 15:52 Titel: |
 |
|
| BlackJack hat Folgendes geschrieben: | hmm, also meiner meinung nach dürfte das hier:
^{-3}}\,=\,m_{0}\,\cdot\,\frac{v}{c^{2}}\sqrt{\gamma^{3}})
nur sinn ergeben, wenn das hoch drei im letzten schritt sich auf die gesamte wurzel und nicht nur auf das gamma unter der wurzel beziehen würde, oder?
|
 ist doch definiert als: ist doch definiert als:  wen ich mich nicht irre. Dann müsste imo die Wurzel einfach ganz weg, sondern einfach nur wen ich mich nicht irre. Dann müsste imo die Wurzel einfach ganz weg, sondern einfach nur  . In der Zeil dadrunter verschwindet die Wurzel ja auch plötzlich wieder. Ich tippe auf nen Tippfehler . In der Zeil dadrunter verschwindet die Wurzel ja auch plötzlich wieder. Ich tippe auf nen Tippfehler 
_________________
Das Universum ist 4 Mio Jahre alt, unbewohnt und kreist um die Sonne. |
|
 |
Naemi
Moderator
Anmeldungsdatum: 01.06.2004
Beiträge: 497
Wohnort: Bonn
|
 Naemi Verfasst am: 11. Jul 2004 17:29 Titel: Naemi Verfasst am: 11. Jul 2004 17:29 Titel: |
 |
|
| mr. black hat Folgendes geschrieben: | | dieses d ist dumm |
Meinst du blöd oder dumm? Weil es im Prinzip ziemlich praktisch ist, aber blöde finden kannst du es ruhig.
Aprops: Eine zweite Ableitung wird durch  dargestellt -- es hat einige Zeit gedauert, bis ich wusste, wohin die Zwei kommt dargestellt -- es hat einige Zeit gedauert, bis ich wusste, wohin die Zwei kommt 
@Thomas: Wo bleibt der mimetex-Knopf 
Grüße
Naemi |
|
 |
Mathespezialschüler
Anmeldungsdatum: 14.05.2004
Beiträge: 22
Wohnort: Berlin
|
 Mathespezialschüler Verfasst am: 11. Jul 2004 23:19 Titel: Mathespezialschüler Verfasst am: 11. Jul 2004 23:19 Titel: |
 |
|
| BlackJack hat Folgendes geschrieben: | hmm, also meiner meinung nach dürfte das hier:
^{-3}}\,=\,m_{0}\,\cdot\,\frac{v}{c^{2}}\sqrt{\gamma^{3}})
nur sinn ergeben, wenn das hoch drei im letzten schritt sich auf die gesamte wurzel und nicht nur auf das gamma unter der wurzel beziehen würde, oder? |
Hi, ich wollt nur mal schnell aufklären, falls ich das Problem richtig verstanden habe (auch wenn die Wurzel weg müssen sollte, wie navajo geschrieben hat, wo ich auch zustimme, wenn  so definiert ist): so definiert ist):
^3 = \sqrt{\gamma^3})
Und noch folgendes: Wenn  wirklich so definiert ist: wirklich so definiert ist:
| navajo hat Folgendes geschrieben: |
 ist doch definiert als: ist doch definiert als:  |
, dann ist doch ^{-3}}}\ =\ \frac{1}{\frac{1}{(\sqrt{1-\frac{v^2}{c^2})^3}}}\ =\ \frac{1}{\gamma^3}\ =\ \gamma^{-3})
 |
|
 |
navajo
Moderator

Anmeldungsdatum: 12.03.2004
Beiträge: 618
Wohnort: Bielefeld
|
 navajo Verfasst am: 11. Jul 2004 23:54 Titel: navajo Verfasst am: 11. Jul 2004 23:54 Titel: |
 |
|
Das  so definiert ist müsste stimmen, habs grad nochmal nachgeschaut. so definiert ist müsste stimmen, habs grad nochmal nachgeschaut.
| Mathespezialschüler hat Folgendes geschrieben: |
, dann ist doch ^{-3}}}\ =\ \frac{1}{\frac{1}{(\sqrt{1-\frac{v^2}{c^2})^3}}}\ =\ \frac{1}{\gamma^3}\ =\ \gamma^{-3})
|
Hmmm stimmt ja auch, jetzt bin ich ganz verwirrt 
_________________
Das Universum ist 4 Mio Jahre alt, unbewohnt und kreist um die Sonne. |
|
 |
mr. black
Moderator

Anmeldungsdatum: 04.07.2004
Beiträge: 228
Wohnort: Krumbach/Österreich
|
 mr. black Verfasst am: 12. Jul 2004 10:26 Titel: mr. black Verfasst am: 12. Jul 2004 10:26 Titel: |
 |
|
ich glaub jetzt weis ich was das 'd' wirklich bedeutet:
Die Zeitverzerrung ist bei einem relativ beschleunigtem System ist ja
das Integral aus dt(1-v(t)²/c²).
dann müsste ja als Beispiel der zurückgelegte weg in der Klassischen
Mechanik bei einem gleichm beschl System
Integral (dt(a*t))=a*t²/2 sein oder   
oder oder ??   ´ ´
das 'd' ist also unendlich klein aber nicht 0 
_________________
You just have to push the right key with the right finger at the right time then the organ makes the sound without effort
J.S. Bach |
|
 |
mr. black
Moderator

Anmeldungsdatum: 04.07.2004
Beiträge: 228
Wohnort: Krumbach/Österreich
|
 mr. black Verfasst am: 12. Jul 2004 10:30 Titel: mr. black Verfasst am: 12. Jul 2004 10:30 Titel: |
 |
|
entschuldigung ich meine natürlich 1/sqrt(1-v(t)²/c²)
tut mir leid   

edit: geht doch danke   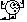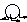
_________________
You just have to push the right key with the right finger at the right time then the organ makes the sound without effort
J.S. Bach
Zuletzt bearbeitet von mr. black am 12. Jul 2004 20:42, insgesamt einmal bearbeitet |
|
 |
navajo
Moderator

Anmeldungsdatum: 12.03.2004
Beiträge: 618
Wohnort: Bielefeld
|
 navajo Verfasst am: 12. Jul 2004 16:16 Titel: navajo Verfasst am: 12. Jul 2004 16:16 Titel: |
 |
|
Ich glaub die Ableitung ist falsch, also das minus bei der hoch 3 ist zuviel. meiner meinung nach kommt sowas raus:
^{-\frac{1}{2}}\right)= -\frac{1}{2}m_0(1-\frac{v^2}{c^2})^{-\frac{3}{2}}\cdot-\frac{2v}{c^2}=m_0\frac{v}{c^2}\sqrt{1-\frac{v^2}{c^2} }^{-3}=m_0\frac{v}{c^2}\gamma^3)
Und damit hat er dann ja letzendlich auch weitergerechnet. Mal sehen ob ich auch noch hinkriege wie er bei den Haupnenner bilden da ein  rausbaut. Das hab ich auch noch nicht raus rausbaut. Das hab ich auch noch nicht raus 
EDIT: Oh ist ja garnicht so schwer muss man ja echt nur Hauptnenner bilden  aber ist das richtig so wie dass da steht? müssen über die beiden Wurzeln nicht noch Potenzen? aber ist das richtig so wie dass da steht? müssen über die beiden Wurzeln nicht noch Potenzen?
_________________
Das Universum ist 4 Mio Jahre alt, unbewohnt und kreist um die Sonne. |
|
 |
Naemi
Moderator
Anmeldungsdatum: 01.06.2004
Beiträge: 497
Wohnort: Bonn
|
 Naemi Verfasst am: 12. Jul 2004 17:12 Titel: Naemi Verfasst am: 12. Jul 2004 17:12 Titel: |
 |
|
| mr. black hat Folgendes geschrieben: | | das 'd' ist also unendlich klein aber nicht 0 |
Stimmt im Prinzip.
d bezeichnet somit einen Grenzwertprozess, wo die Differenz immer kleienr und am Ende aber eigentlich null wird... 
Wenn man also sagt Unendlich klein wird irgendwann zu null hat man´s.
Grüße
Naemi |
|
 |
Thomas
Administrator
Anmeldungsdatum: 20.02.2004
Beiträge: 701
|
 Thomas Verfasst am: 12. Jul 2004 17:35 Titel: Thomas Verfasst am: 12. Jul 2004 17:35 Titel: |
 |
|
| mr. black hat Folgendes geschrieben: | entschuldigung ich meine natürlich 1/sqrt(1-v(t)²/c²)
tut mir leid   
 |
Über deinem "falschen" Beitrag müsste sich ein Button "Edit" befinden, mit dem du deinen Fehler direkt berichtigen kannst 
Gruß,
Thomas |
|
 |
Meromorpher

Anmeldungsdatum: 09.03.2004
Beiträge: 388
|
 Meromorpher Verfasst am: 12. Jul 2004 17:43 Titel: Meromorpher Verfasst am: 12. Jul 2004 17:43 Titel: |
 |
|
@Naemi: Das ist von der Bedeutung korrekt, aber von der Definition etwas anders:
'd' bezeichnet ein Differential. Ein D. einer unabhängigen Variable x ist ein beliebiger Zuwachs der Größe x gemäß  . (Bronstein) Das Differential einer Funktion y=f(x) einer Veränderlichen x ist . (Bronstein) Das Differential einer Funktion y=f(x) einer Veränderlichen x ist dx) . f' ist der Differentialquotionent. Dann ist . f' ist der Differentialquotionent. Dann ist  . . |
|
 |
mr. black
Moderator

Anmeldungsdatum: 04.07.2004
Beiträge: 228
Wohnort: Krumbach/Österreich
|
 mr. black Verfasst am: 12. Jul 2004 20:51 Titel: mr. black Verfasst am: 12. Jul 2004 20:51 Titel: |
 |
|
Danke für die Erklärungen ich habs glaub ich verstanden
aber aus euren Erklärungen werd ich nicht sehr viel schlauer.
Ihr formuliert so komplizierte Sätze.
 
Bitte nochmal eine Vollständige Definition der Differentialrechnung oder
wie das heißt
   
_________________
You just have to push the right key with the right finger at the right time then the organ makes the sound without effort
J.S. Bach |
|
 |
Naemi
Moderator
Anmeldungsdatum: 01.06.2004
Beiträge: 497
Wohnort: Bonn
|
 Naemi Verfasst am: 12. Jul 2004 21:13 Titel: Naemi Verfasst am: 12. Jul 2004 21:13 Titel: |
 |
|
Hab´s mal bei Wikipedia eingegeben:
| Zitat: | | In der Mathematik kann mit dem Differential die Steigung einer Funktion an einer bestimmten Stelle berechnet werden. Das Problem, die Steigung zu ermitteln, tritt an vielen Stellen auf, etwa, wenn eine Tangente an eine Kurve angelegt werden soll oder in der Physik bei der Bestimmung der momentanen Geschwindigkeit. |
Sag ich´s doch 
| Zitat: | Man kann die Steigung an der Stelle 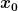 wie folgt berechnen: wie folgt berechnen:
=\frac{f(x) - f(x_0)}{x - x_0}) |
Das wäre die Sekantensteigung. Um auf die gesuchte Tangentensteigung zu kommen, wird der Grenzwert (limes) bestimmt:
 = f´(x) = \frac{df}{dx} = \lim_{x_0\to 0} \frac{f(x) - f(x_0)}{x - x_0})
Die Steigung im kartesischen Koordinatensystem wird ja mit 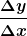 berechnet... berechnet...
Grüße
Naemi
p.s.: Das da oben mit dem Unendlich ist grosser Müll  |
|
 |
Mathespezialschüler
Anmeldungsdatum: 14.05.2004
Beiträge: 22
Wohnort: Berlin
|
 Mathespezialschüler Verfasst am: 12. Jul 2004 21:45 Titel: Mathespezialschüler Verfasst am: 12. Jul 2004 21:45 Titel: |
 |
|
| Naemi hat Folgendes geschrieben: | Hab´s mal bei Wikipedia eingegeben:
| Zitat: | Man kann die Steigung an der Stelle 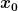 wie folgt berechnen: wie folgt berechnen:
=\frac{f(x) - f(x_0)}{x - x_0}) |
...
p.s.: Das da oben mit dem Unendlich ist grosser Müll  |
Müsstest du nicht korrekterweise sagen
=\lim_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}) ??? ???
Und was meinst du mit dem Müll??
edit: Nochmal was dazu: Du hast geschrieben/zitiert | Zitat: | Man kann die Steigung an der Stelle 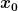 wie folgt berechnen: wie folgt berechnen:
=\frac{f(x) - f(x_0)}{x - x_0}) |
Wenn du die Steigung der Tangente, also die Ableitung im Punkt x_0 bestimmen willst, läuft das wie oben erklärt. Wenn du die Sekantensteigung (m) der Sekante, die durch x und x_0 geht, bestimmen willst, dann müsstest du schreiben:
 - f(x_0)}{x - x_0})
Da darf man nicht f'(x) schreiben, da f'(x) definiert ist als Steigung der Tangente, also mit dem grenzwert wie oben. Das hat relativ wenig mit der Sekantensteigung zu tun. |
|
 |
Naemi
Moderator
Anmeldungsdatum: 01.06.2004
Beiträge: 497
Wohnort: Bonn
|
 Naemi Verfasst am: 13. Jul 2004 00:26 Titel: Naemi Verfasst am: 13. Jul 2004 00:26 Titel: |
 |
|
Also:
Das erste war ein Zitat von Wikipedia. Hast natürlich recht mit dem fehlenden Limes.
Der Müll war auf eine andere Stelle bezogen:
| ich hat Folgendes geschrieben: |
d bezeichnet somit einen Grenzwertprozess, wo die Differenz immer kleienr und am Ende aber eigentlich null wird...  |
Das Unendlich hat da natürlich überhaupt nichts zu suchen...
Allerdings kann man m auch als Tangentensteigung beschreiben, nicht nur als Sekantensteigung (je nach Bedarf, hier war die Tangente gemeint  ) )
Schlaft gut 
Naemi |
|
 |
Mathespezialschüler
Anmeldungsdatum: 14.05.2004
Beiträge: 22
Wohnort: Berlin
|
 Mathespezialschüler Verfasst am: 13. Jul 2004 15:49 Titel: Mathespezialschüler Verfasst am: 13. Jul 2004 15:49 Titel: |
 |
|
| Naemi hat Folgendes geschrieben: | Also:
Allerdings kann man m auch als Tangentensteigung beschreiben, nicht nur als Sekantensteigung (je nach Bedarf, hier war die Tangente gemeint  ) )
Schlaft gut 
Naemi |
Ja kannst die Tangentensteigung natürlich auch mit m bezeichnen, nur darfst du nicht die Sekantensteigung mit f'(x) bezeichnen, aber ich denk, das is ja jetz klar. |
|
 |
mr. black
Moderator

Anmeldungsdatum: 04.07.2004
Beiträge: 228
Wohnort: Krumbach/Österreich
|
 mr. black Verfasst am: 13. Jul 2004 20:52 Titel: mr. black Verfasst am: 13. Jul 2004 20:52 Titel: |
 |
|
jetzt is ma alles klar mit dem 'd'
Das was ihr da besprochen habt kommt schon linearer Interpolation nahe
bzw. das ist es im Grunde!
danke!!! 
_________________
You just have to push the right key with the right finger at the right time then the organ makes the sound without effort
J.S. Bach |
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 17. Jul 2004 00:53 Titel: Neko Verfasst am: 17. Jul 2004 00:53 Titel: |
 |
|
au backe, soviel mathe. Das ist ein Physikerboard, ja!  Der Physiker merkt sich: Eine nach einer bestimmten Varibale veränderliche Größe wird durch die Ableitung ausgedrückt. Solässt sich die sich in einem Zeitintervall verändernde Geschwindigkeit mit der Beschleunigung ausdrücken. Basta. Der Physiker merkt sich: Eine nach einer bestimmten Varibale veränderliche Größe wird durch die Ableitung ausgedrückt. Solässt sich die sich in einem Zeitintervall verändernde Geschwindigkeit mit der Beschleunigung ausdrücken. Basta.
(sind aber alles basics, lernt man eigentlich in Klasse 11 schon  ) )
Gruß
Neko |
|
 |
Mathespezialschüler
Anmeldungsdatum: 14.05.2004
Beiträge: 22
Wohnort: Berlin
|
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 17. Jul 2004 13:20 Titel: Nikolas Verfasst am: 17. Jul 2004 13:20 Titel: |
 |
|
Du bist noch nicht in der 11??? Und gehst so heftig in Mathe ab? Repekt 
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
|
















 ... ja genau:
... ja genau:

 )
)









 Der Physiker merkt sich: Eine nach einer bestimmten Varibale veränderliche Größe wird durch die Ableitung ausgedrückt. Solässt sich die sich in einem Zeitintervall verändernde Geschwindigkeit mit der Beschleunigung ausdrücken. Basta.
Der Physiker merkt sich: Eine nach einer bestimmten Varibale veränderliche Größe wird durch die Ableitung ausgedrückt. Solässt sich die sich in einem Zeitintervall verändernde Geschwindigkeit mit der Beschleunigung ausdrücken. Basta.