| Autor |
Nachricht |
Guevara2
Anmeldungsdatum: 28.06.2004
Beiträge: 14
|
 Guevara2 Verfasst am: 12. Jul 2004 12:37 Titel: Aufladung und Entladung eines Kondensators Guevara2 Verfasst am: 12. Jul 2004 12:37 Titel: Aufladung und Entladung eines Kondensators |
 |
|
Ein Kondensator entläd sich an einem Widerstand.Bei einem Kondensator ist die Spannung proportional zur Ladung. Deshalb ist der Strom der Entladung proportional zu Ladung. Daher komme ich auf die Gleichung  . Es kann nur . Es kann nur }) sein. Darum muss ich um auf a zu kommen den Strom zum Zeitpunkt 0 berechen. sein. Darum muss ich um auf a zu kommen den Strom zum Zeitpunkt 0 berechen.
R=1K Ohm
Der Kondensator hat C= 1mF miteiner Ladung von Q=10mc.
Demnach ist 
Demnach ist 
Also =y=10mc*e^{(-t)})
 =y' =-10mA*e^{(-t)})
Hab ich das richtig gemacht?
|
|
 |
Mathespezialschüler
Anmeldungsdatum: 14.05.2004
Beiträge: 22
Wohnort: Berlin
|
 Mathespezialschüler Verfasst am: 12. Jul 2004 12:47 Titel: Mathespezialschüler Verfasst am: 12. Jul 2004 12:47 Titel: |
 |
|
Den gleichen Thread in Mathe- und Physikerboard zu erstellen, ist aber nicht grad sehr nett.  
|
|
 |
Guevara2
Anmeldungsdatum: 28.06.2004
Beiträge: 14
|
 Guevara2 Verfasst am: 12. Jul 2004 13:34 Titel: Guevara2 Verfasst am: 12. Jul 2004 13:34 Titel: |
 |
|
|
Ich konnte mich nicht entscheiden wohin es eher passt. ich hoffe es stört nicht sonderlich.
|
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 17. Jul 2004 01:04 Titel: Neko Verfasst am: 17. Jul 2004 01:04 Titel: |
 |
|
Hab da mal drüber geschaut. Ist schon 1 Uhr nachts, und so wie ich das seh seiht das richtig aus. Schua aber morgen noch mal drüber. Der Ansatz bei der Differentialgleichung ist goldrichtig. Wo hast du genau noch ein Problem? Wenn du willst, kann ich dir mal die Herleitung des Spannungsverlaufes (Sowohl beim Lade- als auch Entladevorgang) hier posten.*seufz, das wird wieder ein stück arbeit. Aber ich machs ja gern für euch 
Gruß
Neko 
|
|
 |
Teufelus
Anmeldungsdatum: 11.04.2004
Beiträge: 62
Wohnort: Hannover
|
 Teufelus Verfasst am: 18. Jul 2004 04:06 Titel: Teufelus Verfasst am: 18. Jul 2004 04:06 Titel: |
 |
|
hmm. Fast richtig. Nur taucht die Zeitkonstante T für den Kondensator nicht in deiner Formel auf. Die allgemeingültige Formel lautet: i(t) = - Imax * e^(-t/T). Dabei ist T = R*C.
Für T kann man sich merken, dass der Kondensator nach ca. 5 * T aufgeladen bzw. entladen ist.
|
|
 |
Teufelus
Anmeldungsdatum: 11.04.2004
Beiträge: 62
Wohnort: Hannover
|
 Teufelus Verfasst am: 19. Jul 2004 22:21 Titel: Aufladung und Entladung eines Kondensators Teufelus Verfasst am: 19. Jul 2004 22:21 Titel: Aufladung und Entladung eines Kondensators |
 |
|
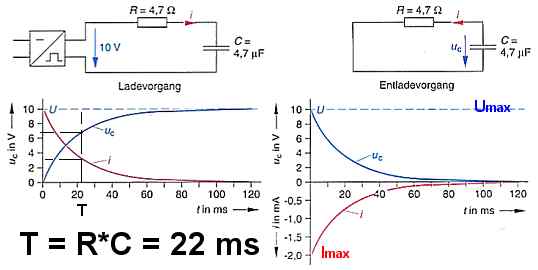
So, der Vollständigkeithalber habe den Beitrag mal in Auf - / Entladung eines Kondensators umbenannt! Habe zudem zwei Diagramme angehängt, an denen man den Vorgang deutlich erkennen kann.
zusammenfassend...
Für die Aufladung gilt:
nach t = T: uc = 63 % Umax, ic = 37 % Imax
nach t = 5T: uc = Umax, ic = 0 A <-- Kondensator ist aufgeladen!
Für die Entladung gilt:
nach t = 5T: uc =0 V, ic = 0 A <-- Kondensator ist entladen!
| Beschreibung: |
|
| Dateigröße: |
15.27 KB |
| Angeschaut: |
115957 mal |
|
|
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 24. Jul 2004 16:43 Titel: Neko Verfasst am: 24. Jul 2004 16:43 Titel: |
 |
|
Gleich gibts die komplette herleitung. haltet aus! 
|
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 24. Jul 2004 17:55 Titel: Herleitung Neko Verfasst am: 24. Jul 2004 17:55 Titel: Herleitung |
 |
|
So habs fertig. Hier die Herleitung des Spannungsverlaufes am Kondensator (Auf- und Entladung).
Das Schaltbild ist simpel: Ein Kondesator mit der Kapazität 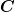 wird mit einem elektrischen Widerstand wird mit einem elektrischen Widerstand  in Reihe geschaltet und jeweils die Spannung über dem Kondensator in Reihe geschaltet und jeweils die Spannung über dem Kondensator  und dem Widerstand und dem Widerstand  gemessen. In dem Schaltkreis befindet sich außerdem noch eine Stromquelle, die beim Betätigen eines Schalters die Spannung gemessen. In dem Schaltkreis befindet sich außerdem noch eine Stromquelle, die beim Betätigen eines Schalters die Spannung 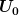 liefert liefert
Die Quellenspannung 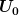 liefert die Spannungen am Kondensator und am Widerstand. Es gilt: liefert die Spannungen am Kondensator und am Widerstand. Es gilt:
 (1) (1) 
(mit }{C}) und und \,=\,R\,\cdot\,\dot{Q}(t)) ) )
}{C}\,+\,\,R\,\cdot\,\dot{Q}(t)) (2) (2)
Durch  teilen: teilen:
\,+\,\dot{Q}(t)) (3) (3)  (lineare inhomogene Differentialgleichung erster Ordnung) (lineare inhomogene Differentialgleichung erster Ordnung)
Aus Gründen der Einfachheit fang ich mit der Entladung an...
a) Entladung (Schalter geöffnet, kein Quellenstrom)
Die Differentialgleichung bei (3) wird nun mit den folgenden Angaben gelöst:
zum Zeitpunkt  gilt: gilt: =Q_{0}) und und =U_{0})
\,+\,\frac{1}{RC}\,Q(t)\,=\,0)
Durch ) teilen und das teilen und das \,) auf die ander Seite auf die ander Seite
}{Q(t)}\,=\,-\,\frac{1}{RC})
Beide Seiten Integrieren nach t:
}{Q(t)}\,dt\,=\,-\int\limits_{t_{0}}^{t}\,\frac{1}{RC}dt)
|\,]^{t}_{t_{0}}\,=\,[-\,\frac{1}{RC}]^{t}_{t_{0}})
|\,-\,ln\,|Q(t_{0})|\,=\,-\,\frac{1}{RC}\,\cdot\,t\,-\,\frac{1}{RC}\,\cdot\,t_{0})
}{Q_{0}}|\,=\,-\,\frac{1}{RC}\,(t\,-\,t_{0}))
}{Q_{0}}\,=\,e^{\,-\frac{1}{RC}\,(t\,-\,t_{0})})
\,=\,Q_{0}\cdot\,e^{-\frac{1}{RC}t})  (Ladungsverlauf) (Ladungsverlauf)
mit \,=\,\frac{Q_{c}(t)}{C}) folgt daraus: folgt daraus:
\,=\,U_{0}\,\cdot\,e^{-\frac{1}{RC}t}) (4) (4)
So, denn Aufladevorgang gibts vielleicht noch heut abend. Geh jetzt erst mal schwimmen. 
Gruß
Neko 
Zuletzt bearbeitet von Neko am 02. Nov 2005 19:35, insgesamt 3-mal bearbeitet |
|
 |
daHooligan
Anmeldungsdatum: 25.09.2004
Beiträge: 1
|
 daHooligan Verfasst am: 26. Sep 2004 21:24 Titel: daHooligan Verfasst am: 26. Sep 2004 21:24 Titel: |
 |
|
hmmmm.....
warum integrierst du beide Seiten nach t??
Geschieht das nur, um das Q[Punkt] wegzukriegen, oder hat das auch nen anschaulichen Hintergrund (weil Integral entspricht ja der Fläche unter der Kurve )???   
|
|
 |
Gast
|
 Gast Verfasst am: 17. Okt 2004 21:52 Titel: Gast Verfasst am: 17. Okt 2004 21:52 Titel: |
 |
|
Kann mir jemand ein komplettes Reférat über die entladung schicken bin leider in Zeit not habe es versäumt da ich krank war ist sehr wichtig
Danke schonmal hier meine mail>>>>> [email protected]
|
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 17. Okt 2004 22:26 Titel: Nikolas Verfasst am: 17. Okt 2004 22:26 Titel: |
 |
|
 Vergiss es. Das ist so ziemlich das letzte, was du hier erwarten kannst. Ein komplettes Referat? Falls du krank warst, wirst du es nicht abgeben müssen. Vergiss es. Das ist so ziemlich das letzte, was du hier erwarten kannst. Ein komplettes Referat? Falls du krank warst, wirst du es nicht abgeben müssen.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
GhostOfWar
Anmeldungsdatum: 08.10.2004
Beiträge: 9
|
 GhostOfWar Verfasst am: 22. Okt 2004 01:22 Titel: GhostOfWar Verfasst am: 22. Okt 2004 01:22 Titel: |
 |
|
Hallo...Hab eine kleine Frage...wie kommst du von dieser Formel auf die andere?
}{Q(t)}\,dt\)
\,]^{t}_{t_{0}}\,)
Q'(t)=dQ / dt
dt kürzt sich weg
also ist dQ / Q(t) = ln Q(t) ??
|
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 22. Okt 2004 14:45 Titel: Nikolas Verfasst am: 22. Okt 2004 14:45 Titel: |
 |
|
dt kürzt sich weg??? Ich glaube, du hast da etwas nicht ganz richtig verstanden. dt ist keine Zahl, sondern gibt nur an, nach welcher Variablen du Funktion integriert wird (in diesem Fall t)
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
navajo
Moderator

Anmeldungsdatum: 12.03.2004
Beiträge: 618
Wohnort: Bielefeld
|
 navajo Verfasst am: 22. Okt 2004 16:19 Titel: navajo Verfasst am: 22. Okt 2004 16:19 Titel: |
 |
|
Ach als Physiker darf man auch mal ein dt kürzen: 
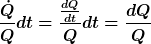
Ansonsten kann man Integrale von diesen Typ mit "Integration durch Substition" lösen. (z.B hier beschrieben: *click*)
_________________
Das Universum ist 4 Mio Jahre alt, unbewohnt und kreist um die Sonne. |
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 02. Feb 2005 11:56 Titel: Neko Verfasst am: 02. Feb 2005 11:56 Titel: |
 |
|
*mal en uralten thread wieder auspack*
| GhostOfWar hat Folgendes geschrieben: | Hallo...Hab eine kleine Frage...wie kommst du von dieser Formel auf die andere?
}{Q(t)}\,dt\)
\,]^{t}_{t_{0}}\,)
Q'(t)=dQ / dt
dt kürzt sich weg
also ist dQ / Q(t) = ln Q(t) ?? |
Nee...viel einfacher. Wenn du das Integral aus einem Bruch bildest, bei dem im Zähler die Ableitung des Nenners steht, ist dies immer der logarithmus Naturalis des Nenners plus eine Konstante. Ich glaube das ist aber klar oder?
Hmm...könnte ich eigentlich die Herleitung mal bei "Tipps und Tricks" reinpacken
|
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 02. Feb 2005 12:07 Titel: Nikolas Verfasst am: 02. Feb 2005 12:07 Titel: |
 |
|
Wenn das in die Tipps und Tricks kommt, sollten aber noch die Integrationsvariablen geändert werden, da 't' hier einmal als obere Grenze aber auch als Ableitungsvariable genutzt wird.
Von der Mathe her müsste man um das Q(t) im ln noch Betragsstriche setzen.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
Neko

Anmeldungsdatum: 04.07.2004
Beiträge: 526
Wohnort: Berlin
|
 Neko Verfasst am: 02. Feb 2005 12:09 Titel: Neko Verfasst am: 02. Feb 2005 12:09 Titel: |
 |
|
hey du bist Physiker, und nich Mathematiker 
Naja außerdem fehlt na noch die Aufladung des Kondensators. Müsste ich dann au noch schreiben
|
|
 |
Krümel
Gast
|
 Krümel Verfasst am: 08. Nov 2005 09:53 Titel: Kondensator Krümel Verfasst am: 08. Nov 2005 09:53 Titel: Kondensator |
 |
|
hallo leute,
ich muss auch ein referat über "auf-und entladung eines kondensators" machen,aber ich weiß nicht wie ihr alle auf diese ganzen formeln kommt!!!
könnt ihr mir bitte helfen und das so genau wie möglich erklären!?
viele leibe grüße und DANKE
euer krümel
|
|
 |
Dieter5858
Moderator

Anmeldungsdatum: 02.08.2004
Beiträge: 696
Wohnort: Hamburg
|
 Dieter5858 Verfasst am: 08. Nov 2005 16:18 Titel: Dieter5858 Verfasst am: 08. Nov 2005 16:18 Titel: |
 |
|
Hiho
Ist etwas viel das jetzt alles mal eben zu schreiben.
sag du lieber was du niocht verstehst.
Weist du wie ein Kondensator funktioniert?
Bist du mit allen elektrischen Größen vertraut?
Formeln alleine sind nicht vielsagen wenn man die einzelnen Komponenten nicht kennt (das kenne ich auch).
Aber sag uns wo deine Probleme sind
|
|
 |
mona
Gast
|
 mona Verfasst am: 09. Nov 2005 20:05 Titel: mona Verfasst am: 09. Nov 2005 20:05 Titel: |
 |
|
hallo dieter,
kannst du mir vielleicht deine e-mail adresse geben oder icq dann könnten wir so reden!!!meine e-mail ist [email protected] und icq ist 203710110
bitte melde dich,schnell
gruß krümel
|
|
 |
nostradamus_8
Anmeldungsdatum: 22.11.2005
Beiträge: 2
Wohnort: Lübeck
|
 nostradamus_8 Verfasst am: 22. Nov 2005 20:42 Titel: Re: Herleitung nostradamus_8 Verfasst am: 22. Nov 2005 20:42 Titel: Re: Herleitung |
 |
|
| Neko hat Folgendes geschrieben: | So
Aus Gründen der Einfachheit fang ich mit der Entladung an...
|
Hab mal ne Frage: WO besteht der unterschied im Ansatz bei der Herleitung von AUflade- und Entladevorgang?!? Denn wenn ich mich nicht irre beginnt man ja beide Male mit der Maschenregel, oder?!?
 Wäre gut wenn mir da einer den UNterschied in den Verfahren aufzeigen könnte. Soll die Formel nämlich in meiner LK Klausur herleiten können und ich komm da immer n bisschen in Tüdel mit den Ansätzen und den ersten Schritten... Wäre gut wenn mir da einer den UNterschied in den Verfahren aufzeigen könnte. Soll die Formel nämlich in meiner LK Klausur herleiten können und ich komm da immer n bisschen in Tüdel mit den Ansätzen und den ersten Schritten... 
|
|
 |
cosypanther
Anmeldungsdatum: 14.11.2009
Beiträge: 4
|
 cosypanther Verfasst am: 14. Nov 2009 14:49 Titel: cosypanther Verfasst am: 14. Nov 2009 14:49 Titel: |
 |
|
| daHooligan hat Folgendes geschrieben: | hmmmm.....
warum integrierst du beide Seiten nach t??
Geschieht das nur, um das Q[Punkt] wegzukriegen, oder hat das auch nen anschaulichen Hintergrund (weil Integral entspricht ja der Fläche unter der Kurve )???    |
Den Schritt verstehe ich auch nicht. Könntest du bitte noch eine Antwort darauf geben? 
|
|
 |
Eddy17
Gast
|
 Eddy17 Verfasst am: 12. Jan 2010 17:11 Titel: Eddy17 Verfasst am: 12. Jan 2010 17:11 Titel: |
 |
|
Aaaaalso fangen wir mal an..
Ihr habt recht, beides beginnt mit der Maschenregel.. das Problem beim Aufladen allerdings ist, das Uc + Ur = U0 ist, und NICHT wie beim entladen Uc + Ur = 0
das macht die sache etwas komplizierte, man muss direkt die erste formel (maschenregel) ableiten, da die zeitliche ableitung von U0 = 0 ist.. rest geht weiter wie bisher..
Anderes Thema: Der logarithmus taucht als stammfunktion einer jeden Integralrechnung auf, die folgend aussieht:
Integral von: f'(x) / f(x) = [ln f(x)]
ganz einfach, is die einzige mathematische voraussetzung zu dem thema.
btw bei der Aufladung arbeitet man mit der zeitlichen ableitung von I / dem Strom. bei der entladung jedoch mit der ableitung von Q (ladung)
hoffe ich konnte euch weiterhelfen.. ist an sich nicht so komplex.. die ln funktion wird dann mit e (eulersche zahl) aufgehoben und zackbäm erhält man für die aufladung die FOrmel I(t) = I(0) * e^[(-1/RC)*t]
sry wegen den formeln, bin aber selbst auf der suche und nur über das thema gestolpert und hab das in 10mins zusammengeschrieben.. viel erfolg!
|
|
 |
andy89
Gast
|
 andy89 Verfasst am: 15. März 2012 09:53 Titel: andy89 Verfasst am: 15. März 2012 09:53 Titel: |
 |
|
Hallo,
ich hätte noch eine Frage, ich verstehe das mathematische Vorgehen und auch das Aufladen. Allerdings habe ich ein Problem beim Entladen:
Der Kondensator ist also mit einer gewissen Spannung aufgeladen, wenn ich ihn dann über einen Widerstand entlade, wirkt dann nicht der Spannungsverlust am Widerstand der Spannung am Kondensator entgegen?
Dementsprechend hätte ich dann nach der Maschenregel statt uc + uR = 0 -> uc - uR = 0.
Wo liegt mein Denkfehler?
Danke fürs Weiterhelfen
Gruß Andy
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. März 2012 10:10 Titel: GvC Verfasst am: 15. März 2012 10:10 Titel: |
 |
|
Wo ein Minus- und ein Pluszeichen hinkommt, hängt davon ab, wie Du Spannungs- und Strompfeile in Dein Schaltbild einzeichnest und wie Du den Umlaufsinn bei der Anwendung des Maschensatzes wählst. Mach' Dir 'ne Skizze, stell' sie hier vor, und dann stell' Deine Fragen dazu. Vorher hat die ganze Diskutiererei keinen Zweck.
Und wenn Du erstmal die Skizze mit allen Strom- und Spannungspfeilen gemacht hast, hast Du möglicherweise keine Fragen mehr, weil alles bereits geklärt ist.
|
|
 |
andy89
Gast
|
 andy89 Verfasst am: 15. März 2012 11:44 Titel: andy89 Verfasst am: 15. März 2012 11:44 Titel: |
 |
|
Leider klappt das mit der Skizze nicht. Am PC bin ich viel zu unfähig für eine Skizze. Leider ist aber auch mein Smartphone kaputt und bei allen anderen Handys, mit denen ich das jetzt versucht habe, ist das Bild zu unscharf, wenn ich es auf den PC übertrage. Wäre nett, wenn mir trotzdem jemand helfen könnte.
Ich versuche es nochmal in Worten auszudrücken. Aus meiner falschen Sicht dreht sich die Richtung der Spannung an dem Widerstand um.
Beim Aufladen wirkt er entgegen der Spannung der Quelle. Also gilt laut Maschenregel:
Spannung Quelle = Spannung Widerstand + Spannung Kondensator
Beim Entladen gilt aber Spannung Kondensator = Spannung Widerstand ( da sich ja die Stromrichtung ändert, ändert sich auch die "Richtung" der Spannung des Widerstandes?
Gruß
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. März 2012 12:39 Titel: GvC Verfasst am: 15. März 2012 12:39 Titel: |
 |
|
Noch einmal: Es ist doch sch...egal, wie die Spannungen und der Strom eingezeichnet sind. In jedem Fall muss gelten:
1. der Maschensatz
2. das ohmsche Gesetz
3. die Strom-/Spannungsbeziehung am Kondensator
Und wenn Du diese Gesetzmäßigkeiten vorzeichenrichtig anwendest, erhältst Du jedesmal dieselbe Gleichung.
Vorzeichenrichtig heißt beispielseise
 wenn uR und i in gleiche Richtung weisen, aber wenn uR und i in gleiche Richtung weisen, aber
 wenn uR und i entgegengerichtet eingezeichnet sind wenn uR und i entgegengerichtet eingezeichnet sind
EDIT: Habe hier das Minuszeichen eingefügt, welches mir irgendwie abhanden gekommen war.
 wenn uC und i in gleiche Richtung weisen, aber wenn uC und i in gleiche Richtung weisen, aber
 wenn uC und i entgegengerichtet eingezeichnet sind wenn uC und i entgegengerichtet eingezeichnet sind
Zuletzt bearbeitet von GvC am 15. März 2012 13:47, insgesamt einmal bearbeitet |
|
 |
andy89
Gast
|
 andy89 Verfasst am: 15. März 2012 13:07 Titel: andy89 Verfasst am: 15. März 2012 13:07 Titel: |
 |
|
Danke, das hat mir weitergeholfen. Mir war mit den Vorzeichen nicht wirklich bewusst, dass wenn ich die Richtung der Spannung ändere sich einfach nur das Vorzeichen ändert.
Gruß
|
|
 |
ET-Tutorials
Anmeldungsdatum: 01.04.2010
Beiträge: 11
|
 ET-Tutorials Verfasst am: 17. März 2012 11:58 Titel: Meine VIDEO-Reihe zum Thema Kondensator ET-Tutorials Verfasst am: 17. März 2012 11:58 Titel: Meine VIDEO-Reihe zum Thema Kondensator |
 |
|
Ich habe eine VIDEO-Reihe zum Thema Kondenator erstellt.
Vielleicht ist das für den einen oder anderen interessant:
Link gelöscht. Bitte das Forum nicht für Werbung missbrauchen. Steffen
|
|
 |
Pädagoge
Anmeldungsdatum: 29.04.2022
Beiträge: 5
|
 Pädagoge Verfasst am: 31. Jan 2023 14:38 Titel: Pädagoge Verfasst am: 31. Jan 2023 14:38 Titel: |
 |
|
Ich würde gerne diesen etwas älteren Forumsbeitrag wiederbeleben.
Ich stehe vor dem gleichen Problem wie andy89.
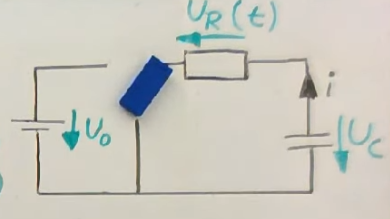
Würde ich beim Entladen des Kondensators über die Maschenregel argumentieren, müsste die Gleichung U_C=U_R lauten und nicht U_C=-U_R.
Um dem Wunsch nach einer Skizze nachzukommen, habe ich ein Bild angefügt.
Netzrecherche war erfolgslos, hoffe mir kann jemand weiterhelfen.
lg
| Beschreibung: |
|
| Dateigröße: |
60.2 KB |
| Angeschaut: |
12928 mal |
|
|
|
 |
Pädagoge
Anmeldungsdatum: 29.04.2022
Beiträge: 5
|
 Pädagoge Verfasst am: 07. Feb 2023 15:53 Titel: Pädagoge Verfasst am: 07. Feb 2023 15:53 Titel: |
 |
|
Ist die Frage doof? Ist die Frage zu schwierig? Ist die Frage zu aufwändig, um sie zu beantworten?
Ich versuche nochmals etwas mehr Informaton zu liefern, weshalb ich die Thematik nicht verstehe:
Im Netz findet man auf meine Frage z.B. die Antwort, "na ist doch klar, weil der Strom negativ ist (-dQ/dt)" (deutlich sachlicher formuliert, aber das ist der Kern der Aussage). Und ich finde das eben nicht klar, sondern für mich wirkt das bisschen so nach dem Motto: "Ich mache mir dir Welt, wie sie mir gefällt" (Ich hoffe das war nicht zu provokativ).
Ich weiß wie die Spannungs- und Stromverläufe aussehen und passe meine Mathematik entsprechend an. Aber das kann es doch nicht sein? Es kann doch nicht sein, dass man zum Llösen der DGL zusätzliche Information einfließen lassen muss.
Bisher komme ich nicht drauf, was ich offenbar noch nicht verstehe.
Ich weiß nicht, ob ich das Problem damit verständlich umrissen habe. Freue mich über jegliche Rückmeldung.
Habt vielen Dank.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 07. Feb 2023 17:01 Titel: as_string Verfasst am: 07. Feb 2023 17:01 Titel: |
 |
|
Hallo!
Ich weiß nicht genau, ob ich Deine Frage überhaupt verstehe...
Wenn Du die Masche z. B. einmal rundrum im Uhrzeigersinn gehst, dann wird doch das Potential am einen Bauteil um denselben Betrag geringer, wie es am anderen höher wird. Da Spannung Potential-Differenz ist, hast Du dann einmal eine positive und einem eine negative Spannung. Ich habe keine Ahnung, warum Du meinst, die seien doch beide positiv.
Maschenregel funktioniert ja so: Gehe entlang einer Masche in eine Richtung im Kreis (also entweder links-rum oder rechts-rum, entgegen oder im Uhrzeigersinn, nicht eine Himmelsrichtung sondern eine "Drehrichtung"). Dann muss ja logischerweise dasselbe Potential wieder erreicht werden, wenn Du an der identischen Stelle in der Masche wieder angekommen bist. Mehr besagt ja letztlich die Maschenregel nicht. Du musst dann halt die Spannung an allen Bauteilen, bei der das Potential geringer wird, negativ zählen und umgekehrt.
Oder was genau ist Deine Frage? Ich glaube, ich verstehe sie wirklich nicht...
Gruß
Marco
|
|
 |
Pädagoge
Anmeldungsdatum: 29.04.2022
Beiträge: 5
|
 Pädagoge Verfasst am: 07. Feb 2023 17:58 Titel: Pädagoge Verfasst am: 07. Feb 2023 17:58 Titel: |
 |
|
Hallo as-string,
danke, dass du an meinem Leiden interessiert bist! Freut mich wirklich!
Neko hat den Spannungsverlauf beim Entladen des Kondensators C über den Widerstand R vorgerechnet. Beim Lösen der DGL kommt der korrekte Spannungsverlauf raus. So weit so gut. (Habe es nochmals im Anhang angefügt)
Wenn ich entsprechend der Maschenregel die DGL aufstelle, lautet diese aber nach meinem Verständnis und auch nach deinem, wenn ich deinen Beitrag durchlese, eben nicht  , sondern , sondern  . .
Die Folge wäre ein Vorzeichenwechsel im Exponenten des Spannungsverlaufs, was eben nicht dem korrekten Spannungsverlauf bei der Entladung entspricht, sondern eben schon so wie von Neko vorgerechnet und wie es auch überall sonst zu finden ist.
Warum hier aber die Maschenregel scheinbar nicht erfüllt sein soll, darauf geht nirgendwo jemand ein. Aus der Perspektive wie Neko das herleitet und auch überall sonst so gemacht wird, macht das vielleicht zunächst Sinn, aber wenn man genauer darüber nachdenkt eben nicht.
Manche argumentieren dann, ja, weil der Strom negativ ist (-dQ/dt), kommt die korrekte Gleichung }{\dd t} + \frac{1}{RC} Q(t)=0 ) eben doch zu Stande. eben doch zu Stande.
Es kann aber doch nicht sein, dass man die Information des Stroms "von außen" einfließen lassen muss. Das wirkt einfach nur "zusammengemurkst" bis die Welt wieder i.O. ist.
lg
| Beschreibung: |
|
| Dateigröße: |
26 KB |
| Angeschaut: |
12666 mal |

|
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
 ML Verfasst am: 07. Feb 2023 18:12 Titel: ML Verfasst am: 07. Feb 2023 18:12 Titel: |
 |
|
Hallo,
im Prinzip hat GvC vor 12 Jahren schon alles Wesentliche gesagt. Zumindest vermute ich, dass Dir das Vorzeichen in der Bauelementegleichung nicht geläufig ist. Wir gehen aber nochmal Schritt für Schritt durch und Du sagst dann, an welcher Stelle Du die willkürlichen Vorzeichen siehst, die Dir die Bauchschmerzen verursachen.
| Pädagoge hat Folgendes geschrieben: |
Würde ich beim Entladen des Kondensators über die Maschenregel argumentieren, müsste die Gleichung U_C=U_R lauten und nicht U_C=-U_R.
|
Das ist so richtig.
Grundsätzlich legst Du durch Angabe der Pfeile für Stromstärke und Spannung die Einbaurichtung der Messgeräte fest, und zwar so:
Pfeilbasis = rotes Kabel (Innenleiter beim Oszilloskop)
Pfeilspitze = schwarzes/blaues Kabel (Außenleiter beim Oszilloskop)
Zeigt das Messgerät dann einen positiven Strom an, so fließt ein technischer Strom in Pfeilrichtung. Zeigt das Messgerät eine positive Spannung an, dann ist die Pfeilbasis positiv gegenüber der Spitze.
Mit Deiner Bepfeilung lauten die Bauelementgleichungen wie folgt:
 = R \cdot i(t)) und und
 = -C \cdot \frac{\mathrm{d}u_\mathrm{C}(t)}{\mathrm{d}t})
Das negative Vorzeichen in der Bauelementgleichung für den Kondensator ist bei der vorgenommenen Bepfeilung zwingend*. Die Gleichung gilt ohne das Vorzeichen, wenn das i durch das Bauelement und das u am Bauelement in die gleiche Richtung zeigen.
Die Maschenregel lautet nun, wie Du richtig festgestellt hast:
 = u_\mathrm{C}(t))
Setzt man die Gleichungen ineinander ein und lässt den Index für die Spannnung weg, d. h.  := u_\mathrm{R}(t) = u_\mathrm{C}(t)) , so ergibt sich die DGL: , so ergibt sich die DGL:
 = -RC \cdot \frac{\mathrm{d}u(t)}{\mathrm{d}t}) mit mit  = U_0) . .
Wir nehmen einen Exponentialansatz  = A \cdot \mathrm{e}^{Bt}) , dann folgt zunächst durch Einsetzen von , dann folgt zunächst durch Einsetzen von  der Wert der Wert 
Wir haben also:  = U_0 \cdot \mathrm{e}^{Bt})
Eingesetzt in die DGL ergibt sich:  . .
Teilen durch  führt zu führt zu  . .
Insgesamt ist also:
 = U_0 \cdot \mathrm{e}^{\frac{-t}{RC}}) . .
Viele Grüße
Michael
* Hätte man den Pfeil für die Stromstärke ) anders herum eingezeichnet, so würde gelten anders herum eingezeichnet, so würde gelten  = -R \cdot i(t)) . Egal, was man macht, eine der Gleichungen sieht "doof" aus. . Egal, was man macht, eine der Gleichungen sieht "doof" aus.
|
|
 |
Pädagoge
Anmeldungsdatum: 29.04.2022
Beiträge: 5
|
 Pädagoge Verfasst am: 10. Feb 2023 14:51 Titel: Pädagoge Verfasst am: 10. Feb 2023 14:51 Titel: |
 |
|
Hallo Michael,
Zunächst: Danke, dass du, was GvC bereits beschrieb, nochmals auf den Punkt gebracht hast. Das habe ich gebraucht.
Entschuldige meine verspätete Rückmeldung, ich musste mir zunächst Gedanken dazu machen.
Es ist so wie du sagst. Mir ist die Vorzeichenkonvention nicht geläufig.
Ich kann dir in dem konkreten Beispiel folgen, bin aber noch nicht ganz zufrieden, da es mir im Allgemeinen noch nicht ganz verständlich ist.
Die Bepfeilung scheint nicht vollkommen willkürlich machbar. Nach etwas Ausprobieren am Beispiel des Aufladens des Kondensators würde ich schlussfolgern, dass bei (idealen) Quellen Spannung und Strom nie in die gleiche Richtung zeigen können (Vermutung: Ausnahme mehrere Quellen). Wenn ich das beherzige komme ich unabhängig von der restlichen Bepfeilung immer auf dasselbe Ergebnis.
Bitte um Korrektur oder Hinweis, falls ich inkorrekt oder unvollständig schlussfolgere.
Vielen Dank!
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
 ML Verfasst am: 10. Feb 2023 16:20 Titel: ML Verfasst am: 10. Feb 2023 16:20 Titel: |
 |
|
Hallo,
| Zitat: |
Nach etwas Ausprobieren am Beispiel des Aufladens des Kondensators würde ich schlussfolgern, dass bei (idealen) Quellen Spannung und Strom nie in die gleiche Richtung zeigen können (Vermutung: Ausnahme mehrere Quellen).
|
Ja, es ist richtig: Wenn Du eine Spannungsquelle an einen Ohm'schen Widerstand anschließt, fließt in der Spannungsquelle der Strom gegen die dort (scheinbar) herrschende Feldrichtung.
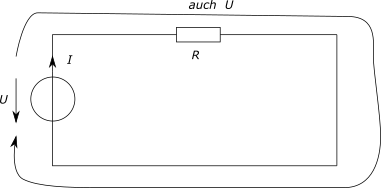
Im Sinne von Bild 1 gilt:

so dass in der Quelle Stromstärke und Spannung entgegengesetzt zeigen.
Spannungs- und Strommessgeräte zeigen dann die gleichen Vorzeichen an.
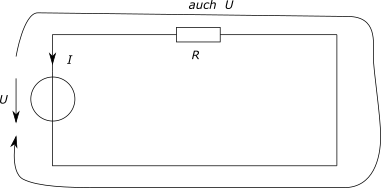
Aber weshalb sollte es verboten sein, das Messgerät für die Stromstärke umzudrehen? Dann lautet die Zeichnung wie in Bild 2, und es gilt entsprechend:

Die Anzeigewerte von Stromstärke und Spannung haben hier umgekehrte Vorzeichen.
Die Bepfeilung ist genauso willkürlich wie die Einbaurichtung der Messgeräte.
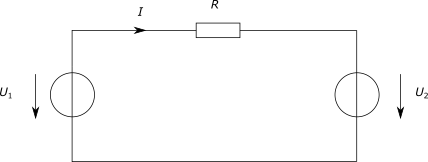
Besonders klar wird das in Bild 3. Je nachdem, ob  oder oder  ist, fließt der Strom mal in die eine, mal in die andere Richtung. ist, fließt der Strom mal in die eine, mal in die andere Richtung.
Bild 3 kann man als ein Prinzipschaltbild für ein Batterieladegerät sehen.
Wenn U1 das Ladegerät und U2 die Batterie sind, findet der Ladevorgang statt, wenn U1 > U2 ist.
Viele Grüße
Michael
| Beschreibung: |
|
| Dateigröße: |
5.11 KB |
| Angeschaut: |
12523 mal |
|
| Beschreibung: |
|
| Dateigröße: |
5.12 KB |
| Angeschaut: |
12523 mal |
|
| Beschreibung: |
|
| Dateigröße: |
3.7 KB |
| Angeschaut: |
12523 mal |
|
|
|
 |
Pädagoge
Anmeldungsdatum: 29.04.2022
Beiträge: 5
|
 Pädagoge Verfasst am: 11. Feb 2023 16:26 Titel: Pädagoge Verfasst am: 11. Feb 2023 16:26 Titel: |
 |
|
Hallo Michael,
Ich habe den (Vorzeichen-) Fehler bei meinen Experimenten gefunden und sehe zwischen Theorie und Praxis keine Uneinigkeit mehr.
Hab vielen Dank für deine gehaltvollen Beiträge, auch über dieses Thema hinaus . 
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
 ML Verfasst am: 12. Feb 2023 21:13 Titel: ML Verfasst am: 12. Feb 2023 21:13 Titel: |
 |
|
Hallo,
| Pädagoge hat Folgendes geschrieben: |
Hab vielen Dank für deine gehaltvollen Beiträge, auch über dieses Thema hinaus .  |
Freut mich, dass es Dir nutzt. 
Viele Grüße
Michael
|
|
 |
|





























