| Autor |
Nachricht |
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
 verlorenerPhysiker Verfasst am: 17. Aug 2014 13:04 Titel: Allgemeine Lösung Newtonsche Bewegungsgleichung Energieerhal |
 |
|
Meine Frage:
Hallo,
ich habe folgende Fragestellung:
Ein punktförmiges Teilchen der Masse m=2kg bewege sich in einer Dimension unter dem Einfluss der Kraft
=24\sqrt{|x|} - 32x ) .
(a) Stellen sie die Kraft F durch ein Potential V(x) mit V(0)=0 dar. Skizzieren sie V(x).
(b) Geben Sie ausgehend vom Konzept der Energieerhaltung die allgemeine Lösung der newtonschen Bewegungsgleichung in Form eines Integrals an. Bestimmen Sie nun für den Spezialfall E=0 die nichttriviale Lösung.
Meine Ideen:
Die Aufgabe a konnte ich problemlos lösen.. nur bei der b hab ich keine Ahnung wie ich auf die allgemeine Lösung der newtonschen Bewegungsgleichung komme..
Wie stelle ich denn die allgemeine Bewegungsgleichung auf?
Ich kann die von einem harmonischen ungedämpften Oszillator aufstellen aber diese irgendiwe nicht..
Ich würde vielleicht:
=24\sqrt{|x|} - 32x = mx'' )
schreiben aber das hat ja nicht viel mit Energieerhaltung zu tun..
EDIT: Was natürlich der Fall ist, ist dass ich eine kinetische Energie habe die natürlich  ist.. |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 17. Aug 2014 13:23 Titel: |
|
|
Die Idee hinter der Energieerhaltung ist die Reduktion der Bewegungsgleichung zweiter Ordnung auf eine DGL erster Ordnung. Du schreibst
)
sowie
Die Terme in E sind nicht explizit zeitabhängig, d.h. E = const. entlang einer Lösung x(t). Du führst nun eine Trennung der Variablen durch, d.h. du formst die Gleichung E = ... um zu
)
In der Funktion f(x) ist dein Potential V(x) sowie E als Parameter enthalten.
Anschließend kannst du beide Seiten separat integrieren, d.h.
} dx\,f_E(x))
Dieses Integral ist zu lösen sowie anschließend von t(x) nach x(t) aufzulösen. Außerdem must du die Integrationskonstanten aus den Anfangsbedingungen bestimmen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 13:48 Titel: |
|
|
Also habe ich dann:
 = \frac{m}{2} \frac{dx^{2}}{dt^{2}} )
bzw: )}{m}} )
und demnach: )}{m}} \, dx
<br />
)
ist das bis hierhin schonmal richtig so? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 17. Aug 2014 13:52 Titel: |
|
|
ja, passt
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 13:59 Titel: |
|
|
setze ich denn jetzt auch V(x) in die Gleichung ein? Das sollte ich ja in der Aufgabe davor bestimmen  |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 17. Aug 2014 14:00 Titel: |
|
|
Klar, jetzt musst du V( x) einsetzen
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 14:06 Titel: |
|
|
kurzer check noch:
ich habe V(x) wie folgt bestimmt:
ist das soweit korrekt? ich hab eig eine Thilde über dem x aber ich weiß nicht wie das mit LaTex funktioniert  |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 14:41 Titel: |
|
|
| verlorenerPhysiker hat Folgendes geschrieben: | Also habe ich dann:
)}{m}} \, dx
<br />
)
|
ist falsch.. es muss lauten:
)}{m}}} \, dx
<br />
) |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 14:47 Titel: |
|
|
Hi,
zum einen musst du auf deine Vorzeichen achten. Definitionsgemäß ist ja:
Also hier:
 = - \frac{dV}{dx})
Damit
 dx'} = - \int{\frac{dV}{dx'} dx'} = V_0 - V(x))
Für die übliche Wahl  = 0) , also
 = - \int{F(x') dx'} )
Also "minus". Ansonsten ist dein Integral (Potential) fast richtig - der Vorfaktor vor der Wurzel stimmt m.E. nicht. |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 15:07 Titel: |
|
|
Ja stimmt 
dann hab ich jetzt folgendes:
Da E ja konstant ist, kann ich E einfach als Variable betrachten..
Nur wie löse ich am besten das Integral? Mich stört die Wurzel im Nenner, sonst könnte ich vll den arcsin verwenden..
Allerdings steht in der Aufgabe, dass ich es in Form eines Integrals angeben soll.. muss ich es demnach lösen? |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 15:13 Titel: |
|
|
| verlorenerPhysiker hat Folgendes geschrieben: | Ja stimmt
dann hab ich jetzt folgendes:
Da E ja konstant ist, kann ich E einfach als Variable betrachten..
|
Dein jetzt angegebenes Potential  = -32\sqrt{|x|^3}-16x^2) stimmt immer noch nicht. Mach doch mal die Probe, und leite dein gefundenes ) nach  ab - kommst du dann wieder auf )
| Zitat: |
Nur wie löse ich am besten das Integral? Mich stört die Wurzel im Nenner, sonst könnte ich vll den arcsin verwenden..
Allerdings steht in der Aufgabe, dass ich es in Form eines Integrals angeben soll.. muss ich es demnach lösen? |
Zunächst: Was steht denn über die Konstante "E" in der Aufgabenstellung? Was sollst du annehmen?  |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 15:18 Titel: |
|
|
ohje,.. es ist noch schwer den Kehrwert des Exponenten zu bilden und mit dem Vorfaktor zu multiplizieren
Okay dann habe ich anstelle von -32 als Konstante -16 .. dann passt es auch beim differenzieren wieder..
Ich soll annehmen, dass E=0 ist.. gut.. dann fällt mein E in der Wurzel des Nenners weg, aber dadurch kann ich das Integral immer noch nicht so einfach lösen.. |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 15:32 Titel: |
|
|
| verlorenerPhysiker hat Folgendes geschrieben: | ohje,.. es ist noch schwer den Kehrwert des Exponenten zu bilden und mit dem Vorfaktor zu multiplizieren
Okay dann habe ich anstelle von -32 als Konstante -16 .. dann passt es auch beim differenzieren wieder..
Ich soll annehmen, dass E=0 ist.. gut.. dann fällt mein E in der Wurzel des Nenners weg, aber dadurch kann ich das Integral immer noch nicht so einfach lösen.. |
Genau, das Potential ist also:
 = -16 x^{\frac{3}{2}} + 16x^2)
Bei dem gegebenen Integral muss ich für den Moment auch passen. Da fällt mir auf die schnelle keine gescheite Substitution ein. |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 15:35 Titel: |
|
|
Auf dem Blatt steht noch als Hinweis:
 )
aber ich habe ja noch eine zusätzliiche Wurzel in der Wurzel... deswegen geht das sicherlich nicht.. und Wolfram spuckt mir auch keine Lösung aus..
EDIT: außerdem genügt es nur die positiven x-Werte zu betrachten... das hilft mir jetzt aber auch nicht weiter  |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 15:44 Titel: |
|
|
| verlorenerPhysiker hat Folgendes geschrieben: | Auf dem Blatt steht noch als Hinweis:
aber ich habe ja noch eine zusätzliiche Wurzel in der Wurzel... deswegen geht das sicherlich nicht.. und Wolfram spuckt mir auch keine Lösung aus..
EDIT: außerdem genügt es nur die positiven x-Werte zu betrachten... das hilft mir jetzt aber auch nicht weiter |
Ahja, ich glaube damit geht es. Muss meine Rechnung nochmal überprüfen, aber das kannst du ja parallel auch mal tun: Klammere mal  aus und zieh es aus der Wurzel raus. Dann steht da:
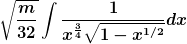
Und dann die Substitution  anwenden. Dann kommt man, wenn ich mich nicht verrechnet habe, genau auf das Integral im Hinweis.
Zuletzt bearbeitet von -Christian- am 17. Aug 2014 15:49, insgesamt 2-mal bearbeitet |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 15:46 Titel: |
|
|
|
leider ist da in der antwort was schief gegangen mit latex... |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 15:48 Titel: |
|
|
|
Sorry, hab's korrigiert! |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 16:02 Titel: |
|
|
Also ich hab dann jetzt:
}^{z(x_{0})} \! \frac{1}{ \sqrt{1-z^{2}}} \, dz = \arcsin(z)
<br />
)
bzw.
]
<br />
)
wobei ich nicht weiß wie ich mit LaTex die vierte Wurzel schreibe (das Argument im arcsin soll die vierte Wurzel sein)... und ich nicht weiß wie ich meine Integrationsgrenzen am integrierten Ausdruck anbringe...
das war ne sehr gute Idee... interessant das kein Online-Integralrechner und auch Wolframalpha nicht drauf gekommen ist.. |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 16:04 Titel: |
|
|
|
och ne.. ich darf ja kein x aus dem im integral ziehen.. wie dumm von mir.. sorry |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 16:05 Titel: |
|
|
| verlorenerPhysiker hat Folgendes geschrieben: | Also ich hab dann jetzt:
bzw.
|
Moment, erstmal musst du die Substitution richtig ausführen. Du hast vergessen das 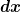 im Integral richtig zu ersetzen und damit fehlt dir noch ein entscheidender Faktor.
Außerdem ist auch beim Ausklammern von  aus der Wurzel etwas schief gelaufen.
Edit:
| verlorenerPhysiker hat Folgendes geschrieben: | | och ne.. ich darf ja kein x aus dem im integral ziehen.. wie dumm von mir.. sorry |
Ganz genau - deswegen Substitution richtig machen, dann gibt es nichts mehr zum rausziehen. |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 16:24 Titel: |
|
|
okay stimmt.. der Ausdruck im Nenner kürzt sich weg und dadurch habe ich quasi nur noch nen Faktor 1/4 zusätzlich in meinem eben geschriebenen Integral, den ich ja einfach rausziehen kann und damit musste ich mein Ergebnis nur noch um den Faktor 1/4 korregieren..
bin ich damit jetzt endlich fertig? ..
EDIT: Oh, und ich hab ein negatives Vorzeichen |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 16:26 Titel: |
|
|
|
Kommt drauf an ... was ist denn nun deine Ortskurve? Also welches Ergebnis hast du für x(t)? |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 16:32 Titel: |
|
|
keine Ahnung.. bisher keins würd ich sagen...
steh grade nach dem schwierigen Integral doch sehr auf dem Schlauch |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 16:35 Titel: |
|
|
Dann bist du auch noch nicht fertig.
Du hast jetzt eine Funktion ) dastehen. Du weißt und willst ) haben. Also: Rücksubstitution und umstellen nach . |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 16:51 Titel: |
|
|
ich hab ja das integral von  .. also lass ich den einen Ausdruck in Ruhe ... dann habe ich:
-\arcsin(\sqrt{x_{0}})]
<br />
)
(Immer noch im arcsin die vierte Wurzel)
Und dann hab ich:
=\sin(- \frac{ t-t_{0}- \frac{\sqrt{m}}{4\sqrt{32}} \arcsin(\sqrt{x_{0}})]}{\frac{\sqrt{\frac{m}{32}}}{4}})
<br />
) |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 17:13 Titel: |
|
|
Der Faktor  nach dem Integrieren ist noch falsch. Du hast doch durch die Substitution von :
Also durch "Umstellen nach dx" (auch wenn die Mathematiker das nicht gern so lesen):
Wenn du das ins Integral nach dem Ausklammern von  einsetzt, dann hast du zunächst mal:
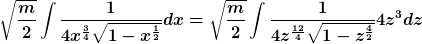
Und da kürzt sich dann doch das  raus. Ein "Minus" steht dann auch nirgends vor dem Integral. Einverstanden?
Dann hast du also als Ergebnis der Integration dastehen (wenn man von  bis z integriert):
 - \arcsin(z_0)) = \sqrt{\frac{m}{2}}(\arcsin(\sqrt[4]{x}) - \arcsin(\sqrt[4]{x_0})) )
Und dann stellst du noch um und bist fertig.
Zuletzt bearbeitet von -Christian- am 17. Aug 2014 17:26, insgesamt einmal bearbeitet |
|
|
verlorenerPhysiker
Anmeldungsdatum: 17.08.2014
Beiträge: 30
|
| verlorenerPhysiker Verfasst am: 17. Aug 2014 17:25 Titel: |
|
|
den Vorfaktor hast du jetzt einfach weggelassen?
Aber ja okay.. das macht Sinn.. da ist wohl was schief gegangen..
Vielen lieben Dank für die Hilfe!  |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 17:28 Titel: |
|
|
Den Vorfaktor  hatte ich im letzten Ausdruck vergessen - habe es gleich mal im Posting korrigiert.
| Zitat: | | Vielen lieben Dank für die Hilfe! |
Bitte, gern! |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 17. Aug 2014 17:51 Titel: |
|
|
Läuft das in der Frage ganz oben auf eine Art Schwingung hinaus?
=sin^4\left(\omega t\right)) |
|
|
-Christian-
Anmeldungsdatum: 08.07.2006
Beiträge: 199
|
| -Christian- Verfasst am: 17. Aug 2014 17:55 Titel: |
|
|
Ja, genau. Eben mit  . Ist auch ganz einsichtig, wenn man sich das Potential mal zeichnet/zeichnen lässt. |
|
|
|
Registrieren
Login
FAQ
Suchen
