| Autor |
Nachricht |
Sara02
Anmeldungsdatum: 05.11.2023
Beiträge: 6
|
 Sara02 Verfasst am: 05. Nov 2023 11:42 Titel: Normierung WeFu zwei Teilchen nicht orthogonal Sara02 Verfasst am: 05. Nov 2023 11:42 Titel: Normierung WeFu zwei Teilchen nicht orthogonal |
 |
|
Hallo,
Nach stillem Mitlesen habe ich jetzt mal eine Frage, deren Lösung ich nicht über die SuFu finden konnte.
Es geht um die Normierung einer Wellenfunktion für zwei (beispielhaft unterscheidbare) Teilchen 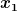 und und  mit Gesamtwellenfunktion mit Gesamtwellenfunktion
\cdot\phi_b(x_2))
(analog für Fermionen und Bosonen), wenn
 ) und und  ) nicht orthogonal zueinander stehen. nicht orthogonal zueinander stehen.
Nicht orthogonal bedeutet natürlich, dass das Integral
\cdot\phi_b(x)dx\neq0) ergibt. ergibt.
Aber was bedeutet das für das Integral
^*\psi(x_1,x_2)dx_1dx_2=\int[\phi_a(x_1)\cdot\phi_b(x_2)]^*[\phi_a(x_1)\cdot\phi_b(x_2)]dx_1dx_2) ? ?
Das rote Integral taucht ja in der Norm von 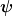 nie auf, da über unterschiedliche Teilchen integriert wird. nie auf, da über unterschiedliche Teilchen integriert wird.
Vielen Dank schonmal! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 05. Nov 2023 12:07 Titel: TomS Verfasst am: 05. Nov 2023 12:07 Titel: |
 |
|
Hallo und herzlich Willkommen.
Ich verstehe deine Frage nicht. Formuliere sie bitte nochmal um.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sara02
Anmeldungsdatum: 05.11.2023
Beiträge: 6
|
 Sara02 Verfasst am: 05. Nov 2023 12:41 Titel: Sara02 Verfasst am: 05. Nov 2023 12:41 Titel: |
 |
|
Die Frage ist:
Wie lautet die Normierung der Gesamtwellenfunktion 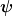 für zwei Teilchen für zwei Teilchen 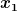 und und  , wenn , wenn ) und und ) nicht orthogonal aufeinander stehen. nicht orthogonal aufeinander stehen.
Dabei wird 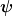 als als
=\phi_a(x_1)\cdot\phi_b(x_2)) (unterscheidbare Teilchen), (unterscheidbare Teilchen),
=\frac{1}{\sqrt{2}}(\phi_a(x_1)\cdot\phi_b(x_2)+\phi_a(x_2)\cdot\phi_b(x_1)) (Bosonen), (Bosonen),
=\frac{1}{\sqrt{2}}(\phi_a(x_1)\cdot\phi_b(x_2)-\phi_a(x_2)\cdot\phi_b(x_1)) (Fermionen) angegeben. (Fermionen) angegeben. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 05. Nov 2023 15:06 Titel: TomS Verfasst am: 05. Nov 2023 15:06 Titel: |
 |
|
Für unterscheidbare Teilchen:
 = \phi_a(x_1) \, \phi_b(x_2))
 \, \psi_{ab}(x_1, x_2) = \int_{\mathbb{R}} dx_1 \, \phi_a^\ast(x_1) \, \phi_a(x_1) \cdot \int_{\mathbb{R}} dx_2 \, \phi_b^\ast(x_2) \, \phi_b(x_2))
In den beiden anderen Fällen musst du auch die gemischten Terme betrachten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sara02
Anmeldungsdatum: 05.11.2023
Beiträge: 6
|
 Sara02 Verfasst am: 05. Nov 2023 18:29 Titel: Sara02 Verfasst am: 05. Nov 2023 18:29 Titel: |
 |
|
Danke, soweit ist es mir klar.
Aber da ist ja jetzt nirgendwo die Eigenschaft genutzt, dass 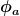 und und  nicht orthogonal sein sollen. nicht orthogonal sein sollen.
Also
\cdot\phi_b(x)dx\neq0)
Oder könnte mit "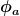 und und  seien nicht orthogonal" gemeint sein, dass deren Norm jeweils nicht 1 ist? und nicht, dass die beiden Wellenfunktionen nicht orthogonal zueinander sind? seien nicht orthogonal" gemeint sein, dass deren Norm jeweils nicht 1 ist? und nicht, dass die beiden Wellenfunktionen nicht orthogonal zueinander sind? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 05. Nov 2023 18:36 Titel: TomS Verfasst am: 05. Nov 2023 18:36 Titel: |
 |
|
| Sara02 hat Folgendes geschrieben: | Aber da ist ja jetzt nirgendwo die Eigenschaft genutzt, dass 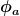 und und  nicht orthogonal sein sollen. nicht orthogonal sein sollen. |
Bisher nicht, aber schau dir mal den Fall von Bosonen und Fermionen an.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sara02
Anmeldungsdatum: 05.11.2023
Beiträge: 6
|
 Sara02 Verfasst am: 05. Nov 2023 19:12 Titel: Sara02 Verfasst am: 05. Nov 2023 19:12 Titel: |
 |
|
Danke, für Bosonen war ich gerade dabei das aufzuschreiben.
\phi_b(x_1)+\phi_b^*(x_1)\phi_a(x_1)]+\int dx_2[\phi_a^*(x_2)\phi_b(x_2)+\phi_b^*(x_2)\phi_a(x_2)])
i.A. dürften die zwei Integrale ja nicht bekannt sein, oder? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 05. Nov 2023 19:21 Titel: TomS Verfasst am: 05. Nov 2023 19:21 Titel: |
 |
|
Das stimmt nicht.
psi ist bilinear in den phis, enthält also Produkte von zwei phis; daher enthält |psi|^2 immer Produkte von vier phis, wovon immer zwei zur selben Koordinate gehören. D.h. du erhältst wiederum Produkte zweier Integrale, und jedes enthält einen Integranden mit dem Produkt zweier phis.
Schreib doch zunächst mal den Integranden auf und sortiere nach x1 und x2.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sara02
Anmeldungsdatum: 05.11.2023
Beiträge: 6
|
 Sara02 Verfasst am: 05. Nov 2023 19:30 Titel: Sara02 Verfasst am: 05. Nov 2023 19:30 Titel: |
 |
|
Dann hätte ich den letzten Schritt nicht machen dürfen:
\phi_b^*(x_2)\phi_a(x2)\phi_b(x_1)+\phi_a^*(x_2)\phi_b^*(x_1)\phi_a(x_1)\phi_b(x_2)]) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 06. Nov 2023 08:48 Titel: TomS Verfasst am: 06. Nov 2023 08:48 Titel: |
 |
|
Also wenn ich das sortiere, komme ich für die beiden Vorzeichen auf

mit

Ich sortiere in den Produkten nach x1 und x2; damit erhalte ich immer das Produkt zweier Integrale. Zwei Integrale liefern gerade die Norm, zwei das Skalarprodukt der gemischten Terme.
Wenn die beiden Wellenfunktionen normiert sind

folgt

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sara02
Anmeldungsdatum: 05.11.2023
Beiträge: 6
|
 Sara02 Verfasst am: 06. Nov 2023 10:53 Titel: Sara02 Verfasst am: 06. Nov 2023 10:53 Titel: |
 |
|
|
dankeschön, jetzt sehe ich die Umsortierung auch. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 06. Nov 2023 15:49 Titel: TomS Verfasst am: 06. Nov 2023 15:49 Titel: |
 |
|
Evtl. lohnt es sich auch, das etwas umzuformulieren:
Zerlegen wir den zweiten Zustand orthogonal bzgl. des ersten, d.h.


Dann ist
 + \xi \left( |\phi_a, \phi_x\rangle \pm |\phi_x, \phi_a\rangle \right))
D.h. die beiden Vorzeichen führen auf
)
)
Für Bosonen folgt mit der Normierung


}\|^2 = 2 - |\xi|^2)
wobei die "2" daher stammt, dass der identische Zustand "a" doppelt gezählt wird.
Für Fermionen ist dagegen explizit ausgeschlossen, dass sich beide Teilchen im identischen Zustand befinden.
D.h. es gilt

}\|^2 = 1)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 06. Nov 2023 20:11 Titel: Myon Verfasst am: 06. Nov 2023 20:11 Titel: |
 |
|
Die Normierung der Wellenfunktionen konnte ich nachvollziehen. Aber beim letzten Beitrag ist mir nicht klar, wie man für Bosonen die letzte Gleichung folgert:
| TomS hat Folgendes geschrieben: | }\|^2 = 2 - |\xi|^2) |
Und weshalb gilt für Fermionen
| Zitat: | 
}\|^2 = 1) |
Dass xi nicht gleich null sein kann, verstehe ich, sonst würde ja der Zustand auch "verschwinden". Aber weshalb muss alpha=0 sein, phi_a und phi_b also orthogonal? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 06. Nov 2023 22:14 Titel: TomS Verfasst am: 06. Nov 2023 22:14 Titel: |
 |
|
Für Fermionen muss man das Pferd von hinten aufzäumen. Im Zwei-Fermionen-Zustand kommt keine aa-Komponente vor, also ist alpha zunächst beliebig. Aber der Gesamtzustand soll letztlich auch normiert sein, daraus folgt ein Betrag von xi gleich Eins, und alpha damit Null. Natürlich könnte man den a-Teil in b immer mitnehmen, aber das ist doch sinnlos.
Für Bosonen berechnet man die Norm des zuvor konstruierten Zweiteilchen-Zustandes und eliminiert dann alpha mit der Normierungsbedingung des Einteilchen-Zustandes.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 07. Nov 2023 09:57 Titel: Myon Verfasst am: 07. Nov 2023 09:57 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Für Bosonen berechnet man die Norm des zuvor konstruierten Zweiteilchen-Zustandes und eliminiert dann alpha mit der Normierungsbedingung des Einteilchen-Zustandes. |
Aber wie bilde ich ein Skalarprodukt aus den kets des Zweiteilchenzustands, ich muss das ja irgendwie durch die Einteilchenzustände ausdrücken? Ich weiss, eine blöde frage, ich würde wohl besser einfach wieder bei den Grundlagen nachlesen als hier reinzuquatschen... ich habe so fast alles vergessen, was ich mal wusste, dass es immer wieder frustrierend ist.
Was mich bei den Fermionen halt etwas verwirrt ist: für die Eingangsfrage nach der Normierung von
=\frac{1}{\sqrt{2}}(\phi_a(x_1)\cdot\phi_b(x_2)\pm\phi_a(x_2)\cdot\phi_b(x_1)))
kam man auf

Im Aufgabentext wurde offenbar noch gesagt, dass phi_a und phi_b nicht orthogonal zueinander sein sollen.
Wenn phi_a und phi_b jeweils normiert sind, kann psi anderseits nur normiert sein, wenn

Doch das würde ja dann auch für Bosonen gelten? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 07. Nov 2023 10:47 Titel: TomS Verfasst am: 07. Nov 2023 10:47 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Aber wie bilde ich ein Skalarprodukt aus den kets des Zweiteilchenzustands, ich muss das ja irgendwie durch die Einteilchenzustände ausdrücken? |
Dazu betrachtet man zunächst

Letzteres entspricht der Definition mittels Tensorprodukt.
Dann definiert man

(und zeigt, dass diese Definition tatsächlich die Eigenschaften eines Skalarproduktes aufweist)
Das kann man dann gerne durch Integrale über Koordinaten ausdrücken. Die Reihenfolge der Kets entspricht der Nummerierung der Teilchen und damit der Koordinaten 1,2... Die Verallgemeinerung auf Linearkombinationen sollte klar sein.
Zur
| Myon hat Folgendes geschrieben: | | ... Eingangsfrage nach der Normierung ... |
Der Zustand
 )
mit normierten Einteilchenzuständen führt auf

mit

(für reelle Vektorräume ist das Skalarprodukt reell und reduziert sich auf den Cosinus des Zwischenwinkels)
Siehe auch die Cauchy-Schwarz-Ungleichung
Damit ist der Zweiteilchenzustand nicht automatisch normiert.
Das ist auch klar, denn speziell für

gilt unmittelbar
 = \sqrt{2} \, |\phi_a, \phi_a \rangle )
 = 0 )
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 07. Nov 2023 17:03 Titel: TomS Verfasst am: 07. Nov 2023 17:03 Titel: |
 |
|
Noch eine Anmerkung:
Übersichtlicher wird's, wenn man zu bosonischen (-) bzw. fermionischen (+) Erzeugern und Vernichtern übergeht.


mit

Sei außerdem

Dann definiert man


Die entsprechenden Zustände werden erzeugt mittels

 \, |0\rangle)
 \, |0\rangle = \cos\theta \cdot \left(A_{m}^\dagger\right)^2 \, |0\rangle + e^{i\gamma} \sin\theta \cdot A_m^\dagger A_n^\dagger \, |0\rangle )
Für Bosonen bzw. Fermionen liefert dies


wobei die Zahlen in den Kets die Besetzungszahlen des m-ten bzw. des n-ten Zustandes beschreiben; diese Kets sind normiert, daher tritt "Wurzel 2" explizit auf.
Für Fermionen muss der Sinus gleich Eins sein. Man erzeugt nie Zustände mit identischen Teilchen, dies folgt automatisch aus den Kommutatorrelationen bzw. aus
^2 = 0)
Für Bosonen weiß man, dass orthonormierte Zustände N identischer Teilchen der Sorte n mittels geeigneter Erzeuger
^N}{\sqrt{N!}} )
dargestellt werden. Also folgt der normierte Zustand mittels
^2}{\sqrt{2}} \, |0\rangle + e^{i\gamma} \sin\theta \cdot A_m^\dagger A_n^\dagger \, |0\rangle )
Das ist einfach eine Superposition aus "(zwei Teilchen der Sorte m) und (ein Teilchen der Sorte m sowie eines der Sorte n)". Verwendet man von vorneherein diese n-Teilchen-Erzeuger und -Zustände, so taucht die Problematik der Normierung überhaupt nicht auf. Außerdem muss man nicht ständig die lästige Symmetrisierung bzw. Antisymmetrisierung ausschrieben - was für mehr als drei Teilchen die Hölle wäre - die Operatoren erledigen das kompakt und automatisch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|















