| Autor |
Nachricht |
Forensiker
Gast
|
 Forensiker Verfasst am: 24. Aug 2015 14:53 Titel: Teilchen <=> Ensemble Forensiker Verfasst am: 24. Aug 2015 14:53 Titel: Teilchen <=> Ensemble |
 |
|
Meine Frage:
Hallo,
ich lerne derzeit Quantenmechanik (für nicht-Physiker) und habe folgendes Verständnisproblem:
Soweit ich das richtig verstanden habe kann man in der QM nur sinnvoll von einem Zustand sprechen wenn man ein Ensemle von Teilchen betrachtet.(z.B ein Elektronenstrahl),jetzt bin ich bei Potentialproblemen angelangt, wo plötzlich nur mehr von EINEM Teichen die Rede ist.Wenn ich z.B. das Elektron in einem Wasserstoffatom betrachte dann könne sich diese Zustände (k,l,m) doch nurmehr auf ein Teilchen und nicht auf ein Ensemble beziehen....
Ich bitte um Aufklärung und danke im Voraus!
Meine Ideen:
leider keine umso mehr dankbar für Hilfe! |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 24. Aug 2015 15:28 Titel: Re: Teilchen <=> Ensemble jh8979 Verfasst am: 24. Aug 2015 15:28 Titel: Re: Teilchen <=> Ensemble |
 |
|
| Forensiker hat Folgendes geschrieben: |
Soweit ich das richtig verstanden habe kann man in der QM nur sinnvoll von einem Zustand sprechen wenn man ein Ensemle von Teilchen betrachtet.(z.B ein Elektronenstrahl), |
Ich denke, dass diese Aussage nicht richtig ist. Man kann sehr wohl sinnvoll von einem Teilchen sprechen. Da man allerdings nur Übergangswahrscheinlichkeiten ausrechnen* kann (z.B. zwischen Energieniveaus, oder bei Streuung), kann man bei einer Messung eines einzelnen Teilchens keine Aussage machen, sondern nur wenn man viele Messungen durchführt.
Zum Beispiel können die erlaubten Energieeigenwerte in einem Potential auch für ein einzelnes Teilchen berechnet werden, aber mögliche Uebergangswahrscheinlichkeiten zwischen diesen Niveaus nur an vielen solchen Teilchenübergängen gemessen werden.
*Dies ist eine inhärente Eigenschaft der QM und hat nichts mit dem wirklichen "Ausrechnen" zu tun. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Aug 2015 15:34 Titel: Re: Teilchen <=> Ensemble TomS Verfasst am: 24. Aug 2015 15:34 Titel: Re: Teilchen <=> Ensemble |
 |
|
| Forensiker hat Folgendes geschrieben: | | Soweit ich das richtig verstanden habe kann man in der QM nur sinnvoll von einem Zustand sprechen wenn man ein Ensemle von Teilchen betrachtet ... |
Das ist so nicht richtig, und entsprechende Interpretationen der QM sind umstritten.
Richtig ist, dass viele (nicht alle!) Interpretationen der QM behaupten, dass die Wahrscheinlichkeit, ein Quantensystem in einem bestimmten Zustand zu finden, abhängig ist vom Quantenzustand (bzw. der Wellenfunktion). Wenn also ein Zustand psi vorliegt und nach der Wahrscheinlichkeit für den Zustand phi_n gefragt wird, dann folgt diese Wahrscheinlichkeit aus
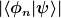
Daraus scheint nun die Ensemble-Interpretation zu folgen, denn Wahrscheinlichkeiten sollten Häufigkeiten entsprechen.
Nun ist es jedoch so, dass die QM auch besagt, dass prinzipiell erlaubte Messergebnisse einer Observablen A immer exakt den Eigenwerten dieser Observablen entsprechen. Im Falle des Wasserstoffatoms interessiert dabei insbs. Drehimpuls und Energie, die aus den Quantenzahlen n und l berechenbar sind.
Wenn man nun die Ensemble-Interpretation der QM anwendet, also bestreitet, dass der Quantenzustand irgendeine Bedeutung für ein einzelnes Quantenobjekt hätte, sondern dass dieser Zustand rein statistisch interpretiert werden muss, dann bleibt unverständlich, wieso offensichtlich einzelne Quantenobjekte dieser Regel folgen. Man kann ja einzelne Quantenobjekte in genau einem Zustand präparieren (z.B. nlm = 200 im H-Atom), jedes einzelne Atom messen, und dies für jedes einzelne Atom (nlm = 200) verifizieren (Abweichungen resultieren nicht prinzipbedingt aus der QM, sondern aus technischen Einschränkungen bei Präparation; das Experiment kann z.B. mit 100 Atomen an zehn verschiedenen Orten der Welt in zehn aufeinander folgenden Jahren durchgeführt werden).
Man kann eines rein statistische bzw. Ensemble-Intepretation der vornehmen (siehe z.B. Ballantine), muss dies jedoch nicht tun, sondern kann den Quantenzustand durchaus als "für ein einzelnes Quantenobjekt gültig" auffassen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Herbst
Anmeldungsdatum: 08.08.2015
Beiträge: 7
|
 Herbst Verfasst am: 24. Aug 2015 16:03 Titel: Re: Teilchen <=> Ensemble Herbst Verfasst am: 24. Aug 2015 16:03 Titel: Re: Teilchen <=> Ensemble |
 |
|
| TomS hat Folgendes geschrieben: | | Wenn man nun die Ensemble-Interpretation der QM anwendet, also bestreitet, dass der Quantenzustand irgendeine Bedeutung für ein einzelnes Quantenobjekt hätte, sondern dass dieser Zustand rein statistisch interpretiert werden muss, dann bleibt unverständlich, wieso offensichtlich einzelne Quantenobjekte dieser Regel folgen. Man kann ja einzelne Quantenobjekte in genau einem Zustand präparieren (z.B. nlm = 200 im H-Atom), jedes einzelne Atom messen, und dies für jedes einzelne Atom (nlm = 200) verifizieren |
Wenn der Zustand 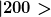 präpariert wird, der laut Ensemble-Interpretation ein Ensemble ähnlich präparierter Systeme beschreibt, ist es ziemlich trivial, wenn wir für jedes einzelne System präpariert wird, der laut Ensemble-Interpretation ein Ensemble ähnlich präparierter Systeme beschreibt, ist es ziemlich trivial, wenn wir für jedes einzelne System  "erhalten". "erhalten".
Richtig zu tragen kommt diese Interpretation erst dann, wenn wir eine Superposition aus Basiszuständen haben. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Aug 2015 17:56 Titel: Re: Teilchen <=> Ensemble TomS Verfasst am: 24. Aug 2015 17:56 Titel: Re: Teilchen <=> Ensemble |
 |
|
| Herbst hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Wenn man nun die Ensemble-Interpretation der QM anwendet, also bestreitet, dass der Quantenzustand irgendeine Bedeutung für ein einzelnes Quantenobjekt hätte, sondern dass dieser Zustand rein statistisch interpretiert werden muss, dann bleibt unverständlich, wieso offensichtlich einzelne Quantenobjekte dieser Regel folgen. Man kann ja einzelne Quantenobjekte in genau einem Zustand präparieren (z.B. nlm = 200 im H-Atom), jedes einzelne Atom messen, und dies für jedes einzelne Atom (nlm = 200) verifizieren |
Wenn der Zustand 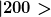 präpariert wird, der laut Ensemble-Interpretation ein Ensemble ähnlich präparierter Systeme beschreibt, ist es ziemlich trivial, wenn wir für jedes einzelne System präpariert wird, der laut Ensemble-Interpretation ein Ensemble ähnlich präparierter Systeme beschreibt, ist es ziemlich trivial, wenn wir für jedes einzelne System  "erhalten". "erhalten". |
Nein, das ist nicht trivial, da laut Ensemble-Interpretation immer nur über Ensembles geredet wird, in der Praxis jedoch einzelne, isolierte, einzelenn Quantenobjekte präpariert warden.
| Herbst hat Folgendes geschrieben: | | Richtig zu tragen kommt diese Interpretation erst dann, wenn wir eine Superposition aus Basiszuständen haben. |
Verstehe ich nicht. Ein Basiszustand |x> als ein Elemenet einer Basis B(X) bzgl. einer Observablen X kann immer als Superposition bzgl. einer anderen Basis B'(X) oder B(Y) aufgefasst werden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Herbst
Anmeldungsdatum: 08.08.2015
Beiträge: 7
|
 Herbst Verfasst am: 24. Aug 2015 22:32 Titel: Re: Teilchen <=> Ensemble Herbst Verfasst am: 24. Aug 2015 22:32 Titel: Re: Teilchen <=> Ensemble |
 |
|
| TomS hat Folgendes geschrieben: | | Nein, das ist nicht trivial, da laut Ensemble-Interpretation immer nur über Ensembles geredet wird, in der Praxis jedoch einzelne, isolierte, einzelenn Quantenobjekte präpariert warden. |
Die Präparation dieses einzelnen Quantensystems "in diesen Zustand" |nlm> ist in Wirklichkeit keine Präparation in diesen konkreten Zustand, sondern eine ("gedachte") Präparation eines Ensembles an solchen Systemen. Da aber der Eigenwert dieses einen konkreten Eigenzustands dem Messwert entspricht (Axiom), ist es nur folgerichtig, diesen auch zu erhalten. Alles andere würde der Axiomatik widersprechen.
| TomS hat Folgendes geschrieben: | | Verstehe ich nicht. Ein Basiszustand |x> als ein Elemenet einer Basis B(X) bzgl. einer Observablen X kann immer als Superposition bzgl. einer anderen Basis B'(X) oder B(Y) aufgefasst werden. |
Sorry, hatte das im Sinn:
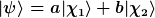
Specifies that a mixed state is a description only of the probabilities, ) and and ) of positions, not a description of actual individual positions. That is, of positions, not a description of actual individual positions. That is, ) and not and not  . In this way it is noted that a mixed state is a mixture of probabilities of physical states, not a mixture of actual physical states. (Wiki - Ensemble Interpretation) . In this way it is noted that a mixed state is a mixture of probabilities of physical states, not a mixture of actual physical states. (Wiki - Ensemble Interpretation) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Aug 2015 22:51 Titel: Re: Teilchen <=> Ensemble TomS Verfasst am: 24. Aug 2015 22:51 Titel: Re: Teilchen <=> Ensemble |
 |
|
| Herbst hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Nein, das ist nicht trivial, da laut Ensemble-Interpretation immer nur über Ensembles geredet wird, in der Praxis jedoch einzelne, isolierte, einzelenn Quantenobjekte präpariert warden. |
Die Präparation dieses einzelnen Quantensystems "in diesen Zustand" |nlm> ist in Wirklichkeit keine Präparation in diesen konkreten Zustand, sondern eine ("gedachte") Präparation eines Ensembles an solchen Systemen. Da aber der Eigenwert dieses einen konkreten Eigenzustands dem Messwert entspricht (Axiom), ist es nur folgerichtig, diesen auch zu erhalten. Alles andere würde der Axiomatik widersprechen. |
Wieso eine gedachte Präparation eines Ensembles? Der Experimentator stellt sicher, dass er immer genau ein Quantenobjekt manipuliert und präpariert. Es existiert nicht einmal Ensemble.
Natürlich ist es richtig, dass das Ergebnis der Messung nach Präparation die Axiomatik bestätigt. Aber diese Bestätigung erfolgt - wenn man das Experiment entsprechend durchführt - für jeweils ein einzelnes Quantenobjekt, nicht für Ensembles.
Der Unterschied zur statistischen Mechanik ist, dass ich dort zwingend makroskopische Ensembles betrachten muss, und dass daher die statistische Mechanik ausschließlich für Ensembles gilt. In der QM kann ich dagegen einzelne Quantenobjekte betrachten. Und die Axiome bzw. Postulate der QM gelten - mit Ausnahme des Projektions- bzw. Messpostulats auch für das einzelne Objekte. Nur ein einzelnes Postulat könnte einen dazu zwingen, die Interpretation bzgl. Einzelobjekten zugunsten von Ensembles aufzugeben. Dieser Schritt ist keineswegs zwingend (wenn auch logisch möglich).
Ich will hier keineswegs in Abrede stellen, dass die Ensemble-Interpretation eine mögliche Interpretation darstellt. Ich will lediglich klarstellen, dass man dies nicht einfach so hinnehmen sollte, um dass es sich weder um die einzig mögliche noch um eine weitverbreitete Interpretation handelt. |
|
 |
Herbst
Anmeldungsdatum: 08.08.2015
Beiträge: 7
|
 Herbst Verfasst am: 25. Aug 2015 10:38 Titel: Re: Teilchen <=> Ensemble Herbst Verfasst am: 25. Aug 2015 10:38 Titel: Re: Teilchen <=> Ensemble |
 |
|
| TomS hat Folgendes geschrieben: | | Wieso eine gedachte Präparation eines Ensembles? Der Experimentator stellt sicher, dass er immer genau ein Quantenobjekt manipuliert und präpariert. Es existiert nicht einmal Ensemble. |
Eben, weil kein Ensemble existiert und nur ein Quantenobjekt präpariert wurde, ist das Ensemble gedacht. Gleichzeitig sagt der Experimentator aber, dass er das Quantensystem in diesen Zustand präpariert hat. Ich würde dem entgegnen und behaupten, dass dieser beliebige Zustand  ein Ensemble (von diesem System, das er präpariert hat) beschreibt, d.h. würde er ein Ensemble von solchen Systemen präpariert haben, dann könnte er dieses durch diesen Zustand ein Ensemble (von diesem System, das er präpariert hat) beschreibt, d.h. würde er ein Ensemble von solchen Systemen präpariert haben, dann könnte er dieses durch diesen Zustand  beschreiben. beschreiben.
| TomS hat Folgendes geschrieben: | | Ich will hier keineswegs in Abrede stellen, dass die Ensemble-Interpretation eine mögliche Interpretation darstellt. Ich will lediglich klarstellen, dass man dies nicht einfach so hinnehmen sollte, um dass es sich weder um die einzig mögliche noch um eine weitverbreitete Interpretation handelt. |
Ich halte die Ensemble-Interpretation für die beste, aber das ist nur meine (unbedeutende) Meinung.  Die transaktionale Interpretation war für mich auch ganz interessant, für die ich auch einen Thread erstellt habe, aber leider weiß keiner dazu bescheid. So oder so, ich habe so einbisschen meine Probleme damit. Die transaktionale Interpretation war für mich auch ganz interessant, für die ich auch einen Thread erstellt habe, aber leider weiß keiner dazu bescheid. So oder so, ich habe so einbisschen meine Probleme damit.
Mich würde mal interessieren, wie viele Physiker (in %) diese oder jene Interpretation vertreten. Also Umfrage. Ich habe diesbezüglich aber noch nichts gefunden. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
|
 |
Herbst
Anmeldungsdatum: 08.08.2015
Beiträge: 7
|
 Herbst Verfasst am: 25. Aug 2015 12:44 Titel: Herbst Verfasst am: 25. Aug 2015 12:44 Titel: |
 |
|
Ui, Everett. Ist schon ziemlich crazy, aber besser als so manch andere (m.M.n. natürlich).
Danke für die Links.  |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Aug 2015 13:21 Titel: TomS Verfasst am: 25. Aug 2015 13:21 Titel: |
 |
|
| Herbst hat Folgendes geschrieben: | | Ui, Everett. Ist schon ziemlich crazy, aber besser als so manch andere |
nee, nur folgerichtig
Axiome:
1) Quantum states are represented by unit vectors in a separable Hilbert space.
2) Quantum states evolve in time according to the Schrödinger equation.
That's it!
Ich würde noch hinzufügen:
0) Quantum states and their dynamics represent the behavior of physical systems
Alles andere ist überflüssig (Kollaps, Projektionspostulat), sind Theoreme (Bornsche Regel, Dekohärenz = wechselseitige dynamischer "Unsichtbarkeit" von "Zweigen") oder Interpretationen bzw. Worte ("Welten", "Zweige", "Verzweigungen", ...). |
|
 |
Herbst
Anmeldungsdatum: 08.08.2015
Beiträge: 7
|
 Herbst Verfasst am: 25. Aug 2015 17:29 Titel: Herbst Verfasst am: 25. Aug 2015 17:29 Titel: |
 |
|
Für die Ensemble-Interpretation (EI) lassen sich diese Axiome auch hernehmen, außer dass 0) etwas umformuliert werden muss, da der Zustand ein Ensemble beschreibt.
Einen Kollaps gibt es in der EI auch nicht.Die Dekohärenz lässt sich an einem Ensemble auch erklären, m.M.n. sogar besser als bei der VWI. Das Ergebnis, die Diagonalisierung der Dichtematrix ist dann gut anschaulich und für mich gerade auch an diesem Punkt der Hinweis auf ein Ensemble.
Die Bornsche Regel lässt sich mit der EI auch "plausibel machen" oder "herleiten".
Dann kommt aber die Kritik an der VWI, insb,
https://de.wikipedia.org/wiki/Viele-Welten-Interpretation#Metaphysikeinwand
Ergebnis für mich ist dann halt, dass EI "besser" ist als VWI. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Aug 2015 21:02 Titel: TomS Verfasst am: 25. Aug 2015 21:02 Titel: |
 |
|
| Herbst hat Folgendes geschrieben: | | Für die Ensemble-Interpretation (EI) lassen sich diese Axiome auch hernehmen, außer dass 0) etwas umformuliert werden muss, da der Zustand ein Ensemble beschreibt. |
Ja, sind sie tatsächlich ausreichend?
| Herbst hat Folgendes geschrieben: | | Die Dekohärenz lässt sich an einem Ensemble auch erklären ... |
Dazu benötigt man keine Interpretation, die o.g. Axiome sowie ein konkreter Hamiltonoperator sind ausreichend.
| Herbst hat Folgendes geschrieben: | | Für... m.M.n. sogar besser als bei der VWI. |
Deswegen verstehe ich diese Aussage nicht.
| Herbst hat Folgendes geschrieben: | | Die Bornsche Regel lässt sich mit der EI auch "plausibel machen" oder "herleiten". |
Verwendet man den "Hartle frequency operator"?
Gerade diese Kritik kann ich nicht nachvollziehen.
Gegeben sei ein Produkthilbertraum sowie eine unitäre Zeitentwicklung der Form
\,|0\rangle\,|E\rangle \;\to\; (|a\rangle\,|A\rangle + |b\rangle\,|B\rangle)\,|E^\prime\rangle + \ldots)
1) Wenn es sich ausschließlich um mikroskopische Zustände handelt, dann werden alle Terme "Phänomen", das ist die seit langem bekannte Superposition (Doppelspalt, Stern-Gerlach, u.v.a.m.).
2) Wenn es sich beim ersten / zweiten / dritten Faktor um mikroskopischen System / Messgerät / Umgebung handelt, dann besteht das "Beobacher-lokale Phänomen" in einem "Zweig" in der (experimentell nachgewiesenen) Dekohärenz, d.h. in der dynamischen Unterdrückung der Sichtbarkeit anderer "Zweige".
Darf man sich aussuchen, was man Phänomen nennen möchte? Ist "destruktive Interferenz" kein Phänomen? Kannte Weizsäcker dieses Ergebnis?
Die Probleme der Everett-Interpretation sind m.E. anders geartet. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. Aug 2015 21:07 Titel: index_razor Verfasst am: 25. Aug 2015 21:07 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Axiome:
1) Quantum states are represented by unit vectors in a separable Hilbert space.
2) Quantum states evolve in time according to the Schrödinger equation.
That's it!
|
Die bedingungslose Gültigkeit (insbesondere ohne Ausnahme für den Meßprozeß) dieser beiden Axiome stellt die Ensembleinterpretation a la Ballentine ja auch voran. Die eigentlich problematischen Aspekte der Interpretation löst sie damit allerdings auch nicht. Sie hat allerdings (im Gegensatz zur Kollapsinterpretation) den Vorteil nicht zu völlig absurden Ergebnissen zu kommen. "Relative State" kenne ich noch nicht so gut um mir da ein Urteil zu erlauben.
| Zitat: |
Ich würde noch hinzufügen:
0) Quantum states and their dynamics represent the behavior of physical systems
|
Das ist m.E. so nichtssagend, daß man es auch weglassen kann. (Anhänger welcher Interpretation würden die Aussage in dieser Formulierung bestreiten?) Die eigentliche Frage ist doch: Inwiefern "repräsentiert" eine Superposition aus toter und lebendiger Katze das physikalische System "Katze"? Ein solcher Zustand repräsentiert eben eine Katze die mit Wahrscheinlichkeit soundso tot, und mit der komplementären Wahrscheinlichkeit lebendig ist. Wie würde man diese Aussage nun experimentell prüfen? Wahrscheinlich indem man eine Reihe von Katzen nach Schrödingers Vorschrift "präpariert" und nachzählt, ob die relativen Häufigkeiten stimmen. Und da hast du nun dein Ensemble.
Insgesamt ist das natürlich unbefriedigend, denn eine einzelne Katze ist ja immer entweder tot oder lebendig und man erwartet von einer vollständigen Theorie eigentlich ja Aussagen über individuelle Systeme, d.h. über die einzelnen Vertreter des Ensembles, nicht nur über das gesamte Ensemble. (So ungefähr wie in der statistischen Physik.) Anscheinend ist aber die Beschreibung des Zustands über die Wellenfunktion bereits komplett. Wie ergibt sich nun also aus der Wahrscheinlichkeitsamplitude, die den quantenmechanischen Zustand komplett beschreibt, die nachträgliche Sicherheit eines einzelnen Meßergebnisses bei einer konkreten Messung? Inwiefern erhöht die Kenntnis des Ergebnisses dieser Messung die Information über den Zustand, die vorher bereits vollständig war? Hat die Everettsche Interpretation darauf schlüssige Antworten? Keine Interpretation, die ich kenne hat sie meines Erachtens.
| Zitat: |
Alles andere ist überflüssig (Kollaps, Projektionspostulat), sind Theoreme (Bornsche Regel, Dekohärenz = wechselseitige dynamischer "Unsichtbarkeit" von "Zweigen") oder Interpretationen bzw. Worte ("Welten", "Zweige", "Verzweigungen", ...).
|
Hm, also bist du der Ansicht, daß sich Ensembleinterpretation und Viele-Welten-Interpretation im wesentlichen durch den Gebrauch von Worten unterscheiden?
Einen Kollaps gibt es in der Ensemble Interpretation jedenfalls auch nicht (und m.E. in keiner ernstzunehmenden Formulierung der QM). Und wenn es sich bei dem Rest um Theoreme der Everettschen Formulierung handelt, dann sind sie auch Theoreme der Ensembleinterpretation, denn diese verwendet dieselben Axiome, die du aufgezählt hast. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Aug 2015 21:34 Titel: TomS Verfasst am: 25. Aug 2015 21:34 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Axiome:
1) Quantum states are represented by unit vectors in a separable Hilbert space.
2) Quantum states evolve in time according to the Schrödinger equation.
That's it!
|
Die bedingungslose Gültigkeit (insbesondere ohne Ausnahme für den Meßprozeß) dieser beiden Axiome stellt die Ensembleinterpretation a la Ballentine ja auch voran. Die eigentlich problematischen Aspekte der Interpretation löst sie damit allerdings auch nicht. Sie hat allerdings (im Gegensatz zur Kollapsinterpretation) den Vorteil nicht zu völlig absurden Ergebnissen zu kommen. |
Ok, passt.
| index_razor hat Folgendes geschrieben: | | Zitat: |
Ich würde noch hinzufügen:
0) Quantum states and their dynamics represent the behavior of physical systems
|
Das ist m.E. so nichtssagend, daß man es auch weglassen kann. (Anhänger welcher Interpretation würden die Aussage in dieser Formulierung bestreiten?) |
Nein, das ist der Kerngedanke, in dem sich die Interpretationen unterscheiden! Evtl. muss man aber noch mal präzisieren.
Anhänger der orthodoxen Interpretation müssen dieses Axiom zumindest modifizieren, indem sie "dynamics" dahingehend einschränken, dass sie zwischen unitärer Dynamik und Kollaps unterscheiden. Diese beiden Dynamiken sind wechselweise inkonsistent.
Anhänger von Quanten-Bayesianismus und ich denke auch Anhänger der KI lehnen dieses Statement ab, weil sie im Zustand keine direkte Repräsentation des physikalischen Systems sondern lediglich unserer Information über das physikalische System sehen.
Anhänger der Ensemble-Interpretation lehnen das Statement ab, da sie in dem Zustand lediglich eine Repräsentation eines Ensembles von Systemen, nicht eines einzelnen Systems sehen, d.h. letztlich, dass der Zustand gerade nicht das Verhalten eines Systems repräsentiert, sondern lediglich als Hilfsmittel dient, Erwartungswertes zu berechnen.
Während Everett also den Quantenzustand vollumfänglich real / ontologisch auffasst, sehen ihn die meisten anderen Interpretationen als reines Hilfsmittel bzw. sind diese im Kern rein epistemisch.
| index_razor hat Folgendes geschrieben: | | Die eigentliche Frage ist doch: Inwiefern "repräsentiert" eine Superposition aus toter und lebendiger Katze das physikalische System "Katze"? Ein solcher Zustand repräsentiert eben eine Katze die mit Wahrscheinlichkeit soundso tot, und mit der komplementären Wahrscheinlichkeit lebendig ist. Wie würde man diese Aussage nun experimentell prüfen? Wahrscheinlich indem man eine Reihe von Katzen nach Schrödingers Vorschrift "präpariert" und nachzählt, ob die relativen Häufigkeiten stimmen. Und da hast du nun dein Ensemble. |
Korrekt.
Dennoch besteht Everett auf der direkten Repräsentation eines einzelnen Systems durch einen Zustand.
| index_razor hat Folgendes geschrieben: | | ... denn eine einzelne Katze ist ja immer entweder tot oder lebendig ... |
Everett sieht das anders.
Er gesteht der Katze (nicht "Zweig-lokal" sondern "global") in ihrem Superpositionszustand eine reale Existenz zu. Die Grundlage für diese Behauptung ist letztlich, dass er alle Schlussfolgerungen aus der hinteren Dynamik als real akzeptiert.
| index_razor hat Folgendes geschrieben: | | Wie ergibt sich nun also aus der Wahrscheinlichkeitsamplitude, die den quantenmechanischen Zustand komplett beschreibt, die nachträgliche Sicherheit eines einzelnen Meßergebnisses bei einer konkreten Messung? |
Die Sicherheit eines Messergebnisses liegt nur "Zweig-lokal" vor. Schau dir mal bitte die (rudimentäre) Formel in meinem letzten Beitrag an; sie wird nur dann angezweifelt, wenn sie auf makroskopische Systeme angewandt wird. Angewandt auf mikroskopische Systeme glaubt man sie seit fast 100 Jahren. Warum muss die Everett-Interpretation eine Ausnahme oder Unterscheidung erklären, die sind selbst gar nicht einführt?
| index_razor hat Folgendes geschrieben: | | Inwiefern erhöht die Kenntnis des Ergebnisses dieser Messung die Information über den Zustand, die vorher bereits vollständig war? |
Ich denke, da verstehe ich dich nicht korrekt.
Die Everett Interpretation hat m.E. nur ein einziges Problem, nämlich die Ableitung der Bornschen Regel:
1) die Argumente von Everett und (heute) Wallace u.a. sind nicht unumstritten (das gesteht auch Wallace zu)
2) der "Hartle frequency operator" hilft m.E. nur bei der Ensemble-Interpretation, nicht bei Everett (da weder eine mehrfache Messung noch ein Ensemble vorliegen muss sondern die Gültigkeit bereits für eine einzelne Messung = Wechselwirkung gelten soll).
3) Gleason's Theorem besagt lediglich, dass wenn ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt wird, dieses zwingend der Bornschen Regel entsprechen muss; es besagt nicht, dass eine Wahrscheinlichkeit eingeführt werden muss.
| index_razor hat Folgendes geschrieben: | | Zitat: | Alles andere ist überflüssig (Kollaps, Projektionspostulat), sind Theoreme (Bornsche Regel, Dekohärenz = wechselseitige dynamischer "Unsichtbarkeit" von "Zweigen") oder Interpretationen bzw. Worte ("Welten", "Zweige", "Verzweigungen", ...).
|
Hm, also bist du der Ansicht, daß sich Ensembleinterpretation und Viele-Welten-Interpretation im wesentlichen durch den Gebrauch von Worten unterscheiden? |
Wenn Ballentine ebenfalls mit diesen beiden Axiomen auskommt, dann im engeren Sinne ja. Ich denke, der wesentliche Unterschied liegt jedoch in meinem Axiom (0); dieses ist jedoch nicht physikalischer bzw. mathematischer sondern metaphysischer Natur.
| index_razor hat Folgendes geschrieben: | | Einen Kollaps gibt es in der Ensemble Interpretation jedenfalls auch nicht ... |
ok
| index_razor hat Folgendes geschrieben: | | ... und m.E. in keiner ernstzunehmenden Formulierung der QM |
Starker Tobak. Damit behauptest du nichts weniger, als dass die Mehrzahl der Lehrbücher, Vorlesungen etc. auf den Müll gehören und dass die Mehrzahl der Physiker irregeleitet sind (ich stimme dir aber zu, ich halte den Kollaps für unerträglichen Murks).
| index_razor hat Folgendes geschrieben: | | Und wenn es sich bei dem Rest um Theoreme der Everettschen Formulierung handelt, dann sind sie auch Theoreme der Ensembleinterpretation, denn diese verwendet dieselben Axiome, die du aufgezählt hast. |
Ja.
Zuletzt bearbeitet von TomS am 26. Aug 2015 07:26, insgesamt einmal bearbeitet |
|
 |
Herbst
Anmeldungsdatum: 08.08.2015
Beiträge: 7
|
 Herbst Verfasst am: 25. Aug 2015 22:18 Titel: Herbst Verfasst am: 25. Aug 2015 22:18 Titel: |
 |
|
| Zitat: | | Ja, sind sie tatsächlich ausreichend? |
Setzt die EI mehr voraus als die VWI? Außer dass einige Formulierungen ggf. geändert werden müssen wie bei 0).
| Zitat: | | Dazu benötigt man keine Interpretation, die o.g. Axiome sowie ein konkreter Hamiltonoperator sind ausreichend. |
Für die Dekohärenz habe ich keine Interpretation vorausgesetzt. Die EI widerspricht der Dekohärenz nicht, also deswegen "an einem Ensemble [...] erklären". Und das halt anschaulich(er) (als bei der VWI [wie immer m.M.n.]).
| Zitat: | | Verwendet man den "Hartle frequency operator"? |
Ja, denke schon. Habe eine >>Herleitung<< gelesen, die aber diesen Begriff nicht verwendet hat. Habe jetzt eben sehr kurz nachgeschaut und glaube, dass die gleiche oder ganz ähnliche Argumentation verwendet wird. Wenn du an dieser Sache was auszusetzen hast, immer her damit. Ich setze mich vergleichsweise noch nicht lange mit den Interpretationen auseinander (bin ja noch Student) und deswegen muss ich noch (viel) lernen. :-)
| Zitat: | | Gerade diese Kritik kann ich nicht nachvollziehen. [...] Dekohärenz, d.h. in der dynamischen Unterdrückung der Sichtbarkeit anderer "Zweig |
Die Dekohärenz beschreibt doch nur die Diagonalisierung der Dichtematrix, das was danach kommt (Messung, ...), ist Interpretation. Aber nur die VWI sagt, dass alle Möglichkeiten realisiert werden, nur eben nicht wahrgenommen werden können, also kein Phänomen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Aug 2015 22:57 Titel: TomS Verfasst am: 25. Aug 2015 22:57 Titel: |
 |
|
| Herbst hat Folgendes geschrieben: | | Wenn du an dieser Sache was auszusetzen hast, immer her damit. |
Ich habe an den Theoremen nichts auszusetzen.
| Herbst hat Folgendes geschrieben: | | Ich setze mich vergleichsweise noch nicht lange mit den Interpretationen auseinander |
Ich habe nie selbst in diesem Bereich gearbeitet und bin daher nicht wirklich besser dran als du.
| Herbst hat Folgendes geschrieben: | | Zitat: | | Gerade diese Kritik kann ich nicht nachvollziehen. [...] Dekohärenz, d.h. in der dynamischen Unterdrückung der Sichtbarkeit anderer "Zweig |
Die Dekohärenz beschreibt doch nur die Diagonalisierung der Dichtematrix, das was danach kommt (Messung, ...), ist Interpretation. Aber nur die VWI sagt, dass alle Möglichkeiten realisiert werden, nur eben nicht wahrgenommen werden können, also kein Phänomen. |
Jein.
Die VWI nimmt letztlich das Ergebnis der unitären Dynamik immer, d.h. ohne Ausnahme als "für ein einzelnes System real existent" an. Daraus folgen nun beobachtbare Phänomene:
Im Falle des Doppelspalts ist die destruktive Interferenz eine spezifisch quantenmechanische Vorhesage und ein real beobachtbares Phänomen (genauso wie die konstruktive Interferenz).
Im Falle der Dekohärenz ist die dynamische Unterdrückung der wechselseitigen Sichtbarkeit der "Zweige" ebenfalls eine spezifisch quantenmechanische Vorhersage und daher ein real beobachtbares Phänomen.
Wenn eine Theorie vorhersagt, dass man ein aus anderen Gründen erwartetes Phänomen nicht beobachtet, dann ist das auch eine Vorhersage, und die nicht-Beobachtung des einen Phänomens ist auch eine Beobachtung (Verletzung der Ladungserhaltung, neutrinoloser doppelter Betazerfall, freie Farbladungen, ..., no-cloning theorem, ...) Was ich damit sagen will ist, dass wir uns nicht beliebig aussuchen können, was ein Phänomen ist und was nicht. Wenn wir das tun, bewegen wir uns bereits auf der Ebene der Interpretation oder der Philosophie. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Aug 2015 20:16 Titel: index_razor Verfasst am: 26. Aug 2015 20:16 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: | | Zitat: |
Ich würde noch hinzufügen:
0) Quantum states and their dynamics represent the behavior of physical systems
|
Das ist m.E. so nichtssagend, daß man es auch weglassen kann. (Anhänger welcher Interpretation würden die Aussage in dieser Formulierung bestreiten?) |
Anhänger der orthodoxen Interpretation müssen dieses Axiom zumindest modifizieren, indem sie "dynamics" dahingehend einschränken, dass sie zwischen unitärer Dynamik und Kollaps unterscheiden. Diese beiden Dynamiken sind wechselweise inkonsistent.
Anhänger von Quanten-Bayesianismus und ich denke auch Anhänger der KI lehnen dieses Statement ab, weil sie im Zustand keine direkte Repräsentation des physikalischen Systems sondern lediglich unserer Information über das physikalische System sehen.
Anhänger der Ensemble-Interpretation lehnen das Statement ab, da sie in dem Zustand lediglich eine Repräsentation eines Ensembles von Systemen, nicht eines einzelnen Systems sehen.
|
Ich verstehe zwar (denke ich zumindest) was du meinst, glaube aber immer noch nicht, daß dieses Axiom die Unterschiede der Interpretationen gut ausdrückt. Ich sehe den Grund wie gesagt unter anderem darin, daß keine Interpretation schlüssig erklären kann, wie eine Wahrscheinlichkeitsamplitude individuelle Systeme repräsentieren kann. (siehe weiter unten). Ich sehe es auch so, daß eher die KI, nicht die Everettsche Interpretation, diese System-Zustand-Korrespondenz am wörtlichsten nimmt. Sie muß dafür halt leugnen, daß bestimmte Superpositionen (tot-lebendig) existieren, da sie sich nicht in den Phänomenen widerspiegeln. Mit den bekannten unhaltbaren Konsequenzen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Die eigentliche Frage ist doch: Inwiefern "repräsentiert" eine Superposition aus toter und lebendiger Katze das physikalische System "Katze"? Ein solcher Zustand repräsentiert eben eine Katze die mit Wahrscheinlichkeit soundso tot, und mit der komplementären Wahrscheinlichkeit lebendig ist. Wie würde man diese Aussage nun experimentell prüfen? Wahrscheinlich indem man eine Reihe von Katzen nach Schrödingers Vorschrift "präpariert" und nachzählt, ob die relativen Häufigkeiten stimmen. Und da hast du nun dein Ensemble. |
Korrekt. Dennoch besteht Everett auf der direkten Repräsentation eines einzelnen Systems durch einen Zustand.
|
Dann muß ja ein einzelnes System irgendwie alle durch den Zustand beschriebenen Zweige beinhalten. Das grenzt schon mal stark an rhetorische Spielerei. Denn das eigentliche Problem ist immer noch unbeantwortet und lautet umformuliert in die Sprache der Everettschen Interpretation: Wie ergibt sich aus dem Zustand in welchem Zweig man sich nach einer Messung wiederfinden wird. Die Situation ist exakt genauso unbefriedigend wie in der Ensembleinterpretation. Da kann ich nämlich auch sagen: Das System, das sei eigentlich nicht die Katze, sondern ein Ensemble aus identisch präparierten Katzen. Man weiß eben nur vor der Messung nicht, mit welchem Vertreter des Ensembles man es zu tun hat. Es gibt keinen "Mikrozustand" der die Ensemblevertreter unterscheidet.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | ... denn eine einzelne Katze ist ja immer entweder tot oder lebendig ... |
Everett sieht das anders. Er gesteht der Katze (nicht"Zweig-lokal" sondern "global") in ihrem Superpositionszustand eine reale Existenz zu. Die Grundlage für diese Behauptung ist letztlich, dass er alle Schlussfolgerungen aus der hinteren Dynamik als real akzeptiert.
|
Meine Aussage ist so zu verstehen, daß das was beobachtet wird entweder die Eigenschaft "tot" oder "lebendig" ist, nichts anderes. Es handelt sich also um die bekannte Feststellung, daß jede einzelne Messung als Ergebnis einen einzigen konkreten Meßwert aus dem Spektrum irgendeines Operators hat. In Everetts eigenen Worten:
"Consider any measuring apparatus interacting with any object system. As a result of the interaction the state of the measuring apparatus is no longer capable of independent definition. [...] It seems as if nothing can ever be settled by such a measurement.
This indifferent behavior seems to be quite at variance with our observations, since physical objects always appear to us to have definite positions." (H. Everett, Rev. Mod. Phys., 29 (1957))
Ich erhalte niemals mehr als einen Meßwert oder eine Superposition von Meßwerten. Die Grundfrage seit den Anfängen der Quantenmechanik lautet nun: Wie läßt sich die Tatsache deuten, daß eine vollständige Beschreibung des Zustands nur Wahrscheinlichkeitsaussagen über das Auftreten dieser Meßergebnisse erlaubt und wie wird aus einer Wahrscheinlichkeit ein Meßwert? Die Ensembleinterpretation nimmt im wesentlichen hin, keine tiefsinnige Antwort vorweisen zu können. (Die Interpretation, daß sich der Zustand auf ein Ensemble bezieht und nicht auf ein Einzelsystem besagt nicht viel anderes, als daß mehr als Wahrscheinlichkeitsaussagen nun mal nicht drin sind.) Everett versucht jetzt irgendwie mehr zu erreichen, mir ist nur nicht klar was er meint mehr erreicht zu haben.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Wie ergibt sich nun also aus der Wahrscheinlichkeitsamplitude, die den quantenmechanischen Zustand komplett beschreibt, die nachträgliche Sicherheit eines einzelnen Meßergebnisses bei einer konkreten Messung? |
Die Sicherheit eines Messergebnisses liegt nur "Zweig-lokal" vor. Schau dir mal bitte die (rudimentäre) Formel in meinem letzten Beitrag an; sie wird nur dann angezweifelt, wenn sie auf makroskopische Systeme angewandt wird. Angewandt auf mikroskopische Systeme glaubt man sie seit fast 100 Jahren. Warum muss die Everett-Interpretation eine Ausnahme oder Unterscheidung erklären, die sind selbst gar nicht einführt?
|
Ich behaupte doch nicht, sie müßte es. Das Problem ist nicht die Abgrenzung zwischen mikroskopischen und makroskopischen Systemen. Die Anwendung dieser Formel auf makroskopische Systeme widerspricht nur am auffälligsten unserer Intuition. Aber für mikroskopische Systeme ist die Lage nicht weniger undurchsichtig. Das ändert natürlich nichts daran, daß man dem Formalismus vollständig glaubt. Schließlich kann man seine Konsequenzen experimentell überprüfen. Wenn die QM korrekt ist, bleibt uns nichts anderes übrig als diese Formel für alle Systeme, mikroskopisch und makroskopisch, zu glauben, denn es gibt gar keinen prinzipiellen, sondern allenfalls einen graduellen Unterschied zwischen diesen beiden Fällen.
Die Erklärung der Sicherheit als "zweiglokal" löst das Problem nicht, sondern formuliert es nur um. Ich möchte gerade wissen, wie aus dem Formalismus der QM eine "zweiglokale" Phänomenologie ergibt. Zu postulieren, daß es noch andere Zweige gibt, verfehlt das Thema genauso wie wenn ein Vertreter der Ensembleinterpretation behaupten würde die Sicherheit eines gegebenen Meßwertes läge nur für einige Mitglieder des Ensembles vor und für andere nicht. Was unterscheidet die Ensemblemitglieder/Zweige voneinander? Lediglich die Ergebnisse von Einzelmessungen. Das sind Unterschiede die also nicht durch den Zustand beschrieben werden können. Das ist genau das Problem mit dem man angefangen hat.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Inwiefern erhöht die Kenntnis des Ergebnisses dieser Messung die Information über den Zustand, die vorher bereits vollständig war? |
Ich denke, da verstehe ich dich nicht korrekt.
|
Ich meine folgendes: In den üblichen statistischen Ensembles der klassischen Physik sind einige Observablen wie der Aufenthaltsort aller Teilchen unbestimmt. Ich kann allerdings die Positionen messen und dadurch meine Kenntnis über den Mikrozustand prinzipiell beliebig erhöhen. In der QM kann ich das nicht. Trotzdem erfahre ich ja durch die Messung irgendetwas über das System. Nur kann ich dieses Ergebnis nicht sinnvoll in die Beschreibung des Zustands einfügen. Dieser Gedankengang hängt, denke ich, historisch mit Kollapsinterpretation zusammen. Man versuchte eben irgendwie einen Spagat zwischen der vollständigen Beschreibung eines einzelnen Systems durch den Zustandsvektor und dem Meßprozeß hinzubekommen.
| Zitat: |
Die Everett Interpretation hat m.E. nur ein einziges Problem, nämlich die Ableitung der Bornschen Regel:
1) die Argumente von Everett und (heute) Wallace u.a. sind nicht unumstritten (das gesteht auch Wallace zu)
2) der "Hartle frequency operator" hilft m.E. nur bei der Ensemble-Interpretation, nicht bei Everett (da weder eine mehrfache Messung noch ein Ensemble vorliegen muss sondern die Gültigkeit bereits für eine einzelne Messung = Wechselwirkung gelten soll).
3) Gleason's Theorem besagt lediglich, dass wenn ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt wird, dieses zwingend der Bornschen Regel entsprechen muss; es besagt nicht, dass eine Wahrscheinlichkeit eingeführt werden muss.
|
Ich sehe keine logischen Probleme mit dieser Interpretation. Wenn sie dieselben Axiome benutzt, wie bspw. die Ensembleinterpretation lassen sich auch dieselben Theoreme ableiten. Sie liefert allerdings genausowenig wie die Ensembleinterpretation eine befriedigende (einige würden sagen "realistische") Interpretation des Zustandsvektors oder eine Auflösung des Meßproblems.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zitat: | Alles andere ist überflüssig (Kollaps, Projektionspostulat), sind Theoreme (Bornsche Regel, Dekohärenz = wechselseitige dynamischer "Unsichtbarkeit" von "Zweigen") oder Interpretationen bzw. Worte ("Welten", "Zweige", "Verzweigungen", ...).
|
Hm, also bist du der Ansicht, daß sich Ensembleinterpretation und Viele-Welten-Interpretation im wesentlichen durch den Gebrauch von Worten unterscheiden? |
Wenn Ballentine ebenfalls mit diesen beiden Axiomen auskommt, dann im engeren Sinne ja. Ich denke, der wesentliche Unterschied liegt jedoch in meinem Axiom (0); dieses ist jedoch nicht physikalischer bzw. mathematischer sondern metaphysischer Natur.
|
Volle Zustimmung, daß es sich nicht um mathematische oder physikalische Unterschiede handelt. (Meine Vorbehalte bzgl. der Formulierung deines Axioms hatte ich ja schon geäußert.) Wenn beide Formulierungen Axiome verwendeten, die nicht äquivalent sind, dann wäre es ja auch nicht richtig von Interpretationen zu sprechen, sondern von verschiedenen Theorien. Es geht einzig und allein darum, wie der Zustand zu deuten ist.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | ... und m.E. in keiner ernstzunehmenden Formulierung der QM |
Starker Tobak. Damit behauptest du nichts weniger, als dass die Mehrzahl der Lehrbücher, Vorlesungen etc. auf den Müll gehören und dass die Mehrzahl der Physiker irregeleitet sind (ich stimme dir aber zu, ich halte den Kollaps für unerträglichen Murks).
|
Die Aussage, daß ("unmittelbar"?) nach einer Messung ein Eigenzustand der vermessenen Observable vorliegt, halte ich in der Tat für vollkommen irregeleitet. Komischerweise wird dieses Axiom zwar oft gepredigt, aber irgendwie selten wirklich angewendet. Nicht zuletzt wahrscheinlich deshalb, weil bei realen Messungen seine Anwendung völlig unklar ist. Im Extremfall ist das Objekt, z.B. ein Photon, dessen Zustand man vermessen hat, schlicht absorbiert worden. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Aug 2015 17:30 Titel: TomS Verfasst am: 27. Aug 2015 17:30 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ich verstehe zwar (denke ich zumindest) was du meinst, glaube aber immer noch nicht, daß dieses Axiom die Unterschiede der Interpretationen gut ausdrückt. Ich sehe den Grund wie gesagt unter anderem darin, daß keine Interpretation schlüssig erklären kann, wie eine Wahrscheinlichkeitsamplitude individuelle Systeme repräsentieren kann. |
Das sind zwei verschiedene Dinge.
1) Der wesentliche Kernpunkt der Everettschen Interpretation ist, dass diese behauptet , dass ein mathematischer Quantenzustand und dessen Dynamik gemäß der Axiome der QM den tatsächlichen Zustand und die tatsächliche Dynamik des einen real existierenden physikalischen Systems repräsentiert, dass also eine Art Isomorphie vorliegt. Dies unterscheidet die Everettschen Interpretation von allen anderen Interpretationen.
(Die Kopenhagen- / orthodoxe I. kann dies nicht behaupten, da sie entweder den Kollaps außen vorlassen muss, was bedeutet, dass nicht alle mathematischen Strukturen der QM ihre isomorphen Entsprechungen in der Natur haben; oder da sie den Kollaps als real existierend ansehen müsste, was sofort zu einer Inkonsistenz mit der unitären Dynamik führt.
Die Ensemble-I. will dies nicht, da sie keinen Realitätsanspruch erhebt. Andere Interpretationen wie Quanten-Bayesianismus usw. wollen dies ebenfalls nicht, da sie dem Quantenzustand keine ontologische Bedeutung zuschreiben.)
Es ist wichtig, diesen philosophischen Anspruch zu verstehen.
2) Der zweite Knackpunkt für die Everettschen I. ist, dass es tatsächlich noch unklar ist, ob sie das Auftreten von Wahrscheinlichkeiten schlüssig erklären kann (Wallace; habe ich oben so geschrieben). Zur Erinnerung: es ist beweisbar, dass WENN ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt werden soll, dass dies DANN der (verallgemeinerten) Bornschen Regel entsprechen muss (Gleason); es ist NICHT beweisbar, dass ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt werden MUSS.
(1) unterscheidet die Everettsche I. von allen anderen Interpretationen. (2) ist das zentrale Problem Everettschen I.
| index_razor hat Folgendes geschrieben: | | Die eigentliche Frage ist doch: Inwiefern "repräsentiert" eine Superposition aus toter und lebendiger Katze das physikalische System "Katze"? |
Die Everettsche I. GLAUBT im Sinne einer philosophischen Überzeugung, dass dies so IST: Der Quantenzustand ist strukturell isomorph zu einer realen Katze, d.h. letztere IST REAL in einer derartigen Superposition.
Dies, also (1) ist der einzige, wesentliche Grund, warum man die Everettsche I. ablehnen kann. (2) ist KEIN derartiger Grund, denn (2) ist letztlich die Aufforderung zu einem mathemastischen Forschungsprogramm, das Auftreten von Wahrscheinlichkeiten, die Bornsche Regel etc. als Theoreme zu beweisen.
Letzteres ist kein Thema für die Ensemble-I., da diese den o.g. ontologischen Anspruch nicht hat. Sie muss nicht erklären, warum Wahrscheinlichkeiten auftreten.
| index_razor hat Folgendes geschrieben: | | Ein solcher Zustand repräsentiert eben eine Katze die mit Wahrscheinlichkeit soundso tot, und mit der komplementären Wahrscheinlichkeit lebendig ist. |
Nicht im Sinne von Everett.
| index_razor hat Folgendes geschrieben: | | Dann muß ja ein einzelnes System irgendwie alle durch den Zustand beschriebenen Zweige beinhalten. |
Ja, gem. Everett ist das so.
| index_razor hat Folgendes geschrieben: | | Das grenzt schon mal stark an rhetorische Spielerei. |
Nein.
Es ist eine ontologische Zumutung, aber es ist rhetorisch, logisch usw. völlig trivial.
| index_razor hat Folgendes geschrieben: | | Denn das eigentliche Problem ist immer noch unbeantwortet und lautet umformuliert in die Sprache der Everettschen Interpretation: Wie ergibt sich aus dem Zustand in welchem Zweig man sich nach einer Messung wiederfinden wird. |
Ja.
S.o. (2) ist das zentrale Problem Everettschen I.
| index_razor hat Folgendes geschrieben: | | Die Situation ist exakt genauso unbefriedigend wie in der Ensembleinterpretation. |
Das kommt auf deinen Anspruch an.
Wenn du einen ontologischen Anspruch an die Quantenmechanik hast, dann löst die Everettsche I. genau dieses Problem. Sie bietet eine logisch konsistente Axiomatik und Ontologie an. Die Ensemble-I. kann dies nicht; sie bietet KEINE Ontologie bzgl. eines einzelnen Systems an, d.h. sie bleibt rein phänomenologisch.
Klar, warum die MWI gerade in der Quantenkosmologie so beliebt ist?
| index_razor hat Folgendes geschrieben: | Die Grundfrage seit den Anfängen der Quantenmechanik lautet nun: Wie läßt sich die Tatsache deuten, daß eine vollständige Beschreibung des Zustands nur Wahrscheinlichkeitsaussagen über das Auftreten dieser Meßergebnisse erlaubt und wie wird aus einer Wahrscheinlichkeit ein Meßwert?
…
Everett versucht jetzt irgendwie mehr zu erreichen, mir ist nur nicht klar was er meint mehr erreicht zu haben. |
Everett erreicht zusammen mit der später entwickelten Dekohärenz deutlich mehr. Letztere liefert dir gerade die „wechselweise unsichtbaren Zweige“; Zurek spricht von „einselection“ = environment-induced superselection“. Alles was man nun noch annehmen muss ist, dass diese „wechselweise unsichtbaren Zweige“ real existent sind und bleiben. Das ist logisch konsistent möglich.
| index_razor hat Folgendes geschrieben: | | Ich möchte gerade wissen, wie aus dem Formalismus der QM eine "zweiglokale" Phänomenologie ergibt. Zu postulieren, daß es noch andere Zweige gibt, verfehlt das Thema … |
Korrektur: die Everett-I. postuliert diese Zweige nicht, sie akzeptiert ihre Realität als Folgerung des Formalismus. Das ist mathematisch kein Unterschied, jedoch philosophisch bzw. axiomatisch ein ganz erheblicher. Die Everett-I. ist logisch konsistent, axiomatisch sparsam (im Sinne von Ockham).
| index_razor hat Folgendes geschrieben: | | Was unterscheidet die Zweige voneinander? Lediglich die Ergebnisse von Einzelmessungen. Das sind Unterschiede die also nicht durch den Zustand beschrieben werden können. Das ist genau das Problem mit dem man angefangen hat. |
Doch, das hat bereits Everett diskutiert; deshalb hieß sein Ansatz ja ursprünglich „relative state interpretation“.
Ich denke nach wie vor, dass das wesentliche Problem das von mir o.g. (1) ist.
Ich zeige das nochmal anhand des Stern-Gerlach Experimentes: gegeben sei ein Zustand im Produkthilbertraum „Quantensystem“ * „Messgerät plus Beobachter“ * Umgebung“:
(a|up> + b|down>) |NEUTRAL> |…>
Die Wechselwirkung mit dem Messgerät sowie der Umgebung führt zu einer „Zweigstruktur“ im Sinne von
(a|up> |UP> |…> + b|down> |DOWN> |…> + suppressed, non-diag. terms
Eine naive Abzählung von Zweigen ergibt 2. Eine (wiederholte) Messung liefert eine Häufigkeitsverteilung entsprechend |a|² bzw. |b|², die einer naiven Annahme von ½ widerspricht. Die Frage, die sich hinter (1) verbirgt ist folgende: warum erlebe ich Zweig-lokal eine |a|² sowie |b|² entsprechende Häufigkeitsverteilung? wie motiviere ich die Einführung einer Wahrscheinlichkeit in den Formalismus? Ich bin ehrlich, die habe die (nicht unumstrittenen Argumente) bisher nicht wirklich verstanden. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Aug 2015 10:37 Titel: index_razor Verfasst am: 29. Aug 2015 10:37 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Ich verstehe zwar (denke ich zumindest) was du meinst, glaube aber immer noch nicht, daß dieses Axiom die Unterschiede der Interpretationen gut ausdrückt. Ich sehe den Grund wie gesagt unter anderem darin, daß keine Interpretation schlüssig erklären kann, wie eine Wahrscheinlichkeitsamplitude individuelle Systeme repräsentieren kann. |
Das sind zwei verschiedene Dinge.
1) Der wesentliche Kernpunkt der Everettschen Interpretation ist, dass diese behauptet , dass ein mathematischer Quantenzustand und dessen Dynamik gemäß der Axiome der QM den tatsächlichen Zustand und die tatsächliche Dynamik des einen real existierenden physikalischen Systems repräsentiert, dass also eine Art Isomorphie vorliegt. Dies unterscheidet die Everettschen Interpretation von allen anderen Interpretationen.
(Die Kopenhagen- / orthodoxe I. kann dies nicht behaupten, da sie entweder den Kollaps außen vorlassen muss, was bedeutet, dass nicht alle mathematischen Strukturen der QM ihre isomorphen Entsprechungen in der Natur haben; oder da sie den Kollaps als real existierend ansehen müsste, was sofort zu einer Inkonsistenz mit der unitären Dynamik führt.
Die Ensemble-I. will dies nicht, da sie keinen Realitätsanspruch erhebt. Andere Interpretationen wie Quanten-Bayesianismus usw. wollen dies ebenfalls nicht, da sie dem Quantenzustand keine ontologische Bedeutung zuschreiben.)
Es ist wichtig, diesen philosophischen Anspruch zu verstehen.
|
Ich verstehe diesen philosophischen Anspruch durchaus und teile ihn auch. Ich meine aber, daß die MWI, trotz des größeren Anspruchs, in dieser Hinsicht genauso wenig leistet, wie die Ensembleinterpretation. (Egal, ob letztere diesen Anspruch überhaupt hat oder nicht.)
| Zitat: |
2) Der zweite Knackpunkt für die Everettschen I. ist, dass es tatsächlich noch unklar ist, ob sie das Auftreten von Wahrscheinlichkeiten schlüssig erklären kann (Wallace; habe ich oben so geschrieben). Zur Erinnerung: es ist beweisbar, dass WENN ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt werden soll, dass dies DANN der (verallgemeinerten) Bornschen Regel entsprechen muss (Gleason); es ist NICHT beweisbar, dass ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt werden MUSS.
|
Ich sehe kein Problem in der Unmöglichkeit zu beweisen, daß man irgendwo ein Wahrscheinlichkeitsmaß einführen MUSS. Wäre es eins, wäre es wohl ohnehin unlösbar. Aber selbst wenn ich das Auftreten von Wahrscheinlichkeiten einfach hinnehme, existieren für mich noch genug andere Probleme.
| Zitat: |
(1) unterscheidet die Everettsche I. von allen anderen Interpretationen. (2) ist das zentrale Problem Everettschen I.
|
Das mag ja sein. Ich beurteile die Interpretation aber nicht nach ihren philosophischen Ansprüchen, sondern danach wie sie ihnen gerecht wird. Zumindest versuche ich das. Kann natürlich passieren, daß ich der Everettschen Interpretation unrecht tue. Ich sehe aber keinerlei ontologischen, philosophischen, oder sonstigen Vorsprung vor der Ensembleinterpretation. Die technischen Probleme innerhalb der MWI interessieren mich natürlich erst, wenn ich überzeugt bin, daß sie die philosophischen Ansprüche erfüllt, die ich teile und nicht schlimmere Probleme erzeugt.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Die eigentliche Frage ist doch: Inwiefern "repräsentiert" eine Superposition aus toter und lebendiger Katze das physikalische System "Katze"? |
Die Everettsche I. GLAUBT im Sinne einer philosophischen Überzeugung, dass dies so IST: Der Quantenzustand ist strukturell isomorph zu einer realen Katze, d.h. letztere IST REAL in einer derartigen Superposition.
|
Das ist genau das, was ich als philosophischen Taschenspielertrick sehe. (Ich versuche es nochmal unten zu begründen.)
| Zitat: |
Dies, also (1) ist der einzige, wesentliche Grund, warum man die Everettsche I. ablehnen kann. (2) ist KEIN derartiger Grund, denn (2) ist letztlich die Aufforderung zu einem mathemastischen Forschungsprogramm, das Auftreten von Wahrscheinlichkeiten, die Bornsche Regel etc. als Theoreme zu beweisen.
|
Haben wir uns mißverstanden? Ich würde keine Interpretation ablehnen, weil sie gewisse philosophische Ansprüche hat, sondern weil ich meine, daß sie diese nicht erfüllt, und eine Lösung nur mit viel Brimborium vortäuscht. Mit (2) habe ich, wie gesagt, überhaupt kein Problem.
| Zitat: |
Letzteres ist kein Thema für die Ensemble-I., da diese den o.g. ontologischen Anspruch nicht hat. Sie muss nicht erklären, warum Wahrscheinlichkeiten auftreten.
|
Verstehe ich nicht. Wieso muß ich das Auftreten von Wahrscheinlichkeiten genau dann erklären, wenn ich irgendwelche ontologischen Ansprüche habe? Warum Wahrscheinlichkeiten auftreten, ist allerdings auch einfach nicht die Frage um die es geht. Das Problem ist wie Meßwerte realisiert werden, bzw, wie man den Meßprozeß realistisch erklären kann. Die Ensembleinterpretation erklärt den Meßprozeß ganz einfach mit Hilfe von Wahrscheinlichkeiten: ~|zerfall>|tot> + |intakt>|lebendig> bedeutet: "Mit 50 % Wahrscheinlichkeit ist das Isotop zerfallen und die Katze tot, mit 50 % Wahrscheinlichkeit ist das Isotop nicht zerfallen und die Katze lebt noch. Andere Möglichkeiten gibt es nicht." Die Aussage stimmt zwar, und beschreibt eine simple Korrelation von Ereignissen, nur hat sie für eine vollständige Beschreibung des Vorgangs einen etwas dürftigen Bezug zur Realität der tatsächlich beobachteten Phänomene. Ich will nicht nur wissen, mit welcher Wahrscheinlichkeit ein Ereignis, welches ich beobachtet habe, vorher hätte eintreten können. Ich will wissen, warum es eintritt. Also wenn möglich eine realistische Erklärung für den Meßwert. Apodiktische Glaubensbekenntnisse wie "Der Zustand ist strukturell isomorph zum System." nehmen dieses Problem nicht mal ernst, fürchte ich.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ein solcher Zustand repräsentiert eben eine Katze die mit Wahrscheinlichkeit soundso tot, und mit der komplementären Wahrscheinlichkeit lebendig ist. |
Nicht im Sinne von Everett.
|
Er repräsentiert eine Katze, die aus einem toten und einem lebendigen Katzenteilzweig besteht. Was wissen wir quantitativ über diese Zweige? Jeder davon hat das "Maß" (oder "Gewicht") 1/2. Das ist kein anderer "Sinn", das ist lediglich ein anderer, ziemlich obskurer, Jargon.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Das grenzt schon mal stark an rhetorische Spielerei. |
Nein.
Es ist eine ontologische Zumutung, aber es ist rhetorisch, logisch usw. völlig trivial.
|
Ich sage auch nicht, daß es nicht trivial ist. Es ist mir eher zu trivial. Der Punkt ist immer noch eine gewisse Diskrepanz zwischen Phänomenen und Zustandsbeschreibung. Zu den Phänomenen gehört: Das Ergebnis einer Messung liefert genau einen Eigenwert. Aus dem Zustand, welcher die Phänomene vollständig beschreibt, ergeben sich aber lediglich Wahrscheinlichkeiten (oder "Maße") für das Auftreten jedes Eigenwertes.
Einfach den Begriff des "Systems" so zu erweitern, daß er deckungsgleich mit der im Zustand verpackten Information ist, aber dabei das Problem zu ignorieren, wie sich aus diesem Zustand konkrete Phänomene ergeben, ist pure Rhetorik und schlechte Philosophie. Die Ensembleinterpretation kann denselben Trick vollführen: System = Ensemble. Fertig. Damit ist offenbar eine 1-zu-1-Zuordnung von System und Zustand hergestellt, denn der Zustand beschreibt ein Ensemble. Wie sich aus dem Zustand nun konkrete Meßergebnisse ergeben, weiß man aber immer noch nicht. Genauso ist es bei Everett. Der Zustand beschreibt halt alle Zweige, schön und gut. Wieso scheinen nun die Phänomene genau einen Pfad durch diese Zweige auszuzeichnen? (Zur möglichen Antwort "Dekohärenz" komme ich weiter unten noch.)
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Denn das eigentliche Problem ist immer noch unbeantwortet und lautet umformuliert in die Sprache der Everettschen Interpretation: Wie ergibt sich aus dem Zustand in welchem Zweig man sich nach einer Messung wiederfinden wird. |
Ja.
S.o. (2) ist das zentrale Problem Everettschen I.
|
Das von mir formulierte Problem hat mit (2) aber nichts zu tun.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Die Situation ist exakt genauso unbefriedigend wie in der Ensembleinterpretation. |
Das kommt auf deinen Anspruch an.
Wenn du einen ontologischen Anspruch an die Quantenmechanik hast, dann löst die Everettsche I. genau dieses Problem.
|
Ich habe noch mehr Ansprüche. Ich will nicht nur irgendeine Ontologie herbeidefiniert bekommen, sondern eine mit der man das Meßproblem realistisch erklären kann. Und genau das leistet die MWI m.E. nicht. Ansonsten erkläre mir, wieso "System = Ensemble" das Problem nicht genauso löst. Es gibt keine klassischen Katzen. Es gibt nur Katzenensembles. Das hat natürlich mit der geforderten Erklärung des Meßproblems überhaupt nichts zu tun. Es kann natürlich sein, daß ich Pech habe und meine Ansprüche sich nicht erfüllen lassen. Dann bietet mir die MWI aber nichts, was mir die Ensembleinterpretation nicht mit viel mehr Verständlichkeit auch erklären könnte.
| Zitat: |
Sie bietet eine logisch konsistente Axiomatik und Ontologie an. Die Ensemble-I. kann dies nicht; sie bietet KEINE Ontologie bzgl. eines einzelnen Systems an, d.h. sie bleibt rein phänomenologisch.
|
Warum ist System = Ensemble keine Ontologie, System = Menge aller Zweige aber schon?
| Zitat: |
Klar, warum die MWI gerade in der Quantenkosmologie so beliebt ist?
|
Nein, bis jetzt ist mir überhaupt nicht klar, warum die MWI bei irgendwem beliebt ist.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Die Grundfrage seit den Anfängen der Quantenmechanik lautet nun: Wie läßt sich die Tatsache deuten, daß eine vollständige Beschreibung des Zustands nur Wahrscheinlichkeitsaussagen über das Auftreten dieser Meßergebnisse erlaubt und wie wird aus einer Wahrscheinlichkeit ein Meßwert?
…
Everett versucht jetzt irgendwie mehr zu erreichen, mir ist nur nicht klar was er meint mehr erreicht zu haben. |
Everett erreicht zusammen mit der später entwickelten Dekohärenz deutlich mehr. Letztere liefert dir gerade die „wechselweise unsichtbaren Zweige“; Zurek spricht von „einselection“ = environment-induced superselection“.
|
Die Heranziehung von Dekohärenz als Grundlage für die Zweigstruktur erscheint mir im Hinblick auf die philosophischen Ansprüche, die du formulierst völlig unzureichend. Denn sie existiert ja nicht in isolierten Systemen, Everetts Viele Welten aber ja angeblich schon. Wenn ich eine statistisch unbestimmte Wechselwirkung mit der Umgebung bräuchte, damit Zweige überhaupt entstehen, existierten keine Zweige im Universum, denn dieses hat keine Umgebung, mit der es wechselwirken kann. Die Zweige wären dann also kein fundamentales Konzept, sondern ein thermodynamisches.
| Zitat: |
Alles was man nun noch annehmen muss ist, dass diese „wechselweise unsichtbaren Zweige“ real existent sind und bleiben. Das ist logisch konsistent möglich.
|
Was soll das für ein Argument sein? Viele Annahmen sind logisch konsistent möglich, z.B. Solipsismus oder die Existenz unsichtbarer Einhörner in Paralleluniversen. Die Kunst ist nicht eine logisch konsistent mögliche, sondern eine möglichst realistische Ontologie zu finden, wie du ja ganz zu Anfang selbst geschrieben hast.
Ich habe noch andere Bedenken bezüglich dieses Vorschlags: Es wäre ja durchaus schön, wenn die reale Existenz der Zweige so ohne Probleme annehmbar wäre. Ich finde das allerdings äußerst zweifelhaft. Wenn die Zweige real wären, dann müßte ich ja zumindest jedem Zweig eindeutig einen Zustand zuordnen können. Ansonsten würde die QM keine vollständige Beschreibung der Realität liefern können. Ich denke, daß man genau diese Zuordnung aber nicht vornehmen kann (s.u.). Wenn ich recht habe, kann die MWI die reale Existenz jedes einzelnen Zweiges genauso wenig annehmen, wie die Ensembleinterpretation die Existenz der einzelnen Mitglieder des Ensembles. Konsistente Aussagen sind nur über die Gesamtheit der Zweige möglich. Was das ganze natürlich zu einem ontologischen Luftschloß macht.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ich möchte gerade wissen, wie aus dem Formalismus der QM eine "zweiglokale" Phänomenologie ergibt. Zu postulieren, daß es noch andere Zweige gibt, verfehlt das Thema … |
Korrektur: die Everett-I. postuliert diese Zweige nicht, sie akzeptiert ihre Realität als Folgerung des Formalismus. Das ist mathematisch kein Unterschied, jedoch philosophisch bzw. axiomatisch ein ganz erheblicher. Die Everett-I. ist logisch konsistent, axiomatisch sparsam (im Sinne von Ockham).
|
Was keine Folgerung ist, sollte man ehrlicherweise auch nicht als Folgerung bezeichnen. Postulat erscheint mir hier weitaus angemessener. Wenn die Realität der Zweige eine Folgerung aus dem Formalismus wäre, dann stünden alle Interpretation mit Ausnahme höchstens der Everettschen im Widerspruch zum Formalismus. Das tun sie natürlich nicht, sonst hätten wir hier nicht viel zu diskutieren. Also ist ihre Realität keine Folgerung, sondern einfach ein ontologisches Postulat. (Und mathematisch ist es natürlich schon ein Unterschied, ob ich eine Behauptung aus meinen Annahmen folgern kann oder sie postulieren muß.)
Konsistenz und axiomatische Sparsamkeit teilt sie übrigens mit der Ensembleinterpretation. Wir sollten uns darauf konzentrieren was sie auszeichnet.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Was unterscheidet die Zweige voneinander? Lediglich die Ergebnisse von Einzelmessungen. Das sind Unterschiede die also nicht durch den Zustand beschrieben werden können. Das ist genau das Problem mit dem man angefangen hat. |
Doch, das hat bereits Everett diskutiert; deshalb hieß sein Ansatz ja ursprünglich „relative state interpretation“.
|
Das überzeugt mich noch nicht. Die Beschreibung durch relative Zustände hat erstens überhaupt keine ontologischen Implikationen. Schließlich haben sie eine vollkommen einleuchtende Interpretation als Amplituden von bedingten Wahrscheinlichkeiten, die von Everett ja auch selbst geliefert wird und die von Anhängern der Ensembleinterpretation sicher auch dankend entgegengenommen wird.
Zweitens sehe ich im Augenblick auch ein logisches Problem, den Zweigen einen Produktzustand |a, relativ zu B>|B> zuzuordnen, der aus einem definitiven Beobachterzustand |B> und dem dazu relativen Systemzustand besteht, welches mir nicht lösbar erscheint. Der Endzustand ist ja völlig symmetrisch bzgl. System und Meßapparat. Der ganze Ansatz basiert ja auch darauf, daß eine Messung eine normale Wechselwirkung und ein Beobachter ein normales Quantensystem ist. Wodurch rechtfertigt sich nun die Bevorzugung von |a, relativ zu B>|B> im Gegensatz zu |a>|B relativ zu a> als Zustand des Zweiges? Man muß sich für einen entscheiden, denn beide Zustände sind nicht identisch und haben einen Überlapp. Sie können also nicht denselben und auch nicht getrennte Zweige beschreiben. Man kann höchstens postulieren, daß B, der Beobachter, derjenige ist, welcher sich im betreffenden Zweig in einem definitiven Zustand wiederfindet. Aber das ist völlig willkürlich und folgt nicht aus dem Formalismus der QM. Was wäre, wenn sich zwei Beobachter gegenseitig beobachten? Nur einer kann das Privileg haben zu definitiven Beobachtungsergebnissen gelangt zu sein. Oder wenn es sich bei den verschränkten Systemkomponenten um bspw. Spin und Impuls desselben Teilchens handelt, wie beim Stern-Gerlach-Experiment? Entstehen dann Zweige mit definitivem Spin oder mit definitiver Impulsrichtung?
(Ich habe gerade eben noch gelernt, daß eine Verallgemeinerung dieses Arguments offenbar als "Basisproblem" bekannt ist. Die einzig bekannte Lösung scheint Dekohärenz zu sein. Die greift allerdings nicht, wenn es um die fundamentale Frage der Realität der Zweige geht. Sie liefert nur die "Zweighaftigkeit" von Systemen im thermodynamischen Grenzwert. Das ist m.E. zu wenig.) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 31. Aug 2015 13:05 Titel: TomS Verfasst am: 31. Aug 2015 13:05 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Ich verstehe zwar (denke ich zumindest) was du meinst, glaube aber immer noch nicht, daß dieses Axiom die Unterschiede der Interpretationen gut ausdrückt. Ich sehe den Grund wie gesagt unter anderem darin, daß keine Interpretation schlüssig erklären kann, wie eine Wahrscheinlichkeitsamplitude individuelle Systeme repräsentieren kann. |
Das sind zwei verschiedene Dinge.
1) Der wesentliche Kernpunkt der Everettschen Interpretation ist, dass diese behauptet , dass ein mathematischer Quantenzustand und dessen Dynamik gemäß der Axiome der QM den tatsächlichen Zustand und die tatsächliche Dynamik des einen real existierenden physikalischen Systems repräsentiert, dass also eine Art Isomorphie vorliegt. Dies unterscheidet die Everettschen Interpretation von allen anderen Interpretationen.
(Die Kopenhagen- / orthodoxe I. kann dies nicht behaupten, da sie entweder den Kollaps außen vorlassen muss, was bedeutet, dass nicht alle mathematischen Strukturen der QM ihre isomorphen Entsprechungen in der Natur haben; oder da sie den Kollaps als real existierend ansehen müsste, was sofort zu einer Inkonsistenz mit der unitären Dynamik führt.
Die Ensemble-I. will dies nicht, da sie keinen Realitätsanspruch erhebt. Andere Interpretationen wie Quanten-Bayesianismus usw. wollen dies ebenfalls nicht, da sie dem Quantenzustand keine ontologische Bedeutung zuschreiben.)
Es ist wichtig, diesen philosophischen Anspruch zu verstehen. |
Ich verstehe diesen philosophischen Anspruch durchaus und teile ihn auch. Ich meine aber, daß die MWI, trotz des größeren Anspruchs, in dieser Hinsicht genauso wenig leistet, wie die Ensembleinterpretation. (Egal, ob letztere diesen Anspruch überhaupt hat oder nicht.) |
Doch, sie leistet deutlich mehr, und zwar aus einem ganz einfachen Grund:
Wir haben es in der realen Welt mit einzelnen Quantensystemen zu tun, die wir einzeln präparieren, messen und beschreiben. Niemand zwingt uns, ein Ensemble zu betrachten. Deshalb ist eine Aussage über die „Realität“ eines einzelnen Quantensystems mehr wert, als eine Aussage über „gedachte“ Ensembles, die ggf.- gar nicht real sind.
| index_razor hat Folgendes geschrieben: | | Zitat: | | 2) Der zweite Knackpunkt für die Everettschen I. ist, dass es tatsächlich noch unklar ist, ob sie das Auftreten von Wahrscheinlichkeiten schlüssig erklären kann (Wallace; habe ich oben so geschrieben). Zur Erinnerung: es ist beweisbar, dass WENN ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt werden soll, dass dies DANN der (verallgemeinerten) Bornschen Regel entsprechen muss (Gleason); es ist NICHT beweisbar, dass ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt werden MUSS. |
Ich sehe kein Problem in der Unmöglichkeit zu beweisen, daß man irgendwo ein Wahrscheinlichkeitsmaß einführen MUSS. Wäre es eins, wäre es wohl ohnehin unlösbar. Aber selbst wenn ich das Auftreten von Wahrscheinlichkeiten einfach hinnehme, … |
Ich denke, da hast du etwas missverstanden.
Alle Interpretationen außer der Everettschen leben mit der Einführung von Wahrscheinlichkeiten per Postulat / Axiom. Ausschließlich in der Everettschen I. existiert per Axiom keine Wsk., jedoch nehmen wir diese (bzw. statistische Häufigkeiten) in der Praxis wahr. Daher muss die Everettsche I. erklären, wie in ihrem absolut deterministischen Kontext (!) eine Wahrscheinlichkeit ins Spiel kommen kann. Aufgrund ihres Anspruchs, dass ihre Aussagen jeweils für ein einzelnes System Gültigkeit haben (nicht für Ensembles), muss sie dies auf Ebene des Einzelsystems leisten.
Die Situation ist die, dass für die entsprechenden Strukturen (Bornsche Regel etc.) Verträglichkeitsbeweise existieren (Gleason, Hartle), dass jedoch bisher umstritten bleibt, warum diese zur Anwendung kommen sollen.
Also nochmal das zentrale Problem in andere Formulierung: Warum resultieren aus einer deterministischen Theorie (Quantenmechanik gemäß Everett) Phänomene, in denen statistische Häufigkeiten eine Rolle spielen?
| index_razor hat Folgendes geschrieben: | | Ich beurteile die Interpretation aber nicht nach ihren philosophischen Ansprüchen, sondern danach wie sie ihnen gerecht wird. Zumindest versuche ich das. Kann natürlich passieren, daß ich der Everettschen Interpretation unrecht tue. Ich sehe aber keinerlei ontologischen, philosophischen, oder sonstigen Vorsprung vor der Ensembleinterpretation. Die technischen Probleme innerhalb der MWI interessieren mich natürlich erst, wenn ich überzeugt bin, daß sie die philosophischen Ansprüche erfüllt, die ich teile und nicht schlimmere Probleme erzeugt. |
Die Everettsche I. bietet eine Ontologie für Einzelsystem: sie beschreib mittels eines Hilbertraumzustandes, was in einem einzelnen Quantensystem real geschieht. Das ist ein klarer Vorteil gegenüber rein statistischen Interpretationen (die Newtonsche Mechanik bietet im Kontext der klassischen Mechanik auch eine bessere Ontologie als die statistische Physik).
| index_razor hat Folgendes geschrieben: | | Zitat: | | Die Everettsche I. GLAUBT im Sinne einer philosophischen Überzeugung, dass dies so IST: Der Quantenzustand ist strukturell isomorph zu einer realen Katze, d.h. letztere IST REAL in einer derartigen Superposition. |
Das ist genau das, was ich als philosophischen Taschenspielertrick sehe. |
Das ist kein philosophischer Taschenspielertrick, sondern der philosophische Anspruch. Wenn du ihn nicht teilst, d.h. wenn du von der Physik nicht verlangst, dass sie die Realität isomorph abbildet, sondern wenn du damit zufrieden bist, dass sie Wahrscheinlichkeiten für Ergebnisse von Messungen voraussagt, dann hast du einen geringeren philosophischen Anspruch an die Physik.
| index_razor hat Folgendes geschrieben: | | Verstehe ich nicht. Wieso muß ich das Auftreten von Wahrscheinlichkeiten genau dann erklären, wenn ich irgendwelche ontologischen Ansprüche habe? |
Wenn du eine ontologische und streng deterministische Axiomatik und Interpretation einer physikalischen Theorie hast, (das ist die QM gem. der Everettschen I.), dann musst du das Auftreten von Waghrscheinlichkeiten oder statistischen Häufigkeiten erklären, da du diese in der Realität beobachtest. Das ist übrigens unter allen Befürwortzern und Kritikern der Everettschen I. unumstritten.
| index_razor hat Folgendes geschrieben: | | Warum Wahrscheinlichkeiten auftreten, ist allerdings auch einfach nicht die Frage um die es geht. |
Doch, natürlich. Wenn du sie nicht per Axiom einführst, musst du sie anderweitig begründen können.
| index_razor hat Folgendes geschrieben: | | Das Problem ist wie man den Meßprozeß realistisch erklären kann. |
Genau.
| index_razor hat Folgendes geschrieben: | | Die Ensembleinterpretation erklärt den Meßprozeß ganz einfach mit Hilfe von Wahrscheinlichkeiten: ~|zerfall>|tot> + |intakt>|lebendig> bedeutet: "Mit 50 % Wahrscheinlichkeit ist das Isotop zerfallen und die Katze tot, mit 50 % Wahrscheinlichkeit ist das Isotop nicht zerfallen und die Katze lebt noch. Andere Möglichkeiten gibt es nicht." Die Aussage stimmt zwar, und beschreibt eine simple Korrelation von Ereignissen, nur hat sie für eine vollständige Beschreibung des Vorgangs einen etwas dürftigen Bezug zur Realität der tatsächlich beobachteten Phänomene. |
Um es kurz zu machen, die Ensembleinterpretation beschreibt den Messprozess gerade nicht realistisch. Sie beschreibt den Input nicht realistisch, da sie lediglich mit Ensembles operiert, auch wenn in der Praxis nur ein einzelnes Quantensystem vorliegt, und sie beschreibt den Output nicht realistisch, da sie die unitäre Zeitentwicklung des Quantenzustandes nicht als real akzeptiert, sondenr lediglich als Werkzeug zur Berechnung von Wahrscheinlichkeiten.
Sie macht (wie viele andere Interpretationen) rein epistemische Aussagen.
| index_razor hat Folgendes geschrieben: | | Apodiktische Glaubensbekenntnisse wie "Der Zustand ist strukturell isomorph zum System." nehmen dieses Problem nicht mal ernst, fürchte ich. |
Dann wirst du die Everettsche I. nie wirklich verstehen, denn das ist ihre philosophische Grundeinstellung. Du musst diese Einstellung nicht teilen, aber du musst sie zumindest ernst nehmen, um die Everettsche I. diskutieren zu können (und ich meine, so blödsinnig ist die Idee nun auch wieder nicht; ansonsten wären Platon, Einstein, Penrose, … als Platonisten im Allgemeinen und Kenner sowie teilweise Unterstützer der Everettschen Interpretation wie Wheeler, deWitt, Deutsch, Carroll, … auch nicht ernst zu nehmen).
| index_razor hat Folgendes geschrieben: | | Einfach den Begriff des "Systems" so zu erweitern, daß er deckungsgleich mit der im Zustand verpackten Information ist, aber dabei das Problem zu ignorieren, wie sich aus diesem Zustand konkrete Phänomene ergeben, ist pure Rhetorik und schlechte Philosophie. |
Sorry, aber das geht völlig am Thema vorbei.
Das System wird nicht erweitert, sondern es entspricht exakt dem Systembegriff der QM, nämlich einem Zustandsvektor im Hilbertraum.
Außerdem wird das Problem, wie sich daraus konkrete Phänomene ergeben keineswegs ignoriert. Zum einen liefert die Dekohärenz ganz klar eine „effektiv klassische Welt“, oder in der Everettschen I. eine „Superposition effektiv klassischer, wechselweise unsichtbarer Welten“. Zum zweiten arbeitetn die Befürworter der Everettschen I. ja genau daran, das Auftreten von Wahrscheinlichkeiten bzw. Häufigkeiten zu erklären. Es sind alsdo gerade die Befürworter andere Interpretationen, die dieses Problem beiseite schieben (im Sinne von „shut up and calculate“) oder zusätzliche Postulate einführen („Kollaps-Postulat“).
Ich denke, du kritisierst in der Everettschen Interpretation Dinge, die sie schlichtweg nicht behauptet.
| index_razor hat Folgendes geschrieben: | | Die Ensembleinterpretation kann denselben Trick vollführen: System = Ensemble. Fertig. Damit ist offenbar eine 1-zu-1-Zuordnung von System und Zustand hergestellt, denn der Zustand beschreibt ein Ensemble. |
Das kann sie nur dann tun, wenn real ein Ensemble vorliegt. Sobald das nicht der Fall ist, hat die Ensemble-I. keinen realistischen, ontologischen Ansatzpunkt.
| index_razor hat Folgendes geschrieben: | | Wie sich aus dem Zustand nun konkrete Meßergebnisse ergeben, weiß man aber immer noch nicht. Genauso ist es bei Everett. Der Zustand beschreibt halt alle Zweige, schön und gut. Wieso scheinen nun die Phänomene genau einen Pfad durch diese Zweige auszuzeichnen? (Zur möglichen Antwort "Dekohärenz" komme ich weiter unten noch.) |
Nun, das liefert dir genau die Dekohärenz.
| index_razor hat Folgendes geschrieben: | | Ich habe noch mehr Ansprüche. Ich will nicht nur irgendeine Ontologie herbeidefiniert bekommen, sondern eine mit der man das Meßproblem realistisch erklären kann. Und genau das leistet die MWI m.E. nicht. Ansonsten erkläre mir, wieso "System = Ensemble" das Problem nicht genauso löst. |
Weil in der Praxis eben kein Ensemble vorliegen muss.
| index_razor hat Folgendes geschrieben: | | Es gibt keine klassischen Katzen. Es gibt nur Katzenensembles. |
Wenn ich genau eine Katze in meinem Garten sehe, dann sehe ich genau eine klassische Katze, kein Ensemble.
| index_razor hat Folgendes geschrieben: | | Warum ist System = Ensemble keine Ontologie, System = Menge aller Zweige aber schon? |
Weil in der Praxis eben kein Ensemble vorliegen muss.
| index_razor hat Folgendes geschrieben: | | Die Heranziehung von Dekohärenz als Grundlage für die Zweigstruktur erscheint mir im Hinblick auf die philosophischen Ansprüche, die du formulierst völlig unzureichend. Denn sie existiert ja nicht in isolierten Systemen, Everetts Viele Welten aber ja angeblich schon. |
Ich weiß nicht, auf welche Quellen du dich da beziehst.
Die heutige Auffassung der Everettschen I. besagt, dass die „Zweige“ letztlich den durch „einselection“ wechselweise unsichtbaren Komponenten des Zustandsvektors entsprechen. Über nichts anderes rede ich.
| index_razor hat Folgendes geschrieben: | | Wenn ich eine statistisch unbestimmte Wechselwirkung mit der Umgebung bräuchte, damit Zweige überhaupt entstehen, existierten keine Zweige im Universum, denn dieses hat keine Umgebung, mit der es wechselwirken kann. Die Zweige wären dann also kein fundamentales Konzept, sondern ein thermodynamisches. |
Ich denke, ich weiß, worauf du hinauswillst, auch wenn die Wortwahl ungeschickt ist.
Ja, die Zweige resultieren aus Beobachtersicht letztlich daraus, dass er die Umgebungsfreiheitsgrade nicht sämtlich beobachten kann. Dies führt zu einem „Ausspuren der Umgebungsfreiheitsgrade“ und zum Auftreten der Zweige. Wäre ein Beobachter in der Lage, alle Freiheitsgrade zu beobachten, würde er keine klassische Welt beobachten, sondern immer den vollen quantenmechanischen Zustand inklusive aller Superpositionen und Verschränkungen.
| index_razor hat Folgendes geschrieben: | | Zitat: | | Korrektur: die Everett-I. postuliert diese Zweige nicht, sie akzeptiert ihre Realität als Folgerung des Formalismus. Das ist mathematisch kein Unterschied, jedoch philosophisch bzw. axiomatisch ein ganz erheblicher. Die Everett-I. ist logisch konsistent, axiomatisch sparsam (im Sinne von Ockham). |
Was keine Folgerung ist, sollte man ehrlicherweise auch nicht als Folgerung bezeichnen. Postulat erscheint mir hier weitaus angemessener. Wenn die Realität der Zweige eine Folgerung aus dem Formalismus wäre, dann stünden alle Interpretation mit Ausnahme höchstens der Everettschen im Widerspruch zum Formalismus. Das tun sie natürlich nicht, sonst hätten wir hier nicht viel zu diskutieren. Also ist ihre Realität keine Folgerung, sondern einfach ein ontologisches Postulat. (Und mathematisch ist es natürlich schon ein Unterschied, ob ich eine Behauptung aus meinen Annahmen folgern kann oder sie postulieren muß.) |
Sorry, aber du argumentierst unsauber.
Ich sage nicht, dass die Realität der Zweige aus dem Formalismus folgt. Ich sage lediglich, dass die Zweige aus dem Formalismus folgen (und das tut sie unzweifelhaft im mathematischen Sinn), und dass ich ihre Existenz als real akzeptiere (d.h. kein zusätzliches Axiom oder Postulat einführe, um sie wegzudiskutieren).
Ich versuche, zwischen mathematischen Axiomen im Kontext des Formalismus sowie weiteren Postulaten, Annahmen oder Grundhaltung auf Ebene der Interpretation (Philosophie) zu unterscheiden.
| index_razor hat Folgendes geschrieben: | | Zweitens sehe ich im Augenblick auch ein logisches Problem, den Zweigen einen Produktzustand |a, relativ zu B>|B> zuzuordnen, der aus einem definitiven Beobachterzustand |B> und dem dazu relativen Systemzustand besteht, welches mir nicht lösbar erscheint … |
Klingt nach einem spannenden Argument, ich versteh’s aber nicht.
| index_razor hat Folgendes geschrieben: | | Ich habe gerade eben noch gelernt, daß eine Verallgemeinerung dieses Arguments offenbar als "Basisproblem" bekannt ist. Die einzig bekannte Lösung scheint Dekohärenz zu sein. Die greift allerdings nicht, wenn es um die fundamentale Frage der Realität der Zweige geht. Sie liefert nur die "Zweighaftigkeit" von Systemen im thermodynamischen Grenzwert. Das ist m.E. zu wenig. |
Ja, das ist aber auch nicht der Anspruch der Dekohärenz.
Zunächst löst die Dekohärenz nach gängiger Meinung (es gibt aber m.W.n. vereinzelte Gegenstimmen) das Problem der „preferred basis“. Dann sie löst das Problem, warum klassische bzw. „zweighafte“ Systeme resultieren. Darin eingeschlossen ist die wechselweise Unbeobachtbarkeit dieser Zweige (ich denke wieder, dass „thermodynamischer Grenzwert“ nicht der treffende Ausdruck ist; es geht um das Ausspuren praktisch unbeobachtbarer Umgebungsfreiheitsgrade).
Die Dekohärenz löst das Problem der Realität dieser Zweige tatsächlich nicht. Das ist auch nicht möglich, da die Dekohärenz schlichtweg eine mathematische Folgerung des Formalismus darstellt, nicht dessen Interpretation. Zusätzlich zur Dekohärenz kommen nun Interpretationen ins Spiel. Manche davon besagen, dass nur ein Zweig real existent bleibt. Andere besagen, dass wir ab der Messung nur noch den Zweig für weitere Berechnungen verwenden sollen, der dem gemessen Ergebnis entspricht. Die Everettsche I. besagt, dass alle Zweige real existent bleiben.
Die Dekohärenz ist jedoch ein starkes Indiz dafür, dass die Everettsche I. sinnvoll ist, da sie sozusagen zur Hälfte die Arbeit bereits erledigt hat. Auf Basis der Dekohärenz scheint die Everettsche I. jedenfalls natürlicher zu sein als ohne sie (ich denke, dass gertade die Dekohärenz dazu beigetragen hat, dass diese I. überhaupt wieder salonfähig wurde).
Anbei ein paar interessante Links
http://plato.stanford.edu/entries/qm-manyworlds/
http://www.preposterousuniverse.com/blog/2015/02/19/the-wrong-objections-to-the-many-worlds-interpretation-of-quantum-mechanics/ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 01. Sep 2015 08:20 Titel: TomS Verfasst am: 01. Sep 2015 08:20 Titel: |
 |
|
Vielleicht sollten wir nochmal ganz von vorne starten, um die Intention der Everettschen Interpretation (für sich alleine und ohne Bezug zu anderen Interpretationen) klarzustellen (da wir Interpretationen nicht vergleichen oder werten sollten, bevor sie klar definiert sind).
Gegeben sei ein Produkthilbertraum "Quantensystem * Messgerät * Umgebung" sowie die unitäre Zeitentwicklung im Kontext einer "Messung (= Interaktion des Quantensystems mit dem Messgerät sowie mit der Umgebung) gem. Schrödungergleichung:
\,|0\rangle\,|E\rangle \;\to\; (|a\rangle\,|A\rangle + |b\rangle\,|B\rangle)\,|E^\prime\rangle + \ldots)
Die Dekohärenz besagt, dass aus dieser Interaktion eine Zweigstruktur dergestalt resultiert, dass die mikroskopische Superposition |a> + |b> im Eingangszustand zu einer makroskopischen Superposition |aA...> + |bB...> + ... im Endzustand führt. Jede Komponente |aA...>, ... des Gesamtzustandes repräsentiert einen "Zweig". Diese Zweige sind jeweils stabil und wechselweise unsichtbar. Die Dekohärenz erklärt demnach, wie und warum makroskopische "Zeigerzustände" |aA>, ... resultieren und warum wir nur diese wahrnehmen, d.h. warum erstens die Superposition an sich unsichtbar ist und (beoachter-lokal) nur ein Zweig sichtbar ist, und warum zweitens nicht-diagonale Komponenten der Form |aB> dynamisch unterdrückt und damit unsichtbar sind.
Die Everett-Interpretation besagt nun, dass beide Zustände (= vor sowie nach der Messung) bzgl. eines einzelnen Quantensystems sowie eines Messgeräts mit UMgebung als real in dem Sinne gelten, dass beide Zustände jeweils strukturell isomorph zum tatsächlich existierenden, physikalischen Gesamtsystem sind.
D.h. zum einen reduziert die E.-I. den Quantenzustand nicht auf ein mathematisches Konstrukt, das lediglich eine gewisse Information trägt bzw. zur Berechnung von beobachtbaren Phänomenen dient, sondern der beschreibt, was tatsächlich real in der Natur existiert. Zum anderen besagt die E.-I., dass dies tatsächlich für jeweils ein einzelnes Quantensystem gilt. Und zuletzt akzeptiert die E.-I., dass die im Zuge der Dekohärenz resultierende Zweigstruktur als "Superposition wechselweise unsichtbarer klassischer Zweige" tatsächlich im o.g. Sinn real existent bleibt, d.h. dass rechts diese Zweigstruktur wiederum beschreibt, was tatsächlich real in der Natur existiert.
Während andere Interpretationen also einen Quantenzustand dergestalt interpretieren, dass er Berechnungen von Phänomenen und deren Wahrscheinlichkeiten erlaubt, interpretieren Everett et al. den Quantenzustand als mathematisch isomorphe Repräsentation des tatsächlichen realen Prozesses bzw. Vorgangs in der Natur. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 01. Sep 2015 10:34 Titel: bassiks Verfasst am: 01. Sep 2015 10:34 Titel: |
 |
|
Das ist eine sehr interessante Diskussion. Aus zeitlichen Gründen habe ich sie allerdings nur etwas überflogen. Falls ich jetzt etwas schreibe was bereits diskutiert wurde, ignoriert mich bitte einfach.
Zum Thema Ensemble-Interpretation: Der Schwachpunkt der Ensemble Interpretation ist meiner Meinung nach nicht rein philosophisch. Wenn man behauptet der Zustand beschreibt lediglich ein Ensemble etc., dann stellt sich die Frage ob der Zustand alles ist was wir über das System wissen können. Das wirft für mich fast zwangsläufig die Forderung nach verborgenen Parametern auf. Das ist prinzipiell noch kein kritisches Problem (meines Wissens nach sind nicht alle verborgenen Parameter-Modelle verboten), aber aus heutiger sicht auch nicht unbedingt befriedigend.
Die E. I. hat dieses Problem nicht. Bei der E. I. bleibt für mich derzeit noch die Frage nach den Wahrscheinlichkeiten ungeklärt. Ich denke ich habe noch nicht 100% verstanden wie die E.I den letzten Schritt der Messung erklären kann.
| Zitat: | | "Suoerposition wechselweise unsichtbarer klassischer Welten" |
Ich würde in diesem Zitat klassische Welten durch quasiklassische Welten erklären. Die Dekohärenz sorgt für die Zweighaftigkeit und die einzelne Messung verschiebt sich damit für mich auf die Frage, wie wird entschieden in welchem dieser Zweige ich bin. Kurz gesagt fehlt mir momentan einfach noch der finale Baustein, warum die E.I das Messproblem lösen sollte. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 01. Sep 2015 12:59 Titel: TomS Verfasst am: 01. Sep 2015 12:59 Titel: |
 |
|
| bassiks hat Folgendes geschrieben: | | Zum Thema Ensemble-Interpretation: Der Schwachpunkt der Ensemble Interpretation ist meiner Meinung nach nicht rein philosophisch. Wenn man behauptet der Zustand beschreibt lediglich ein Ensemble etc., dann stellt sich die Frage ob der Zustand alles ist was wir über das System wissen können. |
Das ist richtig, das ist genau der wesentliche Kritikpunkt an der Ensemble-I.:
| D. Mermin hat Folgendes geschrieben: | | The second motivation for an ensemble interpretation is the intuition that because quantum mechanics is inherently probabilistic, it only needs to make sense as a theory of ensembles. Whether or not probabilities can be given a sensible meaning for individual systems, this motivation is not compelling. For a theory ought to be able to describe as well as predict the behavior of the world. The fact that physics cannot make deterministic predictions about individual systems does not excuse us from pursuing the goal of being able to describe them as they currently are. |
| A. Neumaier hat Folgendes geschrieben: | | Among the traditional interpretations, the statistical interpretation discussed by Ballentine in Rev. Mod. Phys. 42, 358-381 (1970) is the least demanding (assumes less than the Copenhagen interpretation and the Many Worlds interpretation) and the most consistent one. It explains almost everything, and only has the disadvantage that it explicitly excludes the applicability of QM to single systems or very small ensembles ... |
Ich behaupte aber, dass das schon im wesentlichen eine philosophische Kritik ist.
Wenn ich den positivistischen Standpunkt einnehme, dass jegliche Ontologie jenseits von messbaren Phänomene irrelevant ist, dann bin ich (u.a.) mit der Ensemble-I. gut bedient. Sie erlaubt es, Messergebnisse (Eigenwerte) und deren Wahrscheinlichkeiten zu berechnen. Da die Arbeitsweise der Physiker dergestalt ist, dass sie Experimente durchführen und wiederholen, entspricht die Ensemble-I. direkt der experimentellen Praxis; kein Physiker wird ein Paper veröffentlichen, in dem er genau ein einzelnes Quantenobjekt genau einmal untersucht hat.
Wenn ich diesen positivistischen (phänomenologischen) Standpunkt jedoch nicht vertrete, sondern der Meinung bin, dass der mathematische Formalismus (im platonistischen Sinn) einer mehr oder weniger isomorphe Abbildung der unabhängig existierenden Realität ist, dann - und erst dann - macht die Everettsche Interpretation überhaupt erst Sinn. Und auch erst dann muss ich zwangsläufig ein Kollapspostulat ablehnen, da nicht sowohl die unitäre Zeitentwicklung als auch der Kollaps gleichermaßen real sein können, da nicht eine Wechselwirkung einmal als das eine und einmal als das andere sein kann; dies wäre widersprüchlich. Und auch erst dann muss ich eine statistische Interpretation ablehnen, denn diese muss sich zwangsläufig immer auf ein Ensemble beziehen, das aber im konkreten Fall gar nicht vorzuliegen braucht. Natürlich kann ich auch in einer anderen Interpretation von diversen Theoremen (Gleason, Hartle) Gebrauch machen, zwingend mit dem Problem der Wahrscheinlichkeit auseinandersetzen muss ich mich jedoch nur inder Everettschen Interpretation, da diese gemäß ihrer Axiome streng deterministisch ist (sein muss), und daher anderweitig erklären muss, wie und warum Beobachter- bzw. Zweig-lokal Wahrscheinkllichkeiten wahrgenommen werden.
| bassiks hat Folgendes geschrieben: | | Das wirft für mich fast zwangsläufig die Forderung nach verborgenen Parametern auf. Das ist prinzipiell noch kein kritisches Problem (meines Wissens nach sind nicht alle verborgenen Parameter-Modelle verboten), aber aus heutiger sicht auch nicht unbedingt befriedigend. |
Verborgene Variablen o.ä. benötige ich erst dann, wenn ich über etwas sprechen will, das real existiert, ohne dass ich es wahrnehme, z.B. wenn ich einem Quantenzustand eine unbeobachtbare, jedoch reale Eigenschaft zusprechen möchte. Wenn ich den Quantenzustand nicht ontologisch interpretiere, besteht dafür keine Veranlassung.
| bassiks hat Folgendes geschrieben: | | Bei der E. I. bleibt für mich derzeit noch die Frage nach den Wahrscheinlichkeiten ungeklärt. Ich denke ich habe noch nicht 100% verstanden wie die E.I den letzten Schritt der Messung erklären kann. |
Das habe ich auch noch nicht erklärt.
Betrachten wir einen Superpositionszustand der Form
\,|0\rangle\,|E\rangle \;\to\; (c_a|a\rangle\,|A\rangle + c_a|b\rangle\,|B\rangle)\,|E^\prime\rangle + \ldots)
Ich weiß sicher, dass ich den ersten Zustand genau so präpariere. Ich behaupte, dass durch die Messung der zweite Zustand entsteht und beide Zweige real existent sind. In einem geeigneten, größeren Produkthilbertraum bin ich selbst als Beobachter von dieser Verzweigung betroffen, d.h. ich kann |aA> interpretieren als "Beobachter beobachtet Messgerät, das "a" registriert" und "A" anzeigt" (|bB> analog).
Wenn dies tatsächlich "meine" Zweig-lokale Realität ist, dann muss ich erklären können, wieso die Vorfaktoren der Zweige bei wiederholter Durchführung derartiger Messungen in statistischen Häufigkeiten resultieren.
Man beachte: eine naive Abzählung der Zweige funktioniert nicht!! Diese ergäbe immer 2 Zweige, d.h. Wahrscheinlichkeiten 1/2. Die Experimente ergeben jedoch
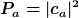
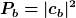
in Übereinstrimmung mit der Bornschen Regel, die ich jedoch nicht als Axiom einführen will (denn die Theorie ist ja streng deterministisch). Wenn die Theorie jedoch streng deterministisch ist, und ich daher keine Wahrscheinlichkeit einführen kann und darf, dann bleibt die wesentliche Herausforderung, woher denn überhaupt Wahrtscheinlichkeiten resultieren können (die ich ja zweifelsohne kosnsistent anwenden kann).
Der Ausweg wie in der statistischen Mechanik ist auch nicht möglich, denn dort resultieren Wahrscheinlichkeiten aus unvollständigem Wissen. Dies ist hier jedoch nicht der Fall, denn die o.g. Zustände sind exakt bekannt und kodieren das System deterministisch und vollständig; es gibt kein unvollständiges Wissen in der Everettschen I., und es gibt keine unvollständige Repräsentation des "realen" Zustandes (im Sinne von verborgenen Variablen o.ä.).
Das - und m.E. nur das - ist die wesentliche Herausforderung an die Everettsche I.
| bassiks hat Folgendes geschrieben: | | Zitat: | | "Superposition wechselweise unsichtbarer klassischer Welten" |
Ich würde in diesem Zitat klassische Welten durch quasiklassische Welten erklären. Die Dekohärenz sorgt für die Zweighaftigkeit und die einzelne Messung verschiebt sich damit für mich auf die Frage, wie wird entschieden in welchem dieser Zweige ich bin. Kurz gesagt fehlt mir momentan einfach noch der finale Baustein, warum die E.I das Messproblem lösen sollte. |
Die Frage ist nicht, wie und warum ich in einem Zweig bin; auch das "Ich" verzweigt sich als Bestandteil des Gesamtsystems entsprechend der o.g. Zweigstruktur., d.h. mein "Ich" wird "zweighaft". Die Frage ist, warum es konsistent ist, anzunehmen, dass die Vorfaktoren der Zweige zu relativen Häufigkeiten führen.
Die Everettsche I. löst das Messproblem unter genau der Annahme, dass sie dieses Problem der "emergenten Wahrscheinlichkeit" lösen kann.
Zunächst mal besteht das Messproblem aus mehrere Ebenen, die ich wie folgt skizzieren würde:
1) Messung im Gegensatz zu normaler Wechselwirkung
2) dynamische Selektion einer bestimmten Basis
3) Erscheinen wechselweise unsichtbarer quasiklassischer Zweige in dieser Basis
4) Anwendbarkeit von Wahrscheinlichkeiten auf Messreihen trotz einer fundamental deterministischen Theorie
1) wird trivialerweise gelöst durch die Axiomatik der Everettschen I. Es gibt schlichtweg nichts in den Axiomen oder dem Formalismus, was eine Messung von einer gewöhnlichen Wechselwirkung unterscheidet.
2) wird gelöst von der Dekohärenz; wenn ich die Observable A messe, dann verzweigt sich das System entsprechend der Eigenzustände von A (man betrachte z.B. ein Spin-Singulett; dieses kann ich bzgl. jeder beliebigen Achse definieren, aber die Festlegung, dass ich die z-Komponente messe, führt zu einer Verzweigung entsprechend der z-Komponente, nicht bzgl. ein er anderen wie z.B. der x-Komponente)
3) wird ebenfalls gelöst von der Dekohärenz
4) muss gelöst werden mittels weiterer Argumente (und ggf. zusätzlicher Annahmen), aus denen das Auftreten von Wahrscheinlichkeiten in natürlicher Weise folgt; dazu gibt es eine Reihe unterschiedlicher Ansätze; ich denke, man ist sich heute weitgehend einig, dass keiner wirklich allgemein akzeptiert und "natürlich" ist.
Sucht mal nach "Born Rule" sowie den Autoren "Wallace", Sounders", "Carroll" "Zurek".
Eine lesenswerte Zusammenfassung sowie weitere Links gibt's hier:
http://www.preposterousuniverse.com/blog/2014/07/24/why-probability-in-quantum-mechanics-is-given-by-the-wave-function-squared/
| Carroll hat Folgendes geschrieben: | | Note that the pressing question is not so much “Why is the probability given by the wave function squared ... as it is “Why is there a particular probability rule at all, since the theory is deterministic?” Indeed, once you accept that there should be some specific probability rule, it’s practically guaranteed to be the Born Rule. There is a result called Gleason’s Theorem, which says roughly that the Born Rule is the only consistent probability rule you can conceivably have that depends on the wave function alone. So the real question is not “Why squared?”, it’s “Whence probability?” |
| Zurek hat Folgendes geschrieben: | | Indeed, Gleason’s theorem is now an accepted and rightly famous part of quantum foundations. It is rigorous – it is after all a theorem about measures on Hilbert spaces. However, regarded as a result in physics it is deeply unsatisfying: it provides no insight into physical significance of quantum probabilities – it is not clear why the observer should assign probabilities in accord with the measure indicated by Gleason’s approach. |
Ich denke, das bringt es sehr gut auf den Punkt. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 01. Sep 2015 13:45 Titel: bassiks Verfasst am: 01. Sep 2015 13:45 Titel: |
 |
|
| Zitat: | | Die Frage ist, warum es konsistent ist, anzunehmen, dass die Vorfaktoren der Zweige zu relativen Häufigkeiten führen. |
Das ist das was ich mit dem "wie wird entschieden" meinte. Wir hatten ja bereits öfter darüber geredet und ich denke wir sind im wesentlichen der selben Meinung (inklusive der Feststellung dass "Many worlds" irgendwie eine nicht so günstige Bezeichnung ist, weshalb ich E.I bevorzuge), was die E.I angeht.
EDIT: Danke für den Link! Sehr interessant! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Sep 2015 20:15 Titel: index_razor Verfasst am: 01. Sep 2015 20:15 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
| Zitat: | | Zitat: |
Es ist wichtig, diesen philosophischen Anspruch zu verstehen. |
Ich verstehe diesen philosophischen Anspruch durchaus und teile ihn auch. Ich meine aber, daß die MWI, trotz des größeren Anspruchs, in dieser Hinsicht genauso wenig leistet, wie die Ensembleinterpretation. (Egal, ob letztere diesen Anspruch überhaupt hat oder nicht.) |
Doch, sie leistet deutlich mehr, und zwar aus einem ganz einfachen Grund:
Wir haben es in der realen Welt mit einzelnen Quantensystemen zu tun, die wir einzeln präparieren, messen und beschreiben. Niemand zwingt uns, ein Ensemble zu betrachten. Deshalb ist eine Aussage über die „Realität“ eines einzelnen Quantensystems mehr wert, als eine Aussage über „gedachte“ Ensembles, die ggf.- gar nicht real sind.
|
Du argumentierst zirkulär. Die Frage womit wir es in der realen Welt zu tun haben, ist genau jene, die die Interpretation (bzw. deren Ontologie) beantworten soll. Also kannst du als Argument gegen eine Interpretation nicht anführen, was deiner vorgefaßten Meinung nach real existiert. Mein hypothetischer "Ensemble-Ontologe" kann genauso behaupten, es existieren nicht viele reale Welten, sondern nur eine, aber diese sei ein Ensemble. In seiner Sichtweise zwingt uns natürlich genau die Tatsache, daß der Zustand eine Wahrscheinlichkeitsamplitude beschreibt, die reale Existenz von Ensembles anzunehmen. Du bezeichnest die Ensembles als "gedacht", aber nur wegen deiner ontologischen Vorurteile. Du denkst auch nur, daß du ein einzelnes System präparierst, stattdessen ensteht immer ein Ensemble (Teilensemble eines großen Universumsensembles).
Um es sicherheitshalber gleich dazu zu sagen: diese Interpretation wird zurecht von niemandem ernst genommen und ich vertrete sie nicht. Aber vollführt man stattdessen in der Begriffswelt der MWI genau dieselbe sophistische Augenwischerei, wird es plötzlich für hohe Philosophie gehalten. Mein Einwand zielt gerade darauf, daß die Zweige genauso eine Fiktion sind wie die Ensembles (bzw. deren Mitglieder).
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zitat: | | 2) Der zweite Knackpunkt für die Everettschen I. ist, dass es tatsächlich noch unklar ist, ob sie das Auftreten von Wahrscheinlichkeiten schlüssig erklären kann (Wallace; habe ich oben so geschrieben). Zur Erinnerung: es ist beweisbar, dass WENN ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt werden soll, dass dies DANN der (verallgemeinerten) Bornschen Regel entsprechen muss (Gleason); es ist NICHT beweisbar, dass ein Wahrscheinlichkeitsmaß auf einem Hilbertraum eingeführt werden MUSS. |
Ich sehe kein Problem in der Unmöglichkeit zu beweisen, daß man irgendwo ein Wahrscheinlichkeitsmaß einführen MUSS. Wäre es eins, wäre es wohl ohnehin unlösbar. Aber selbst wenn ich das Auftreten von Wahrscheinlichkeiten einfach hinnehme, … |
Ich denke, da hast du etwas missverstanden.
|
Ich wollte dir nur mitteilen, daß ich die Probleme an anderer Stelle sehe. Egal ob ich die Wahrscheinlichkeiten postuliere oder ableite -- wenn ich sie erstmal in den Grundstrukturen (Zustand) der Theorie habe, entsteht sofort das Problem zu interpretieren, was beim Meßvorgang real passiert. Daran änderte sich überhaupt nichts, wenn bewiesen wäre, daß ich Wahrscheinlichkeiten unbedingt einführen muß.
| Zitat: |
Alle Interpretationen außer der Everettschen leben mit der Einführung von Wahrscheinlichkeiten per Postulat / Axiom.
|
Selbst wenn es stimmte, es ist vollkommen unerheblich. Die Frage ob ich die Wahrscheinlichkeiten in der Theorie postulieren muß oder ableiten kann, ist eine rein logische und hat mit der Interpretation nicht das geringste zu tun. Ich kann einfach alle logischen Beziehungen zwischen allen wahren Aussagen der QM ignorieren, sie alle wie Postulate behandeln und habe exakt gar nichts am Interpretationsproblem geändert. Es existiert genau wie vorher.
| Zitat: |
Ausschließlich in der Everettschen I. existiert per Axiom keine Wsk., jedoch nehmen wir diese (bzw. statistische Häufigkeiten) in der Praxis wahr. Daher muss die Everettsche I. erklären, wie in ihrem absolut deterministischen Kontext (!) eine Wahrscheinlichkeit ins Spiel kommen kann. Aufgrund ihres Anspruchs, dass ihre Aussagen jeweils für ein einzelnes System Gültigkeit haben (nicht für Ensembles), muss sie dies auf Ebene des Einzelsystems leisten.
|
Da ich das Thema als unwichtig bezeichnet habe, sollte ich es vielleicht auf sich beruhen lassen. Mich interessiert aber trotzdem was du denkst, was Everett im Abschnitt "Observation" in seinem Rev.Mod.Phys.-Artikel macht. Er stellt dort axiomatisch die Eigenschaften zusammen, die er für eine Miniatur-Maßtheorie benötigt und dann leitet er ab, daß diese Eigenschaften nur vom Betragsquadrat der Wellenfunktion erfüllt werden können. Er nennt es eben nur nicht "Wahrscheinlichkeit", sondern "Maß" bzw. "Gewicht". Und was ist die Motivation für dieses Maß?
"In order to establish quantitative results, we must put some sort of measure (weighting) on the elements of a final superposition.[...] We wish to make quantitative statements about the relative frequencies of the different possible results of observation---which are recorded in the memory---for a typical observer state;[...]" (Everett, 1957, meine Hervorhebung)
Was ist das anderes als ein Wahrscheinlichkeitsmaß? Nur weil es nicht ganz am Anfang steht, ist es nicht weniger axiomatisch.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ich beurteile die Interpretation aber nicht nach ihren philosophischen Ansprüchen, sondern danach wie sie ihnen gerecht wird. Zumindest versuche ich das. Kann natürlich passieren, daß ich der Everettschen Interpretation unrecht tue. Ich sehe aber keinerlei ontologischen, philosophischen, oder sonstigen Vorsprung vor der Ensembleinterpretation. Die technischen Probleme innerhalb der MWI interessieren mich natürlich erst, wenn ich überzeugt bin, daß sie die philosophischen Ansprüche erfüllt, die ich teile und nicht schlimmere Probleme erzeugt. |
Die Everettsche I. bietet eine Ontologie für Einzelsystem: sie beschreib mittels eines Hilbertraumzustandes, was in einem einzelnen Quantensystem real geschieht. Das ist ein klarer Vorteil gegenüber rein statistischen Interpretationen (die Newtonsche Mechanik bietet im Kontext der klassischen Mechanik auch eine bessere Ontologie als die statistische Physik).
|
Die Newtonsche Mechanik macht auch sehr spezifische Angaben über die Zustände, in denen sich die Systeme innerhalb eines klassischen statistischen Ensembles befinden können: Sie sind eindeutig durch Orte und Impulse aller Teilchen, also Punkte im Phasenraum, spezifiziert, während das ganze Ensemble durch eine Wahrscheinlichkeitsverteilung über diesem Phasenraum charakterisiert ist. Die MWI hat genau mit dieser eindeutigen Spezifikation Probleme. Sie behauptet zwar einfach ein Zustand beschreibe viele Welten, kann aber außerhalb gewisser Näherungen nicht eindeutig sagen, in welchem Zustand sich diese Welten befinden. Insofern sehe ich nicht, daß sie hier ontologisch allzuviel bietet, von einem klaren Vorteil ganz zu schweigen. (Das gilt für die Ensembleinterpretation natürlich auch.)
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zitat: | | Die Everettsche I. GLAUBT im Sinne einer philosophischen Überzeugung, dass dies so IST: Der Quantenzustand ist strukturell isomorph zu einer realen Katze, d.h. letztere IST REAL in einer derartigen Superposition. |
Das ist genau das, was ich als philosophischen Taschenspielertrick sehe. |
Das ist kein philosophischer Taschenspielertrick, sondern der philosophische Anspruch. Wenn du ihn nicht teilst, d.h. wenn du von der Physik nicht verlangst, dass sie die Realität isomorph abbildet, sondern wenn du damit zufrieden bist, dass sie Wahrscheinlichkeiten für Ergebnisse von Messungen voraussagt, dann hast du einen geringeren philosophischen Anspruch an die Physik.
|
Nochmal, ich gebe mich keineswegs mit Wahrscheinlichkeitsaussagen zufrieden. Daß ich gewisse Ansprüche mit den MWI-Anhängern teile, heißt aber nicht, daß ich mir von ihnen gern ein X für ein U vormachen lasse. Dein Satz über die Realität der Katze besagt doch nicht viel mehr, als "Was auch immer der Zustand eben beschreibt, das ist das reale System." Das hat nicht das geringste mit einer konkreten Interpretation zu tun. Derart rumtricksen kann man in jeder Interpretation.
Um es nochmal deutlich zu sagen: Uneinigkeit sehe ich nicht sowohl in den philosophischen Ansprüchen, wie in der Bewertung der vorgeschlagenen Lösung.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Warum Wahrscheinlichkeiten auftreten, ist allerdings auch einfach nicht die Frage um die es geht. |
Doch, natürlich. Wenn du sie nicht per Axiom einführst, musst du sie anderweitig begründen können.
|
Für die Frage, um die es ging, ist es egal, ob die Wahrscheinlichkeiten per Axiom einführe oder anderweitig begründe. Generell ist das Thema, ob eine Aussage der Theorie ein Axiom oder ein Theorem ist, von völlig untergeordneter Bedeutung. Eine Frage der Interpretation ist, was die Theorie, also die Gesamtheit ihrer Aussagen, bedeutet, nicht, welche ihrer Aussagen ich aus welchen ableiten kann.
| Zitat: | | index_razor hat Folgendes geschrieben: | | Die Ensembleinterpretation erklärt den Meßprozeß ganz einfach mit Hilfe von Wahrscheinlichkeiten: [...] |
Um es kurz zu machen, die Ensembleinterpretation beschreibt den Messprozess gerade nicht realistisch. Sie beschreibt den Input nicht realistisch, da sie lediglich mit Ensembles operiert, auch wenn in der Praxis nur ein einzelnes Quantensystem vorliegt, und sie beschreibt den Output nicht realistisch, da sie die unitäre Zeitentwicklung des Quantenzustandes nicht als real akzeptiert, sondenr lediglich als Werkzeug zur Berechnung von Wahrscheinlichkeiten.
Sie macht (wie viele andere Interpretationen) rein epistemische Aussagen.
|
Ich weiß, daß sie ihn nicht realistisch beschreibt. Das wollte ich ja gerade damit ausdrücken. Ich will ja die Ensembleinterpretation nicht als Lösung des Meßproblems vorschlagen, sondern sie nur gegen unfaire Vergleiche verteidigen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Apodiktische Glaubensbekenntnisse wie "Der Zustand ist strukturell isomorph zum System." nehmen dieses Problem nicht mal ernst, fürchte ich. |
Dann wirst du die Everettsche I. nie wirklich verstehen, denn das ist ihre philosophische Grundeinstellung. Du musst diese Einstellung nicht teilen, aber du musst sie zumindest ernst nehmen, um die Everettsche I. diskutieren zu können (und ich meine, so blödsinnig ist die Idee nun auch wieder nicht; ansonsten wären Platon, Einstein, Penrose, … als Platonisten im Allgemeinen und Kenner sowie teilweise Unterstützer der Everettschen Interpretation wie Wheeler, deWitt, Deutsch, Carroll, … auch nicht ernst zu nehmen).
|
Mißverständnis? Ich habe nicht gesagt, daß ich die MWI oder ihre Vetreter nicht ernst nehme. Ich behaupte nur, daß ihre Vertreter, zumindest sofern sie dieses Glaubensbekenntnis als Lösung des Meßproblems ansehen, das Meßproblem nicht besonders ernstnehmen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Einfach den Begriff des "Systems" so zu erweitern, daß er deckungsgleich mit der im Zustand verpackten Information ist, aber dabei das Problem zu ignorieren, wie sich aus diesem Zustand konkrete Phänomene ergeben, ist pure Rhetorik und schlechte Philosophie. |
Sorry, aber das geht völlig am Thema vorbei.
Das System wird nicht erweitert, sondern es entspricht exakt dem Systembegriff der QM, nämlich einem Zustandsvektor im Hilbertraum.
|
Langsam. Das "System" war das Ding was real existiert und seine Relation zum "Zustandsvektor im Hilbertraum", also dem was die QM über dieses Ding aussagt, ist genau das grundlegende Interpretationsproblem der Quantenmechanik. Wenn etwas am Thema vorbei geht, dann die unreflektierte Verwendung dieser beiden Begriffe als Synonyme. Aber es ist ja genau mein Vorwurf an dich, daß hinter der ganzen Ontologie der MWI, zumindest so wie du sie darstellst, nichts weiter steckt als diese nominelle Gleichsetzung: Es existiert genau das, was der Zustandsvektor eben beschreibt und das nennen wir "System". Daß dieses System aus realen Zweigen besteht, folgt bereits nicht mehr aus dem Formalismus und ist reine Fiktion.
| Zitat: |
Außerdem wird das Problem, wie sich daraus konkrete Phänomene ergeben keineswegs ignoriert. Zum einen liefert die Dekohärenz ganz klar eine „effektiv klassische Welt“, oder in der Everettschen I. eine „Superposition effektiv klassischer, wechselweise unsichtbarer Welten“. Zum zweiten arbeitetn die Befürworter der Everettschen I. ja genau daran, das Auftreten von Wahrscheinlichkeiten bzw. Häufigkeiten zu erklären. Es sind alsdo gerade die Befürworter andere Interpretationen, die dieses Problem beiseite schieben (im Sinne von „shut up and calculate“) oder zusätzliche Postulate einführen („Kollaps-Postulat“).
|
Ich meine mit Phänomen die Tatsache, daß bei jeder Einzelmessung genau ein Meßwert auftaucht. Dies ist erst dann ein Problem, wenn meine vollständige Beschreibung des Systems Wahrscheinlichkeiten enthält. Die fleißigen Bemühungen diese Wahrscheinlichkeiten abzuleiten, können dieses Problem nicht lösen, sondern nur zeigen, daß es notwendig auftritt.
Dekohärenz liefert mir nur in bestimmten Situationen eine plausible realistische Erklärung für dieses Phänomen. Nämlich sofern man sinnvoll behaupten kann: Der Meßwert a erscheint mit der Wahrscheinlichkeit p(a), da sich das System mit derselben Wahrscheinlichkeit in einem Zustand befindet, in dem a mit Sicherheit auftritt. Aber gerade dieser Fall funktioniert zumindest in der Ensembleinterpretation genauso gut. Die Fälle, in denen dies nicht geht sind deshalb die aus Sicht der Interpretation interessanten.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Die Ensembleinterpretation kann denselben Trick vollführen: System = Ensemble. Fertig. Damit ist offenbar eine 1-zu-1-Zuordnung von System und Zustand hergestellt, denn der Zustand beschreibt ein Ensemble. |
Das kann sie nur dann tun, wenn real ein Ensemble vorliegt. Sobald das nicht der Fall ist, hat die Ensemble-I. keinen realistischen, ontologischen Ansatzpunkt.
|
Ja natürlich. Woher weißt du, daß keins vorliegt?
Die MWI kann nur dann behaupten, daß die Katze eine Superposition IST, wenn beide Zweige real vorliegen. Ansonsten hat sie keinen realistischen, ontologischen Ansatzpunkt. Woher weißt du, daß beide Zweige existieren?
Das ist dieselbe zirkuläre Argumentation wie oben.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ich habe noch mehr Ansprüche. Ich will nicht nur irgendeine Ontologie herbeidefiniert bekommen, sondern eine mit der man das Meßproblem realistisch erklären kann. Und genau das leistet die MWI m.E. nicht. Ansonsten erkläre mir, wieso "System = Ensemble" das Problem nicht genauso löst. |
Weil in der Praxis eben kein Ensemble vorliegen muss.
|
Behauptest du. Mehrere Zweige liegen "in der Praxis" auch nicht vor, sondern nur immer einer.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Es gibt keine klassischen Katzen. Es gibt nur Katzenensembles. |
Wenn ich genau eine Katze in meinem Garten sehe, dann sehe ich genau eine klassische Katze, kein Ensemble.
|
Was du siehst und was existiert sind zwei völlig verschiedene Dinge. Du siehst ja auch nicht beide Zweige deiner Superpositionskatze. Aber vielleicht verstehst du ja jetzt besser, was ich mit der Diskrepanz zwischen Phänomenen und Zustandsbeschreibung gemeint habe, da du das Argument hier ja jetzt selbst verwendet hast. Aus genau diesem Grund halte ich "System = Ensemble" für nicht besonders befriedigend. System = Menge von Zweigen ist allerdings genauso wenig überzeugend, denn den Zweigen kann nicht unter allen Umständen reale Existenz zugesprochen werden. In den Fällen, in denen es geht, habe ich auch ein statistisches Ensemble.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Warum ist System = Ensemble keine Ontologie, System = Menge aller Zweige aber schon? |
Weil in der Praxis eben kein Ensemble vorliegen muss.
|
Das "in der Praxis" gefällt mir gut. Ich dachte wir sprechen über Ontologie. In welchem Sinne liegen "in der Praxis" mehrere Zweige vor?
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Die Heranziehung von Dekohärenz als Grundlage für die Zweigstruktur erscheint mir im Hinblick auf die philosophischen Ansprüche, die du formulierst völlig unzureichend. Denn sie existiert ja nicht in isolierten Systemen, Everetts Viele Welten aber ja angeblich schon. |
Ich weiß nicht, auf welche Quellen du dich da beziehst.
|
Everett, Rev.Mod.Phys. 29 (1957). Darin ist natürlich von Dekohärenz nicht die Rede. Er wendet die Viele-Welten-Interpretation ausdrücklich auf geschlossenen Systeme in reinen Zuständen an, nicht auf Gemische. Im übrigen kann man gerade Gemische mit "preferred basis" ohne Probleme realistisch als Ensembles interpretieren.
| Zitat: |
Die heutige Auffassung der Everettschen I. besagt, dass die „Zweige“ letztlich den durch „einselection“ wechselweise unsichtbaren Komponenten des Zustandsvektors entsprechen. Über nichts anderes rede ich.
|
Klar, wenn man die MWI einmal akzeptiert hat, kann man Dekohärenz natürlich problemlos in ihre Begriffswelt einfügen. Es ist aber nicht richtig zu behaupten, daß dies die MWI bestätigen würde. Dekohärenz funktioniert genauso gut auf Ensembles.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Wenn ich eine statistisch unbestimmte Wechselwirkung mit der Umgebung bräuchte, damit Zweige überhaupt entstehen, existierten keine Zweige im Universum, denn dieses hat keine Umgebung, mit der es wechselwirken kann. Die Zweige wären dann also kein fundamentales Konzept, sondern ein thermodynamisches. |
Ich denke, ich weiß, worauf du hinauswillst, auch wenn die Wortwahl ungeschickt ist.
|
Überhaupt nicht. Diese partielle "Ausspuren", von dem du gleich sprichst, ist doch genau die statistische Grundlage, auf der die bekannten thermodynamische Ensembles eingeführt werden. Beim kanonischen Ensemble bildet man die partielle Spur über das Wärmebad, beim großkanonischen über das Wärme- und Teilchenbad, im allgemeinen eben über die (nicht näher spezifizierte) "Umgebung" des Systems. "Thermodynamisch" trifft es ganz gut, finde ich.
| Zitat: |
Ja, die Zweige resultieren aus Beobachtersicht letztlich daraus, dass er die Umgebungsfreiheitsgrade nicht sämtlich beobachten kann. Dies führt zu einem „Ausspuren der Umgebungsfreiheitsgrade“ und zum Auftreten der Zweige. Wäre ein Beobachter in der Lage, alle Freiheitsgrade zu beobachten, würde er keine klassische Welt beobachten, sondern immer den vollen quantenmechanischen Zustand inklusive aller Superpositionen und Verschränkungen.
|
Das soll noch was mit Everett zu tun haben? Das steht in klarem Widerspruch zu dem was er schreibt.
Ich halte es auch für eine Scheinlösung. Im Prinzip sagst du ja, das Axiom, nach dem bei einer Messung stets ein Eigenwert mit einer gewissen Wahrscheinlichkeit auftritt sei nur eine Näherung an Situationen, in denen eine Wechselwirkung mit Systemen mit einer großen Anzahl Freiheitsgrade stattfindet. Das deckt aber nicht alle Fälle ab. Also ist es aus Sicht der Interpretation unbefriedigend, es sei denn du meinst die QM gälte nur für solche Systeme, in denen ich zwischen mikroskopischem System und makroskopischem Beobachter+Umgebung unterscheiden kann.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zitat: | | Korrektur: die Everett-I. postuliert diese Zweige nicht, sie akzeptiert ihre Realität als Folgerung des Formalismus. Das ist mathematisch kein Unterschied, jedoch philosophisch bzw. axiomatisch ein ganz erheblicher. Die Everett-I. ist logisch konsistent, axiomatisch sparsam (im Sinne von Ockham). |
Was keine Folgerung ist, sollte man ehrlicherweise auch nicht als Folgerung bezeichnen.
[...]
|
Sorry, aber du argumentierst unsauber.
Ich sage nicht, dass die Realität der Zweige aus dem Formalismus folgt. Ich sage lediglich, dass die Zweige aus dem Formalismus folgen (und das tut sie unzweifelhaft im mathematischen Sinn), und dass ich ihre Existenz als real akzeptiere (d.h. kein zusätzliches Axiom oder Postulat einführe, um sie wegzudiskutieren).
|
Tut mir leid, selbst bei aller Sympathie für spitzfindige Argumente, kann ich das nicht ernst nehmen. Da steht fast wörtlich, die MWI akzeptiere die Realität der Zweige als Folgerung aus dem Formalismus. Anders konnte man das kaum verstehen. Deine jetzigen Erläuterungen lassen es höchstens noch unklarer werden, wie du denn nun eigentlich verstanden werden wolltest.
Was folgt unzweifelhaft mathematisch aus dem Formalismus der QM? Daß eine Linearkombination aus mehreren Summanden bestehen kann? Daß man diese Summanden "Zweige" taufen kann?
Und worauf genau soll die Andeutung anspielen, es würden zusätzliche Postulate eingeführt um die reale Existenz von irgendetwas "wegzudiskutieren"? Gibt es in der Ensembleinterpretation oder irgendeiner anderen Interpretation das Axiom "Es existieren in der Realität keine Zweige"? Leugnet die Ensembleinterpretation das Auftreten von Superpositionen oder daß man sie in der Form \rangle |f(a)\rangle) schreiben kann? Nichts an diesem Formalismus suggeriert auch nur die reale Existenz von Zweigen im Sinne der MWI. In diesem Zusammenhang das Wort "Folgerung" zu benutzen ist, gelinde gesagt, unangebracht. schreiben kann? Nichts an diesem Formalismus suggeriert auch nur die reale Existenz von Zweigen im Sinne der MWI. In diesem Zusammenhang das Wort "Folgerung" zu benutzen ist, gelinde gesagt, unangebracht.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zweitens sehe ich im Augenblick auch ein logisches Problem, den Zweigen einen Produktzustand |a, relativ zu B>|B> zuzuordnen, der aus einem definitiven Beobachterzustand |B> und dem dazu relativen Systemzustand besteht, welches mir nicht lösbar erscheint … |
Klingt nach einem spannenden Argument, ich versteh’s aber nicht.
|
Das ist ganz einfach. Zwei Teilsysteme im initialen Produktzustand \left(\sum_b v_b|b , 0\rangle\right)) wechselwirken miteinander auf eine Weise, wie es der Definition von "Messung" im Sinne von Everett enstpricht. a und b sind jeweils die zu messenden Eigenschaften, die null bezeichnet den ready-state der Indikatorvariable. Nach der Messung befinde sich das System folglich im Zustand wechselwirken miteinander auf eine Weise, wie es der Definition von "Messung" im Sinne von Everett enstpricht. a und b sind jeweils die zu messenden Eigenschaften, die null bezeichnet den ready-state der Indikatorvariable. Nach der Messung befinde sich das System folglich im Zustand
\rangle|b, g(a)\rangle)
Welche Zweige sind entstanden und in welchem Zustand befinden sie sich? Die Frage nach dem Zustand muß m.E. beantwortbar sein, sofern die Zweige real existieren und die Everettsche Interpretation eine realistischen Beschreibung der Situation liefern kann.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ich habe gerade eben noch gelernt, daß eine Verallgemeinerung dieses Arguments offenbar als "Basisproblem" bekannt ist. Die einzig bekannte Lösung scheint Dekohärenz zu sein. Die greift allerdings nicht, wenn es um die fundamentale Frage der Realität der Zweige geht. Sie liefert nur die "Zweighaftigkeit" von Systemen im thermodynamischen Grenzwert. Das ist m.E. zu wenig. |
Ja, das ist aber auch nicht der Anspruch der Dekohärenz.
|
Aber der Anspruch der MWI. Oder existieren die Zweige doch nicht real oder nur näherungsweise?
| Zitat: |
Zunächst löst die Dekohärenz nach gängiger Meinung (es gibt aber m.W.n. vereinzelte Gegenstimmen) das Problem der „preferred basis“. Dann sie löst das Problem, warum klassische bzw. „zweighafte“ Systeme resultieren. Darin eingeschlossen ist die wechselweise Unbeobachtbarkeit dieser Zweige (ich denke wieder, dass „thermodynamischer Grenzwert“ nicht der treffende Ausdruck ist; es geht um das Ausspuren praktisch unbeobachtbarer Umgebungsfreiheitsgrade).
|
Dieses "Ausspuren" definiert praktisch ja ein thermodynamisches Ensemble. Der Limes garantiert nur die Kleinheit der relativen Schwankungen und damit die Äquivalenz der Ensembles. Ansonsten ging es mir nicht um die Frage was Dekohärenz leistet, sondern was die MWI leistet.
| Zitat: |
Die Dekohärenz löst das Problem der Realität dieser Zweige tatsächlich nicht. Das ist auch nicht möglich, da die Dekohärenz schlichtweg eine mathematische Folgerung des Formalismus darstellt, nicht dessen Interpretation. Zusätzlich zur Dekohärenz kommen nun Interpretationen ins Spiel. Manche davon besagen, dass nur ein Zweig real existent bleibt. Andere besagen, dass wir ab der Messung nur noch den Zweig für weitere Berechnungen verwenden sollen, der dem gemessen Ergebnis entspricht. Die Everettsche I. besagt, dass alle Zweige real existent bleiben.
|
Dann verstehe ich nicht, warum du Dekohärenz überhaupt ins Spiel gebracht hast. Es ging ausschließlich um die Interpretationen und insbesondere die Realität der Zweige. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Sep 2015 20:33 Titel: index_razor Verfasst am: 01. Sep 2015 20:33 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Gegeben sei ein Produkthilbertraum "Quantensystem * Messgerät * Umgebung" sowie die unitäre Zeitentwicklung im Kontext einer "Messung (= Interaktion des Quantensystems mit dem Messgerät sowie mit der Umgebung) gem. Schrödungergleichung:
\,|0\rangle\,|E\rangle \;\to\; (|a\rangle\,|A\rangle + |b\rangle\,|B\rangle)\,|E^\prime\rangle + \ldots)
Die Dekohärenz besagt, dass aus dieser Interaktion eine Zweigstruktur dergestalt resultiert, dass die mikroskopische Superposition |a> + |b> im Eingangszustand zu einer makroskopischen Superposition |aA...> + |bB...> + ... im Endzustand führt. Jede Komponente |aA...>, ... des Gesamtzustandes repräsentiert einen "Zweig". Diese Zweige sind jeweils stabil und wechselweise unsichtbar. Die Dekohärenz erklärt demnach, wie und warum makroskopische "Zeigerzustände" |aA>, ... resultieren und warum wir nur diese wahrnehmen, d.h. warum erstens die Superposition an sich unsichtbar ist und (beoachter-lokal) nur ein Zweig sichtbar ist, und warum zweitens nicht-diagonale Komponenten der Form |aB> dynamisch unterdrückt und damit unsichtbar sind.
|
Das hat doch noch gar nichts mit Dekohärenz zu tun. Die Form |aA> + |bB> + ... folgt einfach aus der unitären Zeitentwicklung. Terme |aB> treten laut Voraussetzung nicht auf, wenn es sich beim zweiten System um ein Meßgerät für die Observable a des ersten handelt. Die Dekohärenz beantwortet nur die Frage warum im statistischen Operator von System+Meßgerät keine Terme der Form |aA><bB| mehr auftreten. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 02. Sep 2015 07:53 Titel: bassiks Verfasst am: 02. Sep 2015 07:53 Titel: |
 |
|
| Zitat: | | Mein hypothetischer "Ensemble-Ontologe" kann genauso behaupten, es existieren nicht viele reale Welten, sondern nur eine, aber diese sei ein Ensemble. |
Wie darf man das verstehen? Eine "Welt" soll ein Ensemble sein?
| Zitat: | | n seiner Sichtweise zwingt uns natürlich genau die Tatsache, daß der Zustand eine Wahrscheinlichkeitsamplitude beschreibt, die reale Existenz von Ensembles anzunehmen. Du bezeichnest die Ensembles als "gedacht", aber nur wegen deiner ontologischen Vorurteile. Du denkst auch nur, daß du ein einzelnes System präparierst, stattdessen ensteht immer ein Ensemble (Teilensemble eines großen Universumsensembles). |
Meines Wissens nach ist genau das aber nicht so in der Ensemble-Interpretation. Bei der Betrachtung eines Teilchens benutzt die Ensemble-Interpretation ein gedachtes Ensemble an Teilchen. Sie macht m.E nach keine Aussage über einzelne "Teilchen". Der Vorteil der Ensemble Interpretation gegenüber der kop. Deutung ist für mich lediglich, dass sie den Kollaps vermeidet indem sie festlegt, dass ein einzelnes System sich nicht in einer Superposition befinden kann.
Wenn du aber nun behauptest du könntest die Existenz der Ensembles als real annehmen, dann stellt sich mir die Frage wie du deinen Formalismus erweiterst? Denn nach einer Messung habe ich es (sofern man die Ensembles als real ansieht) einen Vertreter dieses Ensembles vor mir. Wie wird daraus wieder ein Ensemble? Wenn die Ensembles real sind, was sind die verborgenen Parameter welche wir ignorieren oder nicht kennen (ähnlich den einzelnen Orten und Impulsen der Teilchen in einem Gas) ?
Ich habe verstanden dass du nicht hier bist um die Ensemble-Interpretation zu verteidigen, aber du hast behauptet dass du die Ensembles als ebenso real ansehen kannst wie es die E.I mit den Zweigen tut, und das denke ich nicht.
Meiner Meinung nach ist der Begriff "Many Worlds" ungünstig, denn der Begriff Worlds ist etwas schwammig. Ich sehe das so: Akzeptiert man den Zustand als das was real existiert, dann ist die real existierende Welt ein einziger Zustand, welcher eine Superposition aus den möglichen von einem in diesem Zustand lebenden Beobachter wahrgenommenen Zuständen ist.
Insofern ist die E.I sehr einfach, sie behauptet nicht der Zustand sei eine Beschreibung, sie gesteht ihm reale Existenz zu.
| Zitat: | Ich wollte dir nur mitteilen, daß ich die Probleme an anderer Stelle sehe. Egal ob ich die Wahrscheinlichkeiten postuliere oder ableite -- wenn ich sie erstmal in den Grundstrukturen (Zustand) der Theorie habe, entsteht sofort das Problem zu interpretieren, was beim Meßvorgang real passiert. Daran änderte sich überhaupt nichts, wenn bewiesen wäre, daß ich Wahrscheinlichkeiten unbedingt einführen muß.
Zitat:
Alle Interpretationen außer der Everettschen leben mit der Einführung von Wahrscheinlichkeiten per Postulat / Axiom.
Selbst wenn es stimmte, es ist vollkommen unerheblich. Die Frage ob ich die Wahrscheinlichkeiten in der Theorie postulieren muß oder ableiten kann, ist eine rein logische und hat mit der Interpretation nicht das geringste zu tun. Ich kann einfach alle logischen Beziehungen zwischen allen wahren Aussagen der QM ignorieren, sie alle wie Postulate behandeln und habe exakt gar nichts am Interpretationsproblem geändert. Es existiert genau wie vorher. |
Da stimme ich dir teilweise zu. Gesteht man dem Zustand nämlich reale Existenz zu, so ist die Theorie vollkommen deterministisch. Dennoch beobachten wir bei Messungen statistische Häufigkeiten. Um dies zu erklären könnte ich natürlich ein Axiom einführen, welches besagt, dass ich mit der Wahrscheinlichkeit p(a) ein Beobachter aus einem "Zweig" bin, in welchem mein Messgerät a ausspuckt. Eleganter/Schöner/Befriedigender wäre es aber wenn das Auftreten von Wahrscheinlichkeiten aus der Interpretation folgen würde. (Der Link von TomS zu diesem Thema ist äußerst lesenswert an dieser Stelle)
| Zitat: | | Sie behauptet zwar einfach ein Zustand beschreibe viele Welten, kann aber außerhalb gewisser Näherungen nicht eindeutig sagen, in welchem Zustand sich diese Welten befinden. |
Meiner Meinung nach kann sie das, sie kann dir nur nicht sagen welcher Beobachter du bist und in welcher dieser "Welten" (ich mag den Begriff nicht  ) du bist. ) du bist.
| Zitat: | Mißverständnis? Ich habe nicht gesagt, daß ich die MWI oder ihre Vetreter nicht ernst nehme. Ich behaupte nur, daß ihre Vertreter, zumindest sofern sie dieses Glaubensbekenntnis als Lösung des Meßproblems ansehen, das Meßproblem nicht besonders ernstnehmen.
|
Ich denke schon dass sie das tun, denn sonst wären sie nicht so bemüht die Wahrscheinlichkeit nicht per Axiom einzuführen.
| Zitat: | | Ich meine mit Phänomen die Tatsache, daß bei jeder Einzelmessung genau ein Meßwert auftaucht. Dies ist erst dann ein Problem, wenn meine vollständige Beschreibung des Systems Wahrscheinlichkeiten enthält. Die fleißigen Bemühungen diese Wahrscheinlichkeiten abzuleiten, können dieses Problem nicht lösen, sondern nur zeigen, daß es notwendig auftritt. |
Genau. Die E.I ist deterministisch, sie erklärt also warum nur ein Messwert aufrtitt. Wir beobachten aber statistische Häufigkeiten, es wäre also schön wenn man mit der E.I auch diese erklären könnte ohne sie einfach zu postulieren.
| Zitat: |
Dekohärenz liefert mir nur in bestimmten Situationen eine plausible realistische Erklärung für dieses Phänomen. Nämlich sofern man sinnvoll behaupten kann: Der Meßwert a erscheint mit der Wahrscheinlichkeit p(a), da sich das System mit derselben Wahrscheinlichkeit in einem Zustand befindet, in dem a mit Sicherheit auftritt. Aber gerade dieser Fall funktioniert zumindest in der Ensembleinterpretation genauso gut. Die Fälle, in denen dies nicht geht sind deshalb die aus Sicht der Interpretation interessanten. |
Kannst du hierzu evt. ein Beispiel bringen?
| Zitat: | | Aus genau diesem Grund halte ich "System = Ensemble" für nicht besonders befriedigend. System = Menge von Zweigen ist allerdings genauso wenig überzeugend, denn den Zweigen kann nicht unter allen Umständen reale Existenz zugesprochen werden. In den Fällen, in denen es geht, habe ich auch ein statistisches Ensemble. |
Wann darf ich den "Zweigen" keine reale Existenz zuschreiben?
| Zitat: |
Klar, wenn man die MWI einmal akzeptiert hat, kann man Dekohärenz natürlich problemlos in ihre Begriffswelt einfügen. Es ist aber nicht richtig zu behaupten, daß dies die MWI bestätigen würde. Dekohärenz funktioniert genauso gut auf Ensembles.
|
Ja, aber für eine ernst zu nehmende Interpretation wäre es gut mit der Dekohärenz kompatibel zu sein.
| Zitat: | | Dann verstehe ich nicht, warum du Dekohärenz überhaupt ins Spiel gebracht hast. Es ging ausschließlich um die Interpretationen und insbesondere die Realität der Zweige. |
Ich denke er hat dies getan, da das Problem der gängigen Interpretationen das Messproblem ist, und die Dekohärenz die Lösung eines Teils dieses Problems darstellt. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Sep 2015 11:54 Titel: index_razor Verfasst am: 02. Sep 2015 11:54 Titel: |
 |
|
| bassiks hat Folgendes geschrieben: | | Zitat: | | Mein hypothetischer "Ensemble-Ontologe" kann genauso behaupten, es existieren nicht viele reale Welten, sondern nur eine, aber diese sei ein Ensemble. |
Wie darf man das verstehen? Eine "Welt" soll ein Ensemble sein?
|
Genau diese Frage stelle ich in Bezug auf die MWI: Wie darf ich mir vorstellen, daß eine einzelne Katze eine Superposition von Zweigen ist? Zu nichts anderem diente dieses Beispiel. Ich behaupte nicht die Welt sei ein Ensemble, sondern daß diese Behauptung genauso sinnvoll ist wie die analoge der MWI, die Welt sei eine Menge real existierender Zweige.
| Zitat: |
| Zitat: | | n seiner Sichtweise zwingt uns natürlich genau die Tatsache, daß der Zustand eine Wahrscheinlichkeitsamplitude beschreibt, die reale Existenz von Ensembles anzunehmen. Du bezeichnest die Ensembles als "gedacht", aber nur wegen deiner ontologischen Vorurteile. Du denkst auch nur, daß du ein einzelnes System präparierst, stattdessen ensteht immer ein Ensemble (Teilensemble eines großen Universumsensembles). |
Meines Wissens nach ist genau das aber nicht so in der Ensemble-Interpretation. Bei der Betrachtung eines Teilchens benutzt die Ensemble-Interpretation ein gedachtes Ensemble an Teilchen. Sie macht m.E nach keine Aussage über einzelne "Teilchen".
|
Was ist nicht wie? Das sage ich doch. Die Ensembleinterpretation macht keine Aussagen über Einzelsysteme (im gewöhnlichen Sinne des Wortes, nicht in dem verqueren Sinn des "Ensemble-Ontologen").
Welche spezifischen, insbesondere quantitativen Aussagen macht denn die MWI über einzelne Systeme? Außer dem Glaubenssatz, daß sich dieses einzelne System wahrhaftig in dem Zustand befindet, den es laut QM-Formalismus haben sollte, nicht viel. Alles andere sind Wahrscheinlichkeitsaussagen.
| Zitat: |
Der Vorteil der Ensemble Interpretation gegenüber der kop. Deutung ist für mich lediglich, dass sie den Kollaps vermeidet indem sie festlegt, dass ein einzelnes System sich nicht in einer Superposition befinden kann.
Wenn du aber nun behauptest du könntest die Existenz der Ensembles als real annehmen, dann stellt sich mir die Frage wie du deinen Formalismus erweiterst?
|
Erweiterungen des Formalismus braucht man dafür nicht, das ist nur eine Interpretationsfrage. In Anlehnung an die MWI: "Der Ensemble-Ontologe GLAUBT im Sinne einer philosophischen Überzeugung, daß das System ein Ensemble IST."
| Zitat: |
Denn nach einer Messung habe ich es (sofern man die Ensembles als real ansieht) einen Vertreter dieses Ensembles vor mir. Wie wird daraus wieder ein Ensemble?
|
Nein, du mußt das Gesamtsystem betrachten. Das ist sowohl vor als auch nach der Messung immer ein Ensemble, beschrieben durch den Zustand
\rangle)
Die einzelnen Vertreter dieses Ensembles sind wiederum Ensembles beschrieben durch bedingte Wahrscheinlichkeitsamplituden
|B(a)\rangle,)
deren Koeffizienten 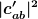 die bedingte Wahrscheinlichkeit angeben bei einer (weiteren) Messung den Wert b zu erhalten wenn der Beobachter den Wert a gemessen hat. die bedingte Wahrscheinlichkeit angeben bei einer (weiteren) Messung den Wert b zu erhalten wenn der Beobachter den Wert a gemessen hat.
Im Endzustand ist nur noch das beobachtete System in einem echten Ensemble. Der Beobachter |B(a)> stellt einen wohldefinierten Vertreter aus dem ursprünglichen Ensemble dar. Die Situation ist völlig analog zur MWI.
| Zitat: |
Wenn die Ensembles real sind, was sind die verborgenen Parameter welche wir ignorieren oder nicht kennen (ähnlich den einzelnen Orten und Impulsen der Teilchen in einem Gas) ?
|
Das würde ich auch gern wissen. Das betrachtet der Ensemble-Ontologe natürlich auch ganz ehrlich als offenes Problem, und es ist seiner Meinung nach der einzig wirkliche Grund, aus dem man die Ensemble-Interpretation kritisieren kann. Die Ensemble-Ontologen bemühen sich aber fleißig, diese verborgenen Parameter aufzuspüren. Derartige ungelöste Probleme kommen ja schließlich in den besten Interpretationen vor. Aber die Ensemble-Interpretation leistet ja auch so schon eine Menge: Sie räumt mit dem uralten Vorurteil auf es gäbe sowas wie ein "einzelnes Teilchen". In Wirklichkeit gibt es ontologisch nur Ensembles. Einzelne Teilchen erscheinen einem höchstens mal, wenn die vielen Freiheitsgrade der Umgebung Dekohärenz bewirkt haben. Damit ist die Dekohärenz ein starkes Indiz für die Ensembleinterpretation, denn erst mit Dekohärenz kann man wirklich verstehen, was ein Ensemble mit dem Phänomen "einzelnes Teilchen" zu tun hat. etc. etc.
| Zitat: |
Ich habe verstanden dass du nicht hier bist um die Ensemble-Interpretation zu verteidigen, aber du hast behauptet dass du die Ensembles als ebenso real ansehen kannst wie es die E.I mit den Zweigen tut, und das denke ich nicht.
|
Doch, ich denke schon (s.o.)
| Zitat: |
Meiner Meinung nach ist der Begriff "Many Worlds" ungünstig, denn der Begriff Worlds ist etwas schwammig. Ich sehe das so: Akzeptiert man den Zustand als das was real existiert, dann ist die real existierende Welt ein einziger Zustand, welcher eine Superposition aus den möglichen von einem in diesem Zustand lebenden Beobachter wahrgenommenen Zuständen ist.
Insofern ist die E.I sehr einfach, sie behauptet nicht der Zustand sei eine Beschreibung, sie gesteht ihm reale Existenz zu.
|
Die Welt ist ein Zustand? Ich finde da geht einiges durcheinander. Ich weiß nicht so richtig wie ich das ordnen soll.
Ich versuch's mal. Wir sind ja keine Profi-Philosophen, deswegen mache ich mir mal keine Sorgen allzu naiv zu klingen: Also, auf der einen Seite haben wir die Realität. Die ist halt so wie sie ist. Auf der anderen Seite sind unsere theoretischen Aussagen über diese Realität. Aus letzteren entspringt die Wellenfunktion. Die Wellenfunktion ist Teil von Aussagen über den Zustand real existierender Objekte. Diese Aussagen erscheinen je nach Situation nun leider etwas unspezifisch. ("Die Wahrscheinlichkeit für den Meßwert a eines Systems im Zustand mit der Wellenfunktion soundso ist soundo.") Die Frage ist einfach, was bedeutet das? Ist die Realität unspezifisch oder ist unsere Beschreibung unvollständig? Oder ist die Beschreibung vollständig, betrifft aber nicht das System, sondern das, was wir maximal über das System wissen können? Wenn ja, wer ist "wir"? Menschen? Oder auch Aliens und intelligente Computer? etc.
Mir ist nun nicht so klar, wie ihr euch vorstellt, daß die MWI diese Problem gelöst haben soll. Aussagen wie "das System ist der Zustand" ergeben keinen Sinn oder sind völlig trivial. Sinnlos ist es zu behaupten, das System sei der Zustandsvektor. Das ist genausowenig der Fall, wie das Wort "Auto" ein Auto ist. Dann bleibt: "Das System ist das, was der Zustand beschreibt." Das ist trivial. Stell dir vor, du erhältst einen Brief mit dem Inhalt "asla lksazwuwu laksjdlas lakskdsla" und fragst dich was das bedeuten soll. Jemand sagt dir, er habe dieses Problem für dich gelöst: Seiner festen philosophischen Überzeugung nach ist die Aussage in der Nachricht wahr. Und sie drückt genau den Sachverhalt aus, daß eben asla lksazwuwu laksjdlas lakskdsla. Fühlst du dich jetzt schlauer oder ernst genommen? Wenn du jetzt sagst, daß dir das keinen Deut weiterhilft und daß man ja normalerweise die Bedeutung einer Aussage nicht aus ihrem vorausgesetzten Wahrheitsgehalt erschließt, sondern umgekehrt, wird erwidert: "Ja, ja, aber es ist eben meine philosophische Überzeugung, daß Nachrichten eine Bedeutung haben sollten und nicht einfach nur Kauderwelsch enthalten. Aber wenn du diese Überzeugung nicht teilst, bist du ja vielleicht der Meinung, daß man sich auch nur auf das Lesen der Zeichenketten beschränken kann, und man den Inhalt gar nicht so genau verstehen müsse. Dann hast du eben einfach geringere Ansprüche an den Inhalt von Nachrichten..." Das ist so in etwa die Situation in der Interpetationsdiskussion. ;-)
| Zitat: |
| Zitat: | Ich wollte dir nur mitteilen, daß ich die Probleme an anderer Stelle sehe. Egal ob ich die Wahrscheinlichkeiten postuliere oder ableite -- wenn ich sie erstmal in den Grundstrukturen (Zustand) der Theorie habe, entsteht sofort das Problem zu interpretieren, was beim Meßvorgang real passiert. Daran änderte sich überhaupt nichts, wenn bewiesen wäre, daß ich Wahrscheinlichkeiten unbedingt einführen muß.
Zitat:
Alle Interpretationen außer der Everettschen leben mit der Einführung von Wahrscheinlichkeiten per Postulat / Axiom.
Selbst wenn es stimmte, es ist vollkommen unerheblich. Die Frage ob ich die Wahrscheinlichkeiten in der Theorie postulieren muß oder ableiten kann, ist eine rein logische und hat mit der Interpretation nicht das geringste zu tun. Ich kann einfach alle logischen Beziehungen zwischen allen wahren Aussagen der QM ignorieren, sie alle wie Postulate behandeln und habe exakt gar nichts am Interpretationsproblem geändert. Es existiert genau wie vorher. |
Da stimme ich dir teilweise zu. Gesteht man dem Zustand nämlich reale Existenz zu, so ist die Theorie vollkommen deterministisch.
|
Das deterministische ist die Schrödingergleichung. Deren Determinismus ist noch völlig unabhängig von der Interpretation.
| Zitat: |
Dennoch beobachten wir bei Messungen statistische Häufigkeiten. Um dies zu erklären könnte ich natürlich ein Axiom einführen, welches besagt, dass ich mit der Wahrscheinlichkeit p(a) ein Beobachter aus einem "Zweig" bin, in welchem mein Messgerät a ausspuckt. Eleganter/Schöner/Befriedigender wäre es aber wenn das Auftreten von Wahrscheinlichkeiten aus der Interpretation folgen würde. (Der Link von TomS zu diesem Thema ist äußerst lesenswert an dieser Stelle)
|
Ich kann nur wiederholen, daß ich nicht der Meinung bin, daß dies irgendwas mit dem Problem zu tun hat. Sicher will ich aus Eleganzgründen ein minimales Axiomensystem, aber das ist nicht das Thema. Das Thema ist, was Wahrscheinlichkeitsaussagen in einer vollständigen Theorie bedeuten, nicht woraus sie logisch folgen.
| Zitat: |
| Zitat: | | Sie behauptet zwar einfach ein Zustand beschreibe viele Welten, kann aber außerhalb gewisser Näherungen nicht eindeutig sagen, in welchem Zustand sich diese Welten befinden. |
Meiner Meinung nach kann sie das, sie kann dir nur nicht sagen welcher Beobachter du bist und in welcher dieser "Welten" (ich mag den Begriff nicht  ) du bist. ) du bist.
|
Dann geht diese Frage hier an dich:
| index_razor hat Folgendes geschrieben: |
Zwei Teilsysteme im initialen Produktzustand \left(\sum_b v_b|b , 0\rangle\right)) wechselwirken miteinander auf eine Weise, wie es der Definition von "Messung" im Sinne von Everett enstpricht. a und b sind jeweils die zu messenden Eigenschaften, die null bezeichnet den ready-state der Indikatorvariable. Nach der Messung befinde sich das System folglich im Zustand wechselwirken miteinander auf eine Weise, wie es der Definition von "Messung" im Sinne von Everett enstpricht. a und b sind jeweils die zu messenden Eigenschaften, die null bezeichnet den ready-state der Indikatorvariable. Nach der Messung befinde sich das System folglich im Zustand
\rangle|b, g(a)\rangle)
Welche Zweige sind entstanden und in welchem Zustand befinden sie sich?
|
| Zitat: |
| Zitat: | Mißverständnis? Ich habe nicht gesagt, daß ich die MWI oder ihre Vetreter nicht ernst nehme. Ich behaupte nur, daß ihre Vertreter, zumindest sofern sie dieses Glaubensbekenntnis als Lösung des Meßproblems ansehen, das Meßproblem nicht besonders ernstnehmen.
|
Ich denke schon dass sie das tun, denn sonst wären sie nicht so bemüht die Wahrscheinlichkeit nicht per Axiom einzuführen.
|
Wie gesagt, spielt es keine Rolle woher die Wahrscheinlichkeiten kommen. Mit den Wahrscheinlichkeiten fangen die Probleme erst an. Glaubensbekenntnisse über die reale Existenz dessen was der Zustand beschreibt, lösen sie nicht.
| Zitat: |
| Zitat: | | Ich meine mit Phänomen die Tatsache, daß bei jeder Einzelmessung genau ein Meßwert auftaucht. Dies ist erst dann ein Problem, wenn meine vollständige Beschreibung des Systems Wahrscheinlichkeiten enthält. Die fleißigen Bemühungen diese Wahrscheinlichkeiten abzuleiten, können dieses Problem nicht lösen, sondern nur zeigen, daß es notwendig auftritt. |
Genau. Die E.I ist deterministisch, sie erklärt also warum nur ein Messwert aufrtitt. Wir beobachten aber statistische Häufigkeiten, es wäre also schön wenn man mit der E.I auch diese erklären könnte ohne sie einfach zu postulieren.
|
Nein, sie erklärt nicht, warum nur ein Meßwert auftritt. Das deterministische in der QM (egal welcher Interpretation) ist die Schrödingergleichung, also die Zeitentwicklung des Zustands. In der MWI beschreibt dieser Zustand alle Zweige, d.h. seine Zeitentwiklung beinhaltet stets alle möglichen auftretenden Meßwerte. Welcher Meßwert im einzelnen auftritt oder warum nur einer auftritt, kann sie dir nicht genauer sagen, als die Ensembleinterpretation.
| Zitat: | | Zitat: |
Dekohärenz liefert mir nur in bestimmten Situationen eine plausible realistische Erklärung für dieses Phänomen. Nämlich sofern man sinnvoll behaupten kann: Der Meßwert a erscheint mit der Wahrscheinlichkeit p(a), da sich das System mit derselben Wahrscheinlichkeit in einem Zustand befindet, in dem a mit Sicherheit auftritt. Aber gerade dieser Fall funktioniert zumindest in der Ensembleinterpretation genauso gut. Die Fälle, in denen dies nicht geht sind deshalb die aus Sicht der Interpretation interessanten. |
Kannst du hierzu evt. ein Beispiel bringen?
|
Zeitentwicklung eines abgeschlossenen Systems oder generell eines, in dem keine "einselection" auftritt. Siehe oben für ein Beispiel.
| Zitat: |
| Zitat: | | Aus genau diesem Grund halte ich "System = Ensemble" für nicht besonders befriedigend. System = Menge von Zweigen ist allerdings genauso wenig überzeugend, denn den Zweigen kann nicht unter allen Umständen reale Existenz zugesprochen werden. In den Fällen, in denen es geht, habe ich auch ein statistisches Ensemble. |
Wann darf ich den "Zweigen" keine reale Existenz zuschreiben?
|
"Darf"? Wenn du es kannst, darfst du natürlich. Bevor man etwas als real existent bezeichnet, sollte man aber eine realistische, einigermaßen spezifische Beschreibung davon abliefern können. (So wie die Mikrozustände in der klassischen statistischen Mechanik.) Im Kontext der QM erwarte ich zumindest eine eindeutige Angabe des Zustands.
| Zitat: | | Zitat: |
Klar, wenn man die MWI einmal akzeptiert hat, kann man Dekohärenz natürlich problemlos in ihre Begriffswelt einfügen. Es ist aber nicht richtig zu behaupten, daß dies die MWI bestätigen würde. Dekohärenz funktioniert genauso gut auf Ensembles.
|
Ja, aber für eine ernst zu nehmende Interpretation wäre es gut mit der Dekohärenz kompatibel zu sein.
|
Ja natürlich, was alle gängigen Interpretationen auch sind. Also ist Dekohärenz irrelevant, wenn es um den Vergleich verschiedener Interpretationen geht.
| Zitat: |
| Zitat: | | Dann verstehe ich nicht, warum du Dekohärenz überhaupt ins Spiel gebracht hast. Es ging ausschließlich um die Interpretationen und insbesondere die Realität der Zweige. |
Ich denke er hat dies getan, da das Problem der gängigen Interpretationen das Messproblem ist, und die Dekohärenz die Lösung eines Teils dieses Problems darstellt. |
Möglicherweise. Aber es ergibt keinen Sinn, die Dekohärenz als Indiz für eine bestimmte Interpretation heranzuziehen, auf der Grundlage, daß diese mit der Dekohärenz genauso verträglich ist, wie alle anderen Interpretationen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 02. Sep 2015 12:36 Titel: TomS Verfasst am: 02. Sep 2015 12:36 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Du argumentierst zirkulär. Die Frage womit wir es in der realen Welt zu tun haben, ist genau jene, die die Interpretation (bzw. deren Ontologie) beantworten soll. Also kannst du als Argument gegen eine Interpretation nicht anführen, was deiner vorgefaßten Meinung nach real existiert. |
Doch, das kann ich. Und das ist auch nicht zirkulär.
Der wesentliche Startpunkt bzgl. einer Interpretation ist immer auch eine philosophische Grundhaltung, die man aus der Physik heraus nicht ableiten kann. Wenn du eine Grundhaltung hast, die nicht zur Everett-I. passt, dann scheidet letztere eben gerade wegen dieser nicht weiter hinterfragbaren Grundhaltung aus.
| index_razor hat Folgendes geschrieben: | | Mein hypothetischer "Ensemble-Ontologe" kann genauso behaupten, es existieren nicht viele reale Welten, sondern nur eine, aber diese sei ein Ensemble. |
Ich halte deine Argumente auf Basis der Ensemble-I. in diesem Zusammenhang für insgs. nicht hilfreich, und gehe im Folgenden auch nicht näher darauf ein. Weiter unten werden wir sehen, was dein eigentliches Problem ist, und dafür benötigen wir diesen Vergleich nicht mehr.
| index_razor hat Folgendes geschrieben: | | Die Frage ob ich die Wahrscheinlichkeiten in der Theorie postulieren muß oder ableiten kann, ist eine rein logische und hat mit der Interpretation nicht das geringste zu tun. Ich kann einfach alle logischen Beziehungen zwischen allen wahren Aussagen der QM ignorieren, sie alle wie Postulate behandeln und habe exakt gar nichts am Interpretationsproblem geändert. Es existiert genau wie vorher. |
Verstehe ich nicht. Seit wann haben Logik und Interpretation nichts miteinander zu tun?
Du hast mit der Everett-I. eine reale, objektive, deterministische und vollständige Interpretation. Wenn du mit einer realen, objektiven, deterministischen und vollständigen Interpretation startest, dann kannst du Wahrscheinlichkeiten gar nicht zusätzlich einführen, da dies den Voraussetzungen explizit widersprechen würde. Du musst also entweder das Auftreten von Wahrscheinlichkeiten aus den Annahmen heraus ableiten bzw. motivieren, oder du musst bestimmte Annahmen aufgeben (die Ensemble-I. gibt zumindest die Annahme der Vollständigkeit auf: sie besagt, dass Wahrscheinlichkeiten aufgrund der Unkenntnis über das einzelne System auftreten, ganz so wie in der statistischen Mechanik; dieser Ausweg ist für die Ensemble-I. logisch konsistent möglich, er ist einer ihrer Wesenszüge; er ist jedoch völlig unmöglich für die Everett-I., da diese damit etwas fundamental anderes werden würde).
| index_razor hat Folgendes geschrieben: | | Die Newtonsche Mechanik macht auch sehr spezifische Angaben über die Zustände, in denen sich die Systeme innerhalb eines klassischen statistischen Ensembles befinden können: Sie sind eindeutig durch Orte und Impulse aller Teilchen, also Punkte im Phasenraum, spezifiziert, während das ganze Ensemble durch eine Wahrscheinlichkeitsverteilung über diesem Phasenraum charakterisiert ist. |
Richtig.
| index_razor hat Folgendes geschrieben: | | Die MWI hat genau mit dieser eindeutigen Spezifikation Probleme. Sie behauptet zwar einfach ein Zustand beschreibe viele Welten, kann aber außerhalb gewisser Näherungen nicht eindeutig sagen, in welchem Zustand sich diese Welten befinden. |
Falsch!
Sie behauptet, dass genau eine Welt mit einer Zweigstruktur existiert. Und diese Zweigstruktur ist eben gerade so gut berechenbar, wie die Gleichungen im Kontext der Dekohärenz lösbar sind (es ist heute sinnlos, ohne die Dekohärenz zu argumentieren).
Jetzt kommen wir zum Punkt:
| index_razor hat Folgendes geschrieben: | | Dein Satz über die Realität der Katze besagt doch nicht viel mehr, als "Was auch immer der Zustand eben beschreibt, das ist das reale System." Das hat nicht das geringste mit einer konkreten Interpretation zu tun. Derart rumtricksen kann man in jeder Interpretation. |
Doch, genau das ist die Interpretation!
Kleine Korrektur: "Was auch immer der Zustand eben beschreibt, das entspricht dem realen System." Das ist analog zur der Interpretation der Newtonschen Mechanik: „Was auch immer der Phasenraumzustand beschreibt, das entspricht dem realen System“.
Die Everett-I. bietet dir eine Ontologie, die rein strukturell zu einer naiven, realistischen, platonistischen Ontologie zurückführt. Das wird von ihren Vertretern als Vorteil gesehen. Der Preis dafür ist: du musst die tatsächliche Realität aller Zweige akzeptieren; und du musst verstehen, woher die subjektiven Wahrscheinlichkeiten resultieren.
| index_razor hat Folgendes geschrieben: | | Generell ist das Thema, ob eine Aussage der Theorie ein Axiom oder ein Theorem ist, von völlig untergeordneter Bedeutung. Eine Frage der Interpretation ist, was die Theorie, also die Gesamtheit ihrer Aussagen, bedeutet, nicht, welche ihrer Aussagen ich aus welchen ableiten kann. |
Dann arbeiten also alle Vertreter der Everett-I., die sich diesem Thema widmen, sowie alle Kritiker, die genau diese Arbeiten hinterfragen, an einem Scheinproblem. Sorry, aber deine Aussage ist absolut nicht ernst zu nehmen.
| index_razor hat Folgendes geschrieben: | | Ich habe nicht gesagt, daß ich die MWI oder ihre Vetreter nicht ernst nehme. Ich behaupte nur, daß ihre Vertreter, zumindest sofern sie dieses Glaubensbekenntnis als Lösung des Meßproblems ansehen, das Meßproblem nicht besonders ernstnehmen. |
Kannst du mal in eigenen Worten zusammenfassen, worin deiner Meinung nach das Messproblem besteht? Dann kann ich evtl. versuchen, zu erklären, inwiefern die Everett-I. (auf Basis der Dekohärenz) dieses Problem tatsächlich löst.
| index_razor hat Folgendes geschrieben: | | Wenn etwas am Thema vorbei geht, dann die unreflektierte Verwendung dieser beiden Begriffe als Synonyme. Aber es ist ja genau mein Vorwurf an dich, daß hinter der ganzen Ontologie der MWI, zumindest so wie du sie darstellst, nichts weiter steckt als diese nominelle Gleichsetzung: Es existiert genau das, was der Zustandsvektor eben beschreibt und das nennen wir "System". Daß dieses System aus realen Zweigen besteht, folgt bereits nicht mehr aus dem Formalismus .. |
Ich verwende nicht unreflektiert zwei Begriffe „System“ und „Zustandsvektor“ als Synonyme. Ich behaupte, dass im Rahmen der QM dem reale System ein Zustandsvektor im Hilbertraum entspricht. Eine Entsprechung im Sinne einer strukturellen Isomorphie ist keine Identität. Im Rahmen der naiven üblichen Interpretation Newtonschen Mechanik entspricht die mathematische Bahnkurve strukturell exakt der realen Bahnkurve eines Planeten.
Dein Vorwurf trifft mich gemeinsam mit Platon, Penrose u.v.a.m.; ich nehme das als Kompliment.
Und ja, völlig richtig, das ist die Ontologie der Everett-I.: Es existiert genau das, was der Zustandsvektor beschreibt.
Es ist richtig, die Aussage „dass dieses System aus realen Zweigen besteht, folgt nicht mehr aus dem Formalismus“ unterschreibe ich sofort. Das ist das Wesen dieser Interpretation und ihrer philosophischen Grundhaltung.
Wenn dir das alles nicht gefällt, dann ist das dein zentraler Kritikpunkt an dieser Interpretation, und dann sind alle weiteren Diskussionen bzgl. Wahrscheinlichkeiten usw. sekundär. Wenn du keinen Käse magst, ist es egal, ob es sich um Schweizer Emmentaler oder französischen Brie handelt.
| index_razor hat Folgendes geschrieben: | | Mehrere Zweige liegen "in der Praxis" auch nicht vor, sondern nur immer einer. |
Was meinst du mit „in der Praxis“?
Im Rahmen einer Messung sehe ich das Resultat exakt eines Zweiges nach der Messung. Im Rahmen der Berechnung (= der Vorhersage des zu erwartenden Ergebnisses der Messung) benötige ich jedoch zwingend alle Zweige (alle Komponenten = die gesamte Superposition) vor der Messung.
„In der Praxis“ liegen also vor der Messung sicher alle Komponenten vor, zumindest als mathematisches Modell.
Das einzige, was Everett jetzt getan hat, war, trivial und naiv anzunehmen, dass diese Zweige auch nach der Messung vorliegen, und dass sie real existent sind. So naiv das gewesen sein mag, so genial war das auch.
| index_razor hat Folgendes geschrieben: | | Was du siehst und was existiert sind zwei völlig verschiedene Dinge. Du siehst ja auch nicht beide Zweige deiner Superpositionskatze. Aber vielleicht verstehst du ja jetzt besser, was ich mit der Diskrepanz zwischen Phänomenen und Zustandsbeschreibung gemeint habe, da du das Argument hier ja jetzt selbst verwendet hast. |
Ich sehe diese Diskrepanz zwischen Phänomenen und Zustandsbeschreibung auch als Problem, und ich bin der Meinung, dass die Everett.-I sie in gewisser Weise löst. Die Everett-I. kann nämlich unter Zuhilfenahme der Dekohärenz tatsächlich erklären, warum das Phänomen (ein Messgerät, ein Eigenwert bzw. ein entsprechender Zeigerwert, eine tote Katze) und die Zustandsbeschreibung zwar unterschiedlich zu sein scheinen, jedoch logisch und strukturell verträglich sind.
Der wesentliche offene Punkte ist die Frage nach dem Auftreten von Wahrscheinlichkeiten (siehe Carroll, Wallace, Saunders, …). Aber das ist nicht dein wesentliches Problem mit dieser Interpretation; du hast offensichtlich schon früher prinzipielle Vorbehalte (s.o.)
| index_razor hat Folgendes geschrieben: | | Das "in der Praxis" gefällt mir gut. Ich dachte wir sprechen über Ontologie. In welchem Sinne liegen "in der Praxis" mehrere Zweige vor? |
s.o.: das mathematische Modell der QM enthält die Zweige trivialerweise im Rahmen einer Superposition.
| index_razor hat Folgendes geschrieben: | | Everett, Rev.Mod.Phys. 29 (1957). Darin ist natürlich von Dekohärenz nicht die Rede. Er wendet die Viele-Welten-Interpretation ausdrücklich auf geschlossenen Systeme in reinen Zuständen an, nicht auf Gemische. |
Das halte ich für unbefriedigend und inzwischen überholt.
| index_razor hat Folgendes geschrieben: | | Klar, wenn man die MWI einmal akzeptiert hat, kann man Dekohärenz natürlich problemlos in ihre Begriffswelt einfügen. Es ist aber nicht richtig zu behaupten, daß dies die MWI bestätigen würde. |
Ich habe auch nicht behauptet, dass die Dekohärenz die MWI bestätigt, sondern
| TomS hat Folgendes geschrieben: | | Die Dekohärenz löst das Problem der Realität dieser Zweige tatsächlich nicht. Das ist auch nicht möglich, da die Dekohärenz schlichtweg eine mathematische Folgerung des Formalismus darstellt, nicht dessen Interpretation ... Die Dekohärenz ist jedoch ein starkes Indiz dafür, dass die Everettsche I. sinnvoll ist, da sie sozusagen zur Hälfte die Arbeit bereits erledigt hat. Auf Basis der Dekohärenz scheint die Everettsche I. jedenfalls natürlicher zu sein als ohne sie. |
| index_razor hat Folgendes geschrieben: | | Im Prinzip sagst du ja, das Axiom, nach dem bei einer Messung stets ein Eigenwert mit einer gewissen Wahrscheinlichkeit auftritt sei nur eine Näherung an Situationen, in denen eine Wechselwirkung mit Systemen mit einer großen Anzahl Freiheitsgrade stattfindet. |
Ja, natürlich, genau das besagt die Everett-I. in Kombination mit der Dekohärenz. Insbs. enthält die Everettsche QM dieses Axiom überhaupt nicht!
| TomS hat Folgendes geschrieben: | Axiome:
1) Quantum states are represented by unit vectors in a separable Hilbert space.
2) Quantum states evolve in time according to the Schrödinger equation.
|
| index_razor hat Folgendes geschrieben: | | Oder existieren die Zweige doch nicht real oder nur näherungsweise? |
Die Zweige existieren gemäß dieser Interpretation real.
Ob es sinnvoll ist, das Wort „Zweig“ zu verwenden, hängt von den Gegebenheiten ab. Angewandt auf einen radioaktiven Atomkern würde man von einer Superposition sprechen; angewandt auf die arme Katze spricht man eben von „Zweig“, „Welt“ oder was auch immer. Mathematisch und nach Everett et al. ontologisch ist es das selbe.
Unter „Zweig“ verstehe ich hier Komponenten des Zustandsvektors, die gemäß der Dekohärenz wechselweise unsichtbar werden und diesbzgl. stabil sind. Letzteres ist insofern eine Näherung, als es nicht prinzipiell ausgeschlossen ist, durch immer bessere Experimente immer größere Systeme vollständig zu isolieren und zu messen, d.h. für immer größere Systeme die Zweighaftigkeit aufzulösen und die Interferenzfähigkeit wieder zurückzugewinnen. Bzgl. der Interpretation ändert das nichts..
| index_razor hat Folgendes geschrieben: | | Dann verstehe ich nicht, warum du Dekohärenz überhaupt ins Spiel gebracht hast. Es ging ausschließlich um die Interpretationen und insbesondere die Realität der Zweige. |
Darum:
| TomS hat Folgendes geschrieben: | Zunächst mal besteht das Messproblem aus mehrere Ebenen, die ich wie folgt skizzieren würde:
1) Messung im Gegensatz zu normaler Wechselwirkung
2) dynamische Selektion einer bestimmten Basis
3) Erscheinen wechselweise unsichtbarer quasiklassischer Zweige in dieser Basis
4) Anwendbarkeit von Wahrscheinlichkeiten auf Messreihen trotz einer fundamental deterministischen Theorie
1) wird trivialerweise gelöst durch die Axiomatik der Everettschen I. Es gibt schlichtweg nichts in den Axiomen oder dem Formalismus, was eine Messung von einer gewöhnlichen Wechselwirkung unterscheidet.
2) wird gelöst von der Dekohärenz; wenn ich die Observable A messe, dann verzweigt sich das System entsprechend der Eigenzustände von A (man betrachte z.B. ein Spin-Singulett; dieses kann ich bzgl. jeder beliebigen Achse definieren, aber die Festlegung, dass ich die z-Komponente messe, führt zu einer Verzweigung entsprechend der z-Komponente, nicht bzgl. einer anderen wie z.B. der x-Komponente)
3) wird ebenfalls gelöst von der Dekohärenz
4) muss gelöst werden mittels weiterer Argumente (und ggf. zusätzlicher Annahmen), aus denen das Auftreten von Wahrscheinlichkeiten in natürlicher Weise folgt; dazu gibt es eine Reihe unterschiedlicher Ansätze; ich denke, man ist sich heute weitgehend einig, dass keiner wirklich allgemein akzeptiert und "natürlich" ist. |
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 02. Sep 2015 13:07 Titel: TomS Verfasst am: 02. Sep 2015 13:07 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Genau diese Frage stelle ich in Bezug auf die MWI: Wie darf ich mir vorstellen, daß eine einzelne Katze eine Superposition von Zweigen ist? |
Ich kann mir das nicht vorstellen. Ich kann mir aber auch keine Superposition eines Elektrons mit zwei Komponenten entsprechend zwei Aufenthaltsmaxima hier und auf dem Mond vorstellen. „Vorstellen“ im Rahmen der QM bedeutet im Wesentlichen, Gleichungen zu verstehen.
| index_razor hat Folgendes geschrieben: | | Welche spezifischen, insbesondere quantitativen Aussagen macht denn die MWI über einzelne Systeme? |
Die selbe wie viele andere Interpretationen auch.
Welche erwartest du denn?
| index_razor hat Folgendes geschrieben: | | … außer dem Glaubenssatz, daß sich dieses einzelne System wahrhaftig in dem Zustand befindet, den es laut QM-Formalismus haben sollte … |
Ja, das ist der Kern.
Was erwartest du mehr?
| index_razor hat Folgendes geschrieben: | | Zitat: | Meiner Meinung nach ist der Begriff "Many Worlds" ungünstig, denn der Begriff Worlds ist etwas schwammig. Ich sehe das so: Akzeptiert man den Zustand als das was real existiert, dann ist die real existierende Welt ein einziger Zustand, welcher eine Superposition aus den möglichen von einem in diesem Zustand lebenden Beobachter wahrgenommenen Zuständen ist.
Insofern ist die E.I sehr einfach, sie behauptet nicht der Zustand sei eine Beschreibung, sie gesteht ihm reale Existenz zu. |
Die Welt ist ein Zustand? |
Ich verstehe bassiks so, dass er meint, die Welt entspricht exakt einem Zustand.
| index_razor hat Folgendes geschrieben: | | Mir ist nun nicht so klar, wie ihr euch vorstellt, daß die MWI diese Problem gelöst haben soll. Aussagen wie "das System ist der Zustand" ergeben keinen Sinn oder sind völlig trivial. |
Vergiss das ist und ersetze es durch entspricht.
Ja, die Aussagen sind trivial, und gerade deswegen so genial.
| index_razor hat Folgendes geschrieben: | | Dann bleibt: "Das System ist das, was der Zustand beschreibt." Das ist trivial. |
Wenn es so trivial wäre wieso kannst du es dann nicht einfach akzeptieren? Was stört dich daran? Oder was ist (trivialerweise) falsch?
| index_razor hat Folgendes geschrieben: | | Zitat: | | Gesteht man dem Zustand nämlich reale Existenz zu, so ist die Theorie vollkommen deterministisch. |
Das deterministische ist die Schrödingergleichung. Deren Determinismus ist noch völlig unabhängig von der Interpretation. |
Ja, der Determinismus der Schrödingergleichung ist unabhängig von der Interpretation.
Die Everett-I. behauptet jedoch, dass sich auch die reale Welt absolut deterministisch verhält (und dass man aus dem Formalismus heraus zeigen kann, weshalb trotzdem stochastisches Verhalten beobachtet wird)
| index_razor hat Folgendes geschrieben: | | Also ist Dekohärenz irrelevant, wenn es um den Vergleich verschiedener Interpretationen geht. |
Nein.
Die Everett-I. ohne Dekohärenz ist sicher in einer vergleichsweise unbequemen Situation. Die Wahrnehmung der Everett-I. hat sich historisch jedoch gerade wegen der Dekohärenz gewandelt, weil diese einige Teillösungen anbieten, die Everett noch postulieren musste.
Insbs. der orthodoxen / Kopenhagen- / Kollaps-I. hilft die Dekohärenz dagegen gar nichts.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 02. Sep 2015 13:17 Titel: TomS Verfasst am: 02. Sep 2015 13:17 Titel: |
 |
|
Ich hätte den Vorschlag, dass wir kurz unterbrechen und diskutieren, wie wir weiter machen. Die Beiträge werden immer länger und unübersichtlicher; wesentliche Argumente gehen evtl. zwischen eher sekundären Bemerkungen verloren; die Diskussion der Ensemble-I. ist noch zu früh; ...
Mein Vorschlag wäre, dass wir zunächst nur die Everett-I. diskutieren und andere I. außen vorlassen. Ich würde dann einige zentrale Merkmale zusammenfassen (zwei Axiome, deterministisch, "naive Ontologie") die sich in der bisherigen Diskussion herauskristallisiert haben. Insbs. index_razor kann seine zentralen Einwände formulieren ("naive Ontologie, ggf. weitere).
Haltet ihr das für sinnvoll?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 02. Sep 2015 13:26 Titel: bassiks Verfasst am: 02. Sep 2015 13:26 Titel: |
 |
|
|
Klingt nach einem vernünftigen Plan. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Sep 2015 13:38 Titel: index_razor Verfasst am: 02. Sep 2015 13:38 Titel: |
 |
|
|
Das können wir gern machen nachdem ich ein paar Punkte aus deinen letzten Antworten an mich klargestellt oder zumindest kommentiert habe. Ich bin allerdings im Augenblick etwas pessimistisch, ob wir noch mehr erreichen werden als Wiederholungen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Sep 2015 14:07 Titel: index_razor Verfasst am: 02. Sep 2015 14:07 Titel: |
 |
|
Ich bin der Ansicht, daß deine letzten Antworten einfach die wesentlichen Argumente gegen die MWI ignorieren. Insofern glaube ich nicht, daß wir hier noch viele Fortschritte machen werden. Aber ich habe nichts gegen einen Versuch.
Folgendes wollte ich vorher noch kurz versuchen klarzustellen.
| TomS hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: | | Die Frage ob ich die Wahrscheinlichkeiten in der Theorie postulieren muß oder ableiten kann, ist eine rein logische und hat mit der Interpretation nicht das geringste zu tun. Ich kann einfach alle logischen Beziehungen zwischen allen wahren Aussagen der QM ignorieren, sie alle wie Postulate behandeln und habe exakt gar nichts am Interpretationsproblem geändert. Es existiert genau wie vorher. |
Verstehe ich nicht. Seit wann haben Logik und Interpretation nichts miteinander zu tun?
|
Die logischen Beziehungen zwischen Aussagen, wie Ableitbarkeit oder Widersprüchlichkeit, kann ich (zumindest prinzipiell) mit Hilfe formaler Beweise klären, völlig unabhängig von Interpretationen.
| Zitat: | | Wenn du mit einer realen, objektiven, deterministischen und vollständigen Interpretation startest, dann kannst du Wahrscheinlichkeiten gar nicht zusätzlich einführen, da dies den Voraussetzungen explizit widersprechen würde. Du musst also entweder das Auftreten von Wahrscheinlichkeiten aus den Annahmen heraus ableiten bzw. motivieren, oder du musst bestimmte Annahmen aufgeben |
Dieses Argument kam in ähnlicher Form immer wieder und ich finde es ehrlich gesagt völlig konfus. Wenn eine Aussage, in der Wahrscheinlichkeiten auftreten, meinen Voraussetzungen explizit widerspricht, dann kann ich sie unmöglich aus meinen gemachten Annahmen ableiten, es sei denn diese sind schon widersprüchlich. Es gäbe einfach keine Möglichkeit diese Wahrscheinlichkeitsaussagen in die Theorie einzufügen ohne eine Inkonsistenz zu erzeugen. Und wenn ich sie ableiten kann, dann kann ich sie unter logischen Gesichtspunkten genauso gut als Axiom einführen. Das ist dann zwar nicht unabhängig, das ist den Interpretationen aber egal.
| Zitat: | | index_razor hat Folgendes geschrieben: | | Die MWI hat genau mit dieser eindeutigen Spezifikation Probleme. Sie behauptet zwar einfach ein Zustand beschreibe viele Welten, kann aber außerhalb gewisser Näherungen nicht eindeutig sagen, in welchem Zustand sich diese Welten befinden. |
Falsch!
Sie behauptet, dass genau eine Welt mit einer Zweigstruktur existiert. Und diese Zweigstruktur ist eben gerade so gut berechenbar, wie die Gleichungen im Kontext der Dekohärenz lösbar sind (es ist heute sinnlos, ohne die Dekohärenz zu argumentieren).
|
Dekohärenz ist ja genau, was ich mit "gewissen Näherungen" meine. Also ist die Aussage richtig.
Das Problem mit deiner Aussage ist: Die Zweigstruktur ist i.A. nicht eindeutig angebbar.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Generell ist das Thema, ob eine Aussage der Theorie ein Axiom oder ein Theorem ist, von völlig untergeordneter Bedeutung. Eine Frage der Interpretation ist, was die Theorie, also die Gesamtheit ihrer Aussagen, bedeutet, nicht, welche ihrer Aussagen ich aus welchen ableiten kann. |
Dann arbeiten also alle Vertreter der Everett-I., die sich diesem Thema widmen, sowie alle Kritiker, die genau diese Arbeiten hinterfragen, an einem Scheinproblem. Sorry, aber deine Aussage ist absolut nicht ernst zu nehmen.
|
Nicht ernstzunehmen ist höchstens diese Deutung meiner Aussage. Ich habe nicht von Scheinproblem gesprochen, sondern von einem Problem von untergeordneter Bedeutung. Und zwar im Kontext des Vergleichs "Ableitbarkeit einer Aussage aus Postulaten" und "Bedeutung dieser Aussage". Ob eine Aussage aus anderen ableitbar ist, ist natürlich kein Scheinproblem, sondern eine Frage der Mächtigkeit meiner Axiome. Die Bedeutung einer Aussage ist in unserem Zusammenhang aber primär, eine Frage der Interpretation, und hat nichts damit zu tun woraus ich sie ableiten kann.
| Zitat: | Kannst du mal in eigenen Worten zusammenfassen, worin deiner Meinung nach das Messproblem besteht? Dann kann ich evtl. versuchen, zu erklären, inwiefern die Everett-I. (auf Basis der Dekohärenz) dieses Problem tatsächlich löst.
|
Das habe ich, denke ich, schon mehrfach getan. An dieser Stelle genügt glaube ich, daß m.E. die Dekohärenz das Meßproblem höchstens zum Teil löst (im engeren Sinne von "Messen", als WW mit Systemen von vielen Freiheitsgraden), und daß deswegen die Aussagen der QM über mikrsokopische isolierte System unklar bleiben, wenn sie auch aus phänomenologischer Sicht eher Randfälle sind.
| Zitat: | | index_razor hat Folgendes geschrieben: | | Mehrere Zweige liegen "in der Praxis" auch nicht vor, sondern nur immer einer. |
Was meinst du mit „in der Praxis“?
|
Ich gehe davon aus, dasselbe wie du gemeint zu haben.
| Zitat: |
Der wesentliche offene Punkte ist die Frage nach dem Auftreten von Wahrscheinlichkeiten (siehe Carroll, Wallace, Saunders, …). Aber das ist nicht dein wesentliches Problem mit dieser Interpretation; du hast offensichtlich schon früher prinzipielle Vorbehalte (s.o.)
|
Ja, genau so ist es.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Everett, Rev.Mod.Phys. 29 (1957). Darin ist natürlich von Dekohärenz nicht die Rede. Er wendet die Viele-Welten-Interpretation ausdrücklich auf geschlossenen Systeme in reinen Zuständen an, nicht auf Gemische. |
Das halte ich für unbefriedigend und inzwischen überholt.
|
"Unbefriedigend" ist in diesem Zusammenhang seltsam. Everett hat versucht das Problem ganz allgemein zu lösen. Hätte er Erfolg gehabt, wäre seine Lösung ohne weiteres auch auf Situationen anwendbar, in denen Dekohärenz auftritt. Das einzig unbefriedigende ist, daß diese Lösung nicht allgemein funktioniert. Die Abschwächung des Ausgangsproblems, so daß es zur Lösung paßt, die man schon kennt, kann man doch nicht als befriedigender ansehen.
Zuletzt bearbeitet von index_razor am 02. Sep 2015 14:52, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Sep 2015 14:41 Titel: index_razor Verfasst am: 02. Sep 2015 14:41 Titel: |
 |
|
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Welche spezifischen, insbesondere quantitativen Aussagen macht denn die MWI über einzelne Systeme? |
Die selbe wie viele andere Interpretationen auch.
Welche erwartest du denn?
|
Keine weiteren. Daß die Situation in der Ensembleinterpretation nicht schlechter ist, wollte ich nur klarstellen. Denn bassiks Bemerkung klang so, als sähe er darin einen Nachteil der Ensembleinterpretation.
| Zitat: | | index_razor hat Folgendes geschrieben: | | Dann bleibt: "Das System ist das, was der Zustand beschreibt." Das ist trivial. |
Wenn es so trivial wäre wieso kannst du es dann nicht einfach akzeptieren? |
Deshalb:
| index_razor hat Folgendes geschrieben: |
Stell dir vor, du erhältst einen Brief mit dem Inhalt "asla lksazwuwu laksjdlas lakskdsla" und fragst dich was das bedeuten soll. Jemand sagt dir, er habe dieses Problem für dich gelöst: Seiner festen philosophischen Überzeugung nach ist die Aussage in der Nachricht wahr. Und sie drückt genau den Sachverhalt aus, daß eben asla lksazwuwu laksjdlas lakskdsla. Fühlst du dich jetzt schlauer oder ernst genommen? Wenn du jetzt sagst, daß dir das keinen Deut weiterhilft und daß man ja normalerweise die Bedeutung einer Aussage nicht aus ihrem vorausgesetzten Wahrheitsgehalt erschließt, sondern umgekehrt, wird erwidert: "Ja, ja, aber es ist eben meine philosophische Überzeugung, daß Nachrichten eine Bedeutung haben sollten und nicht einfach nur Kauderwelsch enthalten. Aber wenn du diese Überzeugung nicht teilst, bist du ja vielleicht der Meinung, daß man sich auch nur auf das Lesen der Zeichenketten beschränken kann, und man den Inhalt gar nicht so genau verstehen müsse. Dann hast du eben einfach geringere Ansprüche an den Inhalt von Nachrichten..." Das ist so in etwa die Situation in der Interpetationsdiskussion. ;-)
|
Deine Interpretation der QM, "Es existiert genau das, was der Zustand beschreibt. Dem System entspricht ein Zustandsvektor." ist analog zur Interpretation des Briefes. Dein Einwand, daß man ja die klassischen Mechanik genauso interpretiert, ist ja durchaus berechtigt. Der Unterschied ist: diese Interpretation liefert in der klassischen Mechanik eine vollständige, realistische Erklärung aller Phänomene. In der QM tut sie das nicht.
Es gibt in der klassischen Mechanik weit weniger Anlaß zum Zweifeln, daß die Beschreibung des Systems mittels Phasenraumpunkt irgendwelche Fragen unbeantwortet läßt, die man sinnvollerweise an das System stellen kann. Insbesondere kann ich ja jedes mögliche Phänomen eindeutig vorhersagen: Jeder mögliche Meßwert ist eine eindeutige Funktion des Zustands. Warum ist meine QM-Beschreibung im Vergleich dazu so unspezifisch? Wenn der Zustandsvektor eindeutig dem System entspricht, ist dann die Realität unspezifisch? Die Ergebnisse von Messungen sind es nicht. Also entsprechen den Meßergebnissen keine Elemente der Realität? Das sind so ungefähr die wesentlichen Interpretationsfragen, die ich für offen halte und die m.E. keine Interpretation plausibel beantworten kann. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 02. Sep 2015 15:08 Titel: bassiks Verfasst am: 02. Sep 2015 15:08 Titel: |
 |
|
| Zitat: | | Wenn eine Aussage, in der Wahrscheinlichkeiten auftreten, meinen Voraussetzungen explizit widerspricht, dann kann ich sie unmöglich aus meinen gemachten Annahmen ableiten, es sei denn diese sind schon widersprüchlich. |
Ich denke hier hast du etwas falsch verstanden (oder ich?). Die E.I ist deterministisch. Was man aus der E.I ableiten will ist eine Erklärung warum wir Wahrscheinlichkeiten wahrnehmen. Die Wahrscheinlichkeiten sind also keine fundamentale Eigenschaftl der Theorie mehr, sondern lediglich was ein Beobachter wahrnimmt. (anders als in anderen Interpretationen, in welchen die Wahrscheinlichkeiten aus Unkenntnis resultieren oder gar als fundamentale Eigenschaft der Natur postuliert werden). |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Sep 2015 15:19 Titel: index_razor Verfasst am: 02. Sep 2015 15:19 Titel: |
 |
|
| bassiks hat Folgendes geschrieben: | | Zitat: | | Wenn eine Aussage, in der Wahrscheinlichkeiten auftreten, meinen Voraussetzungen explizit widerspricht, dann kann ich sie unmöglich aus meinen gemachten Annahmen ableiten, es sei denn diese sind schon widersprüchlich. |
Ich denke hier hast du etwas falsch verstanden (oder ich?). Die E.I ist deterministisch. Was man aus der E.I ableiten will ist eine Erklärung warum wir Wahrscheinlichkeiten wahrnehmen. Die Wahrscheinlichkeiten sind also keine fundamentale Eigenschaftl der Theorie mehr, sondern lediglich was ein Beobachter wahrnimmt. (anders als in anderen Interpretationen, in welchen die Wahrscheinlichkeiten aus Unkenntnis resultieren oder gar als fundamentale Eigenschaft der Natur postuliert werden). |
Und was habe ich nun falsch verstanden?
Ich schlage übrigens vor für die MWI nicht die Abkürzung E.I. zu verwenden, denn die einzige hier wesentlich mitdiskutierte Alternative hat dieselben Initialen. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 02. Sep 2015 15:31 Titel: bassiks Verfasst am: 02. Sep 2015 15:31 Titel: |
 |
|
| Zitat: | | Wenn eine Aussage, in der Wahrscheinlichkeiten auftreten, meinen Voraussetzungen explizit widerspricht, dann kann ich sie unmöglich aus meinen gemachten Annahmen ableiten, es sei denn diese sind schon widersprüchlich. |
Dieser logische Widerspruch macht für mich nur dann Sinn, wenn du als Voraussetzung Determinismus annimmst, und dann aber ableiten willst, dass deine Theorie nicht deterministisch ist (Wahrscheinlichkeiten...). Genau das wird aber nicht gemacht, die Theorie bleibt deterministisch, es soll nur abgeleitet werden, warum wir statistische Häufigkeiten wahrnehmen.
Sollte ich dich falsch verstanden haben, bitte ich dich, diesen Widerspruch etwas genauer auszuführen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Sep 2015 15:40 Titel: index_razor Verfasst am: 02. Sep 2015 15:40 Titel: |
 |
|
| bassiks hat Folgendes geschrieben: |
Sollte ich dich falsch verstanden haben, bitte ich dich, diesen Widerspruch etwas genauer auszuführen. |
Ich behaupte doch gar keinen Widerspruch, sondern TomS:
| TomS hat Folgendes geschrieben: |
Wenn du mit einer realen, objektiven, deterministischen und vollständigen Interpretation startest, dann kannst du Wahrscheinlichkeiten gar nicht zusätzlich einführen, da dies den Voraussetzungen explizit widersprechen würde.
|
Ich sage nur, wenn es da irgendeinen Widerspruch zwischen den deterministischen und den probabilistischen Aussagen der Theorie gäbe, wäre es hoffnungslos letztere aus ersteren abzuleiten. Da es keinen Widerspruch gibt, kann ich sie aber für Fragen der Interpretation beide als Postulate behandeln. TomS sieht das sicher irgendwie anders, ich kann mir aber keinen Reim darauf machen, wie er das sieht. |
|
 |
|
|
















 Die transaktionale Interpretation war für mich auch ganz interessant, für die ich auch einen Thread erstellt habe, aber leider weiß keiner dazu bescheid. So oder so, ich habe so einbisschen meine Probleme damit.
Die transaktionale Interpretation war für mich auch ganz interessant, für die ich auch einen Thread erstellt habe, aber leider weiß keiner dazu bescheid. So oder so, ich habe so einbisschen meine Probleme damit.

 ) du bist.
) du bist.