| Autor |
Nachricht |
WhiteRussian

Anmeldungsdatum: 16.05.2011
Beiträge: 56
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 24. Mai 2011 12:59 Titel: TomS Verfasst am: 24. Mai 2011 12:59 Titel: |
 |
|
Es gibt mehrere Möglichkeiten dafür.
Zum ersten ist die potentielle Energie immer über die Höhe definiert, unabhängig davon, ob das Teilchen nun auf dem Kegel sitzen muss oder nicht.
Um das Teilchen auf den Kegel zu setzen, kannst du zwei Vorgehensweisen wählen
1) du nutzt eine Parameterdarstellung des Kegels und die darin enthaltenen zwei Koordinaten als verallgemeinerte Koordinaten, durch die du die Geschwindigkeiten ausdrückst und die Lagrangefunktion bestimmst
2) du lässt das Teilchen zunächst in drei Dimensionen leben und zwingst es durch die Einführung einer Zwangsbedingung mit Lagrangemultiplikator auf den Kegel
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
WhiteRussian

Anmeldungsdatum: 16.05.2011
Beiträge: 56
|
 WhiteRussian Verfasst am: 24. Mai 2011 13:37 Titel: WhiteRussian Verfasst am: 24. Mai 2011 13:37 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Es gibt mehrere Möglichkeiten dafür.
Zum ersten ist die potentielle Energie immer über die Höhe definiert, unabhängig davon, ob das Teilchen nun auf dem Kegel sitzen muss oder nicht.
|
Das Teilchen muss auf der Kegelwand sitzen. Die Frage ist, ob es dabei Kreisbewegungen machen kann.
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 24. Mai 2011 13:48 Titel: Keplerfan Verfasst am: 24. Mai 2011 13:48 Titel: |
 |
|
Ja, kann es! 
Es kommt dabei auf die Anfangsbedingung an. Wenn du dir einen Roulettetisch vorstellst, in den der Angestellte des Casinos die Kugel wirft, wird die Sache vielleicht klarer. Dieses "Kreisen" funktioniert auch, wenn das Roulette selbst sich dabei nicht dreht.
Zur Illustration:
http://www.youtube.com/watch?v=fnRo2REqPnY
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 24. Mai 2011 15:14 Titel: TomS Verfasst am: 24. Mai 2011 15:14 Titel: |
 |
|
| WhiteRussian hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Es gibt mehrere Möglichkeiten dafür.
Zum ersten ist die potentielle Energie immer über die Höhe definiert, unabhängig davon, ob das Teilchen nun auf dem Kegel sitzen muss oder nicht.
|
Das Teilchen muss auf der Kegelwand sitzen.. |
Das ist schon klar. Ich wollte auf folgendes hinaus: du kannst die Lagrangefunktion in physikalischen Koordinaten aufstellen (siehe mein 1) oder zunächst in unphysikalischne Koordinaten (siehe mein 2). In beiden Fällen ist die potentielle Energie immer mgh, wobei h eben von den jeweiligen Koordinaten abhängt. Die Methode, wie du das Teilchen auf den Kegel zwingst, kannst du dir aussuchen; 1) und 2) liefern beide das richtige Ergebnis.
Warum schreibst du nicht einfach mal deine Darstellung für den Kegel, d.h. die Koordinaten, sowie die daraus resultierende Lagrangefunktion (oder Lagrangefunktionen für 1 und 2) hin?
| WhiteRussian hat Folgendes geschrieben: | | Die Frage ist, ob es dabei Kreisbewegungen machen kann |
Dazu musst du die Bewegungsgleichungen aufstellen und lösen. Du wirst u.U. als Lösung einen Kegelschnitt finden (auch das ist sicher nicht der allgemeinste Fall), ein Kreis wäre dabei ein Spezialfall. Ich bezweifle jedoch (aus physikalischen Gründen), dass unter Berücksichtugung der Schwerkraft ein Kreis (bei konstanter Höhe h) eine zulässige Lösung ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 24. Mai 2011 15:22 Titel: Keplerfan Verfasst am: 24. Mai 2011 15:22 Titel: |
 |
|
| Zitat: |
Dazu musst du die Bewegungsgleichungen aufstellen und lösen. Du wirst u.U. als Lösung einen Kegelschnitt finden (auch das ist sicher nicht der allgemeinste Fall), ein Kreis wäre dabei ein Spezialfall. Ich bezweifle jedoch (aus physikalischen Gründen), dass unter Berücksichtugung der Schwerkraft ein Kreis (bei konstanter Höhe h) eine zulässige Lösung ist. |
Meiner Meinung nach müsste ein Kreis eine zulässige Lösung sein. Man bekommt sie, wenn man die radiale Anfangsgeschwindigkeit null setzt und die anfängliche Winkelgeschwindigkeit so wählt, dass die Zentrifugalkraft die Schwerkraft gerade kompensiert.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 24. Mai 2011 15:42 Titel: TomS Verfasst am: 24. Mai 2011 15:42 Titel: |
 |
|
OK, ja, könnte gehen. Aber warum schreibst du nicht die Bewegungsgleichunegn auf und überprüfst diesen Spezialfall?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
WhiteRussian

Anmeldungsdatum: 16.05.2011
Beiträge: 56
|
 WhiteRussian Verfasst am: 25. Mai 2011 11:04 Titel: WhiteRussian Verfasst am: 25. Mai 2011 11:04 Titel: |
 |
|
Gelobt sei das Repetitorium der höheren Mathematik  Dort habe ich folgende Parametrisierung des Kegels gefunden: Dort habe ich folgende Parametrisierung des Kegels gefunden:

H ist die Maximalhöhe, R der maximalumfang. Das ganze ist nach oben geöffnet. Scheint doch zu passen, oder?
Doch wie stelle ich nun die Lagrangefunktion auf? Theta, Alpha und r sind wohl die verallgemeinerten Koordinaten? Wobei das Alpha ja konstant ist, d.h. r und Theta würden wohl ausreichen. [/latex]
Zuletzt bearbeitet von WhiteRussian am 25. Mai 2011 11:14, insgesamt einmal bearbeitet |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 25. Mai 2011 11:14 Titel: Keplerfan Verfasst am: 25. Mai 2011 11:14 Titel: |
 |
|
Ja ... da steckt aber kein Geheimnis dahinter: Die ersten beiden Koordinaten sind normale Polarkoordinaten und die letzte die Beziehung  . . 
Zwei Koordinaten ist richtig. Du hast ja drei Dimensionen minus eine Zwangsbedingung, also bleiben 2 Koordinaten übrig.
Zuletzt bearbeitet von Keplerfan am 25. Mai 2011 11:18, insgesamt einmal bearbeitet |
|
 |
WhiteRussian

Anmeldungsdatum: 16.05.2011
Beiträge: 56
|
 WhiteRussian Verfasst am: 25. Mai 2011 11:17 Titel: WhiteRussian Verfasst am: 25. Mai 2011 11:17 Titel: |
 |
|
Ich bin noch sehr ungeübt mit den Lagrange-Funktionen (deswegen spamme ich hier auch soviel rum).
Also ich versuchs mal


Nur wie setze ich jetzt hier die Parametrisierung richtig ein?
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 25. Mai 2011 11:24 Titel: Keplerfan Verfasst am: 25. Mai 2011 11:24 Titel: |
 |
|
| WhiteRussian hat Folgendes geschrieben: | Ich bin noch sehr ungeübt mit den Lagrange-Funktionen (deswegen spamme ich hier auch soviel rum).
Also ich versuchs mal


Nur wie setze ich jetzt hier die Parametrisierung richtig ein? |
Ich nehme an, du meinst 
h ist ja das gleiche wie z.
Du musst zunächst die zeitlichen Ableitungen bilden, indem du deine Parametrisierung differenzierst:

In der pot. Energie kannst du einfach das z einsetzen, das schon in der Parametrisierung steht.
|
|
 |
WhiteRussian

Anmeldungsdatum: 16.05.2011
Beiträge: 56
|
 WhiteRussian Verfasst am: 25. Mai 2011 11:48 Titel: WhiteRussian Verfasst am: 25. Mai 2011 11:48 Titel: |
 |
|
 - r\dot \theta \cdot sin(\theta) \\ \dot r sin(\theta) + r\dot \theta \cdot cos(\theta) \\ \dot r cot(\theta) - (r\dot \theta) / (sin^2(\theta)\end{pmatrix} )
Womit wir dann die Lagrangefunktion
) hätten. hätten.
Sieht gut aus, oder?
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 25. Mai 2011 12:01 Titel: Keplerfan Verfasst am: 25. Mai 2011 12:01 Titel: |
 |
|
Ja, und nun bitte ausrechnen.  
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 25. Mai 2011 12:07 Titel: franz Verfasst am: 25. Mai 2011 12:07 Titel: |
 |
|
|
Mein Hinweis, wie immer: LANDAU / LIFSCHITZ, I § 14 Aufgabe 2 ... kubische Gleichung in r; übrigens mit zwei positiven Lösungen, welche die horizontalen Extremalkreise sind, zwischen denen sich der Punkt bewegen kann.
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 25. Mai 2011 14:50 Titel: Keplerfan Verfasst am: 25. Mai 2011 14:50 Titel: |
 |
|
Moment ... deine letzte Komponente stimmt nicht. Da steckt kein 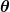 drin. drin.
Ich erhalte für die kinetische Energie den Ausdruck
 \dot r^2 + r^2 \dot \theta^2\right))
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 25. Mai 2011 15:46 Titel: Keplerfan Verfasst am: 25. Mai 2011 15:46 Titel: |
 |
|
Meine Lagrangegleichungen sind (Korrektur:)
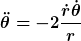
 )
Zuletzt bearbeitet von Keplerfan am 25. Mai 2011 16:26, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 25. Mai 2011 15:55 Titel: TomS Verfasst am: 25. Mai 2011 15:55 Titel: |
 |
|
Man hat natürlich die Wahl, welche Koordinaten man nutzt; ich hätte jetzt nicht r sondern direkt z, also h als Koordnate verwendet
 \\ r\,\sin(\theta) \\ z \end{pmatrix} = \begin{pmatrix} z\,\tan(\alpha)\,\cos(\theta) \\ z\,\tan(\alpha)\sin(\theta) \\ z \end{pmatrix} )
\,\cos(\theta) \\ \dot{z}\,\tan(\alpha)\sin(\theta) \\ \dot{z} \end{pmatrix} + \begin{pmatrix} -z\dot{\theta}\,\tan(\alpha)\,\sin(\theta) \\ z\dot{\theta}\,\tan(\alpha)\cos(\theta) \\ 0 \end{pmatrix} )
und damit fürL = T - V
+1) + z^2\,\dot{\theta}^2\,\tan^2(\alpha)\right])

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 25. Mai 2011 15:56 Titel: franz Verfasst am: 25. Mai 2011 15:56 Titel: |
 |
|
|
Das erste ist doch der Drehimpulssatz (zyklische Variable)?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 25. Mai 2011 16:09 Titel: TomS Verfasst am: 25. Mai 2011 16:09 Titel: |
 |
|
M.E. ist der Weg über die Lagrange-Gleichungen zu kompliziert.
Besser ist es, die Erhaltungsgrößen (Stichwort: zyklische Koordinaten) zu bestimmen.
Konkret:
- konjugierter Impuls zum Winkel theta: entspricht Drehimpuls L und ist erhalten, da theta zyklisch ist
- konjugierter Impuls zu r (bzw. bei mir: z); ist nicht erhalten, da r nicht zyklisch
Energie E = T + V ist natürlich ebenfalls erhalten. Daraus folgt eine DGL erster Ordnung durhc Trennung der Variablen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 25. Mai 2011 16:14 Titel: TomS Verfasst am: 25. Mai 2011 16:14 Titel: |
 |
|
Deine Gleichungen stimmen m.E. nicht.
Wenn du die Gleichung für theta betrachtest, dann bekommst du ja

theta ist zyklisch.
Dann leitest du ab:

Die Zeitableitung angewandt auf diesen Term wirkt aber sowohl auf theta als auch auf r, d.h. dass eben nicht

sondern

OK?
Die Gleichung fürr musst du daraufhin ebenfalls nochmal prüfen.
Aber wie gesagt, ich denke, du kommst mittels des Einsetzens des erhaltenen Drehimpulses L in die erhaltene Energie E zu einer DGL. erster Ordnung - und das ist wesentlich leichter.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 25. Mai 2011 16:24 Titel: Keplerfan Verfasst am: 25. Mai 2011 16:24 Titel: |
 |
|
Stimmt, hoffe ich habs jetzt korrigiert. Kam mir auch komisch vor, da der Drehimpuls ja erhalten sein sollte. Die Gleichung für r sollte richtig sein, da nach der Ableitung nach  kein kein 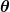 mehr übrig bleibt. Danke. mehr übrig bleibt. Danke. 
Deine Anmerkungen zu den Erhaltungsgrößen sind sehr hilfreich!
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 25. Mai 2011 17:06 Titel: TomS Verfasst am: 25. Mai 2011 17:06 Titel: |
 |
|
Jetzt wärst du soweit, um zu diskutieren ob eine Kreisbahn mit r=const. als Lösung zulässig ist ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
WhiteRussian

Anmeldungsdatum: 16.05.2011
Beiträge: 56
|
 WhiteRussian Verfasst am: 25. Mai 2011 17:17 Titel: WhiteRussian Verfasst am: 25. Mai 2011 17:17 Titel: |
 |
|
Kommt ihr auch aus Freiburg oder macht ihr das nur zum Spaß 
Dass die letzte Komponente falsch war habe ich gesehen. Das muss natürlich ein Alpha sein.
Jetzt sollen wir aus dieser Funktion die Lagrangegleichung gewinnen. Ich habe leider nicht so ganz den Plan wie das geht, da ich das mit den verallgemeinerten Koordinaten nicht so ganz verstehe.
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 25. Mai 2011 21:49 Titel: Keplerfan Verfasst am: 25. Mai 2011 21:49 Titel: |
 |
|
Du kannst dir das mit den Lagrange-Gleichungen so ähnlich vorstellen wie mit der Gesamtenergie. Aus der Gesamtenergie eines Teilchens in einer Dimension kann man ja auch die Bewegungsgleichungen des Teilchens gewinnen, nämlich gemäß:
)
Die Bewegungsgleichungen folgen nun gemäß
^\cdot = -\frac{\partial }{\partial x} E_{ges} )
Wenn du diese Gleichungen mit den Lagrange-Gleichungen
 ^\cdot=\frac{\partial L}{\partial {q}} )
vergleichst, sehen sie diesen schon recht ähnlich. Wenn man die Energie oben in die Energie-Gleichung einsetzt, ergibt sich:

Es lässt sich also tatsächlich die Bewegungsgleichung aus der Energie herleiten. Der einzige Unterschied bei den Lagrange-Gleichungen zu der Gleichung oben ist nun, dass das Vorzeichen vor der Ableitung nach x vertauscht ist. Das liegt einfach darin, dass ja für die Energie gilt

Für die Lagrangefunktion hingegen

Sie hat das Minus beim Potential also sozusagen schon eingebaut.
Bei der Berechnung einer analytischen Lösung der entstehenden Gleichungen (auch aus der DGL 1. Ordnung aus der Energie) bin ich bislang gescheitert, werd es vielleicht in ein paar Tagen noch einmal versuchen. Die Kreisbahn müsste sich bei meinen Lagrange-Gleichungen rel. leicht beweisen lassen, wenn man die anfängliche radiale Geschwindigkeit auf 0 setzt und die anfängliche Winkelgeschwindigkeit so wählt, dass sich Schwerkraft und Fliehkraft in der Gleichung für r aufheben. Dann gibt es keine Beschleunigung irgendeiner Koordinate, und die Kreisbahn ist stabil. 
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 25. Mai 2011 22:22 Titel: TomS Verfasst am: 25. Mai 2011 22:22 Titel: |
 |
|
Die hier beschriebene Vorgehensweise entspricht dem kanonischen Formalismus, in dem die Bewegungsgleichungen in x und p ausgehend von der Hamiltonfunktion H (die im wesentlichen der Energie E entspricht) hergeleitet werden
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 26. Mai 2011 00:49 Titel: franz Verfasst am: 26. Mai 2011 00:49 Titel: |
 |
|

+mgr cot\alpha)


Die Energiegleichung kann gelesen werden als eindimensionale Bewegung eines Massepunktes im Ersatzpotential U_eff(r). An einer vollständigen Lösung bestehen Zweifel.
Zuletzt bearbeitet von franz am 26. Mai 2011 13:28, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 26. Mai 2011 01:37 Titel: TomS Verfasst am: 26. Mai 2011 01:37 Titel: |
 |
|
Idee: damit könnte man durch Reskalierung von m und g das Problem in ein einfacheres überführen; die Energie und damit auch die Lagrangefunktion wären dann äquivalent zu der eines Teilchen neuer Masse m' mit neuer Konstante g' auf einer Ebene mit linear ansteigendem Potential.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 26. Mai 2011 09:59 Titel: Keplerfan Verfasst am: 26. Mai 2011 09:59 Titel: |
 |
|
|
Kannst du kurz erläutern, was mit "Reskalierung" gemeint ist und wie das konkret aussehen würde?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 26. Mai 2011 13:58 Titel: TomS Verfasst am: 26. Mai 2011 13:58 Titel: |
 |
|
Ich gehe aus von


Jetzt führe ich ein


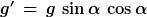
Dann erhalte ich eine neue Darstellung der Energie

Dies ist die Energie E eines Teilchens der Masse m' mit Drehimpuls J' in einem linearen Potential; d.h. der Effekt des Kegels wird durch die Reskalierung der Konstanten in diese absorbiert und man hat ein ganz normales Teilchen (in einem linearen Potential) in der Ebene (natürlich ist die Reskalierung singulär für bestimmte Öffnungswinkel des Kegels).
Jetzt betrachte ich noch den Drehimpuls J'

Nun könnte man statt r(t) wie üblich für die Parameterdarstellung r(\theta) berechnen, indem man Trennung der Variablen anwendet und formal dt mittels d\theta eliminiert. Ich denke aber nicht, dass das geschlossen lösbar ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 26. Mai 2011 19:49 Titel: Keplerfan Verfasst am: 26. Mai 2011 19:49 Titel: |
 |
|
Ich habe zum Spaß mal versucht, das hinzubekommen - leider ohne Erfolg. Allein der kräftefreie Fall (g'=0) gestaltet sich in Polarkoordinaten schon wesentlich schwieriger als in kartesischen Koordinaten und ergibt eine komplizierte Abhängigkeit der Form
 = \sqrt{(\pm a\cdot t +b)^2+c}.)
Das jetzt noch mit zusätzlicher Kraft - Puh. 
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 26. Mai 2011 20:15 Titel: TomS Verfasst am: 26. Mai 2011 20:15 Titel: |
 |
|
Du könntest versuchen, den Fall r(t) = const. zu lösen - oder zu beweisen, dass es keine Lösung gibt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 26. Mai 2011 21:01 Titel: Keplerfan Verfasst am: 26. Mai 2011 21:01 Titel: |
 |
|





Kreise mit diesem Radius sollten also stabil sein.
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 26. Mai 2011 23:07 Titel: franz Verfasst am: 26. Mai 2011 23:07 Titel: |
 |
|
Das müßte der Extrempunkt des effektiven Potentials sein; als "singuläre" Lösung. Und der "Normalfall"? 
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 26. Mai 2011 23:11 Titel: Keplerfan Verfasst am: 26. Mai 2011 23:11 Titel: |
 |
|
|
Hm, warum singulär? Ist es keine gültige Lösung?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 26. Mai 2011 23:16 Titel: franz Verfasst am: 26. Mai 2011 23:16 Titel: |
 |
|
Die Lösung wird schon stimmen.
"Singulär" würde ich sagen, weil es sich um einen (instabilen) Sonderfall handelt. J (oder P) zum Beispiel ist ja nicht der Drehimpuls, sondern nur die z - Komponente. Bei geringer Abweichung beginnt meines Erachtens der "Normalbetrieb"...
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 26. Mai 2011 23:27 Titel: TomS Verfasst am: 26. Mai 2011 23:27 Titel: |
 |
|
Für konstantes r musst du dr/dt gleich Null setzen, nicht dE/dr
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 27. Mai 2011 18:08 Titel: Keplerfan Verfasst am: 27. Mai 2011 18:08 Titel: |
 |
|
Da ich nun nicht dafür verantwortlich sein will, dass dieser Thread an der ursprünglichen Fragestellung vorbeischrammt, sollte vielleicht vor der Diskussion über Kreisbahnen geklärt werden, wie man zu den Lagrange-Gleichungen gelangt.
Die verallgemeinerten Koordinaten sind in diesem Falle  und und  . Allgemein können diese Koordinaten alle Koordinaten sein, die Punkte auf dem Kreiskegel beschreiben, auf dem sich das Teilchen bewegt. Jede Parametrisierung der Kegeloberfläche liefert ein Paar gültiger verallgemeinerter Koordinaten. Die Idee von Lagrange-II ist nun, dass alle Zwangsbedingungen (nämlich hier: Teilchen bewegt sich auf dem Kegel) dadurch berücksichtigt sind, dass man eben solche Koordinaten wählt, die, egal wie man . Allgemein können diese Koordinaten alle Koordinaten sein, die Punkte auf dem Kreiskegel beschreiben, auf dem sich das Teilchen bewegt. Jede Parametrisierung der Kegeloberfläche liefert ein Paar gültiger verallgemeinerter Koordinaten. Die Idee von Lagrange-II ist nun, dass alle Zwangsbedingungen (nämlich hier: Teilchen bewegt sich auf dem Kegel) dadurch berücksichtigt sind, dass man eben solche Koordinaten wählt, die, egal wie man 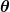 und und  wählt, immer nur Punkte auf dem Kreiskegel beschreiben. Du musst also, nachdem du die Lagrange-Funktion erhalten hast, einfach die Gleichung wählt, immer nur Punkte auf dem Kreiskegel beschreiben. Du musst also, nachdem du die Lagrange-Funktion erhalten hast, einfach die Gleichung
=\frac{\partial L}{\partial r}) aufschreiben. Dies ist dann deine Bewegungsgleichung für r. Genauso verfährst du für aufschreiben. Dies ist dann deine Bewegungsgleichung für r. Genauso verfährst du für 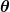 . Du musst . Du musst  und und  dabei bei der partiellen Ableitung als unabhängige Koordinaten betrachten, so als ob du z.B. einmal nach x und einmal nach y ableiten würdest. dabei bei der partiellen Ableitung als unabhängige Koordinaten betrachten, so als ob du z.B. einmal nach x und einmal nach y ableiten würdest.
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 27. Mai 2011 19:51 Titel: franz Verfasst am: 27. Mai 2011 19:51 Titel: |
 |
|
Möchte mich für mein Dazwischenquatschen entschuldigen! Andererseits gibt es, meiner Ansicht nach, bisher gar keine klare Fragestellung:
| Zitat: | | darf man für ein Teilchen .. auf der Innenseite eines Kreiskegels die potentielle Energie ... benutzen? |
Insofern hatte ich (neugierig) interpretiert: Wie bewegt sich ein Punkt in einem "Trichter"? [Und man erläutere nebenbei LAGRANGE II !] 
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 27. Mai 2011 20:04 Titel: Keplerfan Verfasst am: 27. Mai 2011 20:04 Titel: |
 |
|
Kein Problem, franz. 
Ich meinte diese, spätere, Frage:
| WhiteRussian hat Folgendes geschrieben: | Kommt ihr auch aus Freiburg oder macht ihr das nur zum Spaß 
Dass die letzte Komponente falsch war habe ich gesehen. Das muss natürlich ein Alpha sein.
Jetzt sollen wir aus dieser Funktion die Lagrangegleichung gewinnen. Ich habe leider nicht so ganz den Plan wie das geht, da ich das mit den verallgemeinerten Koordinaten nicht so ganz verstehe. |
|
|
 |
Netw
Gast
|
 Netw Verfasst am: 29. Jun 2013 20:53 Titel: Netw Verfasst am: 29. Jun 2013 20:53 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Deine Gleichungen stimmen m.E. nicht.
Wenn du die Gleichung für theta betrachtest, dann bekommst du ja

theta ist zyklisch.
Dann leitest du ab:

Die Zeitableitung angewandt auf diesen Term wirkt aber sowohl auf theta als auch auf r, d.h. dass eben nicht

sondern

OK?
Die Gleichung fürr musst du daraufhin ebenfalls nochmal prüfen.
Aber wie gesagt, ich denke, du kommst mittels des Einsetzens des erhaltenen Drehimpulses L in die erhaltene Energie E zu einer DGL. erster Ordnung - und das ist wesentlich leichter. |
der drehimplus der hier erhalten ist in welcher richtung zeigt er?
wenn der drehimplus erhalten ist muss doch die bewegung in einer ebene verlaufen?
|
|
 |
|
















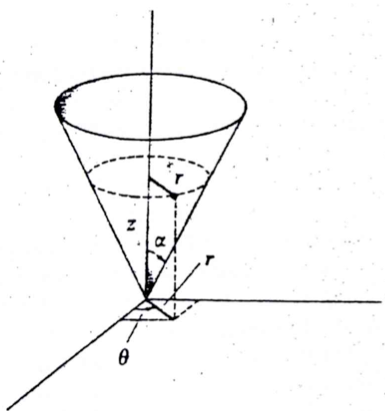

 Dort habe ich folgende Parametrisierung des Kegels gefunden:
Dort habe ich folgende Parametrisierung des Kegels gefunden:


