| Autor |
Nachricht |
Alex12345
Gast
|
 Alex12345 Verfasst am: 02. Sep 2014 12:13 Titel: Verteilung Wasserdruck Kugel Alex12345 Verfasst am: 02. Sep 2014 12:13 Titel: Verteilung Wasserdruck Kugel |
 |
|
Meine Frage:
Hallo zusammen,
auch nach einigen Versuchen mit Google bin ich mir nicht sicher, ob meine Überlegung(en) Sinn ergeben. Daher würde ich mich über einen kurzen Kommentar ggf. mit Verbesserung sehr freuen.
Es geht um ein Wehr in Kugelform. Dieses ist 3m hoch und auf der einen Seite steht das Wasser genau 3m hoch.
Was würde sich ändern, wenn die Kugel vollständig in Wasser getaucht würde?
Meine Ideen:
Ursprungsfrage: Verteilt sich der Wasserdruck nun ganz "normal" linear als Dreieck quasi?
Änderung: Die Horizontalkomponenten heben sich gegenseitig aus und für die Berechnung ist es dann Kreisfläche mal pgh (h=tiefste Stelle) ?
Danke euch!
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 02. Sep 2014 12:17 Titel: isi1 Verfasst am: 02. Sep 2014 12:17 Titel: |
 |
|
Das habe ich nicht verstanden, Alex,
wenn es ein Wehr ist, wie können sich die horizontalen Komponenten ausgleichen?
Hast Du eine Skizze von der Anordnung?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
Alex12345
Gast
|
 Alex12345 Verfasst am: 02. Sep 2014 12:24 Titel: Alex12345 Verfasst am: 02. Sep 2014 12:24 Titel: |
 |
|
Das ist auch ziemlich konfus formuliert, sorry. Generell geht es erstmal um ein Wehr, mit einer einseitigen Wasserdruckbelastung. Ist meine Vermutung, dass der Wasserdruck linear steigt, also als Dreieck gezeichnet werden kann richtig? Ich hatte Zweifel, da es sich ja nicht um eine glatte Ebene handelt.
Der zweite Teil war losgelöst von oben. Angenommen eine Kugel ist vollständig mit Wasser umgeben. Wie verteilt sich dann der Wasserdruck? Ich würde sagen: zwei lineare Verläufe links und rechts, die sich aufheben im Kräftegleichgewicht + eine vertikale Komponente (die sich mit Auftrieb+Normalkraft aufhebt).
Ich hoffe es ist nun verständlicher.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 02. Sep 2014 12:30 Titel: isi1 Verfasst am: 02. Sep 2014 12:30 Titel: |
 |
|
| Alex12345 hat Folgendes geschrieben: | | Ist meine Vermutung, dass der Wasserdruck linear steigt, also als Dreieck gezeichnet werden kann richtig? Ich hatte Zweifel, da es sich ja nicht um eine glatte Ebene handelt. |
Ja, Alex, das ist richtig, es hängt nur von der Wassertiefe ab, Druck p = g * Wassertiefe * Dichte
| Alex12345 hat Folgendes geschrieben: | | Der zweite Teil war losgelöst von oben. Angenommen eine Kugel ist vollständig mit Wasser umgeben. Wie verteilt sich dann der Wasserdruck? Ich würde sagen: zwei lineare Verläufe links und rechts, die sich aufheben im Kräftegleichgewicht + eine vertikale Komponente (die sich mit Auftrieb+Normalkraft aufhebt). |
Ja, stimmt auch. Auftrieb = Volumen * Dichte.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
Alex12345
Gast
|
 Alex12345 Verfasst am: 02. Sep 2014 12:42 Titel: Alex12345 Verfasst am: 02. Sep 2014 12:42 Titel: |
 |
|
Gut, danke. Dann habe ich noch eine Frage zum Angriffspunkt von F res.
"Um herauszufinden, durch welchen Punkt im Querschnitt des Wehrs, die resultierende Druckkraft des Wassers verläuft, überlegen Sie, welche Wirkungsrichtung die differenziellen Druckkräfte auf die Mantelfläche haben."
Mir ist es jetzt allerdings nicht ganz klar, wo das ist.
Beim Wehr (links Wasser): Fres wird in 1/3 der Tiefe von unten gesehen angreifen mit dem Betrag: roh * g *h * A. Ist die Fläche eine projizierte Kreisfläche mit pi*r^2?
Wo würde der Angriffspunkt bei einer Kugel liegen die vollständig in Wasser getaucht ist?
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 02. Sep 2014 12:52 Titel: isi1 Verfasst am: 02. Sep 2014 12:52 Titel: |
 |
|
Kann das stimmen mit dem Drittel der Höhe?
Du hast ja kein Rechteck, also wirkt der hohe Druck ganz unten nur auf einer kleinen Fläche und in der Mitte haben wir eine deutlich größere Fläche. Und Kraft ist doch bekanntlich Druck mal Fläche, oder?
Generell wirkt der Wasserdruck senkrecht auf das Flächenteilstück. Dies ist wichtig, wenn die Festigkeit der Kugel selbst betrachtet wird.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
Alex12345
Gast
|
 Alex12345 Verfasst am: 02. Sep 2014 12:56 Titel: Alex12345 Verfasst am: 02. Sep 2014 12:56 Titel: |
 |
|
|
Dann greift F mittig, also in h/2, an?
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 02. Sep 2014 14:26 Titel: isi1 Verfasst am: 02. Sep 2014 14:26 Titel: |
 |
|
| Alex12345 hat Folgendes geschrieben: | | Dann greift F mittig, also in h/2, an? |
Das glaube ich auch wieder nicht, Alex.
Integriere doch mal Druck*Fläche auf.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 02. Sep 2014 14:37 Titel: franz Verfasst am: 02. Sep 2014 14:37 Titel: |
 |
|
| isi1 hat Folgendes geschrieben: | | Hast Du eine Skizze von der Anordnung? |
Darum wollte ich auch gerade bitten. In Holland sah ich letztens viele interessante Anlagen, aber nix kugelförmiges.
|
|
 |
Alex12345
Gast
|
 Alex12345 Verfasst am: 02. Sep 2014 14:38 Titel: Alex12345 Verfasst am: 02. Sep 2014 14:38 Titel: |
 |
|
Das habe ich noch nie gemacht..
Ist das dieses Integral?

Aber was ist denn die Variable nach der integriert werden muss? Falls es x sein sollte, käme bei mir 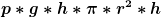 raus... raus...
|
|
 |
Alex12345
Gast
|
 Alex12345 Verfasst am: 02. Sep 2014 14:42 Titel: Alex12345 Verfasst am: 02. Sep 2014 14:42 Titel: |
 |
|
| franz hat Folgendes geschrieben: | | isi1 hat Folgendes geschrieben: | | Hast Du eine Skizze von der Anordnung? |
Darum wollte ich auch gerade bitten. In Holland sah ich letztens viele interessante Anlagen, aber nix kugelförmiges. |
fotos-hochladen.net/uploads/bildschirmfotoj25lkdpy6i.png
Kugel ist falsch... es sollte eher kreisförmig heißen, oder?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 02. Sep 2014 15:28 Titel: franz Verfasst am: 02. Sep 2014 15:28 Titel: |
 |
|
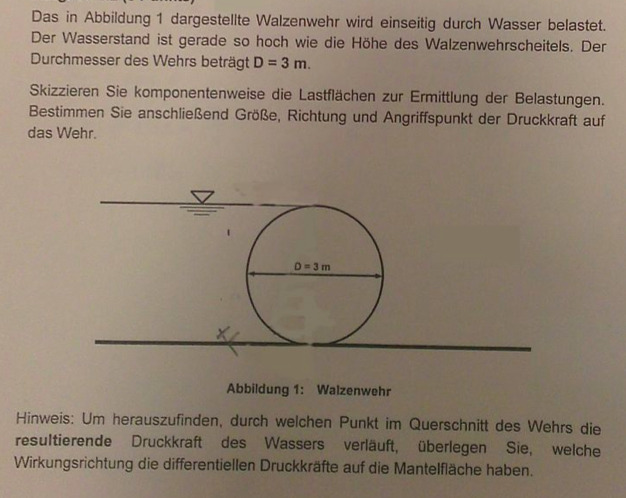
Wir nähern uns der Aufgabe :-)
| Beschreibung: |
|
| Dateigröße: |
74.58 KB |
| Angeschaut: |
4119 mal |
|
|
|
 |
jumi
Gast
|
 jumi Verfasst am: 02. Sep 2014 16:15 Titel: jumi Verfasst am: 02. Sep 2014 16:15 Titel: |
 |
|
Noch eine kleine Hilfe:
bisher wurde ja schon (nach seitenweiser Diskussion) erkannt, dass eine Walze keine Kugel ist. Sie sei eher kreisförmig!
Ich habe gelernt, eine Walze ist ein Körper, ein Kreis ein 2D-Gebilde.
Kurz: ich schlage vor, die Walze ist zylinderförmig.
Noch ein Tipp: die differentiellen Kräfte zeigen alle zur Zylinderachse.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 02. Sep 2014 16:52 Titel: isi1 Verfasst am: 02. Sep 2014 16:52 Titel: |
 |
|
Na ja, Walzenwehr, Alex,
dann stimmt das 1/3 der Höhe (für die waagrechten Kräfte), denn wir haben ein Rechteck (in der Mittelsenkrechten) der Walze.
Ich bin gespannt, was herauskommt, wenn man den Auftrieb (halbe Querschnittsfläche * Dichte, Schwerpunkt (0,212*r|r)) dazunimmt.
Hast Du Angaben zum Gewicht der Walze?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
jumi
Gast
|
 jumi Verfasst am: 02. Sep 2014 19:23 Titel: jumi Verfasst am: 02. Sep 2014 19:23 Titel: |
 |
|
Ich erhalte für den Angriffspunkt der resultierenden Kraft:
Tiefe = 2,43 m.
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 03. Sep 2014 05:22 Titel: franz Verfasst am: 03. Sep 2014 05:22 Titel: |
 |
|
| isi1 hat Folgendes geschrieben: | | Ich bin gespannt, was herauskommt, wenn man den Auftrieb [...] |
Ist nicht der Auftrieb schon in der resultierenden Druckkraft enthalten? Oder meinst Du die Resutierende (Auftrieb + Gewicht)?
| jumi hat Folgendes geschrieben: | Ich erhalte für den Angriffspunkt der resultierenden Kraft:
Tiefe = 2,43 m. |
d'accord*) :-)
Aus baulicher Sicht spielt vermutlich das enstprechende Drehmoment eine wichtige Rolle(?).
---------------------------------------------------------------------------------------
*) Meine vermutlich ähnliche Überlegung dazu: x und y-Achse wie üblich, Winkel phi y-Achse gegen den jeweiligen Radiusvektor, Walzenbreite L, Radius R = 1,5 m, Flächen A, Tiefe gegen Oberfläche Delta y, Druck p, Kraft F:
=R(1-cos\varphi);\ p=\rho g \Delta y)
=pdA=\rho g R^2L(1-cos\varphi)d\varphi)
=dF(\varphi)\cdot sin\varphi;\ dF_y(\varphi)=dF(\varphi)\cdot (-cos\varphi))
Integriert von 0 bis pi ->
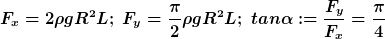
Die Richtung der Druckkraft auf die Achse der Walze ergibt einen äußeren Angriffspunkt in eine Höhe h gegen Grund
=R\left(1-sin\ arctan\frac{\pi}{4}\right)\approx 0{,}57\ m)
|
|
 |
jumi
Gast
|
 jumi Verfasst am: 03. Sep 2014 07:27 Titel: jumi Verfasst am: 03. Sep 2014 07:27 Titel: |
 |
|
| franz hat Folgendes geschrieben: | | Aus baulicher Sicht spielt vermutlich das enstprechende Drehmoment eine wichtige Rolle(?). |
Welches Drehmoment denn ?
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 03. Sep 2014 08:50 Titel: isi1 Verfasst am: 03. Sep 2014 08:50 Titel: |
 |
|
| franz hat Folgendes geschrieben: | | Ist nicht der Auftrieb schon in der resultierenden Druckkraft enthalten? Oder meinst Du die Resutierende (Auftrieb + Gewicht)? |
Sicher, Franz,
ich hatte waagrechte und senkrechte Kräfte getrennt berechnet. 
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 03. Sep 2014 09:07 Titel: franz Verfasst am: 03. Sep 2014 09:07 Titel: |
 |
|
| jumi hat Folgendes geschrieben: | | Welches Drehmoment denn ? |
 Gute Frage! Gute Frage!
Die auftretenden Momente müssen sich natürlich aufheben.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
|
 |
jumi
Gast
|
 jumi Verfasst am: 03. Sep 2014 11:09 Titel: jumi Verfasst am: 03. Sep 2014 11:09 Titel: |
 |
|
Der Grund weshalb solche Walzenwehre überhaupt trotz Herstellungsschwierigkeiten gebaut werden, ist, dass eben keine Drehmomente auftreten!
Ich rechne mal die Methode (ohne Integral) :
(für Walzenlänge = 1 m)
Horizontale Kraft: (=Kraft auf die Projektionsfläche)
^2}{2}=44145 N)
Vertikale Kraft (=Gewichtskraft des Wasser in der halben Walze)
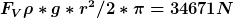
Gesamtkraft F:

Richtung dieser Kraft geht durch den Mittelpunkt des Walzenquerschnitts.
Neigung der Kraftrichtung = phi arctan(FH/FV) = 0,9050 (gegen Vertikale)
Der Angriffspunkt dieser Kraft liegt daher in der Tiefe=r+r*cos(phi)=2,43 m.
|
|
 |
jumi
Gast
|
 jumi Verfasst am: 03. Sep 2014 11:11 Titel: jumi Verfasst am: 03. Sep 2014 11:11 Titel: |
 |
|
kleiner Tippfehler:
Neigung der Kraftrichtung phi = arctan(FH/FV) = 0,9050 (gegen Vertikale)
|
|
 |
Alex12345
Gast
|
 Alex12345 Verfasst am: 03. Sep 2014 13:14 Titel: Alex12345 Verfasst am: 03. Sep 2014 13:14 Titel: |
 |
|
Super, perfekt vielen Dank euch allen!
Sorry für die undeutliche Formulierung, nächstes Mal direkt mit Foto!
|
|
 |
|


















 Gute Frage!
Gute Frage!