| Autor |
Nachricht |
Bodo85
Anmeldungsdatum: 18.10.2013
Beiträge: 9
|
 Bodo85 Verfasst am: 18. Okt 2013 17:14 Titel: Frequenz berechnen einer harmonischen Schwingung Bodo85 Verfasst am: 18. Okt 2013 17:14 Titel: Frequenz berechnen einer harmonischen Schwingung |
 |
|
Guten Tag,
Ich brauche mal einen Gedankenanstoß.
Ich sitze gerade vor einer Aufgabe, in der es um die harmonische Schwingung geht. Laut Aufgabe habe ich ein Schüttelsieb, welches auf und ab bewegt wird, damit sich die darin enthaltenen Steine lösen. Als Wert ist mir  gegeben. gegeben.
Mein Ansatz...
Bisher habe ich mir die Schwingung aufgezeichnet...
Also eine Skizze angefertigt. Mir fehlen allerdings noch ein paar Werte um irgendwie weiter zu kommen.
Mein bisheriger Gedanke besagt, das  wohl die Amplitude wohl die Amplitude  ist. ist.
Mein Gedanke war es folgende Formel zu verwenden um die Frequenz herauszubekommen:
)
Das ist aber irgendwie nur der Input den ich meine zu nehmen...
Von der Logik her würde ich versuchen die Frequenz zu berechnen
 um dann die Kreisfrequenz zu berechnen um dann die Kreisfrequenz zu berechnen 
Dann allerdings kann ich  nicht verwenden. nicht verwenden.
Es sei denn ich würde die o.g. Formel verwenden und das  einsetzen... einsetzen...
Mir fehlt irgendwie die Idee...
Ich hoffe auf Hilfe!
Viele Grüße
Bodo |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 18. Okt 2013 17:19 Titel: Steffen Bühler Verfasst am: 18. Okt 2013 17:19 Titel: |
 |
|
Willkommen im Physikerboard!
Was sollst Du laut Aufgabe denn tun? Und was ist außer xm gegeben? Hast Du zufällig den genauen Wortlaut der Aufgabe?
Viele Grüße
Steffen |
|
 |
Bodo85
Anmeldungsdatum: 18.10.2013
Beiträge: 9
|
 Bodo85 Verfasst am: 18. Okt 2013 17:24 Titel: Bodo85 Verfasst am: 18. Okt 2013 17:24 Titel: |
 |
|
Vielen Dank für die Begrüßung 
Die Aufgabe lautet:
Ein Schüttelsieb führt eine senkrechte Bewegung (hamonische Schwingung) mit der Amplitude  aus. Wie groß ist die Frequenz, damit Steine, die auf dem Sieb liegen, sich von dem Sieb lösen? aus. Wie groß ist die Frequenz, damit Steine, die auf dem Sieb liegen, sich von dem Sieb lösen?
 |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 18. Okt 2013 17:44 Titel: Steffen Bühler Verfasst am: 18. Okt 2013 17:44 Titel: |
 |
|
|
Gut. Hast Du eine Idee, was die Bedingung ist, dass sich die Steine vom Sieb lösen? |
|
 |
Bodo85
Anmeldungsdatum: 18.10.2013
Beiträge: 9
|
 Bodo85 Verfasst am: 18. Okt 2013 17:48 Titel: Bodo85 Verfasst am: 18. Okt 2013 17:48 Titel: |
 |
|
Ich denke, dass man eine bestimmte Freuqenz mit einem bestimmten Ausschlag benötigt.
Wenn ich ein Sieb auf und ab bewege, muss man meiner Meinung nach noch die Erdbeschleunigung einberechnen, da man ja schneller als diese sein muss, damit die Steine abheben können. |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 18. Okt 2013 17:55 Titel: Steffen Bühler Verfasst am: 18. Okt 2013 17:55 Titel: |
 |
|
Völlig richtig. Du musst schneller als die Erdbeschleunigung werden.
Und Dein Ansatz ) ist auch in Ordnung. Das ist die Gleichung für den Weg, den das Sieb in der Zeit zurücklegt. Die Anfangsphase brauchen wir nicht, und die Amplitude ymax heißt bei uns xm. Somit gilt für den Weg des Siebs: ist auch in Ordnung. Das ist die Gleichung für den Weg, den das Sieb in der Zeit zurücklegt. Die Anfangsphase brauchen wir nicht, und die Amplitude ymax heißt bei uns xm. Somit gilt für den Weg des Siebs:
=x_m \cdot \sin (\omega \cdot t))
Nun brauchen wir aber nicht den Weg, sondern die Beschleunigung des Siebs. Was tun? |
|
 |
Bodo85
Anmeldungsdatum: 18.10.2013
Beiträge: 9
|
 Bodo85 Verfasst am: 18. Okt 2013 18:07 Titel: Bodo85 Verfasst am: 18. Okt 2013 18:07 Titel: |
 |
|
Ich glaube mir fällt es gleich wie Schuppen von den Augen!
a = Erdbeschleunigung = 
Jetzt habe ich mal in meine schlaue Formelsammlung geguckt... und da steht

Wenn ich diese Formel nehme und umwandel in

... dann hätte ich meine Frequenz... , die Kreisfrequenz?!
Die Phase setze ich dann Null, da ich die ja nicht benöige... D.h. einfach rausnehmen, oder? |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 18. Okt 2013 18:14 Titel: Steffen Bühler Verfasst am: 18. Okt 2013 18:14 Titel: |
 |
|
Du bist schon nah dran. Allerdings ist es mir nicht ganz klar, was hier dieses  sein soll. Dir vielleicht? sein soll. Dir vielleicht?
Aber auch ohne Formelsammlung solltest Du durch einfaches Ableiten von x(t) auf die Formel für a(t) kommen, oder? Da kommt fast dasselbe raus...
Und da der Sinus bekanntermaßen maximal Eins wird, kannst Du so in der Tat die Frequenz berechnen, bei der die maximale Beschleunigung die Erdbeschleunigung ist. |
|
 |
Bodo85
Anmeldungsdatum: 18.10.2013
Beiträge: 9
|
 Bodo85 Verfasst am: 18. Okt 2013 18:41 Titel: Bodo85 Verfasst am: 18. Okt 2013 18:41 Titel: |
 |
|
Beim Schiffeversenken spielen würde ich jetzt sagen: "Du hast meinen Flugzeugträger versenkt!"
Ableitungen und Aufleitungen sind meine nächste Baustelle....
Von dem was ich mitbekommen habe, könnte ich sin ersetzen mit cos ?!
Das ist mir jetzt richtig unangenehm... |
|
 |
Bodo85
Anmeldungsdatum: 18.10.2013
Beiträge: 9
|
 Bodo85 Verfasst am: 18. Okt 2013 19:35 Titel: Bodo85 Verfasst am: 18. Okt 2013 19:35 Titel: |
 |
|
Ich habe es glaube ich... so lernt man nebenbei auch noch zwangsläufig das Ableiten 
=x_m*\sin(\omega*t*\varphi) )
=x_m*\cos(\omega*t)*\omega)
=x_m*-\sin(\omega*t)*\omega^2 )
) umgestellt: umgestellt:

) fällt raus, da fällt raus, da  und und  = 0) ; das "-" wird dann vorgezogen. ; das "-" wird dann vorgezogen. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 18. Okt 2013 20:54 Titel: GvC Verfasst am: 18. Okt 2013 20:54 Titel: |
 |
|
| Bodo85 hat Folgendes geschrieben: | Ich habe es glaube ich... so lernt man nebenbei auch noch zwangsläufig das Ableiten ;)
=x_m*\sin(\omega*t*\varphi) )
=x_m*\cos(\omega*t)*\omega)
=x_m*-\sin(\omega*t)*\omega^2 ) |
Das ist wirklich noch eine Baustelle.
| Zitat: | ) umgestellt: umgestellt:
 |
Die Bedingung ist doch  . Wenn Du das einsezt, was bekommst Du dann raus? . Wenn Du das einsezt, was bekommst Du dann raus?
| Zitat: | ) fällt raus, da fällt raus, da  und und  = 0) |
Wenn Du schon weißt, dass 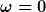 ist (was falsch ist), dann brauchtest Du das ja nicht mehr zu berechnen. Übrigens: Wie groß ist ein Bruch, dessen Nenner Null ist? ist (was falsch ist), dann brauchtest Du das ja nicht mehr zu berechnen. Übrigens: Wie groß ist ein Bruch, dessen Nenner Null ist?
Steffen Bühler hat Dir doch schon alles haarklein erklärt.
Zuletzt bearbeitet von GvC am 18. Okt 2013 21:02, insgesamt einmal bearbeitet |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 18. Okt 2013 21:02 Titel: Steffen Bühler Verfasst am: 18. Okt 2013 21:02 Titel: |
 |
|
| Bodo85 hat Folgendes geschrieben: | =x_m*-\sin(\omega*t)*\omega^2 ) |
Bis hierher vollkommen in Ordnung. Nun aber muss noch mal ein Gedanke verschwendet werden an die Frage, wann a(t) am größten ist. Denn erst, wenn a(t) größer als die Erdbeschleunigung ist, lösen sich die Steinchen vom Sieb!
Da hilft, wie geschrieben, das Wissen um die Wertemenge einer Sinusfunktion: die schwankt ja nur zwischen -1 und 1. Somit wird a(t) am größten, wenn der Sinus in der Formel den Wert -1 annimmt. Dann nämlich wird =a_{max}=x_m \cdot \omega^2 )
Und das war's fast schon. Jetzt musst Du nur noch die Frequenz ausrechnen.
Viele Grüße
Steffen |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 18. Okt 2013 21:05 Titel: GvC Verfasst am: 18. Okt 2013 21:05 Titel: |
 |
|
|
Es ändert zwar nichts am Ergebnis, dennoch sind die Ableitungen von Bodo85 falsch. |
|
 |
Bodo85
Anmeldungsdatum: 18.10.2013
Beiträge: 9
|
 Bodo85 Verfasst am: 18. Okt 2013 21:17 Titel: Bodo85 Verfasst am: 18. Okt 2013 21:17 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Es ändert zwar nichts am Ergebnis, dennoch sind die Ableitungen von Bodo85 falsch. |
Verstehe ich nicht? Wieso denn? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 18. Okt 2013 21:38 Titel: GvC Verfasst am: 18. Okt 2013 21:38 Titel: |
 |
|
| Bodo85 hat Folgendes geschrieben: | | GvC hat Folgendes geschrieben: | | Es ändert zwar nichts am Ergebnis, dennoch sind die Ableitungen von Bodo85 falsch. |
Verstehe ich nicht? Wieso denn? |
Zunächst mal ist die Ausgangsfunktion für x(t) verkehrt. Du hast geschrieben
| Bodo85 hat Folgendes geschrieben: | =x_m*\sin{(\omega*t*\varphi)}) |
Richtig wäre
=x_m\cdot\sin{(\omega t+\varphi)})
Und davon ist die Ableitung laut Kettenregel (äußere Ableitung mal innere Ableitung)
=x_m\cdot\cos{(\omega t+\varphi)}\cdot\omega)
Wo ist bei Dir der Nullphasenwinkel  geblieben? geblieben?
und die zweite Ableitung (nach derselben Regel)
=-x_m\cdot\sin{(\omega t+\varphi)}\cdot\omega^2)
Wie gesagt, das spielt für diese Aufgabe keine Rolle, da Du nur am Maximum des Sinus interessiert bist. Und der ist unabhängig von  immer 1 (übrigens nicht -1, wie Steffen Bühler gesagt hat, denn die Steine heben im oberen Umkehrpunkt ab, nicht im unteren; dafür ist a nach oben gerichtet, g dagegen nach unten, hat also ein anderes Vorzeichen). immer 1 (übrigens nicht -1, wie Steffen Bühler gesagt hat, denn die Steine heben im oberen Umkehrpunkt ab, nicht im unteren; dafür ist a nach oben gerichtet, g dagegen nach unten, hat also ein anderes Vorzeichen). |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 18. Okt 2013 21:46 Titel: Steffen Bühler Verfasst am: 18. Okt 2013 21:46 Titel: |
 |
|
Nun, Du hattest noch ein überflüssiges 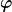 in Deiner ersten Gleichung, noch dazu multiplikativ verknüpft. Ich habe das galant ignoriert. Das ist ja die Startphase, die wird natürlich addiert. Und wenn Du sie partout nicht auf Null setzen willst, wie ich empfohlen habe, musst Du sie natürlich mit ableiten, sie kommt dann ins Argument in den Cosinus bzw Minus-Sinus. in Deiner ersten Gleichung, noch dazu multiplikativ verknüpft. Ich habe das galant ignoriert. Das ist ja die Startphase, die wird natürlich addiert. Und wenn Du sie partout nicht auf Null setzen willst, wie ich empfohlen habe, musst Du sie natürlich mit ableiten, sie kommt dann ins Argument in den Cosinus bzw Minus-Sinus.
Das ist eben das, worauf es in der Tat in der Mathematik und Physik (wie auch im restlichen Leben) ankommt: Sorgfalt und Konzentration.
Streicht man das 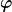 einfach weg, stimmt allerdings alles. Denn bei der inneren Ableitung wird es ja zu Null, und wir interessieren uns ja nur für den Faktor vor der Sinusschwingung. einfach weg, stimmt allerdings alles. Denn bei der inneren Ableitung wird es ja zu Null, und wir interessieren uns ja nur für den Faktor vor der Sinusschwingung. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 18. Okt 2013 21:55 Titel: GvC Verfasst am: 18. Okt 2013 21:55 Titel: |
 |
|
| Steffen Bühler hat Folgendes geschrieben: | Streicht man das  einfach weg, stimmt allerdings alles. einfach weg, stimmt allerdings alles. |
Es stimmt auch alles, wenn man das nicht wegstreicht. Wie gesagt, es ändert nichts am Ergebnis, da man nur am Maximum des Sinus interessiert ist. Wenn das  aber in der Gleichung für die Auslenkung nicht weggestrichen wird (Bodo85 hat es nicht weggestrichen), dann darf es auch in den Ableitungen nicht weggestrichen werden. aber in der Gleichung für die Auslenkung nicht weggestrichen wird (Bodo85 hat es nicht weggestrichen), dann darf es auch in den Ableitungen nicht weggestrichen werden. |
|
 |
Bodo85
Anmeldungsdatum: 18.10.2013
Beiträge: 9
|
 Bodo85 Verfasst am: 20. Okt 2013 12:55 Titel: Bodo85 Verfasst am: 20. Okt 2013 12:55 Titel: |
 |
|
So nach einer kleinen Pause bin nun endlich auch auf das Ergebnis gekommen.
Erstmal habe ich einen Fehler in der Formel gehabt.
Die Normalform der Formel lautet:
=y_{max} sin(\omega t + \varphi))
Diese Formel wurde dann in folgende abgeleitet:
(von der Strecke abgeleitet in die Geschwindigkeit und dann in die Beschleunigung)
=-y_{max} sin(\omega t + \varphi) \omega^2)
da nun 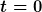 ist, da wir uns am Anfang der Bewegung befinden. Am Punkt ist, da wir uns am Anfang der Bewegung befinden. Am Punkt 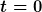 . .
also lautet die Formel nun:

^2)
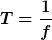
daraus folgt also :
^2)
umgestellt nach f (da wir de Frequenz haben wollen...):



Nur noch einsetzen und wir haben das Ergebnis!

die Frequenz muss als größer sein als 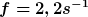
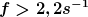
Vielen Dank für eure Hilfe. Hier dürfte jetzt kein Fehler mehr sein! |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 21. Okt 2013 08:42 Titel: Steffen Bühler Verfasst am: 21. Okt 2013 08:42 Titel: |
 |
|
Das Ergebnis ist richtig, aber bei der Herleitung bin ich nicht einverstanden.
| Bodo85 hat Folgendes geschrieben: | =-y_{max} sin(\omega t + \varphi) \omega^2)
da nun 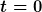 ist, da wir uns am Anfang der Bewegung befinden. Am Punkt ist, da wir uns am Anfang der Bewegung befinden. Am Punkt 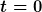 . .
also lautet die Formel nun:
 |
Hier stimmen zwei Sachen nicht. Wenn Du in die Formel oben t=0 einsetzt, bleibt immer noch die Unbekannte  im Argument des Sinus. So kommst Du also nicht weiter. im Argument des Sinus. So kommst Du also nicht weiter.
Vor allem kannst Du durch t=0 nicht erwarten, dass Du den Sinusterm jetzt einfach wegstreichen kannst!
Außerdem willst Du ja das maximale a haben. Und es ist überhaupt nicht gesagt, dass dieses bei t=0 vorliegt!
Insgesamt ist diese Argumentationskette es also recht kühn. Um das Maximum von a(t) zu finden, muss man anders vorgehen. Ein umständlicher Weg wäre, den Hochpunkt durch weiteres Ableiten zu finden. Nun, und der elegantere Weg ist halt, wie bereits mehrfach erwähnt, sich zu überlegen, was das Maximum eines Sinus eigentlich ist. Denn dann kannst Du auf Anhieb die Maximalwerte einer Gleichung wie =42 \cdot sin(78! \cdot e^{4711x+x^{78}})) angeben, nicht wahr? angeben, nicht wahr?
Viele Grüße
Steffen |
|
 |
|
















