| Autor |
Nachricht |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 01. Jun 2013 12:02 Titel: Drehimpuls in Krummlinigen Koordinaten SunB Verfasst am: 01. Jun 2013 12:02 Titel: Drehimpuls in Krummlinigen Koordinaten |
 |
|
Hallo,
ich habe nun schon das Internet durchsucht, leider nichts richtiges gefunden.
Ich brauche den Drehimpuls in Polarkoordinaten, Zylinderkoordinaten und in Kugelkoordinaten.
Im Internet stand, wenn etwas zu finden war, dass z.B. der Drehimpuls in Kugelkoordinaten so aussieht:
^2 \dot{\varphi} \vec{e}_z)
Das kann aber doch nicht sein, da die Einheitsvektoren in Kugelkoordinaten ja
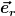 und und  und und  sind. sind.
Könntet ihr mit mir die mal berechnen? Ich brauche das für ein Referat über andere Koordinatensysteme...
Danke und Grüße
SunB |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 01. Jun 2013 12:26 Titel: pressure Verfasst am: 01. Jun 2013 12:26 Titel: |
 |
|
Warum berechnest du sie dir nicht selber
) ? ?
Also zunächst schreibst du dir 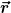 im entsprechend Koordinatensystem auf und berechnest anschließend unter Anwendung der mehrdimensionalen Kettenregel dessen Zeitableitung. Hierbei musst du beachten, dass die totale Zeitableitung der Basisvektoren z.B. von im entsprechend Koordinatensystem auf und berechnest anschließend unter Anwendung der mehrdimensionalen Kettenregel dessen Zeitableitung. Hierbei musst du beachten, dass die totale Zeitableitung der Basisvektoren z.B. von  aufgrund der Winkelabhängigkeit im Allgemeinen von Null verschieden sind. aufgrund der Winkelabhängigkeit im Allgemeinen von Null verschieden sind. |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 01. Jun 2013 17:14 Titel: SunB Verfasst am: 01. Jun 2013 17:14 Titel: |
 |
|
Da liegt ja mein Problem:
z.B. in Kugelkoordinaten:

und
 \dot{\varphi}\vec{e}_{\varphi})
Also:
 \dot{\varphi}\vec{e}_{\varphi})
Und nun? Muss jetzt  mit jedem Summand von mit jedem Summand von 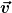 multipliziert werden? multipliziert werden? |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 01. Jun 2013 17:28 Titel: pressure Verfasst am: 01. Jun 2013 17:28 Titel: |
 |
|
Einverstanden, du hast nur die Klammer vergessen.
)
Und nun musst das Kreuzprodukt zwischen 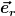 und allen drei Einheitsvektoren ausrechnen, dabei kannst du z.B. verwenden, dass und allen drei Einheitsvektoren ausrechnen, dabei kannst du z.B. verwenden, dass  ein rechtshändiges Dreibein bilden. ein rechtshändiges Dreibein bilden. |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 01. Jun 2013 17:35 Titel: SunB Verfasst am: 01. Jun 2013 17:35 Titel: |
 |
|
Ich bin Schüler...heißt, dass ich zwar aus Interesse (nicht wegen der Schule) das Kreuzprodukt in kartesischen Koordinaten kenne, jedoch wie soll das mit den Krummlinigen gehen?
Ich weiß, dass unterschiedliche Enheitsvektoren im Kreuzprodukt immer den 3 fehlenden ergeben. |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 01. Jun 2013 17:39 Titel: pressure Verfasst am: 01. Jun 2013 17:39 Titel: |
 |
|
Du kannst jederzeit für einen Zwischenschritt in kartesische Koordinaten übergehen, also z.B.

und das Kreuzprodukt, wie gewohnt berechnen. |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 01. Jun 2013 19:22 Titel: SunB Verfasst am: 01. Jun 2013 19:22 Titel: |
 |
|
Naja, dann gilt doch:
1. 
2. 
3. \dot{\varphi} \vec{e_{\theta}})
Also:
 \dot{\varphi} \vec{e_{\theta}})
Für Kugelkoordinaten? |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 01. Jun 2013 19:28 Titel: pressure Verfasst am: 01. Jun 2013 19:28 Titel: |
 |
|
Einverstanden  |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 02. Jun 2013 12:41 Titel: SunB Verfasst am: 02. Jun 2013 12:41 Titel: |
 |
|
Ok, wunderbar.
Bei Polarkoordinaten habe ich ja das Problem, dass das Kreuzprodukt nur für 3-DIm definiert ist. Wie mache ich das da?
Dann noch Zylinderkoordinaten:

und

Ergibt also:
 \times (\dot{\rho} \vec{e_{\rho}} + \rho \dot{\varphi} \vec{e_{\varphi}} + \dot{z} \vec{e_{z}}))
Und nun? Muss ich hier dann die KLammer "ausmultiplizieren"?
Also:

+

+

+

+

+

Insgesamt, ohne mal "m" also:

Drehimpuls in Zylinderkoordinaten also:

Stimmt das? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 02. Jun 2013 14:28 Titel: TomS Verfasst am: 02. Jun 2013 14:28 Titel: |
 |
|
| SunB hat Folgendes geschrieben: | | Bei Polarkoordinaten habe ich ja das Problem, dass das Kreuzprodukt nur für 3-DIm definiert ist. Wie mache ich das da? |
Das ist recht einfach. Du benutzt zunächst 3-dim. Zylinderkoorinaten. Die Bewegung findet jedoch ausschließlich in der xy-Ebene statt, d.h. der Drehimpuls hat lediglich eine z-Komponente und ist damit letztlich nur eine Zahl.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 02. Jun 2013 14:35 Titel: SunB Verfasst am: 02. Jun 2013 14:35 Titel: |
 |
|
Das heißt, ich nehme meinen Drehimpuls aus Zylinderkoordinaten und sage, da nur xy-Ebene bei Polarkoordinaten, ist dann nur in Z-Richtung zu betrachten.
Stimmt mein Drehimpuls aus meinem Post vorher in Zylinderkoordinaten?
Dann wäre mein Drehimpuls in Polarkoordinaten:

Oder? |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 02. Jun 2013 16:14 Titel: pressure Verfasst am: 02. Jun 2013 16:14 Titel: |
 |
|
Der Drehimpuls in Zylinderkoordinaten stimmt nicht ganz, auch ein Komponente in Richtung von  tritt auf! tritt auf!
Der Drehimpuls in Polarkoordinaten ist in Ordnung, wobei du eigentlich kein Vektor brauchst, zumal dieser Vektor nicht in dem betrachteten Vektorraum (der Ebene) liegt. Der Drehimpuls Ebene ist hier nur eine Zahl. |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 02. Jun 2013 16:21 Titel: SunB Verfasst am: 02. Jun 2013 16:21 Titel: |
 |
|
Ok, danke. Dann stimmt das ganze in Polarkoordinaten wenigstens.
Könntest du mir den Drehimpuls in Zylinderkoordinaten mal vorrechnen?
Ich finde meinen Fehler irgendwie nicht.... 
Es gilt doch?:
 |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 02. Jun 2013 17:20 Titel: SunB Verfasst am: 02. Jun 2013 17:20 Titel: |
 |
|
Vielleicht habe ich ihn gefunden, den Fehler...
Falls das aber hier nun auch nicht richtig ist für den Drehimpuls in Zylinderkoordinaten, dann weiß ich wirklich nicht mehr weiter....
Also:
 \vec{e_{\varphi}} + \rho^2 \dot{\varphi} \vec{e_z})
Sieht komisch aus...
Stimmt's nun? Falls nicht, dann bitte ich um freundliches Vorrechnen... |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 02. Jun 2013 17:44 Titel: pressure Verfasst am: 02. Jun 2013 17:44 Titel: |
 |
|
Bei deinem letzten Ausdruck fehlt die Masse und ein "Punkt" über  im zweiten Term. im zweiten Term. |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 02. Jun 2013 17:57 Titel: SunB Verfasst am: 02. Jun 2013 17:57 Titel: |
 |
|
Ok, dass heißt also so muss es lauten (die Masse habe ich tatsächlich vergessen):
\vec{e_{\varphi}} + m \rho^2 \dot{\varphi} \vec{e_z})
So nun müsste es stimmen? |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 02. Jun 2013 18:00 Titel: pressure Verfasst am: 02. Jun 2013 18:00 Titel: |
 |
|
Sieht gut aus  |
|
 |
SunB
Anmeldungsdatum: 17.05.2013
Beiträge: 19
|
 SunB Verfasst am: 02. Jun 2013 19:18 Titel: SunB Verfasst am: 02. Jun 2013 19:18 Titel: |
 |
|
Danke sehr.
Kennst du eigentlich noch eine Summen-Schreibweise, wie ich die Kreuzprodukte der Einheitsvektoren ausdrücken kann?
Ich komme immer durcheinander, ob nun + oder -. Gibt es da nicht eine Summenschreibweise für? |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 02. Jun 2013 20:11 Titel: pressure Verfasst am: 02. Jun 2013 20:11 Titel: |
 |
|
In kartesischen Koordinaten gilt
 , ,
wobei  das Levi-Civita-Symbol ist. Mit Summenkonvention kann man das auch kurz das Levi-Civita-Symbol ist. Mit Summenkonvention kann man das auch kurz  notieren, dabei wird über doppelte Indizes summiert. notieren, dabei wird über doppelte Indizes summiert.
Für orthogonale Koordinaten Systeme gilt das ganz analog, wenn du deine drei Einheitsvektoren so ordnest, dass sie ein (rechtshändiges Dreibein) bilden.
Das Vorzeichen kannst du dir übrigens auch relativ schnell mit der Rechten-Hand-Regel klar machen. |
|
 |
|

















