| Autor |
Nachricht |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 21. Jul 2012 17:33 Titel: Perle auf Draht, unterschiedliche Zwangsbedingungen Nima93 Verfasst am: 21. Jul 2012 17:33 Titel: Perle auf Draht, unterschiedliche Zwangsbedingungen |
 |
|
Meine Frage:
Hallo,
Habe schon wieder ein Problemchen. Ich muss die Zwangsbedingungen und Lagrange 1 für eine Perle aufstellen, die reibungsfrei auf einem Draht im Schwerefeld gleitet, der im Koordinatenzursprung verankert ist, einen konstanten Winkel Theta zur z-Achse hat und mit phi'=w um diese rotiert.
Für die Zwangsbedingungen habe ich jetzt
-y = 0
<br />
<br />
z²tan²(\theta) - x²-y² = 0
<br />
)
und damit ganz normal die Zwangskräfte bestimmt. Allerdings kommt für die eine Zwangskraft
 \end{pmatrix} )
heraus. Wenn ich jetzt, wie in der einer Teilaufgabe verlangt, Theta = Pi/2 setze, ist der Tangens ja nicht definiert. auch wenn man vorher die Transformationsformeln
cos(\phi)
<br />
y=r*sin(\theta)sin(\phi)
<br />
z=r*cos(\theta)
<br />
)
einsetzt, schafft das keine Abhilfe.
Jetzt habe ich herausgefunden, dass man als Zwangsbedingung statt
 - x²-y² = 0)
=0)
verwenden soll. So bekomme ich auch das richtige Ergebnis heraus, aber ich verstehe eifach nicht, warum die andere Zwangsbedingung falsch sein soll. Es müsste doch eigentlich das gleiche herauskommen, egal welche Bedingung ich wähle?
viele Grüße
Nima93
Meine Ideen:
. |
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 21. Jul 2012 18:30 Titel: eva1 Verfasst am: 21. Jul 2012 18:30 Titel: |
 |
|
Ich verstehe nicht wie du auf deine Zwangsbedingung kommst.
Wenn man einfach Kugelkoordianten nimmt, dann kann man sich einfach vorstellen, dass 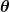 konstant ist und konstant ist und  . .
r variiert. |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 21. Jul 2012 23:15 Titel: Nima93 Verfasst am: 21. Jul 2012 23:15 Titel: |
 |
|
|
Wir sollen es zuerst in kartesischen Koordinaten machen. Stimmt, mit Kugel- oder Zylinderkoordinaten ginge es natürlich viel schneller... |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 22. Jul 2012 00:16 Titel: Nima93 Verfasst am: 22. Jul 2012 00:16 Titel: |
 |
|
Ich hab grade versucht, das ganze in Zylinderkoordinaten zu rechnen und bin leider kläglich gescheitert  Wahrscheinlich steh ich wieder mal völlig auf dem Schlauch... könnte mir jemand mal kurz erklären, was ich dann anders machen muss, als in kartesischen Koordinaten? Klar, ich muss die Formel für die Geschwindikeit in Zylinderkoordinaten in die Bewegungsgleichung einsetzen. Aber wie rechne ich die Zwangskräfte aus? Wahrscheinlich steh ich wieder mal völlig auf dem Schlauch... könnte mir jemand mal kurz erklären, was ich dann anders machen muss, als in kartesischen Koordinaten? Klar, ich muss die Formel für die Geschwindikeit in Zylinderkoordinaten in die Bewegungsgleichung einsetzen. Aber wie rechne ich die Zwangskräfte aus? |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 22. Jul 2012 07:52 Titel: franz Verfasst am: 22. Jul 2012 07:52 Titel: |
 |
|
Kuypers, Klassische Mechanik, behandelt mehrere Drahtperlenprobleme (dieses aber wohl nicht) mit Zwangskräften bzw. dem d'Alembert-Prinzip.
Traditionell gerechnet ergibt sich das interessante Problem

Siehe auch Seite 63 (leider ohne Schwerkraft) oder hier, insbesondere das .  |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 22. Jul 2012 10:10 Titel: Nima93 Verfasst am: 22. Jul 2012 10:10 Titel: |
 |
|
Vielen Dank, das hat mir in Bezug auf die Zylinderkoordinaten schonmal viel weitergeholfen. Hätte garnicht gedacht, dass dieses Problem so einen interessanten Hintergrund hat 
Aber meine anfängliche Frage, warum in kartesischen Koordinaten die eine Zwangsbedingung falsch ist, ist damit leider immer noch nicht geklärt... |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 22. Jul 2012 10:14 Titel: franz Verfasst am: 22. Jul 2012 10:14 Titel: |
 |
|
Kannst Du Deine Rechnung dazu mal kurz aufschreiben?
 ist in Kugelkoordianten schlicht nur die Umrechnung zu kartesischen, z = Höhe quasi. ist in Kugelkoordianten schlicht nur die Umrechnung zu kartesischen, z = Höhe quasi. |
|
 |
Rmn
Anmeldungsdatum: 26.01.2010
Beiträge: 473
|
 Rmn Verfasst am: 22. Jul 2012 10:18 Titel: Rmn Verfasst am: 22. Jul 2012 10:18 Titel: |
 |
|
Sie ist nicht falsch, für für z>0

sind beide Bedingungen äquivalent.
In kartesischen Koordinaten rechnest du dich tot mit Wurzeln. In Zylinderkoordinaten sehen Bewegnungsgleichungen anders aus, da muss du sie nachschauen. |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 22. Jul 2012 10:25 Titel: franz Verfasst am: 22. Jul 2012 10:25 Titel: |
 |
|
 |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 22. Jul 2012 10:42 Titel: Nima93 Verfasst am: 22. Jul 2012 10:42 Titel: |
 |
|
Super, danke! Das heißt für fast alle Winkel ist es egal, welche der Zwangsbedingungen ich nehme? Aber es muss doch eine Möglichkeit geben, vorher zu sehen, ob die Zwangsbedingung für alle Winkel funktioniert? In meinem Fall war ja das Problem, dass die Bewegungsgleichungen für Theta = pi/2 gelöst werden sollte. Der Tangens ist für diesen Winkel ja leider nicht definiert  |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 22. Jul 2012 12:31 Titel: franz Verfasst am: 22. Jul 2012 12:31 Titel: |
 |
|
|
Den Tangens brauchst Du doch garnicht, siehe oben. Und in der Bewegungsgleichung verschwindet dann der Rotationsterm. |
|
 |
Rmn
Anmeldungsdatum: 26.01.2010
Beiträge: 473
|
 Rmn Verfasst am: 22. Jul 2012 19:44 Titel: Rmn Verfasst am: 22. Jul 2012 19:44 Titel: |
 |
|
Deine Zwangsbedingung resultiert aus der geometrischen Überlegung 
für  gilt offensichtlich z=0, damit würdest du durch Null teilen; deswegen existiert auch Tangens nicht. Das siehst man ohne zu rechnen, spätenstens, wenn man eine Skizze macht. gilt offensichtlich z=0, damit würdest du durch Null teilen; deswegen existiert auch Tangens nicht. Das siehst man ohne zu rechnen, spätenstens, wenn man eine Skizze macht. |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 28. Jul 2012 14:25 Titel: Nima93 Verfasst am: 28. Jul 2012 14:25 Titel: |
 |
|
Alles klar, danke, eigentlich logisch  |
|
 |
|
















 Wahrscheinlich steh ich wieder mal völlig auf dem Schlauch... könnte mir jemand mal kurz erklären, was ich dann anders machen muss, als in kartesischen Koordinaten? Klar, ich muss die Formel für die Geschwindikeit in Zylinderkoordinaten in die Bewegungsgleichung einsetzen. Aber wie rechne ich die Zwangskräfte aus?
Wahrscheinlich steh ich wieder mal völlig auf dem Schlauch... könnte mir jemand mal kurz erklären, was ich dann anders machen muss, als in kartesischen Koordinaten? Klar, ich muss die Formel für die Geschwindikeit in Zylinderkoordinaten in die Bewegungsgleichung einsetzen. Aber wie rechne ich die Zwangskräfte aus?
