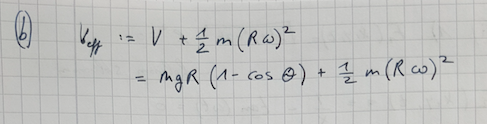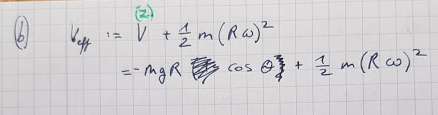| Autor |
Nachricht |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 19. Dez 2016 21:33 Titel: Lagrange Mechanik - Perle auf Ring |
 |
|
Hi,
kann mir vlt. jemand sagen wieso in der Aufgabe bei a) (iii) für das Potential
mg*(-Rcos(theta)) angesetzt wird und nicht
mg*(R-Rcos(theta))?
Und wie geht man bei der b) vor um auf V_eff zu kommen? Aus der Gleichung, die angegeben ist ergibt sich V_eff=T_eff-L, aber woher bekomme ich T_eff? Ich habe lediglich L und T..
Danke!
| Beschreibung: |
|
| Dateigröße: |
221.29 KB |
| Angeschaut: |
5160 mal |
|
|
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 19. Dez 2016 21:36 Titel: Re: Lagrange Mechanik - Perle auf Ring |
|
|
| Amateurphysiker hat Folgendes geschrieben: |
kann mir vlt. jemand sagen wieso in der Aufgabe bei a) (iii) für das Potential
mg*(-Rcos(theta)) angesetzt wird und nicht
mg*(R-Rcos(theta))?
|
Was ist denn der Unterschied?
| Zitat: |
Und wie geht man bei der b) vor um auf V_eff zu kommen? Aus der Gleichung, die angegeben ist ergibt sich V_eff=T_eff-L, aber woher bekomme ich T_eff? Ich habe lediglich L und T..
|
Wie ist denn V_eff?
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 19. Dez 2016 21:46 Titel: Re: Lagrange Mechanik - Perle auf Ring |
|
|
| jh8979 hat Folgendes geschrieben: |
Was ist denn der Unterschied?
|
Achso, bei ersterem ist das Potential auf Z=R gleich 0 gesetzt, bei letzterem bei Z=0?
| jh8979 hat Folgendes geschrieben: |
Wie ist denn V_eff? |
So? https://de.wikipedia.org/wiki/Effektives_Potential
Was soll dann die Gleichung in der Aufgabenstellung? L(θ, θ ̇) = Teff(θ ̇) − Veff(θ)
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 19. Dez 2016 21:57 Titel: Re: Lagrange Mechanik - Perle auf Ring |
|
|
| Amateurphysiker hat Folgendes geschrieben: | | jh8979 hat Folgendes geschrieben: |
Was ist denn der Unterschied?
|
Achso, bei ersterem ist das Potential auf Z=R gleich 0 gesetzt, bei letzterem bei Z=0?
|
Da steht doch gar kein Z...
Keine Ahnung was die soll... weiss ja nicht was ihr in der Vorlesung gemacht habt. Man darf Hinweise in Aufgabenstellungen aber auch ignorieren, wenn man anders zum Ziel kommt.
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 20. Dez 2016 13:43 Titel: Re: Lagrange Mechanik - Perle auf Ring |
|
|
| jh8979 hat Folgendes geschrieben: |
Da steht doch gar kein Z...
|
g wirkt doch entlang der z-Achse, entsprechend ist doch das potential eine funktion von z oder nicht?
| jh8979 hat Folgendes geschrieben: |
Keine Ahnung was die soll... weiss ja nicht was ihr in der Vorlesung gemacht habt. Man darf Hinweise in Aufgabenstellungen aber auch ignorieren, wenn man anders zum Ziel kommt. |
Also stimmt es so (siehe anhang)?
| Beschreibung: |
|
| Dateigröße: |
102.93 KB |
| Angeschaut: |
5492 mal |
|
|
|
|
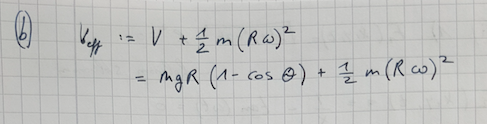
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 20. Dez 2016 16:06 Titel: Re: Lagrange Mechanik - Perle auf Ring |
|
|
| Amateurphysiker hat Folgendes geschrieben: | | jh8979 hat Folgendes geschrieben: |
Da steht doch gar kein Z...
|
g wirkt doch entlang der z-Achse, entsprechend ist doch das potential eine funktion von z oder nicht?
|
Ich seh da kein z in Deiner Formel.
| Zitat: |
Also stimmt es so (siehe anhang)? |
Sieht halbwegs richtig aus... aber die Vorzeichen wuerde ich nochmal überprüfen.
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 20. Dez 2016 16:40 Titel: Re: Lagrange Mechanik - Perle auf Ring |
|
|
| jh8979 hat Folgendes geschrieben: |
Ich seh da kein z in Deiner Formel.
|
Ok^^
| jh8979 hat Folgendes geschrieben: |
Sieht halbwegs richtig aus... aber die Vorzeichen wuerde ich nochmal überprüfen. |
Ok das V muss Minus sein. Aber den zweiten Term - also den azimutalen Anteil der kinetischen Energie - habe ich von hier mit Plus übernommen, stimmt das nicht? https://de.wikipedia.org/wiki/Effektives_Potential
Danke!
| Beschreibung: |
|
| Dateigröße: |
64.22 KB |
| Angeschaut: |
5478 mal |
|
|
|
|
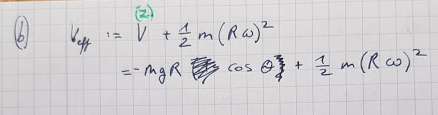
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 20. Dez 2016 16:52 Titel: |
|
|
|
L = T - V
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 20. Dez 2016 17:56 Titel: |
|
|
Was hat das mit V_eff zu tun?
V_eff=V+T_azimutal oder?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 20. Dez 2016 20:32 Titel: |
|
|
| Amateurphysiker hat Folgendes geschrieben: | Was hat das mit V_eff zu tun?
|
Denk mal drüber nach. Gilt auch für T_eff und V_eff (wie auf dem Aufgabenzettel steht).
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 20. Dez 2016 21:20 Titel: |
|
|
Ok aber das führt mich dann wieder zu meiner Ausgangsfrage, wie ist denn T_eff überhaupt definiert? Ich finde da leider überhaupt nichts dazu... Die Gleichung bringt mir ja nichts, wenn ich zwei Unbekannte darin habe..
Was ist denn an der Gleichung hier falsch, bzw. wieso kann ich sie nicht anwenden? https://de.wikipedia.org/wiki/Effektives_Potential
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 20. Dez 2016 21:27 Titel: |
|
|
| Amateurphysiker hat Folgendes geschrieben: | Ok aber das führt mich dann wieder zu meiner Ausgangsfrage, wie ist denn T_eff überhaupt definiert? Ich finde da leider überhaupt nichts dazu... Die Gleichung bringt mir ja nichts, wenn ich zwei Unbekannte darin habe..
Was ist denn an der Gleichung hier falsch, bzw. wieso kann ich sie nicht anwenden? https://de.wikipedia.org/wiki/Effektives_Potential |
Du kannst Sie anwenden, Deine Vorzeichen sind nur falsch.
Der Punkt beim effektiven Potential ist, dass die Bewegungsgleichung dann genauso aussieht wie bei einer normalen eindimensionalen Bewegung, aber mit Veff statt V. Das heisst man kann alles, was man über das Lösen von Bewegungen in einem eindimensionalen Potential weiss, benutzen.
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 21. Dez 2016 11:40 Titel: |
|
|
Hmm.. kannst du mir sagen wieso aus Zeile 1 und 2, Zeilen 3 und 4 folgen (Anhang)? Die Logik kann ich nicht nachvollziehen..Danke!
| Beschreibung: |
|
| Dateigröße: |
143.61 KB |
| Angeschaut: |
5146 mal |
|
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 21. Dez 2016 17:03 Titel: |
|
|
|
Alles mit Ableitungen ist Teff, der Rest Veff.
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 08. März 2017 18:04 Titel: |
|
|
Ich versteh nicht was du meinst!
Wie wurde hier (3) bestimmt?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 08. März 2017 19:06 Titel: |
|
|
|
Alle Terme die Ableitungen enthalten gehören zur effektiven kinetischen Energie T_eff (denn wenn die Ableitung Null sind, bewegt sich nichts und die kinetische Energie ist Null). Der Rest gehört dann zum effektiven Potential V_eff.
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 09. März 2017 16:08 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | Alle Terme die Ableitungen enthalten gehören zur effektiven kinetischen Energie T_eff |
Was soll das bedeuten? Kinetische Energie ist doch per Definition 1/2mv^2, wobei v die Ableitung des Ortsvektors ist. In wie fern unterscheidet sich die effektive kinE von der "normalen" kE?
edit: sorry, ich hab es verstanden glaub ich!!
danke!!
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 09. März 2017 16:16 Titel: |
|
|
bzw. teilweise verstanden! :-)
in dem tangentialteil der KE steht ja noch ein omega, was ja ableitung von phi ist und somit auch bewegungsabhängig ist. Wieso zählt der Term dan nicht zur eff. KE?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 09. März 2017 16:17 Titel: |
|
|
| Amateurphysiker hat Folgendes geschrieben: |
Was soll das bedeuten? Kinetische Energie ist doch per Definition 1/2mv^2, wobei v die Ableitung des Ortsvektors ist. In wie fern unterscheidet sich die effektive kinE von der "normalen" kE?
edit: sorry, ich hab es verstanden glaub ich!!
danke!! |
Dann erklär es uns doch mal 
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 09. März 2017 17:07 Titel: |
|
|
Haha ok! :-)
Die effektive kinetische Energie enthält nur den bewegungsabhängigen Anteil der gesamten KE, wobei der Lage-abhänge Anteil dem effektiven Potential zugerechnet wird.
Wie gesagt hier nur meine Frage, wieso der Term mit Omega dann als nicht bewegungsabhängig betrachtet wird?
Irgendwo scheint mein Verständnis noch nicht ganz aufzugehen..
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 13. März 2017 15:22 Titel: |
|
|
Stimmt das? Bzw. wo ist mein Denkfehler?
Danke!
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 13. März 2017 21:31 Titel: |
|
|
|
Wenn Du Deine generalisierte Koordinate einfach mal x nennst, siehst Du vielleicht besser wieso man von effektiver kinetischer Energie und effektivem Potential spricht.
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 21. März 2017 17:08 Titel: |
|
|
Ich verstehe nicht. Wir haben doch zwei gen. Koordinaten? Theta und Phi.
Der "nicht-effektive" Anteil der KE hängt zwar nicht von Theta Punkt ab, aber doch immer noch von Phi Punkt. Weshalb wird er also nicht zur effektiven KE gerechnet?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 21. März 2017 21:50 Titel: |
|
|
| Amateurphysiker hat Folgendes geschrieben: | | Ich verstehe nicht. Wir haben doch zwei gen. Koordinaten? Theta und Phi. |
Nein, es gibt nur eine.
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 27. März 2017 14:29 Titel: |
|
|
Ah ok stimmt!
Wäre es dann richtig zu sagen: Das effektive Potential enthält den Anteil der kinetischen Energie, der nicht von der/den generalisierten Geschwindigkeit(en) abhängt?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 27. März 2017 15:05 Titel: |
|
|
| Amateurphysiker hat Folgendes geschrieben: | Ah ok stimmt!
Wäre es dann richtig zu sagen: Das effektive Potential enthält den Anteil der kinetischen Energie, der nicht von der/den generalisierten Geschwindigkeit(en) abhängt? |
In der Regel schon. Man könnte mir aber durchaus Fälle vorstellen, in denen ein geschwindigkeitsabhängiges (generalisierten) Potential existiert.
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
| Amateurphysiker Verfasst am: 27. März 2017 17:36 Titel: |
|
|
|
Ok, aber was ist denn die allgemeine Definition des effektiven Potentials?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 27. März 2017 17:43 Titel: |
|
|
|
Es handelt sich um einen Anteil der kinetischen Energie, der aufgrund der Existenz von Erhaltungsgrößen so umgeschrieben werden kann, dass keine (verallgemeinerten) Geschwindigkeiten mehr auftreten.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 27. März 2017 18:01 Titel: |
|
|
| Amateurphysiker hat Folgendes geschrieben: | | Ok, aber was ist denn die allgemeine Definition des effektiven Potentials? |
Der Punkt ist doch, dass man danach Teff und Veff hat und beide formal so sind, wie man es von normalem T und V in der Mechanik kennt. Dann kann man alles was man in der Mechanik über Bewegungen in einem Potential gelernt hat einfach anwenden ohne es nochmal herleiten zu müssen (und fast immer ist das Potential gescheindigkeitsunabhaengig, falls dich der Teil meiner Antwort verwirrt hat).
|
|
|
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
|
|
|
Registrieren
Login
FAQ
Suchen
