| Autor |
Nachricht |
juliet4815
Anmeldungsdatum: 31.01.2022
Beiträge: 26
|
 juliet4815 Verfasst am: 05. Jun 2022 00:02 Titel: Zwangsbedingung Massen auf schiefer Ebene juliet4815 Verfasst am: 05. Jun 2022 00:02 Titel: Zwangsbedingung Massen auf schiefer Ebene |
 |
|
Meine Frage:
Auf einer schiefen Ebene sind zwei durch ein Seil verbundene Massenpunkte wie in der Skizze dargestellt platziert. Das Seil hat eine konstante Länge l und die Bewegungen der Massenpunkte erfolgt vollkommen reibungsfrei.
Welche Zwangsbedingungen gibt es? Drücke die kartesischen Koordinaten (x1, y1) und (x2, y2) durch generalisierte Koordinaten aus.
Meine Ideen:
Ich finde es generell leider recht schwierig auszumachen, was genau Zwangsbedingungen in einem System darstellen und wie man am besten die generalisierten Koordinaten formuliert (also auch falls jemand unabhängig von der Aufgabe einen guten Tipp hat, freue ich mich)
Also zumindest sollten z1=0 und z2=0 schonmal zwei Zwangsbedingung sein und dann wird es schon kritisch ...
Ich dachte, vielleicht kann man die Längen mit Hilfe des Winkels ausdrücken z.B.
=\frac{h}{L_{1}}, \sin(\beta )=\frac{h}{L_{2}} ) mit der Höhe h und somit mit der Höhe h und somit
*L_{1}=\sin(\beta)*L_{2} ) , aber was mir das jetzt wirklich bringen soll, weiß ich leider nicht, es muss ja sicher auch noch einen Zusammenhang mit den Seillängen geben, nur , aber was mir das jetzt wirklich bringen soll, weiß ich leider nicht, es muss ja sicher auch noch einen Zusammenhang mit den Seillängen geben, nur
 sollte nicht allgemein gelten oder? sollte nicht allgemein gelten oder?
Wenn ich jetzt meine Zwangsbedingungen kennen würde, könnte ich mir ja überlegen:
Es gibt 3*n Freiheitsgrade, hier haben wir 2 Massen also 6 Freiheitsgrade. Von diesen ziehe ich die Anzahl der Zwangsbedingungen ab, dann ergibt sich die Anzahl der generalisierten Koordinaten. Ich würde mal vermuten, es gibt 4 Zwangsbedingungen und man bräuchte schließlich zwei generalisierte Koordinaten. Das wäre auch mit der Aufgabenstellung konsistent, da dort von (x1, y1) und (x2, y2) gesprochen wird, oder?
Bezüglich dessen, wie ich diese nun aufstelle, bin ich in diesem Fall leider verwirrt.
Vielen Dank schonmal für die Hilfe :)
| Beschreibung: |
|

Download |
| Dateiname: |
Bildschirmfoto 2022-06-05 um 00.04.14.png |
| Dateigröße: |
34.18 KB |
| Heruntergeladen: |
154 mal |
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 05. Jun 2022 09:40 Titel: Huggy Verfasst am: 05. Jun 2022 09:40 Titel: |
 |
|
Generalisierte Koordinaten sind Größen, die ausreichend sind, die Positionen aller beteiligten Körper (hier die beiden Massen 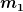 und und 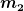 ) eindeutig zu bestimmen. Wenn sich die beiden Massen auf den beiden schiefen Ebenen befinden sollen (die Zwangsbedingungen), genügen dazu die beiden Seillängen ) eindeutig zu bestimmen. Wenn sich die beiden Massen auf den beiden schiefen Ebenen befinden sollen (die Zwangsbedingungen), genügen dazu die beiden Seillängen 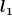 und und  . Und da die gesamte Seillänge . Und da die gesamte Seillänge  konstant sein soll, genügt sogar eine der beiden Teillängen. Man kann also z. B. konstant sein soll, genügt sogar eine der beiden Teillängen. Man kann also z. B. 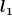 als generalisierte Koordinate nehmen. als generalisierte Koordinate nehmen.
Da es sich um ein ebenes Problem handelt, hat man nur  Freiheitsgrade, nämlich die Freiheitsgrade, nämlich die ) -Koordinaten der beiden Massen. Es dürfte bequem sein, den Ursprung des Koordinatensystems in die obere Ecke des Dreiecks zu legen. -Koordinaten der beiden Massen. Es dürfte bequem sein, den Ursprung des Koordinatensystems in die obere Ecke des Dreiecks zu legen.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 05. Jun 2022 10:29 Titel: TomS Verfasst am: 05. Jun 2022 10:29 Titel: |
 |
|
Generalisierte Koordinaten sind unabhängige Größen, die das System im jeweiligen Konfigurationsraum beschreiben.
In deinem Fall ist der Anschauungsraum der 3-dim. Raum. Da zwei Teilchen im 3-dim. Anschauungsraum vorliegen, verwendet man zunächst den 6-dim. Konfigurationsraum mit den 6-Tupeln
)
Nun liegen zwei Gruppen von Zwangsbedingungen vor:
1) die Teilchen befinden sich auf einer schiefen Ebene
2) die Teilchen sind durch ein Seil verbunden
Diese Zwangsbedingungen reduzieren die Anzahl der unabhängigen Koordinaten, d.h. die Dimension des Konfigurationsraumes.
1) da die 2 Teilchen sich auf einer 2-dim. Ebene bewegen, werden nur 2 * 2 Koordinaten benötigt; d.h. der 6-dim. Konfigurationsraum kann durch Finden geeigneter Koordinaten auf 4 Dimensionen reduziert werden
2) da die Teilchen durch ein Seil verbunden sind, fällt eine weitere Dimension weg
Es gibt zwei Möglichkeiten, Zwangsbedingungen zu lösen
a) explizit durch das Finden geeigneter generalisierte Koordinaten im Konfigurationsraum, die die Zwangsbedingungen lösen
b) implizit durch Verwendung „zu vieler“ generalisierte Koordinaten plus das Einführen der Zwangsbedingungen mittels Lagrange-Multiplikatoren
Beides kann auch kombiniert werden.
Ich würde mir an deiner Stelle noch ein anderes System ansehen, nämlich zwei durch eine masselose Stange fester Länge verbundener Teilchen auf einer unendlich ausgedehnten schiefen Ebene. Daraus lernt man m.E. viel mehr.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 05. Jun 2022 12:24, insgesamt einmal bearbeitet |
|
 |
juliet4815
Anmeldungsdatum: 31.01.2022
Beiträge: 26
|
 juliet4815 Verfasst am: 05. Jun 2022 11:28 Titel: juliet4815 Verfasst am: 05. Jun 2022 11:28 Titel: |
 |
|
Ok schonmal vielen Dank für die Mühe.
Zu 1) Die Dimension in z-Richtung ist ja schonmal weggefallen, dann bleibt noch x und y. Dafür könnte man ja =\frac{y_{1}}{x_{1}}, \tan(\beta)=-\frac{y_{2}}{x_{2}} )
verwenden und zu 2) wie schon angesprochen 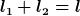
Dann bleibt nur noch eine generalisierte Koordinate übrig, bei einer normalen schiefen Ebene benutzt man dafür ja nun r bzw. s, also die "Wegstrecke", die die Masse rutscht. Eine andere Möglichkeit bleibt ja auch eigentlich hier nicht, die Winkel sind nicht veränderlich und die Länge der Seilteilstücke hängen direkt mit dem zurückgelegten Weg zusammen.
Dafür hätte ich nun Polarkoordinaten gewählt, für m1 würde das auch so funktionieren:
, y_{1}=s_{1}*\sin(\alpha ) )
Dann hätte ich den Ursprung nur nicht, wie ihr geraten habt, in der Spitze des Dreiecks, sondern der linken Ecke.
Daher stellt sich nun jedoch auch das Problem für die zweite Masse ...
Bei dieser hängt die Weglänge ja nun direkt mit der Länge des Seils und der zurückgelegten Wegstrecke von Masse 1 zusammen, da sie über das Seil verbunden sind
 ) sollte sich ja nun hier für s2 ergeben ... jetzt könnte man wieder Polarkoordinaten verwenden, nur wie mache ich das, wenn der Winkel genau in die andere Richtung zeigt ... sollte sich ja nun hier für s2 ergeben ... jetzt könnte man wieder Polarkoordinaten verwenden, nur wie mache ich das, wenn der Winkel genau in die andere Richtung zeigt ...
Ich hoffe, ich kam auf ein paar brauchbare Ansätze, würde mich freuen, wenn ihr mir noch einen Tipp geben könnt, wie man die Ausrichtung des Koordinatensystems dann zu verstehen hat. Bei einem der beiden (also x1 oder x2 muss dann ja auch noch sicher ein Minus dazu)
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 05. Jun 2022 12:20 Titel: TomS Verfasst am: 05. Jun 2022 12:20 Titel: |
 |
|
Einschub -
Ich skizziere mal diesen Fall zweier durch eine masselose Stange fester Länge l verbundener Teilchen auf einer unendlich ausgedehnten schiefen Ebene mit Neigungswinkel alpha, da man hier eine Vielzahl möglicher Variablen zu (1, 2) sowie (a, b) diskutieren kann.
Ich lasse Vektorpfeile grundsätzlich weg, r steht immer für einen Vektor bzw. das entsprechende 3-Tupel
; \; a=1 \ldots 2)
1) Zunächst im 6-dim. Konfigurationsraum, wobei die Ebene um den Winkel alpha um die y-Achse rotiert ist.
)

^2 - l^2 = 0)
Die erste Zwangsbedingung kann man im Sinne von (a) explizit einsetzen oder im Sinne von (b) indirekt implementieren; (a) ist sicher sinnvoll. Die zweite Zwangsbedingung wird man zunächst implizit im Sinne von (b) implementieren.
2) Allerdings kann man beide Zwangsbedingung gemeinsam explizit verwenden. Dazu betrachtet man jedoch völlig andere Koordinaten.
Zunächst definiert man auf der xy-Ebene d.h. für z = 0 im 3-dim Raum die Koordinaten
)
Ausgehend von diesem Punkt eta definiert man zwei Punkte
 = (\xi \pm \lambda\,\cos\phi, y \pm \lambda\,\sin\phi, 0) )
d.h. sie liegen auf einem Kreis mit Radius

und parametrisiert durch den Winkel phi um den zunächst definierten Punkt eta, der bei identischen Massen zugleich Mittelpunkt der Stange und Massenmittelpunkt ist.
Nun rotiert man diese Ebene um den Winkel alpha um die y-Achse, d.h. man führt eine entsprechende Rotationsmatrix ein und schreibt

Die neuen verallgemeinerten Koordinaten, die die Zwangsbedingungen explizit lösen, lauten demnach
 )
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 05. Jun 2022 12:26, insgesamt einmal bearbeitet |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 05. Jun 2022 12:24 Titel: Huggy Verfasst am: 05. Jun 2022 12:24 Titel: |
 |
|
Was willst du mit Polarkoordinaten? Ich bleibe mal bei meinem Vorschlag, ein kartesisches Koordinatensystem zu verwenden mit dem Ursprung in der oberen Ecke des Dreiecks und der positiven x-Achse nach rechts und der positiven y-Achse nach oben. Dann hat man simpel
=l_1 (- \cos \alpha, - \sin \alpha))
=l_2 ( \cos \beta, - \sin \beta)=(l-l_1)( \cos \beta, - \sin \beta))
Du kannst gern davon abweichen. Viele Wege führen nach Rom.
|
|
 |
juliet4815
Anmeldungsdatum: 31.01.2022
Beiträge: 26
|
 juliet4815 Verfasst am: 05. Jun 2022 12:40 Titel: juliet4815 Verfasst am: 05. Jun 2022 12:40 Titel: |
 |
|
Mhh, ich dachte wohl, ich hätte Polarkoordinaten verwendet, bzw. hatte es vor, aber habe eigentlich doch kartesische benutzt.
Ich habe es mir eben nochmal aufgezeichnet und es ergibt für mich jetzt auch Sinn, nur die Vorzeichen verstehe ich noch nicht so ganz, wenn ihr mir noch dabei helfen könntet, würde ich mich sehr freuen :)
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 05. Jun 2022 12:47 Titel: Huggy Verfasst am: 05. Jun 2022 12:47 Titel: |
 |
|
Die Vorzeichen ergeben sich aus der Orientierung der Achsen und der Wahl des Koordinatenursprungs. Die y-Koordinaten beider Massen liegen unterhalb des gewählten Koordinatenursprungs, müssen also negativ sein. 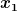 liegt links vom gewählten Koordinatenursprung, muss also negativ sein. liegt links vom gewählten Koordinatenursprung, muss also negativ sein.  liegt rechts davon, muss also positiv sein. liegt rechts davon, muss also positiv sein.
|
|
 |
juliet4815
Anmeldungsdatum: 31.01.2022
Beiträge: 26
|
 juliet4815 Verfasst am: 05. Jun 2022 12:49 Titel: juliet4815 Verfasst am: 05. Jun 2022 12:49 Titel: |
 |
|
|
Ahhhh, ja das ergibt doch Sinn, vielen lieben Dank euch beiden! :)
|
|
 |
jmd
Anmeldungsdatum: 28.10.2012
Beiträge: 577
|
 jmd Verfasst am: 05. Jun 2022 15:04 Titel: jmd Verfasst am: 05. Jun 2022 15:04 Titel: |
 |
|
Zusammenfassend die 3 Zwangsbedingungen
 )
-y_1\cos(\alpha ) =0 )
 )
+y_2\cos(\alpha )=0 )
 } +\frac{x_2}{\cos(\beta ) } )
 } +\frac{x_2}{\cos(\beta ) }-l =0 )
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 05. Jun 2022 16:31 Titel: Zwangsbedingungen roycy Verfasst am: 05. Jun 2022 16:31 Titel: Zwangsbedingungen |
 |
|
| TomS hat Folgendes geschrieben: |
Diese Zwangsbedingungen reduzieren die Anzahl der unabhängigen Koordinaten, d.h. die Dimension des Konfigurationsraumes.
Es gibt zwei Möglichkeiten, Zwangsbedingungen zu lösen
a) explizit durch das Finden geeigneter generalisierte Koordinaten im Konfigurationsraum, die die Zwangsbedingungen lösen
b) implizit durch Verwendung „zu vieler“ generalisierte Koordinaten plus das Einführen der Zwangsbedingungen mittels Lagrange-Multiplikatoren
Beides kann auch kombiniert werden.
Ich würde mir an deiner Stelle noch ein anderes System ansehen, nämlich zwei durch eine masselose Stange fester Länge verbundener Teilchen auf einer unendlich ausgedehnten schiefen Ebene. Daraus lernt man m.E. viel mehr. |
Jetzt dreht mal nicht durch;-)
|
|
 |
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 05. Jun 2022 21:21 Titel: Re: Zwangsbedingung Massen auf schiefer Ebene roycy Verfasst am: 05. Jun 2022 21:21 Titel: Re: Zwangsbedingung Massen auf schiefer Ebene |
 |
|
| juliet4815 hat Folgendes geschrieben: | Meine Frage:
Auf einer schiefen Ebene sind zwei durch ein Seil verbundene Massenpunkte wie in der Skizze dargestellt platziert. Das Seil hat eine konstante Länge l und die Bewegungen der Massenpunkte erfolgt vollkommen reibungsfrei.
Welche Zwangsbedingungen gibt es? Drücke die kartesischen Koordinaten (x1, y1) und (x2, y2) durch generalisierte Koordinaten aus.
Meine Ideen:
Ich finde es generell leider recht schwierig auszumachen, was genau Zwangsbedingungen in einem System darstellen und wie man am besten die generalisierten Koordinaten formuliert (also auch falls jemand unabhängig von der Aufgabe einen guten Tipp hat, freue ich mich)
Also zumindest sollten z1=0 und z2=0 schonmal zwei Zwangsbedingung sein und dann wird es schon kritisch ...
Ich dachte, vielleicht kann man die Längen mit Hilfe des Winkels ausdrücken z.B.
=\frac{h}{L_{1}}, \sin(\beta )=\frac{h}{L_{2}} ) mit der Höhe h und somit mit der Höhe h und somit
*L_{1}=\sin(\beta)*L_{2} ) , aber was mir das jetzt wirklich bringen soll, weiß ich leider nicht, es muss ja sicher auch noch einen Zusammenhang mit den Seillängen geben, nur , aber was mir das jetzt wirklich bringen soll, weiß ich leider nicht, es muss ja sicher auch noch einen Zusammenhang mit den Seillängen geben, nur
 sollte nicht allgemein gelten oder? sollte nicht allgemein gelten oder?
Wenn ich jetzt meine Zwangsbedingungen kennen würde, könnte ich mir ja überlegen:
Es gibt 3*n Freiheitsgrade, hier haben wir 2 Massen also 6 Freiheitsgrade. Von diesen ziehe ich die Anzahl der Zwangsbedingungen ab, dann ergibt sich die Anzahl der generalisierten Koordinaten. Ich würde mal vermuten, es gibt 4 Zwangsbedingungen und man bräuchte schließlich zwei generalisierte Koordinaten. Das wäre auch mit der Aufgabenstellung konsistent, da dort von (x1, y1) und (x2, y2) gesprochen wird, oder?
Bezüglich dessen, wie ich diese nun aufstelle, bin ich in diesem Fall leider verwirrt.
Vielen Dank schonmal für die Hilfe  |
Was soll denn eigentlich geschehen?
Ist ein Gleichgewichtszustand gesucht oder die Beschleunigung? Welche Masse ist größer (sofern überhauß)t? In welche Richtung hin soll eine evtl. Bewegung erfolgen?
|
|
 |
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
 vtxt1103 Verfasst am: 05. Jun 2022 21:23 Titel: vtxt1103 Verfasst am: 05. Jun 2022 21:23 Titel: |
 |
|
|
Mich wundert übringens auch dass in der Aufgabenstellung von mehreren generealisierTEN KoordinaTEN gesprochen wird, man braucht eigentlich nur l1 als generealisierte Koordinate
|
|
 |
|
|
















