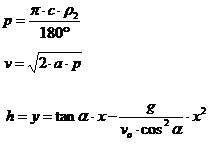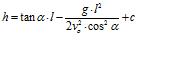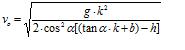| Autor |
Nachricht |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 30. Okt 2008 17:52 Titel: Schiefer Wurf mit Katapult Simo86 Verfasst am: 30. Okt 2008 17:52 Titel: Schiefer Wurf mit Katapult |
 |
|
Aufgabe: Ein Katapult mit der Länge l=5m dass schon im Winkel von alpha=5° ausgelenkt ist. Beim loslassen des Katapults schlägt es auf Alpha= 55° aus und man muss die Winkelgeschwindigkeit berechnen so dass die Kugel eine Mauer die 50 m entfernt ist in der Höhe von h= 7m treffen.
Wie ermittle ich die Winkelgeschwindigkeit.
Also ich denke das ich eine Anfangsgeschwindigkeit ermitteln muss die so groß sein mein muss dass die Kugel die Wand in 7 m Höhe erreichen muss mit berücksichtigug der Anziehungskraft:
x(t)=h-vo*t+0.5gt^2
t= sprt((2h)/g)
doch wie beachte ich den Winkel mit????
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Okt 2008 18:20 Titel: dermarkus Verfasst am: 30. Okt 2008 18:20 Titel: |
 |
|
* Magst du nochmal schauen, ob du die Aufgabenstellung hier auch wirklich wörtlich wiedergegeben hast? Welche Winkelgeschwindigkeit ist hier genau gesucht?
* Für die Flugphase hast du bisher nur eine Gleichung für die vertikale Bewegung sowie eine Gleichung für ein t (was genau soll dieses t sein, und für welchen Spezialfall ist es gemeint?) hingeschrieben. Nun ist aber sicher auch die horizontale Komponente der Flugbewegung wichtig. Kannst du die auch noch mit berücksichtigen, oder kennst du vielleicht schon direkt eine Gleichung für die Wurfparabel, so dass du direkt mit der arbeiten könntest?
Hilft es dir, vielleicht mal eine Skizze von der ganzen Anordnung zu machen?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 30. Okt 2008 18:31 Titel: Simo86 Verfasst am: 30. Okt 2008 18:31 Titel: |
 |
|
Echter Text:
Die Belagerer einer Burg versuchen die Burgmauer mit einem Katapult zu zerstören. Das Katapult steht auf einer Ebene 0 m von der Burgmauer entfernt. Der Arm des Katapults besitzt eine Länge von 5m und der Winkel, unter den das Geschoss abgeschossen wird, beträgt α1=55°. Mit welcher Winkelbeschleunigung muss das geschoss beschleunigt werden um die Burgmauer in Höhe von 7m zu treffen, wenn das geladene Katapult mit α0=5° ausgelenkt ist.
An der Formel bin ich am basteln.. ist ganz schön schwierig da man x und y richtung berücksichtung muss...
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Okt 2008 18:41 Titel: dermarkus Verfasst am: 30. Okt 2008 18:41 Titel: |
 |
|
|
Ah, okay, dann ist am Ende sogar die Winkelbeschleunigung gefragt, und nicht eine Winkelgeschwindigkeit, die höchstens ein Zwischenergebnis sein wird.
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 30. Okt 2008 20:59 Titel: Sonex Verfasst am: 30. Okt 2008 20:59 Titel: |
 |
|
Also komme da nicht ganz klar.
bis jetzt:
Geschosshöhe: h=ho+vo sinα t +g/2 t^2
Geschossweite: x=vo cosα t
Flugdauer: t= (vo sinα / g ) + wurzel ( ((vo sinα)/g)^2 + (2ho/g))
jedoch wie berücksichte ich die 5 m Katapultlänge sowie die Winkeldifferenz. und die wichtige Frage wie aus den Formel eine Winkelbeschleunigung raus kommen soll?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Okt 2008 21:08 Titel: dermarkus Verfasst am: 30. Okt 2008 21:08 Titel: |
 |
|
Magst du dir am besten für das ganze mal eine Skizze machen? (Und diese Skizze, wenn du magst, gerne mal hier zeigen.)
| Sonex hat Folgendes geschrieben: |
Geschosshöhe: h=ho+vo sinα t +g/2 t^2
Geschossweite: x=vo cosα t
|
Das sieht soweit schon mal ganz okay aus. Wie meinst du dabei das Vorzeichen von 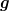 bzw. das Vorzeichen des quadratischen Terms in deiner Gleichung für die Geschosshöhe bzw. das Vorzeichen des quadratischen Terms in deiner Gleichung für die Geschosshöhe ) ? ?
| Zitat: |
Flugdauer: t= (vo sinα / g ) + wurzel ( ((vo sinα)/g)^2 + (2ho/g))
|
Wie hast du diese Gleichung aufgestellt? Gilt diese Gleichung für einen Flug, wie ihn deine Skizze für diese Aufgabe zeigt, oder war diese Gleichung für einen anderen Fall aufgestellt worden? Wo endet der Flug in dieser Aufgabe, wo endet der Flug in dem Fall, der für das Aufstellen dieser Gleichung für  genommen wurde? genommen wurde?
| Zitat: |
jedoch wie berücksichte ich die 5 m Katapultlänge sowie die Winkeldifferenz. und die wichtige Frage wie aus den Formel eine Winkelbeschleunigung raus kommen soll? |
Wenn du magst, könntest du da zum Beispiel schon mal Gleichungen aufstellen, die sagen, wie diese Winkelgrößen mit der Abwurfgeschwindigkeit 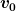 zusammenhängen. zusammenhängen.
Dann kannst du am Ende, wenn du mit Hilfe der "Flugbetrachtungen" herausbekommen hast, wie groß das 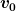 ist, daraus die gefragten Winkelgrößen ausrechnen. ist, daraus die gefragten Winkelgrößen ausrechnen.
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 30. Okt 2008 21:28 Titel: Simo86 Verfasst am: 30. Okt 2008 21:28 Titel: |
 |
|
|
Muss ich meine gleichung so aufbauen das vo abhängig ist von der Katapult länge. denn je länger der katapult ist unter dem gleichen winkel desto länger ist doch der beschleunigungsweg. oder ist die richtung verkehrt.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Okt 2008 21:34 Titel: dermarkus Verfasst am: 30. Okt 2008 21:34 Titel: |
 |
|
| Simo86 hat Folgendes geschrieben: | | Muss ich meine gleichung so aufbauen das vo abhängig ist von der Katapult länge. |
Ja, das hilft dir beim dritten der drei eben angesprochenen Punkte weiter. 
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 31. Okt 2008 11:29 Titel: Simo86 Verfasst am: 31. Okt 2008 11:29 Titel: |
 |
|
Also habe versucht weiter zu kommen. Aber irgendwie funktioniert das nicht. Ich komme mit t nicht klar. Was berhaupt eine winkelbeschleunigung sein soll und und und..
die Formel die ich als Schüler aus dem Tafelwerk bekomme
| Beschreibung: |
|

Download |
| Dateiname: |
Part 1.jpg |
| Dateigröße: |
64.49 KB |
| Heruntergeladen: |
5025 mal |
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 31. Okt 2008 11:29 Titel: Simo86 Verfasst am: 31. Okt 2008 11:29 Titel: |
 |
|
Mein Ansatz für v0
| Beschreibung: |
|

Download |
| Dateiname: |
Part 2.jpg |
| Dateigröße: |
67.41 KB |
| Heruntergeladen: |
4881 mal |
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 31. Okt 2008 11:30 Titel: Simo86 Verfasst am: 31. Okt 2008 11:30 Titel: |
 |
|
Weitere Gedanken die mir so eingefallen sind.
Aber ich weiß nicht wie ich eine Formel nach t umstellen kann und wie ich überhaupt diese winkelbeschleunigung beréchnen kann.
Also muss ich mein x und ho das ich sporalisch eingezeichnet habe mit berücksichtigen?????
| Beschreibung: |
|

Download |
| Dateiname: |
part 3.jpg |
| Dateigröße: |
53.72 KB |
| Heruntergeladen: |
3482 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 31. Okt 2008 12:14 Titel: dermarkus Verfasst am: 31. Okt 2008 12:14 Titel: |
 |
|
| Simo86 hat Folgendes geschrieben: |
Aber ich weiß nicht wie ich eine Formel nach t umstellen kann |
Oh, das erklärt natürlich einiges. Wie man Formeln umstellen kann, sollte man eigentlich schon längt im Schlaf wissen und geübt haben, bevor man sich an solche Aufgaben macht.
Das heißt, wir machen das ganze mal in deutlich kleineren Schritten und übersichtlicheren Portionen.
Dein (part 1) lassen wir erstmal außer acht, denn wir haben noch nicht überprüft, wie wir diese Formeln so verwenden können, dass sie auch wirklich zu dieser Aufgabe passen. Dein (part 2) lassen wir ebenfalls erstmal beiseite.
-------------------------------
Deine Zeichnung aus (part 3) finde ich prima  Da hast du bereits ganz viel von dem eingezeichnet, was du nun gut brauchen kannst Da hast du bereits ganz viel von dem eingezeichnet, was du nun gut brauchen kannst 
Wir werden es in dieser Aufgabe mit vielen Gleichungen zu tun bekommen. Also must du aufpassen, dass du mit jedem Variablennamen immer nur ganz genau eine Sache bezeichnest (und nicht mehrere Sachen gleichzeitig, sonst hat man beim Rechnen keine Chance). Deshalb schlage ich vor, folgende Variablen in deiner Zeichnung anders zu nennen:
Den Buchstaben x brauchen wir noch für etwas anderes. Lass uns die Streckenlänge, die du in deiner Skizze (part3) "x" genannt hast, lieber stattdessen 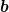 nennen. nennen.
Die Winkelbezeichnung "alpha" sollten wir uns lieber für den Winkel aufheben, unter dem das Geschoss mit der Geschwindigkeit 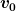 losfliegt. (Kannst du diesen Abflugwinkel alpha zusätzlich noch mit in deine Skizze (part3) einzeichnen?). Den Drehwinkel des Katapultes würde ich daher vorschlagen, mit dem griechischen Buchstaben phi ( losfliegt. (Kannst du diesen Abflugwinkel alpha zusätzlich noch mit in deine Skizze (part3) einzeichnen?). Den Drehwinkel des Katapultes würde ich daher vorschlagen, mit dem griechischen Buchstaben phi ( ) zu bezeichnen. Das heißt, wir sollten in der Skizze (part 3) das ) zu bezeichnen. Das heißt, wir sollten in der Skizze (part 3) das 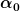 durch durch  und das und das  durch durch 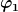 ersetzen. ersetzen.
Die Länge der Katapultstange heißt laut Aufgabenstellung 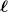 und beträgt 5 m. Magst du das noch mit in deine Skizze (part 3) mit einzeichnen? und beträgt 5 m. Magst du das noch mit in deine Skizze (part 3) mit einzeichnen?
Magst du mal das alles verwenden, um damit eine neue Skizze statt (part 3) zu zeichnen, damit wir diese neue Skizze dann als Ausgangspunkt für das Rechnen dieser Aufgabe nehmen können?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 31. Okt 2008 12:57 Titel: Simo86 Verfasst am: 31. Okt 2008 12:57 Titel: |
 |
|
So eine aufbesseung der skizze sowie weitere ansätze
| Beschreibung: |
|

Download |
| Dateiname: |
pic 4.jpg |
| Dateigröße: |
56.79 KB |
| Heruntergeladen: |
3975 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 31. Okt 2008 13:13 Titel: dermarkus Verfasst am: 31. Okt 2008 13:13 Titel: |
 |
|
Okay, einverstanden, dann nehmen wir jetzt mal im folgenden die Bezeichnungen, so wie du sie nun in dieser Skizze gewählt hast. (Deinen Versuch mit den Dreiecken darunter würde ich nicht vorschlagen, für diese Aufgabe weiter zu betrachten)
Nun müssen wir uns darum kümmern, dass die Variablenbezeichnung für die Flugzeit eindeutig wird. Denn "t" ist noch so allgemein, dass wir das sicher noch für mehrere Gleichungen brauchen werden, so dass das viel zu leicht zu Verwechslungen führt. Lass uns also die Zeit, die das Geschoss für seinen Flug zwischen Verlassen des Katapultes und Auftreffen an der Mauer braucht, mit 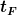 bezeichnen. bezeichnen.
Stellen wir nun die erste Gleichung auf, die wir konkret für diese Aufgabe brauchen können:
Wenn du die Abwurfgeschwindigkeit 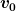 kennen würdest, kannst du dann damit eine Gleichung aufstellen, mit der man herausfinden kann, wie groß die Flugzeit kennen würdest, kannst du dann damit eine Gleichung aufstellen, mit der man herausfinden kann, wie groß die Flugzeit 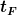 ist? ist?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 02. Nov 2008 19:50 Titel: Simo86 Verfasst am: 02. Nov 2008 19:50 Titel: |
 |
|
Aufgabe zur Berechnung der Winkelbeschleunigung
1 System (so lange das Objekt beschleunigt wird)
Ansatz (Berechnung von vo: )
Katapult fängt bei 5° (alpha) an zu beschleunigen bis zum Winkel 55°. Der dabei entstandene Weg (p) wird errechnet durch:
siehe Formel unten
Formel zur Berechnung von v = vo bzw. die maximale Geschwindigkeit erreicht hat:
siehe formel unten
Die Frage ist nun wie stark muss die Beschleunigung sein um die vo zu bestimmen, die dafür sorgt dass die Kugel die Mauer in der Höhe von 7 m erreicht, bei einer Weite von 50 m.
2 System (Objekt trennt sich vom Katapult und geht in einen schrägen Wurf über)
Ansatz (Wurfparabel):
Wurfparabel:
siehe formel unten
Meine Gedanken wäre nach vo umzustellen um die größe vo zu bestimmen, um zu wissen wie groß vo überhaupt sein muss. ???
Bestimmung von tan aplpha: siehe Bildzeichnung
Ich würde siehe Zeichnung…, dass Alpha sich aus Geometrischer Darstellung sich zeigen lässt.
Schluss Gedanken:
Also wenn ich nun weiß wie groß vo hypothetisch sein müsste… viel mir folgender Gedanke ein:
Formel zum Gedanken: vo= a t
Ich gehe davon aus ich wüsste vo. Also bestimmt die Zeit wie groß a wird. Aber woher soll ich wissen wie lange das Katapult braucht. Theoretisch kann jedes Katapult, je nachdem wie es beschaffen ist, eine andere Zeit benötigen.???? Oder ist der Gedanke unwichtig um die Winkelbeschleunigung zu berechnen? Da ich keine Vorstellung von einer Winkelbeschleunigung habe.
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 02. Nov 2008 19:52 Titel: Simo86 Verfasst am: 02. Nov 2008 19:52 Titel: |
 |
|
hier:
| Beschreibung: |
|
| Dateigröße: |
4.89 KB |
| Angeschaut: |
14143 mal |
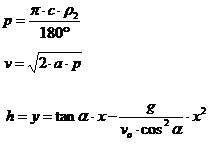
|
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 02. Nov 2008 19:53 Titel: Simo86 Verfasst am: 02. Nov 2008 19:53 Titel: |
 |
|
hier
| Beschreibung: |
|

Download |
| Dateiname: |
Der Feind.jpg |
| Dateigröße: |
8.32 KB |
| Heruntergeladen: |
3193 mal |
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 03. Nov 2008 12:55 Titel: Simo86 Verfasst am: 03. Nov 2008 12:55 Titel: |
 |
|
|
oder ist das Falsch
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. Nov 2008 13:30 Titel: dermarkus Verfasst am: 03. Nov 2008 13:30 Titel: |
 |
|
| Simo86 hat Folgendes geschrieben: |
Ansatz (Wurfparabel):
Wurfparabel:
siehe formel unten
Meine Gedanken wäre nach vo umzustellen um die größe vo zu bestimmen, um zu wissen wie groß vo überhaupt sein muss. ???
Bestimmung von tan aplpha: siehe Bildzeichnung
Ich würde siehe Zeichnung…, dass Alpha sich aus Geometrischer Darstellung sich zeigen lässt.
|
Ich finde, das klingt schonmal gut 
Beachte dabei folgendes: Überprüfe nochmal genau, ob deine Formel, die du für die Wurfparabel aufgeschreiben hast, nicht noch einen Fehler enthält: Muss bei dem 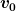 im Nenner nicht noch ein Quadrat dranstehen? im Nenner nicht noch ein Quadrat dranstehen?
Und dann muss du dir natürlich genau anschauen, welche Buchstaben in dieser Formel für die Wurfparabel gleich welchen Größen sind, die du bereits aus der Aufgabenstellung kennst. Magst du dafür mal eine sorgfältige Liste für alle Variablenbuchstaben in dieser Formel machen?
-----------------------------------------
| Zitat: |
Katapult fängt bei 5° (alpha) an zu beschleunigen bis zum Winkel 55°. Der dabei entstandene Weg (p) wird errechnet durch:
|
Vorsicht, der Winkel alpha war etwas anderes. Für die 5° hatten wir uns oben auf die Bezeichnung  geeinigt. geeinigt.
Ich finde es gut, dass du bereits die Formeln für eine beschleunigte Geradeaus-Bewegung kennst und aufschreiben kannst.
Denn die Formeln für eine Winkel-Bewegung mit konstanter Winkelbeschleunigung sehen genauso aus, nur eben mit den Winkelgrößen (zurückgelegte Winkeldifferenz, erreichte Winkelgeschwindigkeit, Winkelbeschleunigung) statt den Größen für eine Geradeausbewegung (zurückgelegte Wegdifferenz, erreichte Geschwindigkeit, Beschleunigung).
Hilft dir das beim Aufstellen von Formeln für die Winkelgrößen für die Beschleunigungsphase im Katapult?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 03. Nov 2008 17:56 Titel: Simo86 Verfasst am: 03. Nov 2008 17:56 Titel: |
 |
|
Stelle noch mal alle definierten Größen da:
h= gegebene Höhe=7m
l= gegebene Länge=50m
p0=5°
p2=50°
p1=55°
v0= Anfangsgeschwindigkeit
p= Katapultweg =Beschleunigungsweg
Alpha= Winkel der Wurfparabel=55°
c= Höhe des Katapult
mir gelingt es nicht nach v0 umustellen
| Beschreibung: |
|
| Dateigröße: |
1.98 KB |
| Angeschaut: |
14111 mal |
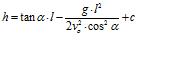
|
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. Nov 2008 18:23 Titel: dermarkus Verfasst am: 03. Nov 2008 18:23 Titel: |
 |
|
Da bin ich schon mit fast allem einverstanden 
Magst du noch dazusagen, wie du das
c="Höhe des Katapultes"
aus deinen Skizzen mit den gegebenen Größen ausrechnen kannst?
--------------------
Damit, dass du
l= gegebene Länge=50m
für das x in der Parabelgleichung eingesetzt hast, bin ich noch nicht ganz einverstanden. Schau mal genau in deine Skizzen: Wie lange ist der horizontale Weg x vom Abwurfpunkt bis zur Mauer wirklich genau?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 03. Nov 2008 18:41 Titel: Simo86 Verfasst am: 03. Nov 2008 18:41 Titel: |
 |
|
c für die Höhe wird umgeändert in b
c=Katapultlänge
k= Gesamtlänge=l+a
a=sin(55°)*c
k=29,096m
b²=c²-a²
b=2,87
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. Nov 2008 19:15 Titel: dermarkus Verfasst am: 03. Nov 2008 19:15 Titel: |
 |
|
Die Idee ist gut.
Magst du mal genau hinschauen und überprüfen, ob du bei dem a und dem b etwas Horizontales oder etwas Vertikales meinst? Und würdest du nicht auch erwarten, dass das k irgendwie größer als 50 m sein sollte?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 03. Nov 2008 19:21 Titel: Simo86 Verfasst am: 03. Nov 2008 19:21 Titel: |
 |
|
k ist k=54,096... falsch eingesetzt.....
k ist horizontal und b ist vertikal....
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 03. Nov 2008 22:59 Titel: Simo86 Verfasst am: 03. Nov 2008 22:59 Titel: |
 |
|
Jetzt weiß ich was mit vertikal und horizontal angedautet hast.
k=52,.....
K=50m+a
K=52,87
habe versucht nach vo umzustellen, ist diese Formel richtig.
Wenn nicht weiß ich auch nicht mehr weiter :-)
| Beschreibung: |
|
| Dateigröße: |
2.59 KB |
| Angeschaut: |
13842 mal |
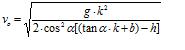
|
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 04. Nov 2008 00:35 Titel: dermarkus Verfasst am: 04. Nov 2008 00:35 Titel: |
 |
|
Prima  Einverstanden Einverstanden 
Dann kannst du dich nun der Frage widmen, wie du aus dem 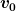 anhand des Beschleunigungsvorganges am Katapult die gesuchte Winkelbeschleunigung findest anhand des Beschleunigungsvorganges am Katapult die gesuchte Winkelbeschleunigung findest  Bringt dich dabei mein Tipp von oben zu den Winkelgrößen schon weiter? Bringt dich dabei mein Tipp von oben zu den Winkelgrößen schon weiter?
Hast du dir schon überlegt, mit welchem Variablenbuchstaben du die Winkelbeschleunigung bezeichnen möchtest? Im Zweifelsfall würde ich " Winkelbeschleunigung 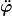 " vorschlagen, weil die Winkelbeschleunigung ja die zweite Ableitung des Winkels " vorschlagen, weil die Winkelbeschleunigung ja die zweite Ableitung des Winkels  nach der Zeit ist. nach der Zeit ist.
------------------
Kleiner Hinweis zur Schreibweise am Rande: Der griechische Buchstabe phi sieht so aus:  . Ein anderer griechischer Buchstabe ist das . Ein anderer griechischer Buchstabe ist das 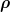 , das ist kein phi, sondern ein rho. , das ist kein phi, sondern ein rho.
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 04. Nov 2008 16:20 Titel: Simo86 Verfasst am: 04. Nov 2008 16:20 Titel: |
 |
|
|
Also wie ich die winkelbeshcl. ausrechnen soll weiß ich nicht. wenn ich eine Formel habe, sind 2 unbekannte drin a und t... und wenn ich eine zur anderen umstelle ist immernoch eine unbekannte mit drin.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 04. Nov 2008 18:28 Titel: dermarkus Verfasst am: 04. Nov 2008 18:28 Titel: |
 |
|
|
Tipp: Wie hast du vorhin so eine vergleichbare Formel für die Größen der linearen Bewegung aufgestellt?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 04. Nov 2008 19:04 Titel: Simo86 Verfasst am: 04. Nov 2008 19:04 Titel: |
 |
|
die strecke habe ich ausrechnet, also p und den rest v=wurzel(2ap) habe ich aus dem Tafelwerk... um v zu berechnen. Soll ich daraus a bestimmen. wie weit würde mich das dann zur winkelbeschleunigung bringen????
ist die v formel überhaupt richtig für die Katapult geschwindigkeit???
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 04. Nov 2008 19:39 Titel: dermarkus Verfasst am: 04. Nov 2008 19:39 Titel: |
 |
|
| Simo86 hat Folgendes geschrieben: |
ist die v formel überhaupt richtig für die Katapult geschwindigkeit??? |
Magst du das am besten selbst mal überprüfen?
Gehe ich recht in der Annahme, dass du die Formeln
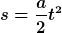
und

für eine gleichmäßig beschleunigte lineare Bewegung schon mal gesehen hast? Kannst du daraus eine Formel für die Endgeschwindigkeit  herleiten, die nur noch von der Beschleunigung herleiten, die nur noch von der Beschleunigung  und der zurückgelegten Strecke und der zurückgelegten Strecke  abhängt? abhängt?
-------------------
Wie lauten die analogen Gleichungen für die Winkelgrößen? Kannst du dir auch da einen Zusammenhang zwischen erreichter Winkelgeschwindigkeit, zurückgelegtem Winkel und Winkelbeschleunigung für eine Kreisbewegung mit konstanter WInkelbeschleunigung herleiten?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 04. Nov 2008 20:34 Titel: Simo86 Verfasst am: 04. Nov 2008 20:34 Titel: |
 |
|
also v=wurzel(2ap) stimmt 
wenn ich das nach a ausrichte erhalte ich
a= (vo^2)/(2p)
mit winkel bin ich noch am gucken
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 05. Nov 2008 10:41 Titel: Simo86 Verfasst am: 05. Nov 2008 10:41 Titel: |
 |
|
Bevor ich weiter rechne... ist a richtig... denn wenn ich a ausrechne bekomme ich was mit ca. über 60 .... ist das nicht zu hoch.. das hieße ja das Katapult bracht noc nicht mal eine Sekunde bis es vo erreicht hat....
paar Formel aus der gleichförmigern Kreisbewegung
v=w r
w=v/r
a=v^2 /r
a=w^2 / r
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 05. Nov 2008 14:31 Titel: dermarkus Verfasst am: 05. Nov 2008 14:31 Titel: |
 |
|
| Simo86 hat Folgendes geschrieben: | Bevor ich weiter rechne... ist a richtig... denn wenn ich a ausrechne bekomme ich was mit ca. über 60 ....
|
Wenn du die Formel für die Winkelgrößen hast, dann brauchst du gar kein a mehr auszurechnen. (Und Vorsicht, Ergebnisse ohne Einheit haben keine physikalische Aussagekraft.)
| Zitat: |
paar Formel aus der gleichförmigern Kreisbewegung
v=w r
w=v/r
|
Einverstanden, das wirst du hier brauchen können. Was bedeuten die Buchstaben in diesen Gleichungen, und kannst du folglich damit eine Gleichung aufstellen, die zu den Variablenbezeichnungen, die du hier in der Aufgabe gewählt hast, passt?
| Zitat: |
a=v^2 /r
a=w^2 / r |
Vorsicht, erstens muss es in der zweiten dieser Formeln "*r" statt "/r" heißen, und zweitens ist dieses a ein ganz anderes a als das, von dem du oben mal gesprochen hast. Was bedeuten die Größen in diesen Gleichungen, und warum ist es folglich nicht nötig, diese Formeln hier zu verwenden?
----------------------
Um die gesuchte Winkelbeschleunigung des Katapultes auszurechnen, fehlen dir nach wie vor einfach noch die Gleichungen für die Winkelgrößen, die du analog für eine lineare Bewegung hier schon hingeschreiben hast.,
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 05. Nov 2008 15:28 Titel: Simo86 Verfasst am: 05. Nov 2008 15:28 Titel: |
 |
|
w=v*c
aber gilt das nicht wenn v=konst ist. Aber V ist beim Katapult nocht nicht kontstant. ????
Also bei der Winkelbeschnlleunigung blicke ich nicht durch....
Normal würde man es s=0.5 a t^2 ausrechnen .... und die benötigen Parameter dann umstellen... aber wie soll das denn bei einer Winkelbeschleunigung sein...
ich habe p, a muss von phi bestimmt anbhängig sein.... und r=c brauche ich bestimmt..... aber mir fehlt der blick daraus einen zusammenhang zu sehen
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 05. Nov 2008 15:50 Titel: Simo86 Verfasst am: 05. Nov 2008 15:50 Titel: |
 |
|
Also ich denke das ich p nicht brauche für Winkelbeschleunigung sitimmts.. da r und alpha denn weg dann denke ich beschreiben würde....
| Beschreibung: |
|

Download |
| Dateiname: |
katapult.jpg |
| Dateigröße: |
14.98 KB |
| Heruntergeladen: |
2724 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 05. Nov 2008 15:53 Titel: dermarkus Verfasst am: 05. Nov 2008 15:53 Titel: |
 |
|
Nimm mal nur die Winkelgrößen (wie nennst du den zurückgelegten Winkel, die Winkelgeschwindigkeit , die Winkelbeschleunigung als Variablenbezeichnungen in dieser Aufgabe?) und das c. (und das v_0).
Welche Gleichungen kannst du damit aufstellen?
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 05. Nov 2008 16:00 Titel: Simo86 Verfasst am: 05. Nov 2008 16:00 Titel: |
 |
|
| Zitat: |
Nimm mal nur die Winkelgrößen (wie nennst du den zurückgelegten Winkel, die Winkelgeschwindigkeit , die Winkelbeschleunigung als Variablenbezeichnungen in dieser Aufgabe?) und das c. (und das v_0).
Welche Gleichungen kannst du damit aufstellen?
|
Alpha=zurückgelegter Winkel
w=Winkelgeschwindigkeit ( w= v/t)
q(alpha)= Winkebeschleunigung.... <= da ich denke das die Beschleunigung abhängig vom Winkel ist
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 06. Nov 2008 02:04 Titel: Simo86 Verfasst am: 06. Nov 2008 02:04 Titel: |
 |
|
Vllt sehe ich ja morgen früh noch die antwort... um 9 uhr muss ich die aufgaben abgeben.... sonst danke ich für die Hilfe 
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 06. Nov 2008 02:57 Titel: dermarkus Verfasst am: 06. Nov 2008 02:57 Titel: |
 |
|
| Simo86 hat Folgendes geschrieben: |
Alpha=zurückgelegter Winkel
w=Winkelgeschwindigkeit ( w= v/t)
q(alpha)= Winkebeschleunigung.... <= da ich denke das die Beschleunigung abhängig vom Winkel ist |
Das würde ich anders schreiben:
zurückgelegter Winkel : 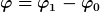
nach der Winkelbeschleunigungsphase im Katapult erreichte Winkelgeschwindigkeit: 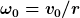
Winkelbeschleunigung: 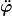
(Beschleunigungsdauer 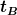 ) )
Für diese Winkelgrößen gelten in einer gleichmäßig beschleunigten Kreisbewegung genau die analogen Gleichungen wie für die Größen s, v und a in einer gleichmäig beschleunigten linearen Beschleunigung, also zum Beispiel auch:
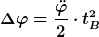
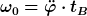
|
|
 |
Simo86
Anmeldungsdatum: 30.10.2008
Beiträge: 106
|
 Simo86 Verfasst am: 06. Nov 2008 03:50 Titel: Simo86 Verfasst am: 06. Nov 2008 03:50 Titel: |
 |
|
|
kann ich damit die winkelbeschleunigung ausrechnen....???
|
|
 |
|