| Autor |
Nachricht |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 13:27 Titel: Parallel - Schwingkreis Ricky Verfasst am: 22. Mai 2011 13:27 Titel: Parallel - Schwingkreis |
 |
|
Hallo folgende Aufgabe :
| Beschreibung: |
|

Download |
| Dateiname: |
Unbenannt.JPG |
| Dateigröße: |
24.55 KB |
| Heruntergeladen: |
2503 mal |
Zuletzt bearbeitet von Ricky am 22. Mai 2011 13:29, insgesamt einmal bearbeitet |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 13:28 Titel: Ricky Verfasst am: 22. Mai 2011 13:28 Titel: |
 |
|
zu Aufgabenteil a )
wäre die Gesamtimpedanz doch :

oder...?
aber das kann man doch bestimmt noch irgendwie dann vereinfachen
oder.. 
|
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 22. Mai 2011 14:25 Titel: Chillosaurus Verfasst am: 22. Mai 2011 14:25 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | [...]
wäre die Gesamtimpedanz doch :
 [...] [...] |
1. Gesamtimpedanz = Wechselstromwiderstand
--> Formel nicht Richtig, da die Einheit OHM sein muss.
Vorgehen: R,L in Reihe Z=R+Zl, C parallel dazu:
Zg=(1/Zc + 1/Z)^-1
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 14:44 Titel: Ricky Verfasst am: 22. Mai 2011 14:44 Titel: |
 |
|
also gilt für die Geamtimpedanz :
^{-1})
^{-1})
^{-1})



 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 15:02 Titel: Ricky Verfasst am: 22. Mai 2011 15:02 Titel: |
 |
|
oder ist das so richtig...?
| Beschreibung: |
|

Download |
| Dateiname: |
Unbenannt2.JPG |
| Dateigröße: |
39.59 KB |
| Heruntergeladen: |
2449 mal |
|
|
 |
pete2011
Gast
|
 pete2011 Verfasst am: 22. Mai 2011 15:04 Titel: pete2011 Verfasst am: 22. Mai 2011 15:04 Titel: |
 |
|
Ratestunde? 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 15:09 Titel: Ricky Verfasst am: 22. Mai 2011 15:09 Titel: |
 |
|
Nein, ich suche einfach nur hilfe , weil ich starke schwierigkeiten bei
der aufgabe habe...  
|
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 22. Mai 2011 15:57 Titel: Chillosaurus Verfasst am: 22. Mai 2011 15:57 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | also gilt für die Geamtimpedanz :
^{-1}) [...] [...] |
Wo ist denn jetzt dein Ohmscher Widerstand hin??
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 15:59 Titel: Ricky Verfasst am: 22. Mai 2011 15:59 Titel: |
 |
|
upppsss....es sollte heissen :
^{-1})
|
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 22. Mai 2011 16:09 Titel: Chillosaurus Verfasst am: 22. Mai 2011 16:09 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | upppsss....es sollte heissen :
^{-1}) |

|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 16:15 Titel: Ricky Verfasst am: 22. Mai 2011 16:15 Titel: |
 |
|
Ja, soweit so gut...aber das ist doch nun noch nicht alles gewesen oder...
muss ich nun damit nicht noch irgendwie weiterrechne, umformen
oder so...?
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 22. Mai 2011 16:55 Titel: GvC Verfasst am: 22. Mai 2011 16:55 Titel: |
 |
|
Ja, wie in der Aufgabenstellung vorgegeben: die Impedanz in Abhängigkeit von w darstellen.
Da Du ja auch noch die Phasenverschiebung in Abhängigkeit von der Kreisfrequenz darstellen sollst, ist es sinnvoll, die Impedanz in kartesischer Form darzustellen, also als Realteil + j*Imaginärteil.
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 17:00 Titel: Ricky Verfasst am: 22. Mai 2011 17:00 Titel: |
 |
|
ok...und könnt ihr mir vielleicht dabei helfen... 
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 22. Mai 2011 17:08 Titel: GvC Verfasst am: 22. Mai 2011 17:08 Titel: |
 |
|
|
Fang doch mal damit an. Wie drückst Du Zc aus, wie drückst Du ZL aus? Was machst Du, wenn Du einen komplexen Ausdruck im Nennner vorfindest? Das sind doch alles Standardroutinen. Mach' mal!
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 17:18 Titel: Ricky Verfasst am: 22. Mai 2011 17:18 Titel: |
 |
|
also es gilt :
^{-1})
also :
^{-1})


soweit richtig...?
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 19:30 Titel: Ricky Verfasst am: 22. Mai 2011 19:30 Titel: |
 |
|
falls das so richtig ist, dann weiss ich nun nicht, wie ich weiter machen
soll...  
|
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 22. Mai 2011 20:01 Titel: Chillosaurus Verfasst am: 22. Mai 2011 20:01 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | also es gilt :
^{-1})
also :
^{-1})
[...] |
Da stimmt doch schonmal irgendetwas nicht.
|
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 22. Mai 2011 20:06 Titel: Chillosaurus Verfasst am: 22. Mai 2011 20:06 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | also es gilt :
^{-1})
also :
[...]


soweit richtig...? |
Aha, da scheint es doch wieder richtig zu sein.
In der folgenden Zeile hast du aber versehentlich multipliziert statt addiert. Mach die Umformung des Bruches nochmal Schritt für Schritt.
Wie wirst du denn den komplexen Nenner los, das dürftest du aus der Einführung o.ä. noch kennen oder?
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 20:21 Titel: Ricky Verfasst am: 22. Mai 2011 20:21 Titel: |
 |
|
ich bin mir jetzt nicht sicher, bei der umformung des bruches
ist es so

und dann müsste ich mit dem konjugiert komplexen Ausdruck des Nenners erweitern oder.. 
also :

\cdot(iwC-1)}{(iwC+1)\cdot(iwC-1)})


Zuletzt bearbeitet von Ricky am 22. Mai 2011 20:32, insgesamt einmal bearbeitet |
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 22. Mai 2011 20:30 Titel: Chillosaurus Verfasst am: 22. Mai 2011 20:30 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | [...]
ist es so
 [...] [...] |
Nein, ganz gewiss nicht. Du hast doch geschrieben erweitern ist dir ein Begriff. Wie addiert man Brüche...
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 20:36 Titel: Ricky Verfasst am: 22. Mai 2011 20:36 Titel: |
 |
|
indem man sie gleichnamig macht...aber ich wollte erst einmal die doppelbrüche auflösen , indem ich mit dem kehrwert multipliziere...
wäre das dann

 
|
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 22. Mai 2011 21:23 Titel: Chillosaurus Verfasst am: 22. Mai 2011 21:23 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | | indem man sie gleichnamig macht...[...] |
Dann mach das doch: Berechne den Nenner von Zg und bilde dann den Kehrwert.
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 22. Mai 2011 22:00 Titel: Ricky Verfasst am: 22. Mai 2011 22:00 Titel: |
 |
|
Ja, das würde ich ja, denn bei einem einfachen bruch ist das mit dem gleichnamig machen einfach...aber bei diesem kompliziertem ausdruck, weiss ich nicht wie ich da vorgehen muss...ich hab wirklich keine ahnung...  
|
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 22. Mai 2011 22:29 Titel: Chillosaurus Verfasst am: 22. Mai 2011 22:29 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | [...]

[...] |
Erst den Nenner ausrechnen, dann das Reziproke bilden. Da ist nichts kompliziertes dran. Ersteres habe ich in der 4. Klasse gelernt.
Wenn du das nicht hinkriegst, bringt es wenig, wenn wir dir hier Hilfestellungen geben, da musst du dir das ganze nochmal gründlich erarbeiten.
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 23. Mai 2011 08:45 Titel: Ricky Verfasst am: 23. Mai 2011 08:45 Titel: |
 |
|
Tut mir leid, aber ich komme da wirklich
nicht weiter...
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 23. Mai 2011 12:24 Titel: Ricky Verfasst am: 23. Mai 2011 12:24 Titel: |
 |
|
Also ich müsste das ja nun irgendwie berechnen :

aber ich weiss wirklich nicht wie, denn dieser doppelbruch im ersten
term macht mir zu schaffen...  
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 12:34 Titel: Keplerfan Verfasst am: 23. Mai 2011 12:34 Titel: |
 |
|

Ich würde dir vorschlagen, zunächst nur den Nenner zu berechnen, also das:

Nun zunächst diese beiden getrennt.
Wie lässt sich der Bruch  vereinfachen? vereinfachen?
Beim zweiten musst du mit dem konjugiert Komplexen von 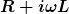 erweitern, um den komplexen Nenner reell zu machen. erweitern, um den komplexen Nenner reell zu machen.
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 12:36 Titel: Keplerfan Verfasst am: 23. Mai 2011 12:36 Titel: |
 |
|
Einfaches Beispiel zum Eingeben in den Taschenrechner: Was ist
} ) ? ?
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 23. Mai 2011 12:43 Titel: Ricky Verfasst am: 23. Mai 2011 12:43 Titel: |
 |
|
| Keplerfan hat Folgendes geschrieben: | Wie lässt sich der Bruch  vereinfachen? vereinfachen? |

oder...?
| Keplerfan hat Folgendes geschrieben: |
Beim zweiten musst du mit dem konjugiert Komplexen von 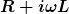 erweitern, um den komplexen Nenner reell zu machen. erweitern, um den komplexen Nenner reell zu machen. |
also :
\cdot\left(\frac{R-iwL}{R-iwL}\right))
oder...?
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 12:45 Titel: Keplerfan Verfasst am: 23. Mai 2011 12:45 Titel: |
 |
|
Korrekt. 
Nun den Bruch mit dem R bitte noch ausrechnen.
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 23. Mai 2011 13:27 Titel: Ricky Verfasst am: 23. Mai 2011 13:27 Titel: |
 |
|
Ok, gut! Wäre das dann :


Wobei das doch wieder mein ausgangsproblem
wäre...
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 13:30 Titel: Keplerfan Verfasst am: 23. Mai 2011 13:30 Titel: |
 |
|
Oben stimmts, unten nicht. Löse mal in Ruhe die Klammer
(R-i \omega L) ) auf und beachte auf und beachte  . .
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 13:33 Titel: Keplerfan Verfasst am: 23. Mai 2011 13:33 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: |
[...]

[...]
|
Das kann man so nicht kürzen ... Du solltest dir dringend nochmal die Rechenregeln der komplexen Zahlen anschauen.
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 23. Mai 2011 14:02 Titel: Ricky Verfasst am: 23. Mai 2011 14:02 Titel: |
 |
|
Ok...nochmal mein versuch:

Nun richtig...?
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 14:02 Titel: Keplerfan Verfasst am: 23. Mai 2011 14:02 Titel: |
 |
|
Perfekt. 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 23. Mai 2011 14:14 Titel: Ricky Verfasst am: 23. Mai 2011 14:14 Titel: |
 |
|
Also wäre das dann nun meine Lösung zu aufgabenteil
a)

...?
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 14:17 Titel: Keplerfan Verfasst am: 23. Mai 2011 14:17 Titel: |
 |
|
Zur Erinnerung: Zu berechnen war der Ausdruck

Und das ist nur der Nenner deiner Gesamt-Impedanz  . .
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 23. Mai 2011 14:36 Titel: Ricky Verfasst am: 23. Mai 2011 14:36 Titel: |
 |
|
| Keplerfan hat Folgendes geschrieben: | Zur Erinnerung: Zu berechnen war der Ausdruck

Und das ist nur der Nenner deiner Gesamt-Impedanz  . . |
Achja stimmt...und wie muss ich nun weiterrechnen
um auf meine gesamtimpedanz zu kommen...?
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 14:38 Titel: Keplerfan Verfasst am: 23. Mai 2011 14:38 Titel: |
 |
|
Probier doch mal ein bisschen.
 und den anderen Ausdruck auf einen gemeinsamen Nenner zu bringen wäre sicher eine gute Idee. und den anderen Ausdruck auf einen gemeinsamen Nenner zu bringen wäre sicher eine gute Idee.
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 23. Mai 2011 14:53 Titel: Ricky Verfasst am: 23. Mai 2011 14:53 Titel: |
 |
|
Also wäre das dann :
}{R^2+w^2L^2} +\frac{R-iwL}{R^2+w^2 L^2})
|
|
 |
|




















