| Autor |
Nachricht |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 26. März 2009 18:44 Titel: Resonanz im Schwingkreis _-Alex-_ Verfasst am: 26. März 2009 18:44 Titel: Resonanz im Schwingkreis |
 |
|
Tach,
ich wollte mal fragen, ob die im Resonanzfall auftretende Phasenverschiebung um phi/2 automatisch auftritt, wenn die entsprechende Frequenz vorhanden ist. Oder ob man auf die Phasenverschiebung selber auch noch achten muss, dass sie phi/2 beträgt.
Weil wenn ich mir nur die 2 Frequenzen vorstelle, könnten sie doch eigentlich auch anders verschoben sein.
MfG
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 26. März 2009 21:22 Titel: Re: Resonanz im Schwingkreis schnudl Verfasst am: 26. März 2009 21:22 Titel: Re: Resonanz im Schwingkreis |
 |
|
Ohne dir jetzt nahetreten zu wollen - das ist ein typisches Beispiel für einen unüberlegten Post auf den man normalerweise keine Antwort bekommt, da die Frage völlig nebulos und unzureichend formuliert ist:
| _-Alex-_ hat Folgendes geschrieben: | ich wollte mal fragen, ob die im Resonanzfall
1) welches System betrachtest du hier? Wenn schon keine Zeichnung, dann sollte wenigstens eine kleine Erklärung des hinterfragten Objekts (OK - irgendein Schwingkreis - aber ist es ein Parallelschwingkreis, ein Serienschwingkreis, einer mit Dämpfung, ohne Dämpfung, freischwingend oder mit Einkopplung, ...) gegeben werden
auftretende Phasenverschiebung
2) Phasenverschiebung zwischen welchen Grössen ? EIne Phasenverschiebung bezieht sich immer auf zwei Grössen. Du gibst nicht mal eine davon an.
um phi/2 automatisch auftritt, wenn die entsprechende Frequenz vorhanden ist.
3) was meinst du mit "vorhanden" ?
Oder ob man auf die Phasenverschiebung selber auch noch achten muss, dass sie phi/2 beträgt.
Weil wenn ich mir nur die 2 Frequenzen vorstelle
4) welche zwei Frequenzen ???
, könnten sie doch eigentlich auch anders verschoben sein.
5) für zwei verschiedene Frequenzen ist eine Phasenverschiebung nicht (so ohne weiteres) definierbar. Was meinst du daher?
MfG |
Verstehst du nun, was ich meine ? 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 27. März 2009 13:32 Titel: _-Alex-_ Verfasst am: 27. März 2009 13:32 Titel: |
 |
|
Das war jetzt nicht direkt eine Aufgabe, bei der etwas gegeben war.
Wir haben vorab eine mechanische Schwingung betrachtet. Der Lehrer hat dazu eine Feder genommen und ein Gewicht drangehangen. Und das dann halt pendeln lassen und mit seiner Hand verschieden Frequenzen, die im vergleich zu der des Gewichtes, welches pendelt, entweder viel kleiner, viel größer oder gleich waren.
Bei dem Resonanzfall wurde dann gesagt, dass die beiden Frequenzen gleich sind, und eine Phasenverschiebung zwischen den beiden Frequenzen von Erreger und dem Gewicht um phi/2 vorlag.
Bei sehr kleiner Erregerfrequenz war die Verschiebung 0 und bei sehr großer phi.
Das waren jetzt unsere Beobachtungen.
Meine erste Frage zu dem mechanischen Beispiel war die, ob diese Phasenverschiebung im Resonanzfall um phi/2 automatisch, also von alleine kommt. Oder ob man neben der passenden Frequenz auch noch darauf achten muss. Also sozusagen ob ich, um auf das Beispiel mit der Hand als Erreger zurückzukommen, darauf achten muss, dass ich meine Hand im richtigen Moment bewege. Oder ob es einfach reicht, dass ich meine Hand mit der gleichen Frequenz bewege und die Phasenverschiebung eben von alleine erscheint. Weil ich hab halt irgendwie gedacht, dass selbst wenn mein Erreger die gleiche Frequenz wie die Eigenfrequenz von meinem Gewicht hier hat, kann ich ja immer noch sozusagen im falschen Moment "mit meiner Hand das Maximum meiner Bewegung" erreichen und rege somit den Körper nicht im richtigen Moment an.
Das war ja jetzt mechanisch, aber ich weiß eben auch nicht genau, wie der Vorgang dann auf den elektrischen Schwingkreis übertragen soll.
Also wenn ich jetzt irgendeinen elektrischen Schwingkreis habe. Der schwingt ja nun, und wegen dem Energieverlust wird die Schwingung immer schwächer. Jetzt will ich ja, dass der konstant bleibt. Wie bei dem Gewicht im Mechanischen. Im Mechanischen habe ich ja meine Hand als Erreger gehabt, im elektrischen wäre ja das Gegenstück eine Wechselstromquelle oder? Damit ich ja ein Gerät habe, welches sozusagen auch "schwingt".
Reicht jetzt bei dem Kreis, dass ich das Gerät anschließe und einen Strom mit der Gleichen Frequenz fließen lasse, wie mein Schwingkreis, oder muss ich irgendwie noch auf die Phasenverschiebung achten, damit es in dem elektrischen Schwingkreis zur Resonanz kommt?
EDIT:
Oder hat diese Resonanzfrequenz nichts mit der Frequenz meines "Schwingers" zu tun und ich muss mit meinem Erreger nur eine bestimmte Schwingung mit eben einer bestimmten Frequenz ausüben und alles erledigt sich von selbst oO?
MfG
PS^^: Ja deine Einwände waren sehr berechtigt:D. Ich hoffe so versteht man mich besser 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 27. März 2009 17:40 Titel: schnudl Verfasst am: 27. März 2009 17:40 Titel: |
 |
|
Das ist schon viel besser beschrieben 
Du musst unterscheiden zwischen der Anregung und der Schwingungsamplitude die sich daraus ergibt.:
Die Anregung (=Ursache) ist eine Kraft F(t), die durch die Hand auf die Mase wirkt
Als Reaktion (=Wirkung) stellt sich eine Schwingung mit bestimmter Amplitude y(t) ein.
Zwischen Wirkung und Ursache gibt es einen genauen Zusammenhang, der durch eine sog. Übertragungsfuktion beschrieben wird. Wenn du mit einer sinusförmigen Kraft
 = F_0 \cdot \cos (\omega t))
anregst, so wirst du nach einiger Zeit eine ebenfalls sinusförmige Auslenkung y(t) der Masse feststellen, wenn das System gedämpft ist:
 = y_0(\omega) \cdot \cos (\omega t+\varphi(\omega)))
Dabei ist
 = \frac{F_0}{\sqrt{(C-m \omega^2 )^2+\omega^2 D^2}})
(--korrigiert--)
und
 = -\frac{\omega D}{C-m\omega^2})
D ist hier die Dämpfungskonstante und C die Federkonstante.
Bei Resonanz ist

und

was nichts anderes bedeutet als

Bei 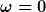 ist ist
 = -\frac{-0}{C} = -0)
und somit

also im 4. Quadranten
Bei sehr hohen Frequenzen ist
 = -\frac{\infty D}{C-m \cdot \infty^2} = +0)
was einer Phase von

im 3. Quadranten entspricht.
Insgesamt wandert die Phasenverschiebung also von -0° (bei w=0) über -90° (bei Resonanz) nach -180° (w sehr gross).
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe)
Zuletzt bearbeitet von schnudl am 06. Apr 2009 11:25, insgesamt 2-mal bearbeitet |
|
 |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 27. März 2009 20:04 Titel: _-Alex-_ Verfasst am: 27. März 2009 20:04 Titel: |
 |
|
Lernt man das noch im Gymnasium? Weil so genau haben wir das nicht gemacht  , darum weiß ich jetzt auch nicht wieso das so ist mit den Formeln. , darum weiß ich jetzt auch nicht wieso das so ist mit den Formeln.
Ich hab hier 3 Sätze in dem Buch gefunden:
1.
Man kann einen Oszillator zu erzwungenen Schwingungen anregen. Die Erregerfrequenz ist dabei stets gleich der Oszillatorfrequenz.
2.
Bei gleicher Erregeramplitude sind jedoch die Oszillatoramplitude und auch die Phasenverschiebung zwischen beiden Schwingungen von der Erregerfrequenz abhängig.
3.
Im Resonanzfall (f=f0) erreicht die Oszillatoramplitude ein Maximum. Die Erregerschwingung eilt der Oszillatorschwingung um phi/2 voraus. In diesem Fall ist die Energiezufuhr vom Erreger zum Oszillator optimal.
Also heißt das jetzt, wenn ich einen Körper habe der mit der Frequenz f0 schwingt, muss ich einen Erreger haben, vielleicht meine Hand, der die Gleiche Frequenz hat, damit es zu einer erzwungenen Schwingung kommt?
Der erste Punkt besagt ja noch nicht, dass es der Resonanz Fall ist - eigentlich  . Jetzt steht ja doch bei dem dritten Punkt, dass im Resonanzfall f und f0 gleich sind. Also schon die Situation wie oben beschrieben herrschen muss? (Ich mach jetzt ein paar viele Fragezeichen hin:D weil ich mir echt net sicher bin:( ) Und dass im Resonanzfall eine Phasenverschiebung um phi/2 vorliegen muss. . Jetzt steht ja doch bei dem dritten Punkt, dass im Resonanzfall f und f0 gleich sind. Also schon die Situation wie oben beschrieben herrschen muss? (Ich mach jetzt ein paar viele Fragezeichen hin:D weil ich mir echt net sicher bin:( ) Und dass im Resonanzfall eine Phasenverschiebung um phi/2 vorliegen muss.
Und ich hab das halt so aufgefasst, dass wenn ich Resonanz haben will. Ich darauf achten muss, dass meine Hand sich mit der gleichen Frequenz wie mein Körper bewegen muss UND dass ich die Phasenverschiebung um phi/2 beachten muss. Ich finde halt, dass sich das so anhört. Weil nach Punkt 1, ist es ja noch keine Resonanz wenn die Frequenzen gleich sind, oder ist das mit erzwungener Schwingung gemeint?
Und mich hat halt dann noch mehr verwirrt, dass einer in der Schule meinte. Dass die Phasenverschiebung automatisch käme, sobald ich an meinen Erreger die Resoanzfrequenz des Körpers "anlege". Ich fand halt, dass sich das anders anhört.
Ein anderer Punkt war der, das er gesagt hat. Dass die Resonanzfrequenz, nicht von der Frequenz abhängt, mit der mein Körper schwingt. Sondern dass das irgendeine ist.
Ich dachte halt wiederum, dass wenn mein Körper mit einer Frequenz von sagen wir 2 schwingt. Dass ich einen Erreger brauche, der ebenfalls mit einer Frequenz von 2 schwingt, aber zusätzlich noch mit einer Phasenverschiebung von phi/2, damit die Energiezufuhr optimal ist.
Und das haben wir leider nicht wirklich genau durchgesprochen gehabt, zumindest so, dass es mich zufrieden stellt ^.^
MfG
EDIT: Falls das nicht im Gym mehr dran kommt was du eben für Formeln da genannt hast. Kannst du mir dann das Buch verraten, in dem das drin steht, falls es da eins gibt 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 27. März 2009 21:14 Titel: schnudl Verfasst am: 27. März 2009 21:14 Titel: |
 |
|
Du verwechselst zwischen erzwungener und freier Schwingung.
Die freie Schwingung ist, wenn du den Federschwinger einmal auslenkst und dann eben frei schwingen lässt. Das läuft mit einer Eigenfrequenz f0. Wegen der Dämpfung wird die Amplitude aber allmählich kleiner und verschwindet schliesslich.
Wenn du eine periodische Kraft der Frequenz f anlegst, so wird der Federschwinger jedoch nicht mit seiner Eigenfrequenz f0, sondern mit f schwingen, und zwar ungedämpft. Die Amplitude der entstehenden Auslenkung und die Phasenverschiebung zwischen Erregerkraft und Auslenkung sind allerdings von dieser angelegten Frequenz abhängig. Das ist gleichbedeutend mit den Aussagen 1 und 2.
| Zitat: | 3.
Im Resonanzfall (f=f0) erreicht die Oszillatoramplitude ein Maximum. Die Erregerschwingung eilt der Oszillatorschwingung um phi/2 voraus. In diesem Fall ist die Energiezufuhr vom Erreger zum Oszillator optimal. |
| Zitat: |
Also heißt das jetzt, wenn ich einen Körper habe der mit der Frequenz f0 schwingt, muss ich einen Erreger haben, vielleicht meine Hand, der die Gleiche Frequenz hat, damit es zu einer erzwungenen Schwingung kommt? |
Nein, der Körper schwingt immer mit der Frequenz, die du vorgibst. Die sich einstellende Amplitude wird aber von der Frequenz abhängen. Die grösste Amplitude ergibt sich bei Resonanz. Bei dieser Frequenz eilt die Amplitude der Erregerkraft um 90° nach. Normalerweise ist die Resonanzfrequenz sehr nahe bei der Eigenfrequenz.
| Zitat: | | Und ich hab das halt so aufgefasst, dass wenn ich Resonanz haben will. Ich darauf achten muss, dass meine Hand sich mit der gleichen Frequenz wie mein Körper bewegen muss UND dass ich die Phasenverschiebung um phi/2 beachten muss. |
Nein, du musst nur die Frequenz der Kraft so vorgeben, dass diese der Resonanzfrequenz entspricht. Wie gesagt, ist dies normalerweise sehr nahe bei der Eigenfrequenz. Auf die Phase musst du nicht mehr achten. Du kannst ja nur die Kraft vorgeben, die Auslenkung stellt sich dazu automatisch ein, und bei Resonanz ist die Phase wie gesagt -90°.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 27. März 2009 22:12 Titel: _-Alex-_ Verfasst am: 27. März 2009 22:12 Titel: |
 |
|
Och man 
Ich hab eben ein bisschen rumgegoogelt. Und dabei leider gefunden, dass das zum 11.Klassstoff gehört, aber wir das nicht wirklich gemacht haben. Zumindest nicht in der Ausführlichkeit.
Ich bin dabei auf diese Simulation gestoßen.
http://www.walter-fendt.de/ph14d/resonanz.htm
Hier ist doch w0 (mein klein Omega ist w) die Eigenfrequenz von meinem blauen Körper. Und wenn ich die rote Frequenz meines Erregers auf 0 stelle, schwingt ja auch mein blauer Körper mit der Frequenz und die Schwingung wird immer schwächer. Und im Resonanzfall muss ja die Frequenz von beiden gleich sein und das ist da doch dann die Eigenfrequenz, mit der mein blauer Körper auch ohne die Frequenz vom Erreger schwingen würde.
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 27. März 2009 23:18 Titel: para Verfasst am: 27. März 2009 23:18 Titel: |
 |
|
| _-Alex-_ hat Folgendes geschrieben: | 3.
Im Resonanzfall (f=f0) erreicht die Oszillatoramplitude ein Maximum. Die Erregerschwingung eilt der Oszillatorschwingung um phi/2 voraus. In diesem Fall ist die Energiezufuhr vom Erreger zum Oszillator optimal. |
Kleine Ergänzung: Der erste Satz ist meiner Meinung nach nicht ganz exakt. Bei nicht-verschwindender Dämpfung kann (z.B. bei einem Federschwinger) die Anregungsfrequenz zum Erreichen einer maximale Amplitude (Amplitudenresonanz) unterhalb der Eigenfrequenz der ungedämpften Schwingung liegen.
Die maximale Leistungsaufnahme (Leistungsresonanz) wird aber wirklich bei Anregung mit der ungedämpften Eigenfrequenz erreicht. Dort ist die Phasenverschiebung die sich einstellt auch entsprechend pi/2.
_________________
Formeln mit LaTeX |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 28. März 2009 09:32 Titel: schnudl Verfasst am: 28. März 2009 09:32 Titel: |
 |
|
das ist natürlich richtig, ich habe daher oben geschrieben:
| Zitat: | ...
Normalerweise ist die Resonanzfrequenz sehr nahe bei der Eigenfrequenz.
... |
Hier sind streng genommen drei Frequenzen zu unterscheiden:
1)
Eigenfrequenz des ungedämpften Schwingers:
Hier ist die Phase -90°.
Im Applet wird das als w0 bezeichnet.
2)
Eigenfrequenz des gedämpften Schwingers.
Das ist etwas kleiner als bei 1)
3)
Frequenz wo der Amplitudengang maximal wird.
Alle drei sind i.A. verschieden, liegen aber sehr nahe beisammen, wenn die Dämpfung ausreichend klein ist.
Trotzdem schwingt das System immer mit der Anregungsfrequenz, vorausgesetzt die freie Schwingung ist bereits abgeklungen. Davon wird aber ausgegangen, da der eingeschwungene Fall betrachtet wird.
Regt man mit f0 an, dann ist die Phase eben -90°. Sie stellt sich automatisch ein. Wo ist jetzt eigentlich das Problem?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 28. März 2009 10:24 Titel: para Verfasst am: 28. März 2009 10:24 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | | Regt man mit f0 an, dann ist die Phase eben -90°. Sie stellt sich automatisch ein. Wo ist jetzt eigentlich das Problem? |
Es gibt keins (hoffe ich). Ich wollte nur noch einmal darauf hinweisen, dass Alex' drittes Zitat aus dem Buch nicht ganz exakt (oder nicht exakt wiedergegeben) war.
Mit deiner übersichtlichen Gegenüberstellung der verschiedenen Frequenzen und der verwendeten Begriffe sollte das jetzt aber vollständig geklärt sein. :)
_________________
Formeln mit LaTeX |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 28. März 2009 10:49 Titel: schnudl Verfasst am: 28. März 2009 10:49 Titel: |
 |
|
@para, die Frage war nicht an dich gerichtet, sondern an @_Alex_. Sein letzter Post klang irgendwie so skeptisch.

_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 28. März 2009 12:39 Titel: _-Alex-_ Verfasst am: 28. März 2009 12:39 Titel: |
 |
|
Aber so genau wir in dem Zitat, was ich genau aus dem Buch abgeschrieben habe:P nicht eingegangen oder? Weil so genau hör ich das jetzt zum ersten mal.
Und in diesem Beispiel liegen die so weit beieinander, dass man da den Resonanzfall schon hat, wenn die Frequenz von Erreger und Resonator gleich sind? 
Ist darum auch die Phasenverschiebung nie genau 0,5phi? Bei der Simulation jetzt.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 28. März 2009 20:04 Titel: schnudl Verfasst am: 28. März 2009 20:04 Titel: |
 |
|
Wenn du in der Simulation die rote Frequenz gleich der blauen (w0) machst, dann ist die Phase bis auf einen rechenbedingten Rundungsfehler 0.5 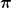 . Und man sieht auch, dass dort nicht das Amplitudenmaximum ist. . Und man sieht auch, dass dort nicht das Amplitudenmaximum ist.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 28. März 2009 22:35 Titel: _-Alex-_ Verfasst am: 28. März 2009 22:35 Titel: |
 |
|
Bei welcher Frequenz wäre es dann? Bei einer etwas kleineren, die man aber dort nicht genau einstellen kann?
Vermutlich liegt meine Verwirrung daran, dass wir in der Schule gesagt haben, dass wenn ein Schwinger gedämpft wird, seine Frequenz gleich bleibt. Und du hast ja eben gesagt, dass die des gedämpften etwas kleiner ist. Aber ich verstehe nicht wieso die Frequenz, bei der die Amplitude maximal wird, also ja dann der Resonanzfall, nicht genau die gleiche ist mit dem der Körper schwingt. Aber die hängen doch wenigstens zusammen oder? Also nicht so wie der eine gemeint hat, dass die Resonanzfrequenz völlig unabhängig von der Frequenz ist, mit der mein Körper schwingt?
Im Buch haben die als erstes dazu ein Beispiel gemacht, mit einem Wagen zwischen zwei Federn und einen einschaltbaren Motor. Dann haben sie den Wagen bei abgeschaltetem Motor einmalig ausgelenkt. Der Wagen schwang dann gedämpft mit der Frequenz f0. Dann haben die die Frequenz des Motor f verändert. Und als Ergebnis festgehalten, dass bei f=f0 der Resonanzfall ist. Da wurde dass dann doch auch nicht beachtet oder?
lg und danke schon mal für die tolle Hilfe 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 29. März 2009 09:40 Titel: schnudl Verfasst am: 29. März 2009 09:40 Titel: |
 |
|
| Zitat: | Vermutlich liegt meine Verwirrung daran, dass wir in der Schule gesagt haben, dass wenn ein Schwinger gedämpft wird, seine Frequenz gleich bleibt.
|
Das ist falsch, wenn es um die Frequenz der freien Schwingung geht. Denn diese wird definitiv kleiner, wenn das System bedämpft wird.
| Zitat: |
Bei welcher Frequenz wäre es dann? Bei einer etwas kleineren, die man aber dort nicht genau einstellen kann? |
Doch - mit den Einstellungen im Bild kannst du es deutlich sehen: Die 3.16... rad/s sind die Kreisfrequenz der freien ungedämpften Schwingung. Das wäre die Schwingungsfrequenz, wenn die Dämpfung Null ist. Ist diese aber grösser als Null, dann wird die Feder selbständig mit einer kleineren Frequenz schwingen, die man auch berechnen kann (aus m, C und D). Wird Die Dämpfung D immer grösser gemacht, dann wird die Feder irgendwann gar nicht mehr schwingen, sondern nach einem Exponentialgesetz die Ruheposition einnehmen. Diese Grenze nennet man den "aperiodischen Grenzfall" (du siehst das wenn du die Zahlen 10/1/4 für Federkonstante, Masse und Dämpfung sowie Frequenz=0 eingibst).
| Zitat: | | Aber ich verstehe nicht wieso die Frequenz, bei der die Amplitude maximal wird, also ja dann der Resonanzfall, nicht genau die gleiche ist mit dem der Körper frei schwingt. |
Warum sollte es so sein? Bei nicht zu grossen Dämpfungen stimmen diese Frequenzen aber gut überein.
Wichtig ist: Sobald du eine Schwingung erzwingst (z.B. durch hin- und her-bewegen des Aufhängepunktes) schwingt das System nach einiger Zeit nur noch mit dieser vorgegebenen Frequenz, und nicht mehr mit der Frequenz der freien, gedämpften Schwingung. Letztere ist nach einiger Zeit wegen der Dämpfung abgeklungen, und übrig bleibt nur die Antwort auf die vorgegebene Schwingung. Diese Antwort (=Amplitude+Phasenverschiebung) kann man auf Basis von m, C, D und w berechnen (siehe mein erster Post) und ist im Applet bei "Diagramm Amplitude" und "Diagramm Phasenunterschied" zu sehen.
| Beschreibung: |
|

Download |
| Dateiname: |
schwinger-1.png |
| Dateigröße: |
15.5 KB |
| Heruntergeladen: |
3583 mal |
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 29. März 2009 12:21 Titel: _-Alex-_ Verfasst am: 29. März 2009 12:21 Titel: |
 |
|
Danke:)
Bei deinen Einstellungen sieht man das in der Tat gut. Bei dem was ich mal probiert hab viel das eher weniger auf^^.
Aber ich finde blöd, dass das so in der Schule und in dem Buch nicht angesprochen wurde. Also angesprochen auf keinen Fall, und bei dem was in dem Buch steht, finde ich wird das nicht klar.
Ist es dann so, wie der eine gemeint hat, dass die Resonanzfrequenz völlig von der Frequenz w0 unabhängig ist? Weil ich hätte jetzt gedacht, dass die sich halt immer wie du gesagt hast ein wenig unterscheiden, aber wenn w0 größer wird, wird auch diese "Grenzfrequenz" größer.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 29. März 2009 16:26 Titel: schnudl Verfasst am: 29. März 2009 16:26 Titel: |
 |
|
was ist unabhängig?
Alle drei Frequenzen, nämlich
* die Frequenz der freien ungedämpften Schwingung
* die Frequenz der gedämpften Schwingung
* und die Frequenz, wo der Amplitudengang maximal ist
hängen von Masse, Federkonstante und Dämpfung ab. Von nicht mehr und von nicht weniger.
Und ausserdem liegen diese drei Frequenzen sehr nahe beisammen, wenn die Dämpfung klein ist.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 29. März 2009 17:52 Titel: _-Alex-_ Verfasst am: 29. März 2009 17:52 Titel: |
 |
|
Wird dann die Frequenz, bei der die Amplitude maximal wird, nicht größer, wenn die anderen beiden größer werden?
Ich hab irgendwie immer das Beispiel vor Augen, bei dem die sich im Buch überlegt haben, wie sie ein Pendel, das nach links und rechts schwingt, anregen müssen, damit die Auslenkung maximal wird. Und diese Bewegung muss ich doch immer schneller machen, je schneller mein Körper hin und her baumelt. 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 29. März 2009 19:52 Titel: schnudl Verfasst am: 29. März 2009 19:52 Titel: |
 |
|
ja, ich sagte ja, dass die drei Frequenzen meist (=kleine Dämpfung) nahe zusammen liegen (u.U. so nahe, dass du sie auf einem Bild nicht mehr unterscheiden kannst). Wird eine Frequenz grösser (z.B. weil die Federkonstante grösser wird), dann auch die beiden anderen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
_-Alex-_
Anmeldungsdatum: 06.03.2007
Beiträge: 262
|
 _-Alex-_ Verfasst am: 29. März 2009 20:06 Titel: _-Alex-_ Verfasst am: 29. März 2009 20:06 Titel: |
 |
|
Ah okay:) Wenn sich alle ändern, dann passt das ja.
Mich hat nur verwirrt dabei, dass einer halt behauptet hat, dass netmal das passieren würde.
Also vielen Dank 
|
|
 |
Romeo

Anmeldungsdatum: 27.02.2008
Beiträge: 148
|
 Romeo Verfasst am: 30. März 2009 17:14 Titel: Romeo Verfasst am: 30. März 2009 17:14 Titel: |
 |
|
Bevor ich ein neues Thema erstelle, stelle ich meine Frage hier einfach mit mit dazu - hoffe das ist ok!
Angenommen ich habe einen Serienschwingkreis bestehend aus einem Widerstand R, einer Spule L und einem Kondersator C, welche in Reihe an eine Wechselspannungsquelle geschaltet sind. Jetzt meine Frage: Ich hab gelesen, dass man in einer solchen Konstellation drei Resonanzfrequenzen definieren kann. Ich kenne konkret nur die eine, bei der der Imaginärteil der Impedanz zu Null wird - also maximale Spannung am Widerstand.
In diesem Fall:

Die anderen beiden sind so dargestellt, dass entweder die Spannung an der Induktivität oder an der Kapazität maximal sein soll. Dazu soll es was mit der Güte zutun haben. Angeblich sollen die drei Resonanzfrequenzen aber nahe beieinander liegen.
Die Güte in diesem Fall lautet:

Könnte mir das vielleicht jemand erklären? 
_________________
Grüße Romeo |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 30. März 2009 17:52 Titel: schnudl Verfasst am: 30. März 2009 17:52 Titel: |
 |
|
Versuch doch mal analytisch herauszufinden, wo die Spannung an L maximal wird. Dann kannst du dir den Zusammenhang zwischen "dieser" und der "ersten" Resonanzfrequenz selbst herleiten.
Tip: setze
 = 0)
Ist eine gute Übung 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Romeo

Anmeldungsdatum: 27.02.2008
Beiträge: 148
|
 Romeo Verfasst am: 30. März 2009 18:43 Titel: Romeo Verfasst am: 30. März 2009 18:43 Titel: |
 |
|
Ok, über Spannungsteiler ergibt sich:
^2}} \cdot |U_g|)
Für die Ableitung:
 http://img186.imageshack.us/img186/3180/rechnung.png http://img186.imageshack.us/img186/3180/rechnung.png
Damit ergibt sich für die Frequenz:

^2}})
Das sind meine errechneten Werte, mein Programm sagt noch zusätzlich plus und minus Unendlich.
Und das sollen jetzt die Resonanzfrequenzen sein, bei dem die Spannung an der Spule maximal sein wird. Ich denke mal für den Kondensator ist es Analog, nur eine andere Ableitung.
Aber wie hängt das nun mit der Güte zusammen? 
_________________
Grüße Romeo |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 30. März 2009 19:32 Titel: schnudl Verfasst am: 30. März 2009 19:32 Titel: |
 |
|

(obwohl man für eine solche Ableitung eigentlich kein Werkzeug benötigt...)
Zur Güte:
Du schriebst

Rechne daraus R aus und setze es in die von dir ermittelte Bestimmungsleichung für  ein! ein!
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Romeo

Anmeldungsdatum: 27.02.2008
Beiträge: 148
|
 Romeo Verfasst am: 30. März 2009 19:47 Titel: Romeo Verfasst am: 30. März 2009 19:47 Titel: |
 |
|
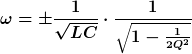
Ok, die Resonanzfrequenz hängt von der Qüte ab. Wenn die Güte gegen Unendlich läuft, habt man wieder die "normale" Resonanzfrequenz, sieht zumindest danach aus. Bei endlicher Güte gibt es also weitere Resonanzfrequenzen. Komisch... haben die einen teiferen Sinn? Wieso wird einen normalerweise nur die Resonanzfrequenz beigebracht bei der der Zweipol reell wird?
_________________
Grüße Romeo |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 30. März 2009 19:58 Titel: schnudl Verfasst am: 30. März 2009 19:58 Titel: |
 |
|
Es hängt davon ab, wie du "Resonanz" definierst. Hier steckt kein tieferer Sinn darin: andere Definition -> anderes Resultat
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Romeo

Anmeldungsdatum: 27.02.2008
Beiträge: 148
|
 Romeo Verfasst am: 30. März 2009 20:00 Titel: Romeo Verfasst am: 30. März 2009 20:00 Titel: |
 |
|
Ok, dann sag ich mal vielen Dank für die Herleitung und Erklärung! 
_________________
Grüße Romeo |
|
 |
Frage y0
Gast
|
 Frage y0 Verfasst am: 05. Apr 2009 18:38 Titel: Frage y0 Verfasst am: 05. Apr 2009 18:38 Titel: |
 |
|
Hallo schnudl!
Was bedeuten bitten in der Amplitudenformel die Größen C und D? Ich komme da mit den Einheiten nicht klar. Wieso ist Resonanz bei C - m w^2 = 0 und wieso folgt aus tan phi = + - oo phi = - 90° ?
mfG
Franz
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 06. Apr 2009 07:48 Titel: schnudl Verfasst am: 06. Apr 2009 07:48 Titel: |
 |
|
| Frage y0 hat Folgendes geschrieben: | Hallo schnudl!
Was bedeuten bitten in der Amplitudenformel die Größen C und D? Ich komme da mit den Einheiten nicht klar.
C ... Federkonstante N/m
D ... Dämpfungskonstante Ns/m
Wieso ist Resonanz bei C - m w^2 = 0 und wieso folgt aus tan phi = + - oo phi = - 90° ?
Wenn die Resonanz so definiert ist, dass der Imaginärteil verschwindet, dann kommtst du auf diese Bedingung. Ausserdem ist w²=C/m genau die Resonanzfrequenz des freien ungedämpften schwingers.
Und: Lass mal den Winkel von 0 auf -90° gehen und auch etwas drüber. Dann wirst du sehen, dass sich der Tangens so verhält.
mfG
Franz |
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Apr 2009 08:06 Titel: franz Verfasst am: 06. Apr 2009 08:06 Titel: |
 |
|
Hallo!
Beim Tangens hatte ich Klöße auf den Augen :-) . Klar und danke!
Laut Deiner Formel hat C dieselbe Einheit wie m w^2, also kg / s^2 und nicht N/m. Ähnlich D. Und alles zusammen müßte ja eine Länge werden.
Und wieso Resonanz bei C - m w^2 = 0 ?
mfG
Franz
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 06. Apr 2009 11:23 Titel: schnudl Verfasst am: 06. Apr 2009 11:23 Titel: |
 |
|
| franz hat Folgendes geschrieben: |
Laut Deiner Formel hat C dieselbe Einheit wie m w^2, also kg / s^2 und nicht N/m.
kgm/s² = N
also ist
kg/s² = N/m
Ähnlich D. Und alles zusammen müßte ja eine Länge werden.
Ich habe die Formel korrigiert:
 = \frac{F_0}{\sqrt{(C-m \omega^2 )^2+\omega^2 D^2}})
(--korrigiert-- ) )
statt
 = \frac{1}{\sqrt{(C-m \omega^2 )^2+\omega^2 D^2}})
Und wieso Resonanz bei C - m w^2 = 0 ?
Weil dort der Phasenwinkel -90° wird. Setze in meine Formel für die Phase ein!
mfG
Franz |
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Apr 2009 19:11 Titel: franz Verfasst am: 06. Apr 2009 19:11 Titel: |
 |
|
Hallo!
Als Resonanz würde ich (gefühlsmäßig) die Situation maximaler Amplitude ansehen, also yo'(w) = 0. Das dürfte aber eine andere Stelle sein.
mfG, F.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 06. Apr 2009 19:51 Titel: schnudl Verfasst am: 06. Apr 2009 19:51 Titel: |
 |
|
| franz hat Folgendes geschrieben: | Hallo!
Als Resonanz würde ich (gefühlsmäßig) die Situation maximaler Amplitude ansehen, also yo'(w) = 0. Das dürfte aber eine andere Stelle sein.
mfG, F. |
wir haben alleine in diesem Thread unzählige Male über dieses Thema diskutiert. Ich habe daher nun keine Lust mehr, noch irgend etwas darüber zu schreiben.. 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Apr 2009 21:36 Titel: franz Verfasst am: 06. Apr 2009 21:36 Titel: |
 |
|
Hallo schnudl,
es tur mit leid, wenn ich Dich langweile! Dein C hat jedoch immer noch nicht die versprochene Einheit N/m und das D nicht die Ns/m. Auch die Resonanz sehe ich anders (k Federkonstante, alpha Dämpfung).
Mit freundlichen Grüßen
Franz
| Beschreibung: |
|
| Dateigröße: |
4.28 KB |
| Angeschaut: |
6656 mal |
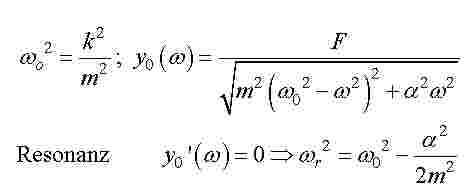
|
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 06. Apr 2009 22:21 Titel: schnudl Verfasst am: 06. Apr 2009 22:21 Titel: |
 |
|
| franz hat Folgendes geschrieben: | Hallo schnudl,
es tur mit leid, wenn ich Dich langweile! Dein C hat jedoch immer noch nicht die versprochene Einheit N/m
du sagst ja selbst, C hat laut meiner Gleichung die Einheit von mw², also ist dies

das ist gleichzeitig

und das D nicht die Ns/m.
Laut Gleichung hat mein wD die Einheit N/m, also

Wo hast du denn nun dein Problem ???Vielleicht bin ich betriebsblind, aber ....
Auch die Resonanz sehe ich anders (k Federkonstante, alpha Dämpfung).
Du kannst es gerne anders sehen; wir haben aber drei mögliche Definitionen von Resonanz weiter oben ausgiebigst diskutiert. Sogar deine Definition wurde dabei von @romeo im Detail vorgerechnet. Nun kommst du, und sagst, du siehst es anders, womit du die ganze bereits stattgefundene Diskussion von vorne losgehen lässt. Hast du diese gelesen?
Mit freundlichen Grüßen
Franz |
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
|


















 , darum weiß ich jetzt auch nicht wieso das so ist mit den Formeln.
, darum weiß ich jetzt auch nicht wieso das so ist mit den Formeln.
 . Jetzt steht ja doch bei dem dritten Punkt, dass im Resonanzfall f und f0 gleich sind. Also schon die Situation wie oben beschrieben herrschen muss? (Ich mach jetzt ein paar viele Fragezeichen hin:D weil ich mir echt net sicher bin:( ) Und dass im Resonanzfall eine Phasenverschiebung um phi/2 vorliegen muss.
. Jetzt steht ja doch bei dem dritten Punkt, dass im Resonanzfall f und f0 gleich sind. Also schon die Situation wie oben beschrieben herrschen muss? (Ich mach jetzt ein paar viele Fragezeichen hin:D weil ich mir echt net sicher bin:( ) Und dass im Resonanzfall eine Phasenverschiebung um phi/2 vorliegen muss.



 )
)