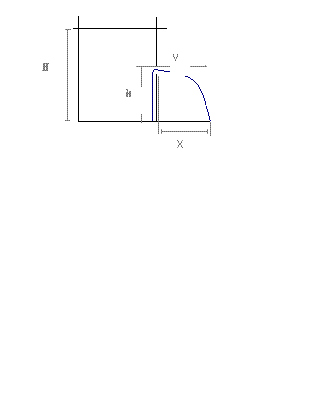
Maximale Reichweite eines Wasserstrahls

schrödingers_Kater · Anmeldungsdatum: 22.09.2010 Beiträge: 9

Hallo liebe Forum User,

Anhand er Skizze im Anhnag soll die Höhe h bei der X maximal wird bestimmt werden.

Mein Ansatz wäre:

1) Bernoulli-Gleichung:

2) Annahme zur Vereinfachung:

p0= p1= p(atomosphärisch) --> Der Druckterm fällt weg, da der Atmosphären Druck auf die Wasseroberfläche sowie auf den Wasserstrahl wirkt

Für die Höhe des Aussflusses setze ich an: z= H-h

Zur Bestimmung der maximalen Höhe müsste ich dann ableiten.

ABER: Wo bringe ich jetzt das X, also die Länge des Strahls unter? grübelnd

Den Rest krieg ich dann schon hin.
Vielen Dank.

GvC · Anmeldungsdatum: 07.05.2009 Beiträge: 14861

http://www.physikerboard.de/htopic,16599,wasserstrahl.html

Das einzige, was hier zu hinterfragen wäre, ist: Wieso kann die Austrittsgeschwindigkeit aus dem Energieerhaltungssatz hergeleitet werden?

schrödingers_Kater · Anmeldungsdatum: 22.09.2010 Beiträge: 9

Vielen Dank für den Link.

Ich habe gedacht dass man hier die Bernoulli-Gleichung in Form einer Energie-Gleichung ansetzt und dann so die maximale Reichweite ermittelt.

Aber der Ansatz mit der Wurfparabel leuchtet mir hier mehr ein!
(Manchmal hat man echt ein brett vorm Kopf!)

Vielen Dank! Thumbs up!

schrödingers_Kater · Anmeldungsdatum: 22.09.2010 Beiträge: 9

Aber die Berechnung mit Hilfe der Wurfparabel-Gleichung gilt nur, wenn man die Information mit dem Durchmesser außer acht lässt.

Was hat der Durchmesser des Aussflusses mit der maximalen Reichweite des Strahls zu tun?

Der beeinflusst doch nur den Wasserdruck. grübelnd

Deswegen war eigentlich mein erster Ansatz so gedacht:

Vereinfachung wie im 1. Post beschrieben

Tja, aber wie bringe ich jetzt die Fläche des Auslaufs

unter?

Oder ist die Angabe des Durchmessers nur zum verwirren?

Vielen dank.

GvC · Anmeldungsdatum: 07.05.2009 Beiträge: 14861

Irgendwie verstehe ich Deine Formel nicht. Da werden Geschwindigkeit und Druck addiert. Wie soll das denn gehen? Du kennst doch die Sache mit den Äpfeln und Birnen, die sich nicht addieren lassen.

Von der Querschnittsfläche des Loches war bislang gar nicht die Rede. Ich war deshalb auch nicht verwirrt. Die Fläche ist zur Lösung der gestellten Aufgabe auch nicht erforderlich, da ja nicht nach der Weite gefragt ist, sondern nur nach h für eine maximale Weite.

Dass v0 auch von der Querschnittsfläche abhängt, ist einzusehen. Insofern ist der Ansatz für zur Bestimmung von v0 in dem Link vermutlich nicht richtig. Aber darum geht es nicht. Es geht um die Bestimmung der Anfangsgeschwindigkeit in Abhängigkeit von (H-h). Wenn Du das raus hast, kannst Du v0 in die Wurfparabelgleichung einsetzen.

isi1 · Anmeldungsdatum: 03.09.2006 Beiträge: 2902 Wohnort: München

Ausflussgeschwindigkeit v = √ (2 g (H-h))

Zeit bis zum Boden: h = ½ g t² ---> t = √(2h/g)

Wurfweite: x = v t = √ ( 2 g (H-h) * 2h/g )

Maximum: dx/dh = 0 --> h = H/2

VeryApe · Anmeldungsdatum: 10.02.2008 Beiträge: 3247

der Durchmesser des Ausflusses hat insofern was mit der Ausflussgeschwindigkeit zu tun das je mehr ausfließt umso mehr sinkt auch das Behälterniveau.

Nun gehst du aber bei deiner Ausflussgeschwindigkeit von einen gleichbleibenden Behälterniveau aus. das gilt natürlich nur wenn die sinkgeschwindigkeit im Behälter vergleichweise gering ist.
Wenn also die Ausflussöffnung nicht sehr groß ist.

Warum spritzt aus einen engen Loch weiter als aus einen größeren=?

schon mal gefragt? Augenzwinkern

aber ich glaube nicht das du das hier berücksichtigen sollst.

isi1 · Anmeldungsdatum: 03.09.2006 Beiträge: 2902 Wohnort: München