| Autor |
Nachricht |
Daniel_HSE
Anmeldungsdatum: 01.04.2010
Beiträge: 29
|
 Daniel_HSE Verfasst am: 09. Apr 2010 18:20 Titel: Aus Kreuzprodukt r x F = M nach F auflösen Daniel_HSE Verfasst am: 09. Apr 2010 18:20 Titel: Aus Kreuzprodukt r x F = M nach F auflösen |
 |
|
Hey liebe Forumskollegen,
Ich hab mal ne Frage bzgl eines Kreuzproduktes hier speziell 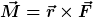 oder genauer im R³: oder genauer im R³:

Bei gegebenem Moment  und gegebenem Vektor und gegebenem Vektor 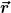 möchte ich nach der Kraft möchte ich nach der Kraft 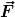 auflösen. auflösen.
Das bin ich auch schon angegangen und habe ein LGS aufgestellt:

Eigentlich müsste das doch eigentlich nach dieser Methode gehen, oder??
Leider ist jedoch die Determinante 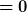 , was mir also sagt (und das sagt Excel und händische Rechnungen auch ), dass das LGS nicht lösbar ist. , was mir also sagt (und das sagt Excel und händische Rechnungen auch ), dass das LGS nicht lösbar ist.
Aber es muss doch möglich sein die Kraftkomponenten zu ermitteln....oder?
Ein herzliches Dankeschön, schonmal!!
Daniel |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 09. Apr 2010 18:26 Titel: pressure Verfasst am: 09. Apr 2010 18:26 Titel: |
 |
|
|
Nein, es gibt unendlich viele Kraftvektoren die ein gesuchtes Drehmoment bei vorgegebenen Hebelarm erzeugen können. Somit ist diese Gleichung bzw. die Operation Kreuzprodukt nicht umkehrbar, da sie nicht injektiv ist. Wenn du dir mal nur den Betrag von M anschaust, kannst du dies sofort sehen. |
|
 |
Daniel_HSE
Anmeldungsdatum: 01.04.2010
Beiträge: 29
|
 Daniel_HSE Verfasst am: 11. Apr 2010 16:57 Titel: Daniel_HSE Verfasst am: 11. Apr 2010 16:57 Titel: |
 |
|
Hey,
wie meinst du denn das mit dem Betrag von M? Irgendwie kann ich mir das noch nicht richtig vorstellen, mit diesen unendlich vielen Lösungen.
Wenn ich einen Hebelarm habe, und dessen verschiedene Komponente, dann müsste ich doch irgendwie die Kraftkomponente bestimmen können die zu den jeweiligen Hebelarmkomponenten gehören...so is jedenfalls mein Gefühl. Wenn ich das irgendwie lösen möchte, muss ich dann eine Komponente der Kraft vorgeben oder ähnliches?
Merci schonmal!
Daniel |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 11. Apr 2010 17:09 Titel: pressure Verfasst am: 11. Apr 2010 17:09 Titel: |
 |
|
Schauen wir uns doch mal das Kreuzprodukt genauer an:


Wobei Alpha der Winkel zwischen dem Vektor a und dem Vektor b ist. Ich will kurz einfach a und b schreiben.
Wenn a und b parallel oder antiparallel sind, dann wird das Kreuzprodukt 0. Somit kann man in diesem trivialen Fall nicht mehr von der Kenntnis von a auf b schließen, da es unendliche viele Vektoren gibt die parallel zu a sind.
Andernfalls spannen a und b immer eine Ebene auf und c steht immer senkrecht/normal auf dieser. Nun gibt es aber unendlich viele Vektoren die mit a dieselbe Ebene aufspannen und deren Betrag von Kreuzprodukt mit a gleich dem Betrag von c ist. Wenn b entsprechend kürzer ist als b' muss einfach der Winkel Alpha entsprechend angepasst werden.
Somit bilden mehre Vektoren das gleiche Kreuzprodukt mit a, damit kann mathematisch gesehen das Kreuzprodukt nie umgekehrt werden, da es nicht injektiv ist.
Wenn man das Kreuzprodukt umkehren könnte, warum hat dann noch niemand was von einer Kreuzdivision gehört ? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18071
|
 TomS Verfasst am: 11. Apr 2010 18:01 Titel: TomS Verfasst am: 11. Apr 2010 18:01 Titel: |
 |
|
Betrachten wir mal die Gleichung

Nun konstruieren wir eine Schar von Vektoren

Für alle diese Vektoren gilt
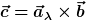
wegen
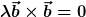
D.h. man kann zumindest fragen, wenn 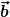 gegeben ist, ob man die Schar gegeben ist, ob man die Schar  konstruieren kann. konstruieren kann.
Außerdem könnte man eine Nebenbedingung fordern, z.B. dass der gesuchte Vektor senkrecht auf 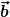 stehen soll: stehen soll:



Damit ist die Gleichung evtl. wieder eindeutig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Daniel_HSE
Anmeldungsdatum: 01.04.2010
Beiträge: 29
|
 Daniel_HSE Verfasst am: 13. Apr 2010 10:31 Titel: Daniel_HSE Verfasst am: 13. Apr 2010 10:31 Titel: |
 |
|
Vielen Dank für eure Antworten,
ich würde das mal zusammenfassend für mein Problem schreiben:
Also der Ansatz ist

mit

ist
)
und damit aufgelöst:

die Bedingung 
bringt mich dazu:
=0)
daraus:

ich müsste also ein LGS lösen, das hieraus entsteht:

Stimmt das so?
Das Ergebnis wäre dann eindeutig der Vektor 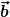 bzw. daraus der Vektor bzw. daraus der Vektor 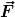 ? ?
Könnte, zumindest, wenn man es allgemein berechnen will kompliziert werden. Schon allein die Umstellung nach  , ,  und und  .... ....
Mein Texas Instruments Voyage200 steigt jedenfalls aus : /.
Vielen Dank und viele Grüße! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18071
|
 TomS Verfasst am: 13. Apr 2010 12:18 Titel: TomS Verfasst am: 13. Apr 2010 12:18 Titel: |
 |
|
Der Ansatz
| Daniel_HSE hat Folgendes geschrieben: |


|
enthält ein paar Unsauberkeiten bzgl. der Dimension der Argumente, da die Dimension vor r sicher nicht die einer Kraft ist.
Wenn du diesen Ansatz machst, dann setzt du doch voraus, dass r und b senkrecht zueinander sind, also

Damit ist
| Daniel_HSE hat Folgendes geschrieben: |
)
|
korrekt.
Die Bedingung
| Daniel_HSE hat Folgendes geschrieben: |

|
führt dann aber wegen

zu

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Daniel_HSE
Anmeldungsdatum: 01.04.2010
Beiträge: 29
|
 Daniel_HSE Verfasst am: 13. Apr 2010 12:46 Titel: Daniel_HSE Verfasst am: 13. Apr 2010 12:46 Titel: |
 |
|
Hm,
so ganz klar komme ich damit noch nicht.
1. Wie lässt sich denn das Dimensionsproblem lösen?
2. Ich kann also nicht nach  auflösen. Wie kann ich das denn jetzt lösen? Hast du denn evtl noch einen Ansatz für mich? Ich muss irgendwas noch festlegen um eine Lösung zu erzwingen, oder? Mit der Orthoginalität geht es ja scheinbar nicht? auflösen. Wie kann ich das denn jetzt lösen? Hast du denn evtl noch einen Ansatz für mich? Ich muss irgendwas noch festlegen um eine Lösung zu erzwingen, oder? Mit der Orthoginalität geht es ja scheinbar nicht? 
Danke! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18071
|
 TomS Verfasst am: 13. Apr 2010 14:10 Titel: TomS Verfasst am: 13. Apr 2010 14:10 Titel: |
 |
|
Korrektur: Deine Forderung

ist schon sinnvoll, aber nur, wenn du statt des (auch bzgl. der Dimension falschen) Ansatzes

und somit
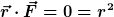
meinen Ansatz

und somit

forderst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Daniel_HSE
Anmeldungsdatum: 01.04.2010
Beiträge: 29
|
 Daniel_HSE Verfasst am: 13. Apr 2010 23:04 Titel: Daniel_HSE Verfasst am: 13. Apr 2010 23:04 Titel: |
 |
|
Hello TomS,
danke für deine Hilfe.
Ich muss mich erstmal mit Kugelkoordinaten auseinandersetzen, da das Neuland für mich ist.
Wenn ich ne Frage habe melde ich mich 
Bis dahin! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18071
|
 TomS Verfasst am: 13. Apr 2010 23:10 Titel: TomS Verfasst am: 13. Apr 2010 23:10 Titel: |
 |
|
Ich fasse mal meine Ideen zusammen.

Gesucht ist 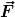
Nun mache ich den Ansatz

Dabei ist die Konstante des ersten Terms unbestimmbar; man kann sie also beliebig wählen (eine Forderung könnte sein, sie Null zu setzen).
Für den zweiten Term mache ich den Ansatz

Dies entspricht einem beliebigen Einheitsvektor, der senkrecht auf dem Ortsvektor steht.
Zunächst gilt
)
Damit folgt

also

mit

Im folgenden muss man die Identitäten für die Vektorprodukte der Einheitsvektoren in Polarkoordinaten ausnutzen.

Damit gilt


Setzt man dies alles in 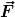 ein, so findet man ein, so findet man
\vec{e}_\theta + (\vec{e}_\theta\cdot\vec{M})\vec{e}_\phi])
Damit ist die Kraft bis auf den parallelen Anteil eindeutig bestimmbar, d.h. man erhält
\vec{e}_\theta + (\vec{e}_\theta\cdot\vec{M})\vec{e}_\phi])
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 14. Apr 2010 01:36 Titel: VeryApe Verfasst am: 14. Apr 2010 01:36 Titel: |
 |
|
Pff da wirds ja ziemlich kompliziert
Wie pressure schon geschrieben hat gibt es unendliche viele Lösungen.
Die einzige Sinnhafte Möglichkeit eine eindeutige Bestimmung zu erhalten ist, wenn man die Kraft normal auf den Hebelarm annimmt.
betrachtet man eine Kraft die normal auf den Hebelarm steht in einer Ebene.
Ich nehme die xy Ebene so gilt folgendes.




steht Fxy normal auf rxy so herrscht eine eindeutige Beziehung zwischen den 4 Komponenten nämlich folgende.
Der Beweis ist simple Mathematik sprich winkelgeometrie:


Bei bekannten R Vektor und M Vektor solltest du hiermit nun weiterkommen, wenn du alle 3 dimensionen so auflöst. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18071
|
 TomS Verfasst am: 14. Apr 2010 02:18 Titel: TomS Verfasst am: 14. Apr 2010 02:18 Titel: |
 |
|
Das ist zwar richtig, was wir da schreiben, aber wir stecken die Lösung schon in den Ansatz rein.
Betrachten wir also Orts- und Kraftvektor senkrecht aufeinander in der xy-Ebene; dann ist
 = r (a,b))
 = F (-b,a))
mit

Für das Vektorprodukt gilt dann
 \times (-b,a,0) = rF\,(0,0,1))
Das ist einsichtig, denn wir wir haben ja durch den Ansatz mittels xy-Ebene bereits festgelegt, dass

Damit ist

Nun müssen wir nur noch a und b durch die Ortskoordinaten ausdrücken


und erhalten unmittelbar die Komponenten der Kraft


also
)
Das ist nun lediglich ein Spezialfall der von mir o.g. Formeln, sowie die Darstellung in kartesischen statt in Polarkoordinaten.
Eigentlich ist es ja schon so, dass man ohne weitere Festlegungen keine Invertierung der Gleichung vornehmen kann; unter der Annahme weiterer Bedigungen steckt man aber quasi die Lösung schon in die Annahmen hinein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 14. Apr 2010 02:26 Titel: VeryApe Verfasst am: 14. Apr 2010 02:26 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Eigentlich ist es ja schon so, dass man ohne weitere Festlegungen keine Invertierung der Gleichung vornehmen kann; unter der Annahme weiterer Bedigungen steckt man aber quasi die Lösung schon in die Annahmen hinein.
|
Da hast du Recht, aber das liegt an der Definition von M Drehmoment.
Kraft mal Normalabstand.
Somit gehen sämtliche Informationen des Kraftanteils der nicht normal draufsteht verloren.
und sind nicht im Vektor M gespeichert.
Somit ist die einzige sinnvolle Annahme die oben geschilderte. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18071
|
 TomS Verfasst am: 14. Apr 2010 07:03 Titel: TomS Verfasst am: 14. Apr 2010 07:03 Titel: |
 |
|
Es gibt übrigens eine interessante Sache: Das Vektorprodukt in drei Dimensionen (und nur da existiert es!) ist eng verwand mit den sogenannten (vierdimensionalen) Quaternionen, einer Erweiterung der komplexen Zahlen. Für die Quaternionen existiert allerdings eine eindeutige Invertierung (wie oben diskutiert).
Etwas ähnliches wie das Vektorprodukt funktioniert noch in sieben Dimensionen, was mit der Existenz der (achtdimensionalen) Oktonionen zusammenhängt. Damit sind dann alle derartigen höherdimensionalen Strukturen aufgezählt: neben den reellen Zahlen existieren die "zweidimensionalen" komplexen Zahen (mit der Basis 1, i), die vierdimensionalen Quaternionen sowie die achtdimensionalen Oktonionen.
Andere algebraische Strukturen (sogenannte Divisionsalgebren) mit einer eindeutigen Umkehrbarkeit gibt es nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|

















