| Autor |
Nachricht |
Physiker567
Gast
|
 Physiker567 Verfasst am: 30. Apr 2019 19:15 Titel: Partielle Differentialgleichung mit Kreuzprodukt |
 |
|
Meine Frage:
Hallo, ich habe folgende partielle DGL die ich gerne lösen möchte:
 = \vec{A} \times \Delta \vec{A} )
Meine Ideen:
Zur Physik: Hinter dieser PDGL verbirgt sich ein klassisches Modell zur Beschreibung der Spindynamik auf einem Gitter im Heisenbergmodell. Sieht ein bisschen aus wie eine Diffusionsgleichung, aber ich komm irgendwie nicht weiter... |
|
 |
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 01. Mai 2019 00:24 Titel: |
|
|
|
Ich finde, Du könntest vielleicht etwas mehr erklären, worum es geht. Willst Du die Lösung in kartesischen oder Polarkoordinaten ? |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 01. Mai 2019 00:40 Titel: |
|
|
|
Wir freuen uns über Deine Lösung auagusti - egal in welchen Koordinaten! |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 01. Mai 2019 00:59 Titel: |
|
|
|
Jaja, das kann ich mir vorstellen, dann will ich aber auch einen Doktor in Mathematik dafür bekommen :-) |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
| jh8979 Verfasst am: 01. Mai 2019 15:46 Titel: |
|
|
|
Was soll denn ∆A sein? |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 02. Mai 2019 02:41 Titel: |
|
|
Delta A,
ist nicht erklärt,
ich geh davon aus, der Gast, der das hier reingesetzt hat und sich dann nicht drum kümmert, will uns veräppeln...
A ist ein zeitabhängiges Vektorfeld,
Delta ist der Lapplace Operator,
X ist das Kreuzprodukt von Vektoren
x ist eine Raumkoordinate
t soll die Zeitvariable sein.
Schleierhaft, was das Ganze soll. |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 02. Mai 2019 21:06 Titel: Re: Partielle Differentialgleichung mit Kreuzprodukt |
|
|
 = \frac{\partial \vec{A}(x,t)}{\partial t} &=& \vec{A}(x,t) \times \Delta A(x,t) \\&=& \vec{A}(x,t) \times div ( grad( A(x,t) ) ) \\&=& \vec{A}(x,t) \times div ( \begin{pmatrix} \frac{\partial }{\partial x} \\ \frac{\partial }{\partial y} \\ \frac{\partial }{\partial z} \end{pmatrix} A(x,t) ) ) )
mit  = |\vec{A}(x,t) |) Betrag des Vektors A(x,t), x = Länge in x-Richtung
Zuletzt bearbeitet von auagusti am 03. Mai 2019 11:36, insgesamt einmal bearbeitet |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 02. Mai 2019 21:28 Titel: Re: Partielle Differentialgleichung mit Kreuzprodukt |
|
|
off topic
Schön für Dich auagusti, daß Du Dich etwas mit den Grundbegriffen beschäftigst. Glaubst Du aber ernsthaft, daß das den Fragesteller weiterbringt? mfG! |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 02. Mai 2019 23:17 Titel: |
|
|
Ich grübel noch, was der Fragesteller gemeint hat. Eigentlich ist beim Thema Magnetismus im Festkörper die Wahl der Buchstaben etwas anders, also M für magnetisches Moment, H für Magnetfeldstärke, oder B für magnetische Induktion, S für Spinvektor, aber weißt Du jemanden der sich etwas besser auskennt, und der sagen kann, wofür da wohl der Buchstabe A... stehn könnten ?
Das würde weiterbringen. lg |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 03. Mai 2019 02:10 Titel: |
|
|
off topic
Hallo auagusti!
Ich schreibe Dir mal privat; das findet man unter "Im Forum stöbern / Neue Nachrichten". mfG! |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 03. Mai 2019 11:24 Titel: |
|
|
(off topic wg. franzs anfrage)
Hallo franz,
ich habe deine Nachricht gelesen, Du meinst, ein experte würde sich nicht an die Frage herantrauen ?
ich habe dir geantwortet, aber irgendwie ist die Nachricht nicht bei meinen gesendeten nahrichten aufgetaucht. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 03. Mai 2019 12:14 Titel: Re: Partielle Differentialgleichung mit Kreuzprodukt |
|
|
| auagusti hat Folgendes geschrieben: |
mit Betrag des Vektors A(x,t), x = Länge in x-Richtung |
Der Laplace-Operator ist auch für Vektorfelder definiert. Das Ergebnis ist ein Vektor (also der passende Operand für ein Kreuzprodukt  ). In der klassischen Vektoranalysis gilt die Identität
 - \nabla\times\nabla \times \vec{A},)
die als ad-hoc-Definition der linken Seite angesehen werden kann. Sowohl diese Identität als auch der klassische Laplaceoperator für Funktionen lassen sich systematisch als Spezialfälle des Laplace-de-Rham-Operators
auffassen, der für beliebige Differentialformen in euklidischen oder riemannschen Räumen erklärt ist.
(Zur Lösung der Gleichung kann ich aber leider gerade auch nichts beitragen.) |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 03. Mai 2019 13:07 Titel: |
|
|
offtopic - und Schluß
| auagusti hat Folgendes geschrieben: | | ich habe deine Nachricht gelesen, Du meinst, ein experte würde sich nicht an die Frage herantrauen ? |
Es war wohl ein Fehler, Dir vertrauensvoll zu schreiben: Eine persönliche Überlegung aus der Privatpost wird von Dir (vermutlich aus Dummheit) verfälscht und umgehend ans Schwarze Brett gepinnt.
 |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 03. Mai 2019 13:48 Titel: |
|
|
|
es tut mir leid, dass Du so ärgerlich bist. Ich habe aber nichts dergleichen gemacht, sondern nur eine Frage gestellt. |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 03. Mai 2019 13:58 Titel: Re: Partielle Differentialgleichung mit Kreuzprodukt |
|
|
| index_razor hat Folgendes geschrieben: |
(Zur Lösung der Gleichung kann ich aber leider gerade auch nichts beitragen.) |
Danke für den Hinweis, ich nahm an, es ist der Betrag gemeint.
ps. Ach so, jetzt kapier ich, Du meinst, es sei kein Vektor, aber es werde ein Vektor gebraucht, da stimme ich letzteres zu. |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 03. Mai 2019 14:23 Titel: |
|
|
 = \frac{\partial \vec{A}(x,t)}{\partial t} &=& \vec{A}(x,t) \times \Delta A(x,t) \\&=& \vec{A}(x,t) \times div ( grad( A(x,t) ) ) \\&=& \vec{A}(x,t) \times div ( \begin{pmatrix} \frac{\partial }{\partial x} \\ \frac{\partial }{\partial y} \\ \frac{\partial }{\partial z} \end{pmatrix} A(x,t) ) \\&=& \vec{A}(x,t) \times div ( \begin{pmatrix} \frac{\partial }{\partial x} A(x,t) \\ \frac{\partial }{\partial y} A(x,t) \\ \frac{\partial }{\partial z} A(x,t) \end{pmatrix} ) )
mit Betrag des Vektors A(x,t), x = Länge in x-Richtung |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18113
|
| TomS Verfasst am: 03. Mai 2019 14:36 Titel: Re: Partielle Differentialgleichung mit Kreuzprodukt |
|
|
Ich sehe nicht unmittelbar, wie man die nicht-lineare rechte Seite einfacher schreiben kann.
Evtl. kann man mittels der Identität
 - \nabla \times (\nabla \times A) )
etwas erreichen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 03. Mai 2019 14:59 Titel: Re: Partielle Differentialgleichung mit Kreuzprodukt |
|
|
| auagusti hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
(Zur Lösung der Gleichung kann ich aber leider gerade auch nichts beitragen.) |
Danke für den Hinweis, ich nahm an, es ist der Betrag gemeint.
ps. Ach so, jetzt kapier ich, Du meinst, es sei kein Vektor, aber es werde ein Vektor gebraucht, da stimme ich letzteres zu. |
Ich meine, daß du die Differentialgleichung wahrscheinlich falsch interpretierst. Es ist nicht die Anwendung des Laplace-Operators auf die Norm von 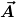 gemeint, was zusammen mit dem Kreuzprodukt im selben Term auch keinen Sinn ergäbe. Ich vermute stattdessen, daß der vektorielle Laplace-Operator gemeint ist, den ich oben definiert hatte. M.a.W. die Gleichung ergibt zumindest mathematisch Sinn, so wie sie ursprünglich da stand, deine Uminterpretation hingegen nicht. Ob sie physikalisch sinnvoll ist, kann ich nicht beurteilen, da ich sie zum ersten mal sehe. |
|
|
Physiker678
Gast
|
| Physiker678 Verfasst am: 03. Mai 2019 16:51 Titel: Re: PDGL |
|
|
Hier ist nochmal der Fragesteller!
Gemeint ist der vektorielle Laplace, d.h. in kartesischen Komponenten  . Ich habe auch bereits eine "Erhaltungsgröße" ausfindig gemacht, nämlich  . Könnte mir vllt. jemand eine mathematisch sinnvolle Antwort liefern? |
|
|
auagusti
Anmeldungsdatum: 28.04.2019
Beiträge: 36
|
| auagusti Verfasst am: 03. Mai 2019 16:55 Titel: |
|
|
| Physiker567 hat Folgendes geschrieben: | Meine Frage:
Hallo, ich habe folgende partielle DGL die ich gerne lösen möchte:
Meine Ideen:
Zur Physik: Hinter dieser PDGL verbirgt sich ein klassisches Modell zur Beschreibung der Spindynamik auf einem Gitter im Heisenbergmodell. Sieht ein bisschen aus wie eine Diffusionsgleichung, aber ich komm irgendwie nicht weiter... |
A(x,t) sei ein Vektor, dessen Länge von dem Ort x und der Zeit t abhängt.
A sei ein konstanter Vektor A
Dann ist mit Delta A = 0 und
 = A )
A(x,t) = A x t .
Vielen Dank für gute mathematische Unterstützung bei der Lösung, hätte nicht gedacht, daß es so simple ist. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18113
|
| TomS Verfasst am: 03. Mai 2019 17:11 Titel: Re: PDGL |
|
|
| Physiker678 hat Folgendes geschrieben: | Ich habe auch bereits eine "Erhaltungsgröße" ausfindig gemacht, nämlich
Könnte mir vllt. jemand eine mathematisch sinnvolle Antwort liefern? |
Kannst du zeigen, warum das eine Erhaltungsgröße ist?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18113
|
| TomS Verfasst am: 03. Mai 2019 17:14 Titel: |
|
|
| auagusti hat Folgendes geschrieben: | | Vielen Dank für gute mathematische Unterstützung bei der Lösung, hätte nicht gedacht, daß es so simple ist. |
Klingt irgendwie völlig falsch.
Kannst du mal bitte präzisieren, was "A x t" sein soll und wie das die o.g. Gleichung löst?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 03. Mai 2019 17:22 Titel: Re: PDGL |
|
|
| Physiker678 hat Folgendes geschrieben: | Hier ist nochmal der Fragesteller!
Gemeint ist der vektorielle Laplace, d.h. in kartesischen Komponenten . Ich habe auch bereits eine "Erhaltungsgröße" ausfindig gemacht, nämlich . |
Stimmt. Das bedeutet ein Vektor am festen Ort x wird lediglich einer zeitabhängigen Drehung unterworfen. Eine Lösung muß also die Bedingung
\times(\Delta\vec{A}(t, x)-\vec{\omega}(t, x))=0)
erfüllen, wobei 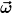 beliebig vorgegeben werden kann. Eine Klasse von Lösungen ergäbe sich also aus
=\vec{\omega}(t,x).)
und
Hilft das vielleicht schon weiter?
Zuletzt bearbeitet von index_razor am 03. Mai 2019 17:25, insgesamt einmal bearbeitet |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 03. Mai 2019 17:24 Titel: Re: PDGL |
|
|
| TomS hat Folgendes geschrieben: | | Physiker678 hat Folgendes geschrieben: | Ich habe auch bereits eine "Erhaltungsgröße" ausfindig gemacht, nämlich
Könnte mir vllt. jemand eine mathematisch sinnvolle Antwort liefern? |
Kannst du zeigen, warum das eine Erhaltungsgröße ist? |
Weil  laut rechter Seite ja senkrecht zu  steht, also ist
 |
|
|
Physiker678
Gast
|
| Physiker678 Verfasst am: 03. Mai 2019 17:34 Titel: Re: |
|
|
|
@index_razor, du hast die PDGL zu einem gekoppelten PDGL System gemacht, das bringt mich leider nicht weiter... |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 03. Mai 2019 17:38 Titel: Re: |
|
|
| Physiker678 hat Folgendes geschrieben: | | @index_razor, du hast die PDGL zu einem gekoppelten PDGL System gemacht, das bringt mich leider nicht weiter... |
Hast du das schon probiert? Die Lösung der Poisson-Gleichung kannst du explizit angeben. Dann bleibt eine gewöhnliche Differentialgleichung übrig. Kann natürlich sein, daß das zu nichts führt, aber versuchen würde ich es mal.
(Die Gleichungen sind übrigens nicht gekoppelt. Du suchst ja nicht  . Es sind einfach zwei Gleichungen für A.) |
|
|
|
Registrieren
Login
FAQ
Suchen
