| Autor |
Nachricht |
Tob23
Anmeldungsdatum: 13.01.2023
Beiträge: 1
|
 Tob23 Verfasst am: 13. Jan 2023 09:31 Titel: Partielle Ableitung vs. Totale Ableitung Tob23 Verfasst am: 13. Jan 2023 09:31 Titel: Partielle Ableitung vs. Totale Ableitung |
 |
|
Meine Frage:
Hallo,
ich habe gerade ein Logikproblem mit partiellen bzw. totalen Ableitungen:
Sei ,p(t),t) )
Dann gilt ja:

Somit ist  wenn F nicht explizit von t abhängt. wenn F nicht explizit von t abhängt.
Aber wenn man beispielsweise eine andere Funktion G in Abhängigkeit von Kugelkoordinaten hat gilt ja:

Aber nach der Logik von oben müsste diese partielle Ableitung doch einfach Null sein, da G nicht explizit von x abhängt sondern nur über die Verkettungen bzw. hat man hier doch quasi dann die totale Ableitung nach x vorliegen?
Wo ist mein Denkfehler?
Danke für die Hilfe im voraus!
Viele Grüße
Meine Ideen:
Ich hatte mir überlegt, dass man erstmal allgemein F(a,b,c) hat, dann die totale Ableitung bildet und dann erst q,p,t einsetzt, dann steht ja dasselbe da, jedoch ist die Schreibweise  dann immernoch etwas problematisch... dann immernoch etwas problematisch... |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 13. Jan 2023 13:04 Titel: Re: Partielle Ableitung vs. Totale Ableitung DrStupid Verfasst am: 13. Jan 2023 13:04 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| Tob23 hat Folgendes geschrieben: | Aber wenn man beispielsweise eine andere Funktion G in Abhängigkeit von Kugelkoordinaten hat gilt ja:
 |
Sicher? Das sieht mir eher nach der Ableitung

mit

aus. |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 13. Jan 2023 13:26 Titel: Re: Partielle Ableitung vs. Totale Ableitung Ich Verfasst am: 13. Jan 2023 13:26 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| Tob23 hat Folgendes geschrieben: |
Aber wenn man beispielsweise eine andere Funktion G in Abhängigkeit von Kugelkoordinaten hat gilt ja:
 |

EDIT: Überschneidung mit Dr. Stupid |
|
 |
Telefonmann
Anmeldungsdatum: 05.10.2011
Beiträge: 237
|
 Telefonmann Verfasst am: 13. Jan 2023 13:32 Titel: Re: Partielle Ableitung vs. Totale Ableitung Telefonmann Verfasst am: 13. Jan 2023 13:32 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| Tob23 hat Folgendes geschrieben: | Aber nach der Logik von oben müsste diese partielle Ableitung doch einfach Null sein, da G nicht explizit von x abhängt sondern nur über die Verkettungen bzw. hat man hier doch quasi dann die totale Ableitung nach x vorliegen?
Wo ist mein Denkfehler? |
Die fragliche Formel ist das Transformationsgesetz der partiellen Ableitungen.
Nimm ein Beispiel für G wo alle partiellen Ableitungen existieren und berechne sämtliche Ableitungen. Dann kannst die fragliche Formel überprüfen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 13. Jan 2023 14:18 Titel: Re: Partielle Ableitung vs. Totale Ableitung index_razor Verfasst am: 13. Jan 2023 14:18 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| Ich hat Folgendes geschrieben: | | Tob23 hat Folgendes geschrieben: |
Aber wenn man beispielsweise eine andere Funktion G in Abhängigkeit von Kugelkoordinaten hat gilt ja:
 |

|
G hängt vermutlich über  und und  auch noch von y und z ab. Deshalb wird man üblicherweise für die Ableitung der Verkettung nach x auch das Symbol auch noch von y und z ab. Deshalb wird man üblicherweise für die Ableitung der Verkettung nach x auch das Symbol  verwenden. Welches Symbol man für die Ableitung verwendet, ist hier aber vermutlich nicht das eigentliche Problem, sondern, daß das "G" auf der rechten Seite eine andere Funktion bezeichnet, als das "G" auf der linken Seite. Mit der partiellen Ableitung nach r ist die Ableitung der Funktion verwenden. Welches Symbol man für die Ableitung verwendet, ist hier aber vermutlich nicht das eigentliche Problem, sondern, daß das "G" auf der rechten Seite eine andere Funktion bezeichnet, als das "G" auf der linken Seite. Mit der partiellen Ableitung nach r ist die Ableitung der Funktion
)
bei fixen 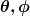 gemeint. (Für die partiellen Ableitung nach gemeint. (Für die partiellen Ableitung nach  gilt sinngemäß dasselbe.) Die partielle Ableitung nach x bezieht sich hingegen auf die Funktion gilt sinngemäß dasselbe.) Die partielle Ableitung nach x bezieht sich hingegen auf die Funktion
 = G(f(x,y,z), g(x,y,z), h(x,y,z)))
mit  = \sqrt{x^2 + y^2 + z^2}) etc. Und korrekt lautet die Formel etc. Und korrekt lautet die Formel

was nichts anderes als ein Spezialfall der Kettenregel ist. Nun gibt es natürlich keinen Grund anzunehmen, daß H (im Gegensatz zu G) nicht "explizit" von x abhängt.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 13. Jan 2023 14:32, insgesamt einmal bearbeitet |
|
 |
Telefonmann
Anmeldungsdatum: 05.10.2011
Beiträge: 237
|
 Telefonmann Verfasst am: 13. Jan 2023 14:27 Titel: Re: Partielle Ableitung vs. Totale Ableitung Telefonmann Verfasst am: 13. Jan 2023 14:27 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| index_razor hat Folgendes geschrieben: | G hängt vermutlich über  und und  auch noch von y und z ab. auch noch von y und z ab. |
Genau: Um diesen allgemeinen Fall zu berücksichtigen, wird die partielle Ableitung auf die totale Ableitung von G angewendet. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Jan 2023 09:52 Titel: Re: Partielle Ableitung vs. Totale Ableitung index_razor Verfasst am: 14. Jan 2023 09:52 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| Telefonmann hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | G hängt vermutlich über  und und  auch noch von y und z ab. auch noch von y und z ab. |
Genau: Um diesen allgemeinen Fall zu berücksichtigen, wird die partielle Ableitung auf die totale Ableitung von G angewendet. |
Ich verstehe zwar nicht, was das bedeuten soll. Aber ich denke, es gibt hier keine totale Ableitung von G. Unter der "totalen" Ableitung versteht man, denke ich, normalerweise die gewöhnliche Ableitung einer Verkettung
 = F(f(t), t)\qquad [F: \mathbb{R}^n\times \mathbb{R}\rightarrow \mathbb{R},\ f: \mathbb{R}\rightarrow \mathbb{R}^n]) , ,
d.h.
, t_0) \stackrel{\text{def}}{=} \lim_{t\to 0}\frac{1}{t}(H(t_0+t) - H(t_0))=H'(t_0).)
Die Transformation von G auf kartesische Koordinaten, , g(x,y,z), h(x,y,z))) hat aber nicht diese Form, d.h. es ist keine Funktion hat aber nicht diese Form, d.h. es ist keine Funktion  , sondern eine Funktion mehrerer Variablen , sondern eine Funktion mehrerer Variablen : \mathbb{R}^3\rightarrow\mathbb{R}) . .
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 14. Jan 2023 11:31 Titel: Re: Partielle Ableitung vs. Totale Ableitung Ich Verfasst am: 14. Jan 2023 11:31 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| index_razor hat Folgendes geschrieben: | Die Transformation von G auf kartesische Koordinaten, , g(x,y,z), h(x,y,z))) hat aber nicht diese Form, d.h. es ist keine Funktion hat aber nicht diese Form, d.h. es ist keine Funktion  , sondern eine Funktion mehrerer Variablen , sondern eine Funktion mehrerer Variablen : \mathbb{R}^3\rightarrow\mathbb{R}) . . |
Das ist doch dann genau ein Fall für das totale Differential. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Jan 2023 14:09 Titel: Re: Partielle Ableitung vs. Totale Ableitung index_razor Verfasst am: 14. Jan 2023 14:09 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| Ich hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Die Transformation von G auf kartesische Koordinaten, , g(x,y,z), h(x,y,z))) hat aber nicht diese Form, d.h. es ist keine Funktion hat aber nicht diese Form, d.h. es ist keine Funktion  , sondern eine Funktion mehrerer Variablen , sondern eine Funktion mehrerer Variablen : \mathbb{R}^3\rightarrow\mathbb{R}) . . |
Das ist doch dann genau ein Fall für das totale Differential. |
Ja, aber ich denke das ist nicht worum es in der Frage geht. Dort geht es vermutlich um die Anwendung der Kettenregel auf die partielle Ableitung der Funktion ) nach x. nach x.
Das "totale Differential" von 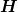 ist wiederum nichts anderes als die gewöhnliche Ableitung von H, in diesem Fall auch "Gradient" ist wiederum nichts anderes als die gewöhnliche Ableitung von H, in diesem Fall auch "Gradient"  genannt. (Man kann noch zwischen Vektor (Gradient) und Kovektor (Differential) unterscheiden, aber da wir vom genannt. (Man kann noch zwischen Vektor (Gradient) und Kovektor (Differential) unterscheiden, aber da wir vom 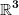 reden, bringt das nicht viel.) Tatsächlich sind alle diese "totalen" Ableitungen nur gewöhnliche Ableitungen einer Verkettung von Funktionen mittels Kettenregel ausgeschrieben. Das ist also eher ein Sprechweise, als ein fundamentales Konzept. (Das fundamentale Konzept ist die gewöhnliche Ableitung.) reden, bringt das nicht viel.) Tatsächlich sind alle diese "totalen" Ableitungen nur gewöhnliche Ableitungen einer Verkettung von Funktionen mittels Kettenregel ausgeschrieben. Das ist also eher ein Sprechweise, als ein fundamentales Konzept. (Das fundamentale Konzept ist die gewöhnliche Ableitung.)
Die partielle Ableitung ist hingegen eine spezielle Form der Richtungsableitung
 = \lim_{t\to 0}\frac{1}{t}(F(x+\vec{n}t) - F(x)),)
und der Unterschied zwischen gewöhnlicher Ableitung und Richtungsableitung ist der einzige, auf den es m.E. hier ankommt. (Es könnte z.B. die Größe  im Ausgangsbeitrag definiert sein, ohne daß die Ableitung im Ausgangsbeitrag definiert sein, ohne daß die Ableitung  existiert.) existiert.)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 851
|
 Qubit Verfasst am: 14. Jan 2023 22:47 Titel: Re: Partielle Ableitung vs. Totale Ableitung Qubit Verfasst am: 14. Jan 2023 22:47 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| index_razor hat Folgendes geschrieben: |
Das "totale Differential" von 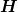 ist wiederum nichts anderes als die gewöhnliche Ableitung von H, in diesem Fall auch "Gradient" ist wiederum nichts anderes als die gewöhnliche Ableitung von H, in diesem Fall auch "Gradient"  genannt. (Man kann noch zwischen Vektor (Gradient) und Kovektor (Differential) unterscheiden, aber da wir vom genannt. (Man kann noch zwischen Vektor (Gradient) und Kovektor (Differential) unterscheiden, aber da wir vom 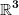 reden, bringt das nicht viel.) reden, bringt das nicht viel.) |
Im einfachsten Falle kann man auch vom totalen Differential einer Funktion f(x,y,z,..) sprechen, wenn gilt:
 = \alpha_x \, dx + \alpha_y \, dy + \alpha_z \, dz + ...)
mit
}{\partial x} \,, \alpha_y = \frac{\partial f(x,y,z,..)}{\partial y} \,, \alpha_z = \frac{\partial f(x,y,z,..)}{\partial z} \,, ..) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 15. Jan 2023 09:04 Titel: Re: Partielle Ableitung vs. Totale Ableitung index_razor Verfasst am: 15. Jan 2023 09:04 Titel: Re: Partielle Ableitung vs. Totale Ableitung |
 |
|
| Qubit hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Das "totale Differential" von 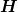 ist wiederum nichts anderes als die gewöhnliche Ableitung von H, in diesem Fall auch "Gradient" ist wiederum nichts anderes als die gewöhnliche Ableitung von H, in diesem Fall auch "Gradient"  genannt. (Man kann noch zwischen Vektor (Gradient) und Kovektor (Differential) unterscheiden, aber da wir vom genannt. (Man kann noch zwischen Vektor (Gradient) und Kovektor (Differential) unterscheiden, aber da wir vom 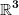 reden, bringt das nicht viel.) reden, bringt das nicht viel.) |
Im einfachsten Falle kann man auch vom totalen Differential einer Funktion f(x,y,z,..) sprechen, wenn gilt:
 = \alpha_x \, dx + \alpha_y \, dy + \alpha_z \, dz + ...)
mit
}{\partial x} \,, \alpha_y = \frac{\partial f(x,y,z,..)}{\partial y} \,, \alpha_z = \frac{\partial f(x,y,z,..)}{\partial z} \,, ..) |
Ja, das ist genau der Fall, von dem wir gerade sprachen. Das Differential von f an der Stelle x ist ein Kovektor, d.h. eine lineare Abbildung  : \mathbb{R}^n\rightarrow \mathbb{R}) mit der Eigenschaft mit der Eigenschaft
 = f(x) + \dd f(x)(\vec{v}) + O(\|\vec{v}\|^2)\qquad\text{(A)})
Der Gradient definiert genau dieselbe lineare Abbildung mittels Skalarprodukt  im im 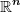
(\vec{v}) = \vec{\nabla} f(x)\cdot\vec{v}.)
Die Eigenschaft (A) bedeutet, daß ) die Funktion f an der Stelle x linear approximiert, was genau die definierende Eigenschaft der Ableitung ist, d.h. die Funktion f an der Stelle x linear approximiert, was genau die definierende Eigenschaft der Ableitung ist, d.h.
 = \text{Ableitung von f an der Stelle x},)
und im Fall der Existenz dieser Ableitung gilt auch
(\vec{e}_i) = \frac{\partial f(x)}{\partial x_i},)
was auf deine Formel für ) führt. führt.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
|















