| Autor |
Nachricht |
Vivien1987
Anmeldungsdatum: 25.05.2011
Beiträge: 1
|
 Vivien1987 Verfasst am: 25. Mai 2011 16:56 Titel: Geschwindigkeit ist die Ableitung des Ortes nach der Zeit ? |
 |
|
Meine Frage:
Hallo!
Ich studiere Biologie und habe jetzt den Kurs "Physik für Biologen" belegt. Ich habe ein paar grundsätzliche Fragen zur Mechanik und für Hilfe wäre ich sehr dankbar. Mein physikalisches Wissen ist leider stark beschränkt, ich hoffe auf Verständnis :-)
Ich habe mir die grundlegenden Formeln für gleichmäßige oder auch gleichmäßig beschleunigte Bewegungen angesehen, Übungsaufgaben gerechnet und es hat bestens funktioniert, trotzdem verstehe ich folgende Aussagen nicht wirklich:
Die Geschwindigkeit ist die Ableitung des Ortes nach der Zeit.
Die Beschleunigung ist die zeitliche Ableitung des Geschwin- digkeitsvektors oder die zweite zeitliche Ableitung des Ortsvektors.
... oder auch : die Ableitung der Orts- oder Weg-Zeit-Funktion nach der Zeit liefert die Momentangeschwindigkeit.....etc....
Ich musste bei meinen Übungsaufgaben weder abeleiten noch integrieren. Wann muss ich denn ableiten oder integrieren. Ich würde einfach gerne die Zusammenhänge verstehen. Könnte diese jemand anhand eines Beispiels/ einer Beispielrechnung erläutern,vorausgesetzt, dass es nicht zu viel Mühe macht? Vielleicht weiß auch jemand von euch, ob es online eine gute Quelle zum Verstehen gibt?
Ich bedanke mich und hoffe, dass sich niemand über solch banale Fragen ärgert, ich habe diese Frage bereits in einem anderen Forum gestellt und wurde nur beleidigt und angepöbelt und dann wurde der thread geschlossen...
Vielen Dank für eventuelle Hilfe
Vivien
Meine Ideen:
Ich habe im Buch vor mir gelesen:
...um vom s-t-Diagramm zum v-t Diagramm zum a-t-Diagramm zu gelangen, nehmen wir jeweils die zeitliche Ableitung. Ich habe gelesen, dass die erste Ableitung die Steigung der Kurve zum jeweiligen Zeitpunkt angibt, die zweite Ableitung die Krümmung. Trotzdem verstehe ich es nicht konkret.
Kann jemand von euch ein simples Beispiel angeben?
Gruß Vivien |
|
 |
Mkr
Anmeldungsdatum: 23.05.2011
Beiträge: 15
|
| Mkr Verfasst am: 25. Mai 2011 17:09 Titel: |
|
|
Nehmen wir:
=2t)
) ist hierbei die zurückgelegte Strecke zum Zeitpunkt  in einer beliebigen Längeneinheit.
gibt den Zeitpunkt an.
Nach  Zeiteinheiten befindet sich das Objekt beispielsweise also bei  längenheinheiten
Leitest du nun nach ab ergibt sich:
=v(t)=2)
) gibt die aktuelle Geschwindigkeit zum Zeitpunkt an. Daraus folgt, dass die Geschwindigkeit des Objektes, egal zu welchem Zeitpunkt, immer konstan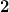t  ist.
Leitest du zweimal oder einmal nach ab ergibt sich:
=v'(t)=a(t)=0)
) ist die Beschleunigung am Zeitpunkt
Da die Geschwindigkeit ja bereits konstant war, ist es nur logisch, dass das Objekt nicht beschleunigt, denn sonst würde es ja mit der Zeit schneller werden.
War das Beispiel einfach genug? Hoffe, ich konnte dir ein wenig auf die Sprünge helfen.  |
|
|
Vivien_1987
Anmeldungsdatum: 25.05.2011
Beiträge: 3
|
| Vivien_1987 Verfasst am: 25. Mai 2011 17:27 Titel: |
|
|
Hallo Mkr!
Das war excellent und besser als jedes Buch! Vielen Dank!!! Ich habe es tatsächlich verstanden 
Kannst du das auch genauso fantastisch einfach für die Integralrechnung darstellen oder ist das komplizierter?
Grüße Vivien |
|
|
Mkr
Anmeldungsdatum: 23.05.2011
Beiträge: 15
|
| Mkr Verfasst am: 25. Mai 2011 17:38 Titel: |
|
|
Eigentlich ist es das Gleiche, nur andersherum. Gehen wir einfach wieder von der Geschwindigkeit =2) aus.
Nun wird integriert:
 \, \dd t = \int \! 2 \, \dd t = 2t = s(t))
Heißt, du bildest von der Geschwindigkeitsfunktion die Stammfunktion um die Funktion für die zurückgelegte Strecke zu erhalten.
Das ganze funktioniert auch so, wenn du zB. eine Beschleunigung hast.
Nehmen wir an ein Objekt wird mit =4) konstant beschleunigt.
Dann integrierst du:
 \, \dd t = \int \! 4 \, \dd t = 4t = v(t))
Und es resultiert die Geschwindigkeitsfunktion.
Dann nochmal integrieren:
 \, \dd t = \int \! 4t \, \dd t = 2t² = s(t))
Für dieses Objekt gelten also:
=2t²)
=4t)
Das ganze macht, wenn man es sich praktisch überlegt auch Sinn. Wenn das Objekt eine konstante Beschleunigung hast, wird die Geschwindigkeit mit der Zeit auch immer schneller und schneller. Und wenn es sich immer schneller Bewegt, so gelangt es auch schneller an weiter entfernte Orte. |
|
|
henry00
Anmeldungsdatum: 11.10.2010
Beiträge: 39
|
| henry00 Verfasst am: 25. Mai 2011 17:43 Titel: |
|
|
wichtig zu sagen ist noch, dass die Integralrechung ohne Anfangsbedinungen nicht eindeutig lösbar ist (im gegensatz zur Ableitung)
auch dieser Fakt ist leicht einsehbar.
Haben wir eine beschleunigung vorgegeben, zB a(t)=0, kann die Geschwindigkeit nicht eindeutig bestimmt werden. Denn ein Auto das konstant 70km/h fährt, und eines dass konstant 10km/h fährt hat in jedem Fall eine beschleunigung a(t)=0.
Also wenn du eine konkrete Integralrechung berechnen willst, brauchst du immer Anfangsbedingungen, und zwar für jedes weitere integral eine mehr.
Wenn du also die Beschleunigung vorgegeben hast, und du sollst denn weg bestimmen, führst du insgesamt 2 Integrale durch (a -> v -> x) und du brauchst daher 2 Anfangsbedingungen.
lg
Edit:
Somit wäre die Integralrechnung von Mkr streng genommen auch nicht ganz korrekt. Es müsste zB heissen:
 \, \dd t = \int \! 2 \, \dd t = 2t+c = s(t))
du hast also noch eine Konstante c, welche durch die Anfangsbedingung festgelegt wird.
Es könnte also beispielsweise in deiner Aufgabe vermerkt sein:
Anfangsbedingung: s(0)=0. Setzt du diese beziehung oben ein, erhältst du s(0)=0+c=0, also folgt, dass die Konstante c in diesem Fall 0 sein. |
|
|
Mkr
Anmeldungsdatum: 23.05.2011
Beiträge: 15
|
| Mkr Verfasst am: 25. Mai 2011 17:52 Titel: |
|
|
Das ist natürlich vollkommen korrekt. Ich hab es aber ausgelassen, weil es mir didaktisch nicht sinnvoll erscheint, jemandem, der Schwierigkeiten bei den Grundlagen hat, dirket einen Spezialfall zu nennen.
Aber henry hat schon recht, denn wenn du integrierst, gilt ja:
 \, \dd x = F(x)+C)
mit C als beliebige reelle Konstante.
Für das Modul Physik für Biologen aber vermutlich irrellevant, weil es sowieso jedes Thema der Experimentalphysik nur mal oberflächlich ankratzt. |
|
|
Vivien_1987
Anmeldungsdatum: 25.05.2011
Beiträge: 3
|
| Vivien_1987 Verfasst am: 25. Mai 2011 18:05 Titel: |
|
|
Hallo nochmal!
Vielen lieben dank für die wunderbare Erklärung. Ich wünsche mir, dass es auch in den Büchern so simpel dargestellt wird
Es ist schön, dass es leute wie dich gibt, die uns "doofen" so klasse helfen.
Danke nochmal und viele Grüße
Vivien |
|
|
Vivien_1987
Anmeldungsdatum: 25.05.2011
Beiträge: 3
|
| Vivien_1987 Verfasst am: 25. Mai 2011 18:19 Titel: |
|
|
Danke natürlich auch an Henry :thumbIch habe die neuen Beiträge jetzt erst gelesen!
Vielen dank euch beiden! |
|
|
henry00
Anmeldungsdatum: 11.10.2010
Beiträge: 39
|
| henry00 Verfasst am: 25. Mai 2011 18:39 Titel: |
|
|
| Mkr hat Folgendes geschrieben: | Das ist natürlich vollkommen korrekt. Ich hab es aber ausgelassen, weil es mir didaktisch nicht sinnvoll erscheint, jemandem, der Schwierigkeiten bei den Grundlagen hat, dirket einen Spezialfall zu nennen.
|
ja wir verstehen uns schon. Auch wenns vielleicht nicht oberste Priorität hat mit der "Uneindeutigkeit" des Integrals, ist dieser Fakt auch für Ahnungslose leicht und intuitiv einsehbar.
Ob man im Endeffekt gebrauch davon machen kann ist was anderes, aber zum grundsätzlichen Verständnis kann es sicher etwas beitragen  |
|
|
|
Registrieren
Login
FAQ
Suchen
