| Autor |
Nachricht |
Harald Arber
Gast
|
 Harald Arber Verfasst am: 22. Apr 2014 11:14 Titel: Lorentz vs. Zeit |
 |
|
|
Warum wird Lorentzkontraktion eines Körpers aufgehoben aber die Zeitdilatation nicht?
|
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 22. Apr 2014 11:25 Titel: |
|
|
Ich glaub Du musst etwas präzisieren was Du meinst:
Wann/Wo wird die Lorentzkontraktion denn "aufgehoben"?
|
|
|
Harald Arber
Gast
|
| Harald Arber Verfasst am: 22. Apr 2014 14:22 Titel: |
|
|
|
Lorentz: Ein Körper verkürzt sich und diese Verkürzung wird vollständig wieder aufgehoben. Zeit: Ein Körper altert langsamer, aber diese Alterung wird nicht aufgehoben oder rückgängig gemacht. Längenänderung wird aufgehoben, Zeitänderung nicht.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 22. Apr 2014 14:24 Titel: |
|
|
| Harald Arber hat Folgendes geschrieben: | | Lorentz: Ein Körper verkürzt sich und diese Verkürzung wird vollständig wieder aufgehoben. |
Wo/Wie wird die denn wieder aufgehoben?? Du musst Dich etwas verständlicher ausdrücken. Ich kann nur raten, was Du damit meinst...
|
|
|
-
Gast
|
| - Verfasst am: 22. Apr 2014 15:27 Titel: |
|
|
Vielleicht ist etwas in Anlehnung an das Zwillingsparadoxon gemeint? Am Ende, mit beiden Zwillingen in Ruhe relativ zueinander, wären diese gleich lang (bzw. breit), die Längenkontraktion ist gewissermaßen "aufgehoben". 
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 22. Apr 2014 15:50 Titel: |
|
|
|
Das Analogen zum Zwillingsparadoxon wäre, dass man sowas wie die Gesamtstrecke die zurückgelegt wird... und da hebt sich nichts auf: Für einen bewegten Beobachter ist die Strecke kürzer.
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 22. Apr 2014 16:49 Titel: |
|
|
Ich denke die Verkürzung der Strecke für bewegten Beobachter ist ein schwaches Argument da z. B. die Massenzunahme vollständig "aufgehoben" wird, nicht aber Lebensdauer eines bewegten Teilchen.
Die Frage finde ich schön!
"Zerfallszeiten von Teilchen und ihren Antiteilchen gleich sein müssen.
Eine Abweichung davon würde eine Verletzung der Lorentzinvarianz und somit der speziellen Relativitätstheorie zur Folge haben."
Was passiert wenn ein Teilchen(Myon) auf höhere Geschwindigkeit gebracht wird als sein ruhendes Antiteilchen?
"Das heißt, bewegte Myonen müssten eine längere Lebensdauer haben als ruhende."
Bedeutet das dass die Lorentzinvarianz verletzt wird?
Oder, dass die Schlussfolgerungen falsch sind und relativistisches Myon nur längere Strecke zurücklegen kann?
http://de.wikipedia.org/wiki/Zeitdilatation_bewegter_Teilchen
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
Harald Arber
Gast
|
| Harald Arber Verfasst am: 22. Apr 2014 16:56 Titel: |
|
|
| - hat Folgendes geschrieben: | | Vielleicht ist etwas in Anlehnung an das Zwillingsparadoxon gemeint? Am Ende, mit beiden Zwillingen in Ruhe relativ zueinander, wären diese gleich lang (bzw. breit), die Längenkontraktion ist gewissermaßen "aufgehoben". |
Ja, genau das meine ich, ein mit knapp c wegfliegender zwilling verkürzt sich, aber wenn er bei mir landet hat er wieder meine (erst ist ja mein Zwilling) originallänge. die zeit verkürzt/verlängert sich auch, aber dieser vorgang wird nicht rückgängig gemacht, der Zwilling kommt hat nicht mehr meine originalzeit.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 22. Apr 2014 17:04 Titel: |
|
|
|
Sobald der Zwilling wieder zurück ist, gehen auch beide Uhren wieder gleichschnell (d.h. Ticken gleichschnell)... nur die Gesamtzeit seit dem Start ist anders.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 22. Apr 2014 22:27 Titel: |
|
|
Lorentzkontraktion (allgemein Lorentztransformation) ist ein Effekt, wie ein ruhender Beobachter B einem relativ zu B bewegten Körper Länge (allgemein Koordinaten) zuschreibt, bzw. wie sich diese Länge (allgemein Koordinaten) bzgl. B in Abhängigkeit von der Bewegung ändern.
Zeitdilatation wird häufig ebenso dargestellt, das ist aber verwirrend.
Zeitdilatation kann verstanden und gemessen werden durch eine mit dem Körper mitbewegte Uhr und deren Zeit T' sowie durch eine bei dem ruhenden Beobachter B befindliche Uhr und deren Zeit T.
Lorentzkontraktion ist also ein "momentaner Scheineffekt", während Zeitdilatation verstanden werden kann als kumulativer Effekt entlang der Weltlinie eines Beobachters.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 22. Apr 2014 22:30 Titel: |
|
|
Genauso kann ich meinen gesamten Weg messen und vergleichen... so gesehen ist Lorentzkontraktion kein "Scheineffekt" (-> Warum kommen Myonen -in ihrem System betrachtet- auf der Erde an?)
Das Problem ist schlicht, dass der Fragesteller hier zwei Sachen vermischt: Lorentzkontraktion als lokalen (Raum-Zeit-)Effekt und Zeitdilatation als globalen gemessenen über einen endlichen Weg in der Raum-Zeit.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 22. Apr 2014 22:36 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | Genauso kann ich meinen gesamten Weg messen und vergleichen... so gesehen ist Lorentzkontraktion kein "Scheineffekt". |
Die Eigenzeit entlang eines Weges ist jedoch eine Invariante. Der Weg selbst jedoch nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 22. Apr 2014 22:52 Titel: |
|
|
Der Weg an sich nicht, Zeit an sich aber auch nicht.
Eigenzeit ist invariant, aber genauso ist der Weg zum selben Zeitpunkt invariant... und das ist was man miteinander vergleichen sollte, wenn man Zeitdilatation und Längenkontraktion vergleicht..
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 00:54 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | Eigenzeit ist invariant, aber genauso ist der Weg zum selben Zeitpunkt invariant... und das ist was man miteinander vergleichen sollte, wenn man Zeitdilatation und Längenkontraktion vergleicht.. |
Was ist der "Weg zum selben Zeitpunkt"?
Ich definiere die Eigenzeit als
Wie definierst du einen invarianten Weg?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 23. Apr 2014 00:57 Titel: |
|
|
|
"Weg(=Entfernung) zum selben Zeitpunkt" ist im Prinzip dasselbe wie "Zeit am selben Ort" (=Eigenzeit)... auch wenn man das so in der Regel nicht betrachtet. Mein Punkt: Im Prinzip ist das nicht viel anders und die behauptete Asymmetrie zwischen Lorentzkontraktion und Zeitdilatation ist einfach Blödsinn...
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 07:42 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | "Weg(=Entfernung) zum selben Zeitpunkt" ist im Prinzip dasselbe wie "Zeit am selben Ort" (=Eigenzeit)... auch wenn man das so in der Regel nicht betrachtet. Mein Punkt: Im Prinzip ist das nicht viel anders und die behauptete Asymmetrie zwischen Lorentzkontraktion und Zeitdilatation ist einfach Blödsinn... |
Ich versteh's nicht. Kannst du mal eine mathematische Definition hinschreiben, was du meinst?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
| bassiks Verfasst am: 23. Apr 2014 08:24 Titel: |
|
|
Ich stimme hier jh8979 zu. Was hier verglichen werden muss ist die Zeitdilatation mit der Lorentzkontraktion. Zwei Situationen:
1.) Während einer Relativbewegung: Der Beobachter sieht für den Reisenden die Zeit langsamer vergehen. Der Reisende nimmt eine Verkürzung der Strecke wahr. Es treten also Zeitdilatation und Lorentzkontraktion gemeinsam auf.
2.) Wenn sich beide treffen: Nun sind sie im selben Ruhesystem. Sie messen gleiche Entfernungen und die selbe Eigenzeit. Also keine Zeitdilatation und keine Lorentzkontraktion. Der Reisende behauptet er hätte eine kürzere Strecke zurückgelegt, der "ruhende" Beobachter behauptet nicht die Strecke wäre kürzer gewesen, sondern die Zeit wäre für den Reisenden langsamer vergangen. Beide Folgen sind also noch vorhanden, die Effekte selbst jedoch nicht mehr.
Ich sehe keinen Unterschied. Die Folge der Lorentzkontraktion ist genau so wenig "aufgehoben" wie die Folge der Zeitdilatation. Der Effekt selbst jedoch schon.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 08:55 Titel: |
|
|
| bassiks hat Folgendes geschrieben: | | Was hier verglichen werden muss ist die Zeitdilatation mit der Lorentzkontraktion. |
Ja.
| bassiks hat Folgendes geschrieben: | | 1.) Während einer Relativbewegung: Der Beobachter sieht für den Reisenden die Zeit langsamer vergehen. Der Reisende nimmt eine Verkürzung der Strecke wahr. Es treten also Zeitdilatation und Lorentzkontraktion gemeinsam auf. |
Wir sind uns einig, dass diese Effekte direkt aus der Lorentztransformation folgen, richtig? Demzufolge handelt es sich um Effekte aufgrund der aktuell ("jetzt") vorliegenden Relativgeschwindigkeit v.
| bassiks hat Folgendes geschrieben: | | 2.) Wenn sich beide treffen: Nun sind sie im selben Ruhesystem. Sie messen gleiche Entfernungen und die selbe Eigenzeit. |
Dies gilt aufgrund der aktuell verschwindenden Relativgeschwindigkeit.
| bassiks hat Folgendes geschrieben: | | Also keine Zeitdilatation und keine Lorentzkontraktion. Der Reisende behauptet er hätte eine kürzere Strecke zurückgelegt, der "ruhende" Beobachter behauptet nicht die Strecke wäre kürzer gewesen, sondern die Zeit wäre für den Reisenden langsamer vergangen. Beide Folgen sind also noch vorhanden, die Effekte selbst jedoch nicht mehr. |
Das sehe ich anders. Richtig ist, dass aktuell ("jetzt") keine Effekte mehr vorliegen, jedoch ein kumuliert Effekt über die gesamte Reise.
Man muss zwei Dinge unterscheiden:
A) Lorentztransformation sowie die daraus abgeleiteten Effekte der Längenkontraktion und der Zeitdilatation als "jetzt" vorliegende Effekte aufgrund einer "jetzt" (bzgl. t bzw. t' in S bzw. S') existierenden Relativgeschwindigkeit v. Diese Effekte werden mittels Koordinaten (t,x) bzw. (t',x') formuliert. Damit verschwinden die Effekte für v=0.
B) Zeitdilatation als kumulierter Effekt des Gangunterschiedes zweier Uhren entlang zweier Weltlinien. Dabei handelt es sich nicht um einen "jetzt" vorliegenden Effekt; und der Effekt kann (und muss) auch nicht mittels lokaler Koordinaten ausgedrückt werden, sondern mittels der Eigenzeiten, die i.A. gar keine Zeitkoordinate (im Sinne der SRT) definieren.
Ich habe die allgemeine Definitionsgleichung der Eigenzeit oben angegeben.
Die Zeitdilatation folgt als Differenz zweier Eigenzeiten.
Diese Definition ist koordinatenunabhängig, also invariant - im Gegensatz zu (A)
Ich kenne keine vergleichbare Definition einer invarianten Länge (genauer: raumartigen Strecke). D.h. ich kenne keine äquivalente Definition (und Messung) von Längenkontraktion. Wie misst das Myon die aus seiner Sicht verkürzte Strecke? Gibt es eine "Eigenlänge"?
Und deswegen sind für mich Längenkontraktion (als nicht direkt messbarer, Koordinatensystem-abhängiger Effekt) und Zeitdilatation (als physikalisch messbarer, Lorentzinvarianter Effekt) nicht äquivalent.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
| bassiks Verfasst am: 23. Apr 2014 09:02 Titel: |
|
|
| Zitat: | | Ich habe die allgemeine Definitionsgleichung der Eigenzeit oben angegeben. Die Zeitdilatation folgt als Differenz zweier Eigenzeiten. Diese Definition ist koordinatenunabhängig, also invariant - im Gegensatz zu (A) |
Das ist glaube ich der Punkt an dem wir aneinander vorbei reden. Für mich ist die Zeitdilatation der zuvor von dir erwähnte Effekt der nur während der Bewegung auftritt, also der Gangunterschied selbst. Das was du hier beschreibst, sofern ich dich richtig verstehe, ist für mich die Folge des Gangunterschieds. Dies ist für mich der Unterschied der vergangenen Eigenzeiten. Analog müsste ich statt der Lorentzkontraktion, welche nur während der Bewegung auftritt, den Unterschied der zurückgelegten Wege vergleichen. Dieser würde auch nachher bestehen.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 09:19 Titel: |
|
|
Wir reden nicht aneinander vorbei, wir haben nur eine unterschiedliche Meinung bzgl. der physikalischen Bedeutung der selben mathematischen Tatsachen. Klar, (A) handelt von raumzeitlich lokalen Effekten, (B) von kumulierten Effekten. Da sind wir uns einig.
Der wesentliche Punkt für mich ist, dass ich (B) für physikalisch primär halte, nicht jedoch (A). (B) handelt von einer physikalisch messbaren Invariante, (A) dagegen nicht.
Wenn du eine invariante, messbare Definition einer Eigenlänge angeben kannst, dann hast du mich überzeugt. Aber bisher sind die in (A) vorkommenden Größen nur indirekte, unbeobachtbare Hilfsgrößen. Primär und messbar ist dagegen der Laufzeitunterschied in (B).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
| bassiks Verfasst am: 23. Apr 2014 09:28 Titel: |
|
|
| Zitat: | | Wir reden nicht aneinander vorbei, wir haben nur eine unterschiedliche Meinung bzgl. der physikalischen Bedeutung der selben mathematischen Tatsachen. Klar, (A) handelt von raumzeitlich lokalen Effekten, (B) von kumulierten Effekten. Da sind wir uns einig. |
Ja da sind wir uns nun einig.
| Zitat: | | Der wesentliche Punkt für mich ist, dass ich (B) für physikalisch primär halte, nicht jedoch (A). |
Auch hier sind wir uns nun einig.
Du bezeichnest aber den Effekt des Gangunterschieds in A als Zeitdilatation und den daraus resultierenden Unterschied der vergangenen Zeit beim Vergleich der Uhren ebenfalls als Zeitdilatation. Ich bezeichne ersteres als Zeitdilatation und das ist wie du bereits geschrieben hast der Fall A und nicht primär.
Zu B: Wenn du nun also die vergangene Zeit vergleichst, so muss man meiner Meinung nach auch den zurückgelegten Weg vergleichen. Wenn nun der Reisende die Entfernung misst welche er zurücklegt und sie vergleicht mit der Entfernung die der Beobachter sieht, wird ebenfalls ein "kumullierter Effekt der Lorentzkontraktion" auftreten. Wie würde das Myon sonst erklären können warum es plötzlich an der Erdoberfläche ist?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 09:36 Titel: |
|
|
| bassiks hat Folgendes geschrieben: | | Wenn du nun also die vergangene Zeit vergleichst, so muss man meiner Meinung nach auch den zurückgelegten Weg vergleichen. Wenn nun der Reisende die Entfernung misst welche er zurücklegt und sie vergleicht mit der Entfernung die der Beobachter sieht, wird ebenfalls ein "kumullierter Effekt der Lorentzkontraktion" auftreten. |
Ich kann mich nur wiederholen:
Ich kenne keine vergleichbare Definition einer invarianten Länge (genauer: raumartigen Strecke). D.h. ich kenne keine äquivalente Definition (und Messung) von Längenkontraktion. Wie misst das Myon die aus seiner Sicht verkürzte Strecke? Gibt es eine "Eigenlänge"?
Wenn du eine invariante, messbare Definition einer Eigenlänge angeben kannst, dann hast du mich überzeugt.
| bassiks hat Folgendes geschrieben: | | Wie würde das Myon sonst erklären können warum es plötzlich an der Erdoberfläche ist? |
Das Myon erklärt das gar nicht. Für das Myon vergeht seine Eigenzeit, und da ist alles normal. Der Erklärungsbedarf tritt erst dann auf, wenn du einen anderen Beobachter einführst, der eine vom Myon abweichende Eigenzeit hat.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
| bassiks Verfasst am: 23. Apr 2014 10:49 Titel: |
|
|
| Zitat: |
Wie misst das Myon die aus seiner Sicht verkürzte Strecke? Gibt es eine "Eigenlänge"? |
Nein eine "Eigenlänge" kenne ich nicht. Warum willst du das unbedingt haben? Ein mitbewegter Beobachter misst keine Lorentzkontraktion, er misst aber auch keine Zeitdilatation. Was er misst ist die Eigenzeit. Auch die Zeitdilatation kommt nur zum Vorschein wenn man einen anderen Beobachter hinzu zieht. Dann kommt aber auch die Lorentzkontraktion hinzu. Am Beispiel des Myons:
Die Entfernung würde das Myon messen indem es misst wie lange die Erdoberfläche benötigt um bei ihm zu sein (Messung also in Eigenzeit, Myon betrachtet sich in Ruhe und die Erdoberfläche bewegt sich auf es zu). Die Entfernung ergibt sich dann über  . Das Myon spürt keine Zeitdilatation, es misst auch keine. Es misst nur die vergangene Eigenzeit. s ist aus seiner Sicht eben nur so lang. Für das Myon gibt es also keine Zeitdilatation und auch keine Lorentzkontraktion. Der Weg war einfach kurz genug dass es ihn vor dem Zerfall zurücklegen konnte.
Erst der Beobachter auf der Erde führt zur Erklärung mittels Zeitdilatation aus seiner Sicht. Das Myon kann sagen dass die Zeit ganz normal verlief, aber es einen anderen Weg wahrgenommen hat. Die Folge, nämlich das Myon ist auf der Erdoberfläche angekommen, ist die Selbe.
Ich sehe keinen Unterschied zwischen Lorentzkontraktion und Zeitdilatation.
Ich stimme dir aber zu dass ich eine Eigenzeit messen kann, aber eine Eigenlänge nicht.
Nochmal: Du musst deine Eigenzeiten auch erst vergleichen um eine Zeitdilatation zu erhalten. Ansonsten ist es für dich einfach nur die Eigenzeit. Auch die Länge muss erst verglichen werden. Ansonsten ist es eben einfach die Länge.
Ich denke auch hier haben wir das Problem zwischen uns. Die Lorentzkontraktion ist in gleichem Maße von der Eigenzeit abhängig wie die Zeitdilatation. Die Tatsache dass ich bei beiden die Eigenzeit benötige macht aber keines von beiden realer in meinen Augen.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 11:29 Titel: |
|
|
Dein Problem ist, dass du zwischen invarianten Beschreibungen mittels Eigenzeit und koordinatenabhängigen Beschreibungen, d.h. Lorentztransformation und Längenkontraktion, hin- und herwechselst.
Du kannst das auch für die Zeitdilatation tun, und dann erhältst du natürlich die Aussage, dass Längenkontraktion und Zeitdilatation, ausgedrückt durch Koordinatenzeiten, zwei Seiten der selben Medaille sind. Und in der SRT kannst du in Spezialfällen auch Eigenzeit mit Koordinatenzeit gleichsetzen. Im Myonexperimentes funktioniert das.
Im Allgemeinen funktioniert es jedoch nicht.
Betrachte einen ruhenden Beobachter B sowie in einem Ringbeschleuniger umlaufende Myonen als Beobachter B'. Die Myonen definieren kein IS, sie laufen auf einer Kreisbahn und können sich entlang dieser sogar mit variabler Geschwindigkeit bewegen. Der ruhende Beobachter kann den Umfang des Beschleunigers in seinem Ruhesystem messen sowie die gewohnte Formel für die Zeitdilatation verwenden. Für die Myonen funktioniert dies in Ermangelung eines IS nicht. M.E. steht dir die Argumentation mittels Längenkontraktion nicht zur Verfügung.
Der von mir oben skizzierte Weg für die Zeitdilatation funktioniert jedoch problemlos, wobei zur konkreten Berechnung ausschließlich auf das IS von B zurückgegriffen wird, in der allgemeinen Definition nicht mal auf das (die Definition ist koordinatenfrei).
D.h. dass der Zeitdilatation als messbarer Gangunterschied zweier Uhren = als Differenz zweier Eigenzeiten entlang zweier Weltlinien eine ausgezeichnete Bedeutung zukommt, die für eine räumliche Länge schlichtweg nicht existiert.
Dass Längenkontraktion und Zeitdilatation als zwei Seiten der selben Medaille wahrgenommen werden ist einigen Vereinfachungen geschuldet: Verwendung von Koordinaten statt Eigenzeiten, geradlinige und gleichförmige Bewegung, SRT statt ART.
Ich lasse mich aber gerne bekehren, wenn du eine äquivalente Formulierung mittels Längenkontraktion präsentierst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 23. Apr 2014 12:04 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Wenn du eine invariante, messbare Definition einer Eigenlänge angeben kannst, dann hast du mich überzeugt.
|
http://en.wikipedia.org/wiki/Proper_length
Ich weiss nicht so genau was Dich stört. Natürlich ist Eigenzeit ein sehr viel nützlicheres Objekt, als Eigenlänge. Aber man kann das alles analog definieren und analoge Größen betrachten... aber natürlich sind Zeitdilatation und Lorentzkontraktion verschiedene Dinge.
Mein Punkt am Anfang war nur, dass dort die zwei falschen Dinge verglichen wurden ("akkumuliert vs lokal"), aber da stimmen wir glaub ich alle überein.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 12:31 Titel: |
|
|
OK, damit könnte man versuchen, zu argumentieren. Da die Messung aber für zwei zeitartig voneinander getrennte Ereignisse stattfindet, sehe ich nicht sofort, wie man mit einem raumartigen Abstand weiterkommt.
Ich gebe dir aber recht, wir sind uns im wesentlichen einig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 23. Apr 2014 12:43 Titel: |
|
|
| TomS hat Folgendes geschrieben: | OK, damit könnte man versuchen, zu argumentieren. Da die Messung aber für zwei zeitartig voneinander getrennte Ereignisse stattfindet, sehe ich nicht sofort, wie man mit einem raumartigen Abstand weiterkommt.
|
In Deinem Myonenbeispiel?
Ich würde sagen einmal rechnet man es mit Deiner Formel um festzustellen wann die Myonen zerfallen (bzw die Hälfte zerfallen sind). Einmal rechnet man den Weg im Myonensystem aus, den die Myonen bis dahin zurückgelegt haben (mit der "Eigenlänge").
Wenn man es richtig macht, sollten konsistente Ergebnisse rauskommen. Sprich: Im Laborsystem, dass die Myomen "länger leben" um die Strecke zurückzulegen, im Myonensystem, dass die Strecke "kürzer ist". Ich glaub nicht, dass da ein prinzipielles Problem auftritt.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 12:51 Titel: |
|
|
Du meinst man parametrisiert eine geeignete kreisförmige Bahnkurve der Myonen im Beschleuniger?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 23. Apr 2014 13:07 Titel: |
|
|
|
Ja, um auszurechnen wie weit das Myon denkt dass es fliegt... Ich weiss nicht ob das technisch aufwendiger ist, aber vom Prinzip her sollte das funktionieren.
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 23. Apr 2014 17:43 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | [Ich würde sagen einmal rechnet man es mit Deiner Formel um festzustellen wann die Myonen zerfallen (bzw die Hälfte zerfallen sind). |
Bevor ein Missverständnis entstanden ist.
Wenn wir 1000 ruhenden Myonen haben
"Ruhende Myonen haben eine mittlere Lebensdauer von ca.
τ = 2,2*10^-6 sek "
und 1000 relativistischen Myonen,
v =0,9998 c entspricht Zeitfaktor 50
http://www.gymnasium-pegnitz.de/assets/files/fachbereiche/Physik/ScriptJakob/Script11/11_3_2Relativitaetstheorie(10)/Arbeitsblaetter/Aufg_Myonen.pdf
Zum Zeitpunkt 0 haben wir 2000 Myonen.
Wie viel Myonen haben wir nach 2,2*10^-6 sek?
Ich behaupte es bleiben ziemlich genau 1000 Myonen übrig.
Gibt es andere Überlegungen?
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 17:56 Titel: |
|
|
| D2 hat Folgendes geschrieben: | "Ruhende Myonen haben eine mittlere Lebensdauer von ca.
τ = 2,2*10^-6 sek "
...
Zum Zeitpunkt 0 haben wir 2000 Myonen.
Wie viel Myonen haben wir nach 2,2*10^-6 sek?
Ich behaupte es bleiben ziemlich genau 1000 Myonen übrig.
Gibt es andere Überlegungen? |
Ja ;-)
Du verwechselst die mittlere Lebensdauer mit der Halbwertszeit.
Es gilt
 = N_0 \, e^{-t / \tau})
Wobei tau die mittlere Lebensdauer bezeichnet.
Andererseits ist
 = N_0 \, e^{-T_{1/2} / \tau} \stackrel{!}{=} \frac{N_0}{2} )
Also
D.h. nach der mittleren Lebensdauer sind nicht 50% der ursprüngliche Teilchen übrig!!
Aber darum geht es hier nicht; wir sind uns dazu völlig einig; es geht rein um eine Frage der Interpretation
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 23. Apr 2014 18:07 Titel: |
|
|
Hä? was denn nun? mal 1000 mal 2000? Du redest wirr...
| D2 hat Folgendes geschrieben: | | Wie viel Myonen haben wir nach 2,2*10^-6 sek? |
Welche Zeit ist das, in welchem Bezugssystem?
| D2 hat Folgendes geschrieben: | | Ich behaupte es bleiben ziemlich genau 1000 Myonen übrig. |
Nein, im Laborsystem, in dem sie sich bewegen (also nicht in ihrem Ruhesystem), sind deutlich mehr noch übrig!
Und weil Du immer nach Experimenten fragst: So etwas ist bei einem Beschleuniger-Experiment Alltag! Aber das mit den kosmischen Myonen war eben eines der ersten Experimente, die das gezeigt hatten und damit die SRT belegt und die nicht-RT-Physik widerlegt hatte.
Gruß
Marco
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 23. Apr 2014 18:24 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | D2 hat Folgendes geschrieben: | "Ruhende Myonen haben eine mittlere Lebensdauer von ca.
τ = 2,2*10^-6 sek "
...
Zum Zeitpunkt 0 haben wir 2000 Myonen.
Wie viel Myonen haben wir nach 2,2*10^-6 sek?
Ich behaupte es bleiben ziemlich genau 1000 Myonen übrig.
Gibt es andere Überlegungen? |
Ja ;-)
Du verwechselst die mittlere Lebensdauer mit der Halbwertszeit. (1)
D.h. nach der mittleren Lebensdauer sind nicht 50% der ursprüngliche Teilchen übrig!!
Aber darum geht es hier nicht; wir sind uns dazu völlig einig; es geht rein um eine Frage der Interpretation(2) |
1 - das habe ich hier entnommen
"Der Begriff Lebensdauer (oft auch mittlere Lebensdauer) kennzeichnet in der Physik die durchschnittliche „Lebenszeit“ der Mitglieder eines Ensembles identischer Objekte.. Manchmal – insbesondere auf dem Gebiet der Radioaktivität – wird statt der Lebensdauer die Halbwertszeit T_{1/2} verwendet, d. h. die Zeit, nach welcher die Hälfte des Ensembles noch vorhanden ist"
http://de.wikipedia.org/wiki/Lebensdauer_(Physik)
2- auch wenn die Halbwertszeit etwa 69 % der Lebensdauer beträgt
Es geht mehr als um die Interpretation, es geht darum ob die
Zwillinge(Myonen) die in Bewegung sind länger als in Ruhe leben oder nicht.
Ich persönlich sehe das Problem, das man relativistischen Myonen
längeren Lebensdauer zuschreibt UND dass für diese die Strecken die Myonen überwinden müssen kürzer erscheinen. Nicht aber beides gleichzeitig! Entweder oder.
So verschwinden kumulative Effekte, falls nur die Strecke sich verkürzt.
Aber ich kann mich auch irren.
Vielleicht sollte ich besser fragen, wie verhält sich die Anzahl ruhenden Myonen zu den beweglichen Myonen, mit 0,9998 c nach 2,2*10^-6 sek?
PS. Bezugsystem/ Uhren - ruhendes System.
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 23. Apr 2014 19:49 Titel: |
|
|
| D2 hat Folgendes geschrieben: | | Ich persönlich sehe das Problem, das man relativistischen Myonen längeren Lebensdauer zuschreibt UND dass für diese die Strecken die Myonen überwinden müssen kürzer erscheinen. Nicht aber beides gleichzeitig! Entweder oder. |
Es geht um zwei verschiedene Interpretation des Effektes aus zwei verschiedenen Blickwinkeln. Beide sind jeweils für sich richtig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 23. Apr 2014 21:16 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Dein Problem ist, dass du zwischen invarianten Beschreibungen mittels Eigenzeit und koordinatenabhängigen Beschreibungen, d.h. Lorentztransformation und Längenkontraktion, hin- und herwechselst.
Du kannst das auch für die Zeitdilatation tun, und dann erhältst du natürlich die Aussage, dass Längenkontraktion und Zeitdilatation, ausgedrückt durch Koordinatenzeiten, zwei Seiten der selben Medaille sind. Und in der SRT kannst du in Spezialfällen auch Eigenzeit mit Koordinatenzeit gleichsetzen. Im Myonexperimentes funktioniert das.
Im Allgemeinen funktioniert es jedoch nicht.
Betrachte einen ruhenden Beobachter B sowie in einem Ringbeschleuniger umlaufende Myonen als Beobachter B'. Die Myonen definieren kein IS, sie laufen auf einer Kreisbahn und können sich entlang dieser sogar mit variabler Geschwindigkeit bewegen. Der ruhende Beobachter kann den Umfang des Beschleunigers in seinem Ruhesystem messen sowie die gewohnte Formel für die Zeitdilatation verwenden. Für die Myonen funktioniert dies in Ermangelung eines IS nicht. M.E. steht dir die Argumentation mittels Längenkontraktion nicht zur Verfügung..
Es geht um zwei verschiedene Interpretation des Effektes aus zwei verschiedenen Blickwinkeln.
Beide sind jeweils für sich richtig. |
Ich versuche es anders.
Ruhender Beobachter wartet nach Erzeugung von 1000 relativistischen Myonen ( v = 0,9998 c) 2,2*10^-6 sek lang und zählt übriggebliebene Myonen. Diese Zahl vergleich er mit übriggebliebenen Kontrollmyonen die ganze Zeit ruhten.
Wird eine große Abweichung zwischen beiden Zahlen erwartet?
"Myonen können im Ringbeschleuniger 33 km zurücklegen"
Aber "leben" diese im Ruhesystem des Beobachters deswegen länger?
http://www.gymnasium-pegnitz.de/assets/files/fachbereiche/Physik/ScriptJakob/Script11/11_3_2Relativitaetstheorie(10)/Arbeitsblaetter/Aufg_Myonen.pdf
Es kann nur eine Antwort geben, oder?
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 25. Apr 2014 10:41 Titel: |
|
|
| as_string hat Folgendes geschrieben: | | D2 hat Folgendes geschrieben: |
| D2 hat Folgendes geschrieben: | | Wie viel Myonen haben wir nach 2,2*10^-6 sek? |
Welche Zeit ist das, in welchem Bezugssystem?
| D2 hat Folgendes geschrieben: | | Ich behaupte es bleiben ziemlich genau 1000 Myonen übrig. |
Nein, im Laborsystem, in dem sie sich bewegen (also nicht in ihrem Ruhesystem), sind deutlich mehr noch übrig!
Und weil Du immer nach Experimenten fragst: So etwas ist bei einem Beschleuniger-Experiment Alltag! Aber das mit den kosmischen Myonen war eben eines der ersten Experimente, die das gezeigt hatten und damit die SRT belegt und die nicht-RT-Physik widerlegt hatte. |
|
Hier sind ähnliche Experimente beschrieben
"Atmosphärische Tests
In S hat Myon-S' eine größere Lebensdauer als Myon-S. Somit hat Myon-S' genügend Zeit um die Ruhelänge der Atmosphärenschichten bis zur Erdoberfläche zu durchdringen.
In S' hat Myon-S eine größere Lebensdauer als Myon-S'. "
http://de.wikipedia.org/wiki/Zeitdilatation_bewegter_Teilchen
bzw.
http://de.wikipedia.org/wiki/Myon
Wir sprechen von kumulativen Effekten. Stell dir vor wir haben 2 Ringbeschleuniger die Myonen in entgegengesetzte Richtungen auf die Geschwindigkeit von 0,9998 c.
S- ist Ruhesystem der Erde
S' -Ringbeschleuniger im Uhrzeigersinn
S'' Ringbeschleuniger in gegen den Uhrzeigersinn
bringen.
Beobachtet wird die Zerfallsrate der Myonen anderer 2 Systemen nur aus eigenem System.
Aus Sicht S (Erde) ist Zerfallsrate der Myonen beider Beschleunigungsringe identisch da die Geschwindigkeitshöhen identisch sind und die Richtung keine große Rolle spielt. Einverstanden?
Diese Zerfallsrate in Beschleunigungsringen ist aber deutlich niedriger als im System(Erde) aus welchem beobachtet wird. Einverstanden?
Die relativistische Addition 0,9998c +0,9998c ergibt 0,99999998c
Das spielt aber keine große Rolle, da in anderen Systemen (auch auf der Erde) grundsätzlich Zerfallsraten niedriger sind als die eigene Zerfallsraten (aus Sicht des Myons welches in einem der Beschleunigungsringen befindet). Einverstanden?
Jeder Zerfall ist aber ein Ereignis was in allen anderen Systemen registriert werden kann. Einverstanden?
Wie kann es aber sein, dass jedes System weniger Zerfällen in anderen Systemen beobachten als in eigenem?
Ich hoffe ich könnte meine Frage so stellen, dass Widerspruch solchen Aussagen wie
"In S' hat Myon-S eine größere Lebensdauer als Myon-S'."
deutlich wird.
_________________
Lösungen gibt es immer, man muss nur darauf kommen.
Zuletzt bearbeitet von D2 am 25. Apr 2014 12:09, insgesamt einmal bearbeitet |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 25. Apr 2014 11:24 Titel: |
|
|
| D2 hat Folgendes geschrieben: | Beobachtet wird die Zerfallsrate der Myonen anderer 2 Systemen nur aus eigenem System.
Aus Sicht S (Erde) ist Zerfallsrate der Myonen beider Beschleunigungsringe identisch da die Geschwindigkeitshöhen identisch sind und die Richtung keine große Rolle spielt. Einverstanden? |
Ja
| D2 hat Folgendes geschrieben: | | Diese Zerfallsrate in Beschleunigungsringen ist aber deutlich niedriger als im System(Erde) aus welchem beobachtet wird. Einverstanden? |
Den Satz verstehe ich nicht. Die Zerfallsrate ist im System(Erde) niedriger als im System(Erde)???
| D2 hat Folgendes geschrieben: | | Die relativistische Addition 0,9998c +0,9998c ergibt 0,99999998c |
Mag sein, ich hab's nicht nachgerechnet. Der konkrete Wert spielt ja auch keine große Rolle. Wir sind uns einig: Die "Summe" liegt näher an c, als die einzelnen Geschwindigkeiten.
| D2 hat Folgendes geschrieben: | Das spielt aber keine große Rolle, da in anderen Systemen (auch auf der Erde) grundsätzlich Zerfallsraten niedriger sind als die eigene Zerfallsraten (aus Sicht des Myons welches in einem der Beschleunigungsringen befindet). Einverstanden?
Jeder Zerfall ist aber ein Ereignis was in allen anderen Systemen registriert werden kann. Einverstanden? |
Auch wenn ich den ersten Satz nicht verstehe, aber ich vermute mal, dass der zweite alles Gesagte zusammen fasst und damit bin ich einverstanden: Die Eigenzeit ist immer die kürzeste, die Zeit in allen dazu bewegten Bezugssystem ist länger, richtig.
| D2 hat Folgendes geschrieben: | | Wie kann es aber sein, dass jedes System weniger Zerfällen in anderen Systemen beobachten als in eigenem? |
Da wären wir wieder beim Zwillings-"Paradoxon"... Alles in den ellenlangen Threads dazu gesagte kannst Du auch hier anwenden.
Wenn Du keine absolute Zeit zugrunde legst, geht das ohne Problem. Das ist ja gerade der Witz.
Im Ruhesystem legt das Myon ja auch keine Strecke zurück, im Erdsystem aber schon. Wenn Du noch so Effekte wie Relativität der Gleichzeitigkeit berücksichtigst, geht das alles problemlos. Widerspricht eben nur unserer Denke, dass überall alle Uhren synchron gehen und es eine Zeit gibt, die über alles und für alle gleich sein müsse...
Gruß
Marco
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 25. Apr 2014 12:38 Titel: |
|
|
| as_string hat Folgendes geschrieben: | | D2 hat Folgendes geschrieben: | | Diese Zerfallsrate in Beschleunigungsringen ist aber deutlich niedriger als im System(Erde) aus welchem beobachtet wird. Einverstanden? |
Den Satz verstehe ich nicht. Die Zerfallsrate ist im System(Erde) niedriger als im System(Erde) |
Ich versuche es mit anderen Worten.
Im Ruhesystem Erde nach 2,2 *10^-6 s ist schon die Hälfte der ruhenden Myonen zerfallen, aber in Beschleunigungsringen existieren noch 99% aller Myonen aus Sicht des ruhenden Beobachters(Erde). | as_string hat Folgendes geschrieben: | | D2 hat Folgendes geschrieben: | ten Satz nicht verstehe, aber ich vermute mal, dass der zweite alles Gesagte zusammen fasst und damit bin ich einverstanden: Die Eigenzeit ist immer die kürzeste, die Zeit in allen dazu bewegten Bezugssystem ist länger, richtig. | D2 hat Folgendes geschrieben: | | Wie kann es aber sein, dass jedes System weniger Zerfällen in anderen Systemen beobachten als in eigenem? |
Da wären wir wieder beim Zwillings-"Paradoxon"... Alles in den ellenlangen Threads dazu gesagte kannst Du auch hier anwenden.
Wenn Du keine absolute Zeit zugrunde legst, geht das ohne Problem. Das ist ja gerade der Witz.
Im Ruhesystem legt das Myon ja auch keine Strecke zurück, im Erdsystem aber schon. Wenn Du noch so Effekte wie Relativität der Gleichzeitigkeit berücksichtigst, geht das alles problemlos. Widerspricht eben nur unserer Denke, dass überall alle Uhren synchron gehen und es eine Zeit gibt, die über alles und für alle gleich sein müsse... |
|
Ich habe Probleme mit Ereignissen die für alle Beobachter gelten.
Folgende Idee, da Myonen von einander nicht unterscheidbar sind aber trotzdem jeder eine laufende Nummer(z. B. gilt räumliche Anordnung/eine farbliche Zuordnung )bekommen kann, vergleichen wir die Aufzeichnungen alle Beobachter.
Wenn Myon Nummer 37 im Beschleunigungsring S' im roten Sektor zerfällt ,
dann ist diese Konstellation 37+rot für Beobachter S und Beobachter S''
bindend, einverstanden?
Ich schlage vor einzelne Myonen aus unterschiedlichen Bezugsystemen zu beobachten, ich hoffe dies ist legitim und sogar machbar!
So kann man vielleicht besser verstehen was eigentlich passiert.
PS.Das die Zwillinge asymmetrische Bedingungen haben stört mich wenig.
Das diese scheinbar kürzer werden mal mit Raum rum herum mal ohne, stört mich wenig.
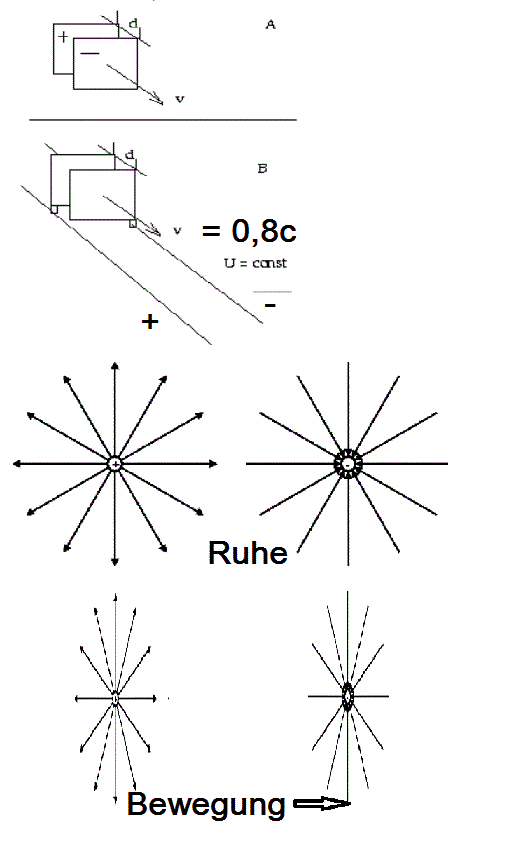
PPS. Ich habe kein Problem dass Kondensator kein Spannungsüberschlag bekommen wird egal ob Beobachter auf den geladenen Kondensator zufliegt oder ob dieser sich um auf 60% seiner Dielektrikum Dicke schrumpft, da seine Geschwindigkeit 0,8 c beträgt.
Ich habe kein Problem, da so einen Spannungsüberschlag kein Ereignis ist, weil dieser niemals stattfinden kann - ganz unten kann man sehen warum nicht.
Aber Zerfall eines Teilchen ist ein Ereignis! Da kann man die Augen nicht zudrücken und behaupten man hat diese nicht registriert, oder nicht so oft.
Kurz gesagt: Aus Sicht des bewegten Beobachters im Ring müssen die ruhenden Myonen auf der Erde schneller zerfallen und die Zerfallsrate im anderem Beschleunigungsring muss identisch eigener Zerfallsrate sein, unabhängig davon in welche Himmelsrichtung die Beschleunigungsringe ausgerichtet sind.
| Beschreibung: |
|
| Dateigröße: |
17.36 KB |
| Angeschaut: |
13132 mal |
|
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 25. Apr 2014 13:13 Titel: |
|
|
| D2 hat Folgendes geschrieben: | Ich versuche es mit anderen Worten.
Im Ruhesystem Erde nach 2,2 *10^-6 s ist schon die Hälfte der ruhenden Myonen zerfallen, |
Was meinst Du hier mit "Ruhesystem Erde"??? Es muss doch das Ruhesystem der Myonen sein. Du meinst also ein Myon, das auf der Erde ruht oder wie? Dann schreib doch einfach "Ruhesystem Myon" und nicht "Ruhesystem Erde"!
| D2 hat Folgendes geschrieben: | | aber in Beschleunigungsringen existieren noch 99% aller Myonen aus Sicht des ruhenden Beobachters(Erde). |
Jetzt hast Du schon wieder Ruhesystem Erde. Wenn Du zwei Bezugssysteme unterscheiden willst, dann ist es doch ungünstig, beide "Ruhesystem Erde" zu nennen.
Was Du doch sagen willst: Du betrachtest den Vorgang in einem Bezugssystem, in dem ein (eigentlich viele, weil man sonst von Wahrscheinlichkeiten reden müsste) Myon ruht. Und einmal betrachtest Du einen Vorgang (den selben?) aus einen Bezugssystem, in dem das Myon sich bewegt.
Wenn Du die Zeit misst (wie auch immer, das musst Du Dich auch mal genauer fragen: Im einen Fall findet der Zerfall an der selben Stelle statt, wie die Zeit auch losgelaufen ist (Myon in Ruhe), im anderen Fall ist es aber ein ganz anderer Ort und wir müssen die Einstein-Uhrensynchronisation und so weiter verwenden, um da überhaupt eine Zeit messen zu können!), dann sind die in den beiden Bezugssystemen unterschiedlich.
| D2 hat Folgendes geschrieben: | Folgende Idee, da Myonen von einander nicht unterscheidbar sind aber trotzdem jeder eine laufende Nummer(z. B. gilt räumliche Anordnung/eine farbliche Zuordnung )bekommen kann, vergleichen wir die Aufzeichnungen alle Beobachter.
Wenn Myon Nummer 37 im Beschleunigungsring S' im roten Sektor zerfällt ,
dann ist diese Konstellation 37+rot für Beobachter S und Beobachter S''
bindend, einverstanden?
Ich schlage vor einzelne Myonen aus unterschiedlichen Bezugsystemen zu beobachten, ich hoffe dies ist legitim und sogar machbar!
So kann man vielleicht besser verstehen was eigentlich passiert. |
Es ist ganz egal: Du kannst ein und denselben Vorgang aus einem beliebigen Bezugssystem beschreiben und wenn Du die RT korrekt anwendest, bekommst Du auch das selbe Ergebnis. Wenn das Myon im einen Bezugssystem im "roten Sektor" zerfällt, tut es das auch in allen anderen. Das ist bei der SRT schon auch genau so.
| D2 hat Folgendes geschrieben: | PS.Das die Zwillinge asymmetrische Bedingungen haben stört mich wenig.
Das diese scheinbar kürzer werden mal mit Raum rum herum mal ohne, stört mich wenig. |
Hä? Raum drum herum?
Ich hatte das eher anderes gemeint: Das Alter der Myonen ist unterschiedlich, wenn sie über unterschiedliche Wege durch die Raumzeit bewegt wurden.
Gruß
Marco
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 25. Apr 2014 13:49 Titel: |
|
|
| as_string hat Folgendes geschrieben: | Es ist ganz egal: Du kannst ein und denselben Vorgang aus einem beliebigen Bezugssystem beschreiben und wenn Du die RT korrekt anwendest, bekommst Du auch das selbe Ergebnis. Wenn das Myon im einen Bezugssystem im "roten Sektor" zerfällt, tut es das auch in allen anderen. Das ist bei der SRT schon auch genau so.
| D2 hat Folgendes geschrieben: | PS.Das die Zwillinge asymmetrische Bedingungen haben stört mich wenig.
Das diese scheinbar kürzer werden mal mit Raum rum herum mal ohne, stört mich wenig. |
Hä? Raum drum herum?
Ich hatte das eher anderes gemeint: Das Alter der Myonen ist unterschiedlich, wenn sie über unterschiedliche Wege durch die Raumzeit bewegt wurden.
|
Wegen "Raum drum herum" habe ich folgendes gemeint.
Für ruhenden Beobachter verkürzen sich die bewegliche Objekte, für einen Beobachter in Bewegung verkürzt sich der Raum selbst + ruhender Zwilling.
Ich habe schon versucht mit einer Zeichnung "scheinbare" und "tatsächliche" auseinander zu halten.
Wegen unterschiedlichen Wege durch die Raumzeit muss ich mir erst Gedanken machen.
Ich kann mich nur wiederholen - für den Beobachter in Bewegung müssen ruhende Myonen schneller zerfallen- diese Erwartung liefert die Mathematik.
Klar, so lange ich mich von ruhenden Myonen entferne ist deren Zerfallsrate gering, nähere ich mich aber diesen ruhenden Myonen steigt die Zerfallsrate entsprechend!
Relativität der Bewegung hat man künstlich erzeugt. Wenn es in unserem Universum nur zwei Objekte geben würde, dann ist die Bewegung tatsächlich relativ zu sehen, wenn aber Milliarden von Objekten existieren, dann ist die Entscheidung( was bewegt sich ich als Beobachter oder der anderer?) leicht zu treffen. Wir vergeben sogar Alterseingaben unserem Universum, da wir dieses als Raum (obwohl in diesem so viele Objekte mit unterschiedlichen Geschwindigkeiten rumfliegen) erkennen. Ich hoffe ich habe mich klar genug ausgedruckt.
Deswegen nochmal. Die Aussage
"In S' hat Myon-S eine größere Lebensdauer als Myon-S'."
http://de.wikipedia.org/wiki/Zeitdilatation_bewegter_Teilchen
kann nur bedingt richtig sein.
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
|
Registrieren
Login
FAQ
Suchen
