| Autor |
Nachricht |
Kyrous
Gast
|
 Kyrous Verfasst am: 15. Mai 2011 18:18 Titel: Zeit zum Leeren eines grossen, zylindrischen Wasserbehälters Kyrous Verfasst am: 15. Mai 2011 18:18 Titel: Zeit zum Leeren eines grossen, zylindrischen Wasserbehälters |
 |
|
Ich habe einen Stausee, der einfachheitshalber zylindrisch ist.
Es gibt eine Quelle die den Stausee füllt, und 2 regelbare Ventile die das Wasser zu den Generatoren rauslassen.
Die Ventile sind zuunterst am Staudamm angebracht...
Wie kann ich nun berechnen, wie lange es brauchen würde bis der Stausee leer bzw. voll ist.
Das Problem dabei ist, dass sich der Wasserdruck sich ja mit der Zeit immer ändert... 
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 16. Mai 2011 19:01 Titel: lampe16 Verfasst am: 16. Mai 2011 19:01 Titel: |
 |
|
Folgendes einfache Modell könnte genügen:
Für den Druck 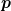 am Ausfluss unten und die Ausflussrate am Ausfluss unten und die Ausflussrate  gilt gilt
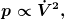
außerdem
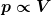
wegen der Abhängigkeit vom Pegel im Stausee.
Damit gilt
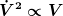
oder
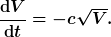
Diese Differentialgleichung kannst du lösen. Vorher musst du noch die Proportianalitäten durch die einschlägigen Gleichungen ersetzen.
Gruß, Lampe16
|
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 16. Mai 2011 21:27 Titel: Kyrous Verfasst am: 16. Mai 2011 21:27 Titel: |
 |
|
Sorry... Könntest du das noch für Leute erklären, denen bei dem Zeichen 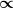 nur ein kleiner Fisch in den Sinn kommt... nur ein kleiner Fisch in den Sinn kommt... 
Ich hab gestern noch mit der Torricelli-Formel gearbeitet und die momentane Ausflussgeschwindigkeit (und -volumen) scheint damit berechenbar zu sein...
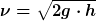
Weiss jemand hier weiter?
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 16. Mai 2011 21:46 Titel: lampe16 Verfasst am: 16. Mai 2011 21:46 Titel: |
 |
|
Der kleine Fisch heißt proportional oder verhältnisgleich.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 16. Mai 2011 23:45 Titel: lampe16 Verfasst am: 16. Mai 2011 23:45 Titel: |
 |
|
| Kyrous hat Folgendes geschrieben: | ... und die momentane Ausflussgeschwindigkeit (und -volumen) scheint damit berechenbar zu sein...
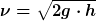
Weiss jemand hier weiter? |
Es kann so weitergehen:
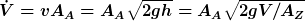
Damit hast du fast die Dgl., die ich oben skizziert habe. Es fehlt nur das Minuszeichen vor der Wurzel: Das Wasservolumen nimmt mit der Zeit ab.
 ist die Zylinder-Grundfläche und ist die Zylinder-Grundfläche und 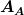 der Austrittsquerschnitt. der Austrittsquerschnitt.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 18. Mai 2011 18:16 Titel: lampe16 Verfasst am: 18. Mai 2011 18:16 Titel: |
 |
|
Nachdem der Fragesteller sich für seine Frage nicht mehr interessiert, ist vielleicht für jemand anders das Endergebnis noch interessant.
Die Auslaufzeit folgt aus der Lösung der Dgl. zu

_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 21. Mai 2011 01:09 Titel: Kyrous Verfasst am: 21. Mai 2011 01:09 Titel: |
 |
|
Hi,
Vielen Dank schonmal  Sieht gut aus.... Sieht gut aus....
Bei der letzten Gleichung (die für die Zeit), ist da nach dem Mal am Schluss was weggeschnitten worden? 
Und könntest du mir vllt. noch sagen wie sich die ändern würde, wenn zusätzlich zum Ausfluss noch ein konstanter Zufluss vorhanden wäre?
Danke schonmal im Vorraus.
|
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 21. Mai 2011 01:12 Titel: Kyrous Verfasst am: 21. Mai 2011 01:12 Titel: |
 |
|
|
... Oder auch wenn mehrere Ausflüsse vorhanden sind. Könnte man da für die Berechnung einfach alle Austrittsquerschnitte addieren?
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 21. Mai 2011 10:15 Titel: lampe16 Verfasst am: 21. Mai 2011 10:15 Titel: |
 |
|
| Kyrous hat Folgendes geschrieben: |
Bei der letzten Gleichung (die für die Zeit), ist da nach dem Mal am Schluss was weggeschnitten worden?
|
Nein, der Punkt ist das Satzzeichen am Ende des Satzes.
| Kyrous hat Folgendes geschrieben: |
Und könntest du mir vllt. noch sagen wie sich die ändern würde, wenn zusätzlich zum Ausfluss noch ein konstanter Zufluss vorhanden wäre?
|
Die Differentialgleichung dazu sieht einfach aus, ist aber nur noch numerisch zu lösen.
Wenn du Zahlenwerte hast, kann ich dir ein Beispiel rechnen. Oder du arbeitest dich in eine Mathematiksoftware wie Scilab (Freeware) ein. Damit geht das.
| Kyrous hat Folgendes geschrieben: |
... Oder auch wenn mehrere Ausflüsse vorhanden sind. Könnte man da für die Berechnung einfach alle Austrittsquerschnitte addieren?
|
Ja.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 21. Mai 2011 13:22 Titel: Kyrous Verfasst am: 21. Mai 2011 13:22 Titel: |
 |
|
Hi,
Im Nachhinein betrachtet, verstehe ich nicht was du damit meinst: "Die Auslaufzeit folgt aus der Lösung der Dgl. zu" ...
Was muss ich noch mit der Gleichung anstellen um das Resultat zu erhalten? 
Wir sind in der Schule in Mathe noch nicht soweit.
|
|
 |
fuss

Anmeldungsdatum: 25.05.2010
Beiträge: 519
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 21. Mai 2011 17:36 Titel: lampe16 Verfasst am: 21. Mai 2011 17:36 Titel: |
 |
|
| fuss hat Folgendes geschrieben: | | lampe16, welche DGL meinst du, die nur noch numerisch zu lösen ist? Wenn es um ein Problem wie dieses geht |
@fuss
Es geht um die Dgl
 . .
 und und 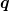 sind positive Konstanten. sind positive Konstanten.
Die Dgl. sieht einfacher zu lösen aus, als sie ist. Nach Trennung der Variablen stoße ich auf ein Integral, an dem ich scheitere. Mit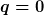 ist es natürlich harmlos. ist es natürlich harmlos.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 21. Mai 2011 17:50 Titel: lampe16 Verfasst am: 21. Mai 2011 17:50 Titel: |
 |
|
| Kyrous hat Folgendes geschrieben: | Hi,
Im Nachhinein betrachtet, verstehe ich nicht was du damit meinst: "Die Auslaufzeit folgt aus der Lösung der Dgl. zu" ...
Was muss ich noch mit der Gleichung anstellen um das Resultat zu erhalten? ?( |
Die Dgl. lösen. Ihre Lösung als Anfangswertproblem sei ) . Die habe ich nach der Zeit . Die habe ich nach der Zeit 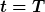 aufgelöst, zu der aufgelöst, zu der 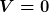 gilt. gilt.
| Kyrous hat Folgendes geschrieben: |
Wir sind in der Schule in Mathe noch nicht soweit.
|
Das kann ich gut verstehen, aber dann werden hier weitere Erklärungen zu Differentialgleichungen auch aufwendig. Das ist eher Hochschulmathematik.
Solange nichts zufließt, geht es relativ einfach (s.o.). Wenn aber Zufluss dabei ist, kann ich dir nur die Dgl. anbieten und eine numerische Lösung (Graph von ) ), wenn du mir entsprechende Zahlenwerte nennst (einschließlich Anfangsvolumen ), wenn du mir entsprechende Zahlenwerte nennst (einschließlich Anfangsvolumen 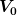 im Zylinder). im Zylinder).
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 21. Mai 2011 18:24 Titel: Keplerfan Verfasst am: 21. Mai 2011 18:24 Titel: |
 |
|
|
Ich sehe gerade, lösen kann man die Gleichung dann wohl immer noch nicht. Schade.
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 21. Mai 2011 19:12 Titel: lampe16 Verfasst am: 21. Mai 2011 19:12 Titel: |
 |
|
| Keplerfan hat Folgendes geschrieben: | | Ich sehe gerade, lösen kann man die Gleichung dann wohl immer noch nicht. Schade. |
Dein Vorschlag hilft möglicherweise trotzdem weiter. Ich brauche ja nicht unbedingt x(t). t(x) genügt auch. Ich bleibe dran.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 21. Mai 2011 19:39 Titel: Kyrous Verfasst am: 21. Mai 2011 19:39 Titel: |
 |
|
Was heisst denn "Dlg. lösen"? Ich weiss ja nicht einmal was sowas ist. Wie soll ich denn so etwas lösen??
Ich hab einfach mal die Werte eingesetzt und erstaunlicherweise stimmt das Resultat mit meiner simulierten Zeit überein...
Hab son Zylinder mal mit Java programmiert, und dann einfach mal die Ausflüsse, und wie sich dadurch das Volumen ändert, simuliert.
Aber die Simulation muss ich jetzt eben ausbauen, damit ich von schon von Anfang an weiss, wie lange es geht bis der Behälter leer ist.
Dazu bräuchte ich einfach eine Formel, wie genau die mathematisch hergeleitet wird ist mir jetzt im Moment nicht so wichtig...
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 22. Mai 2011 00:58 Titel: lampe16 Verfasst am: 22. Mai 2011 00:58 Titel: |
 |
|
| Kyrous hat Folgendes geschrieben: |
Dazu bräuchte ich einfach eine Formel, wie genau die mathematisch hergeleitet wird ist mir jetzt im Moment nicht so wichtig... |
Da du dich für die Zusammenhänge mangels einschlägiger Vorkenntnisse nicht interessierst, wird es für mich einfacher.
Hier ist ein Formelplan für den Behälter mit Abfluss und Zufluss 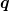 und dem Anfangsvolumen und dem Anfangsvolumen 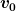 (übrige Bezeichnungen wie bisher): (übrige Bezeichnungen wie bisher):
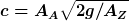

-\sqrt v+a\ln(\sqrt v_0-a)+\sqrt v_0))
In die letzte Formel kannst du  -Werte einsetzen und bekommst dann den Zeitpunkt -Werte einsetzen und bekommst dann den Zeitpunkt  , an dem das vorgegebene Volumen im Behälter ist. Je nach Zufluss kann der Behälter auch voller werden! Ein sich entleerender Behälter erreicht , an dem das vorgegebene Volumen im Behälter ist. Je nach Zufluss kann der Behälter auch voller werden! Ein sich entleerender Behälter erreicht 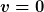 erst nach unendlich langer Zeit. Deshalb musst die für die Entleerungszeit ein kleines positives Restvolumen deiner Wahl vorgeben. erst nach unendlich langer Zeit. Deshalb musst die für die Entleerungszeit ein kleines positives Restvolumen deiner Wahl vorgeben.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 22. Mai 2011 09:45 Titel: Keplerfan Verfasst am: 22. Mai 2011 09:45 Titel: |
 |
|
| lampe16 hat Folgendes geschrieben: |
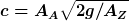

-\sqrt v+a\ln(\sqrt v_0-a)+\sqrt v_0))
|
Vielleicht etwas übersichtlicher:
+\sqrt v_0-\sqrt v))
PS: Bedeutet dies nicht, dass auch bei  endliche Abflusszeiten existieren, nämlich dann, wenn endliche Abflusszeiten existieren, nämlich dann, wenn 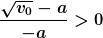 ? Die Abflusszeit sollte dann sein: ? Die Abflusszeit sollte dann sein:
+\sqrt v_0)=\frac{2}{c}(a\ln(\frac{a-\sqrt v_0}{a})+\sqrt v_0))
Nach dieser Zeit wäre der Behälter vollständig leer.
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 22. Mai 2011 10:54 Titel: franz Verfasst am: 22. Mai 2011 10:54 Titel: |
 |
|
Darf ich, aus Schönheitsgründen, skalierbare Klammern einsetzen 
)
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 22. Mai 2011 12:33 Titel: lampe16 Verfasst am: 22. Mai 2011 12:33 Titel: |
 |
|
@franz und keplerfan
Eure Umformungen gefallen mir.
Die Entleerungszeit bleibt aber 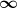 . Nehmt den einfachsten Fall q=0 (kein Zufluss). Dann gilt a=0 und eure Gl. beweist es. . Nehmt den einfachsten Fall q=0 (kein Zufluss). Dann gilt a=0 und eure Gl. beweist es.
Für q>0 gilt dasselbe. Die zu Grunde liegende Dgl. ist (zur Erinnerung) 
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 22. Mai 2011 12:46 Titel: Keplerfan Verfasst am: 22. Mai 2011 12:46 Titel: |
 |
|
Müsste sich aber für diesen Fall nicht die Auslaufzeit ergeben, die du bereits in einem früheren Posting ausgerechnet hattest?  )
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 22. Mai 2011 14:01 Titel: lampe16 Verfasst am: 22. Mai 2011 14:01 Titel: |
 |
|
| Keplerfan hat Folgendes geschrieben: | Müsste sich aber für diesen Fall nicht die Auslaufzeit ergeben, die du bereits in einem früheren Posting ausgerechnet hattest?  ) |
Ja, gut aufgepasst! Da ist noch etwas faul. Ich hoffe, ich komme bald dazu. Kannst ja gern schon mal mitdenken.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 22. Mai 2011 14:51 Titel: Keplerfan Verfasst am: 22. Mai 2011 14:51 Titel: |
 |
|
Ich vermute, dass Mathematica faulerweise die Betragsstriche im Logarithmus weggelassen hat. Es gilt ja:
 )
Ebenso sollte deshalb gelten
-2\sqrt{x} )
Die Formeln bleiben also wahrscheinlich alle gültig, aber das Argument des Logarithmus muss in Betragsstriche gepackt werden. Werd es bei Gelegenheit nochmal genau nachrechnen.
Mit dieser Korrektur würde sich für die Auslaufzeit momentan das ergeben (ich zitiere bzw. korrigiere die schöne Formel von franz):
)
Somit würde man für 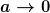 tatsächlich den bereits berechneten Wert erhalten, da der Logarithmus in dem Bereich, in dem der Limes gebildet wird, jetzt wieder definiert ist. tatsächlich den bereits berechneten Wert erhalten, da der Logarithmus in dem Bereich, in dem der Limes gebildet wird, jetzt wieder definiert ist.
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 22. Mai 2011 15:42 Titel: Keplerfan Verfasst am: 22. Mai 2011 15:42 Titel: |
 |
|
Seltsam ist nur: Der Behälter läuft nun immer leer, egal wie groß der Zufluss ist ...?
PS: Tut er nicht, die Auslaufzeit kann negativ werden. Ist ja auch logisch, in der Vergangenheit gibt es dem Modell nach ja einen Punkt, in dem noch kein Wasser zugeflossen war. Eine negative Auslaufzeit sagt also aus, dass der Behälter sich in der Zukunft niemals leeren wird.
Kann jemand die Formel numerisch bestätigen?
|
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 22. Mai 2011 20:38 Titel: Kyrous Verfasst am: 22. Mai 2011 20:38 Titel: |
 |
|
Hi,
Danke für eure zahlreichen Post,... aber ich check hier garnix mehr.
Was genau sollen diese Variablen sein?
"Hier ist ein Formelplan für den Behälter mit Abfluss und Zufluss q"
Abfluss und Zufluss sind doch 2 verschiedene Sachen, wie können die bitteschön die gleiche Variable benutzen?
Und was für eine Masseinheit hätte q überhaupt?
Und bezüglich euren Gedanken zur unendlichen Entleerzeit...
Die ist meiner bescheidenen Meinung nach theoretisch auch unendlich.
Ein unendlichstel Liter Wasser bleibt da immer drinn, da der Druck und somit auch der Ausfluss immer kleiner werden.
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 22. Mai 2011 21:25 Titel: Keplerfan Verfasst am: 22. Mai 2011 21:25 Titel: |
 |
|
q ist der Zufluss. Die neuen Variablen kannst du aus den alten berechnen, wie von lampe16 angegeben:
| lampe16 hat Folgendes geschrieben: |
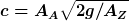

|
Ich bin eigentlich auch der Meinung, dass der Ausfluss unendlich lange dauern sollte, zumindest die Formel für die Ausflusszeit ohne Zufluss sagt aber etwas anderes. Mich würde interessieren, in wie fern du die erste berechnete Ausflusszeit (T) in deiner Simulation bestätigen konntest. (Hattest ja gesagt, das passt ganz gut.)
War am Ende noch Wasser im Behälter?
In der allgemeineren Formel für t oben schlägt sich eine "unendliche" Ausflusszeit meiner Meinung nach dadurch nieder, dass die Ausflusszeit vom Anfangszeitpunkt aus gemessen in der Vergangenheit liegt.
|
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 22. Mai 2011 22:07 Titel: Kyrous Verfasst am: 22. Mai 2011 22:07 Titel: |
 |
|
Also in meiner Simulation berechne ich die Werte jede halbe Sekunde neu.
Daher kommt es wahrscheinlich nicht in die Situation mit dem Unendlichstel Rest.
Das würd ja nur eintreten, wenn die Daten zu absolut jeder Zeit aktuell wären, sind sie aber in meiner Simulation ja nicht.
Also in der letzen halben Sekunde die Simuliert wird (kurz bevor der Behälter leer ist) ziehe ich einfach das ab, was zu genau dem Zeitpunkt rausgeflossen wäre, aber auf eine halbe Sekunde berechnet (linear). So wird der kleine Rest der nie rausfliessen würde, irgendwann durch die "ungenaue" Simulation einfach abgezogen...
Und was für eine Einheit hätte der Zufluss? Ich nehme mal an m³/s oder?
Was ich mich auch noch frage ist, was die neue Formel ergeben würde, wenn die Zuflüsse grösser sind als die Ausflüsse? Könnte man damit die Zeit berechnen, die es braucht um den Behälter zu füllen?
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 22. Mai 2011 22:24 Titel: lampe16 Verfasst am: 22. Mai 2011 22:24 Titel: |
 |
|
Ich fasse meinen Stand zusammen. Es gelten die vorher definierten Bezeichnungen, soweit hier nicht erklärt.
Das AWP
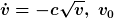
(Fall ohne Zufluss) hat die Lösung
.)
Der Endwert  wird nach der Zeit wird nach der Zeit
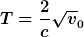
erreicht.
Das AWP
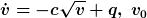
(Fall mit Zufluss) hat die Lösung
.)
Der Endwert  wird nach der Zeit wird nach der Zeit 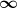 erreicht. erreicht.
Beide analytischen Lösungen erfüllen den Anfangswert und die jeweilige Dgl..
Die endliche/unendliche Zeit bis zum Beharrungswert im Fall ohne/mit Zufluss muss nicht irritieren. Nichtlineare Gln. sind immer für eine Überraschung gut
Mit dem folgenden Scilab-Code habe ich vollständige Übereinstimmung zwischen analytischer und numerischer Lösung gefunden, nicht nur für die angegebenen Inputs. Je nach den gewählten Eingabewerten stellt sich ein Endwert ein, der gleich null ist oder höher oder tiefer als der Anfangswert.
function v_=Dgl(t,v,c,q)
//v: Zeitfunktion des Zylinderinhalts/m^3
//c: Problemkonstante, s.u.
//q: Zufluss-Volumenstrom/(m^3/s)
v_=-c*real(sqrt(v))+q //Dgl. für Ausfluss-Modell nach Torricelli
//real wird nur für den Fall q=0 gebraucht.
endfunction
A_A=0.01; //A_A: Austrittsquerschnitt/m^2
A_Z=1; //A_Z: Zylinderquerschnitt/m^2
g=9.81; //g: Erdbeschleunigung/(m/s^2)
q=0.2; //Zufluss-Volumenstrom
v0=2; //Anfangsvolumen im Zylinder
c=A_A*sqrt(2*g/A_Z); //Problemkonstante
T=0:1:1000;
v=ode(v0,0,T,list(Dgl,c,q));//Dgl.-Solver
a=q/c; //Problemkonstante
v8=a^2// Beharrungswert des Volumens
ta=2/c*(a*log((sqrt(v0)-a)./(sqrt(v)-a))+sqrt(v0)-sqrt(v)); //analytische Lösung ta(v)
xdel();plot(T,v,'g',ta,v,'r--') //deckungsgleiche Kurven
ca=gca(); ca.box='off'; ca.x_location='origin'; ca.y_location='origin';
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 22. Mai 2011 22:29 Titel: lampe16 Verfasst am: 22. Mai 2011 22:29 Titel: |
 |
|
| Kyrous hat Folgendes geschrieben: |
Was ich mich auch noch frage ist, was die neue Formel ergeben würde, wenn die Zuflüsse grösser sind als die Ausflüsse? Könnte man damit die Zeit berechnen, die es braucht um den Behälter zu füllen? |
Ja, so ist es. Das Behältervolumen stellt sich mit der Zeit so ein, dass Abfluss und Zufluss sich kompensieren.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 23. Mai 2011 00:52 Titel: Kyrous Verfasst am: 23. Mai 2011 00:52 Titel: |
 |
|
| lampe16 hat Folgendes geschrieben: | | Kyrous hat Folgendes geschrieben: |
Was ich mich auch noch frage ist, was die neue Formel ergeben würde, wenn die Zuflüsse grösser sind als die Ausflüsse? Könnte man damit die Zeit berechnen, die es braucht um den Behälter zu füllen? |
Ja, so ist es. Das Behältervolumen stellt sich mit der Zeit so ein, dass Abfluss und Zufluss sich kompensieren. |
Aber wie kann ich denn die Füllzeit konkret berechnen? Die Ströme müssen sich ja nicht zwangsläufig kompensieren. Kann ja auch sein, dass der Behälter voll wird, bevor der Abfluss (durch die Druckzunahme) gleich gross wird, wie der (konstante) Zufluss...
|
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 01:21 Titel: Keplerfan Verfasst am: 23. Mai 2011 01:21 Titel: |
 |
|
| Keplerfan hat Folgendes geschrieben: |
 )
|
Du kannst diese Formel benutzen. Für v musst du dann das Volumen des Behälters einsetzen und für  das Anfangsvolumen der Flüssigkeit. das Anfangsvolumen der Flüssigkeit.
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 23. Mai 2011 10:24 Titel: lampe16 Verfasst am: 23. Mai 2011 10:24 Titel: |
 |
|
| Kyrous hat Folgendes geschrieben: | | Aber wie kann ich denn die Füllzeit konkret berechnen? Die Ströme müssen sich ja nicht zwangsläufig kompensieren. Kann ja auch sein, dass der Behälter voll wird, bevor der Abfluss (durch die Druckzunahme) gleich gross wird, wie der (konstante) Zufluss... |
Mit dem Scilab-Code (t(v)-Formel) habe ich ein Beispiel gerechnet. Es handelt sich um den Füllvorgang eines Wassereimers mit Loch im Boden.
Die Eingabedaten sind:
A_A=1e-4; //A_A: Austrittsquerschnitt/m^2
A_Z=400e-4; //A_Z: Zylinderquerschnitt/m^2
g=9.81; //g: Erdbeschleunigung/(m/s^2)
q=200e-6//0.2; //Zufluss-Volumenstrom
v0=0; //Anfangsvolumen im Zylinder
Was jetzt die Füllzeit ist, musst du definieren, z.B. Zeit nach Erreichen von 99 % des Endwerts.
| Beschreibung: |
|

Download |
| Dateiname: |
PhysikerBoardEimerMitLoch.jpg |
| Dateigröße: |
37.29 KB |
| Heruntergeladen: |
5030 mal |
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 23. Mai 2011 17:16 Titel: lampe16 Verfasst am: 23. Mai 2011 17:16 Titel: |
 |
|
@Kyrous
Ich beantworte jetzt auch, wie schon Keplerfan, deinen Ruf nach der "einfachen Formel" und berücksichtige deinen vorläufigen Wunsch nach Weglassen uninteressanter Herleitungen:
Für die Füllzeit oder die Entleerungszeit oder allgemein die Übergangszeit von einer Anfangsfüllmenge 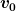 in eine sich nicht mehr ändernde Endfüllmenge in eine sich nicht mehr ändernde Endfüllmenge 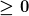
gilt die Formel
 )
mit
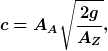
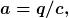
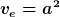 und und
,)
wobei 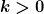 auf einen Wert nahe bei null, z.B. auf 0.01 oder 0.001 oder ... gesetzt werden soll. auf einen Wert nahe bei null, z.B. auf 0.01 oder 0.001 oder ... gesetzt werden soll.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 23. Mai 2011 17:26 Titel: Keplerfan Verfasst am: 23. Mai 2011 17:26 Titel: |
 |
|
Was sagst du denn zur Frage der Betragsstriche im Logarithmus-Teil der Stammfunktiion? Meiner Meinung nach müssen da, wie oben ausgeführt, Betragsstriche stehen, was den Definitionsbereich von 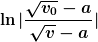 noch ein wenig erweitert. noch ein wenig erweitert.
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 23. Mai 2011 17:57 Titel: lampe16 Verfasst am: 23. Mai 2011 17:57 Titel: |
 |
|
Ich stelle mir eine Skala vor, auf der 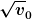 den Anfangswert und den Anfangswert und  den Endwert der Füllung abbildet. Die momentane Füllung bleibt während jedes Übergangsvorgangs in diesem Intervall, so dass ich keine Situation sehe, wo der Bruch mal negativ werden kann. den Endwert der Füllung abbildet. Die momentane Füllung bleibt während jedes Übergangsvorgangs in diesem Intervall, so dass ich keine Situation sehe, wo der Bruch mal negativ werden kann.
Hast du denn einen konkreten Fall im Blick, wo das auftritt und die Betragsstriche dann einen realen Vorgang richtig beschreiben helfen?
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Keplerfan

Anmeldungsdatum: 19.05.2011
Beiträge: 252
|
 Keplerfan Verfasst am: 24. Mai 2011 20:15 Titel: Keplerfan Verfasst am: 24. Mai 2011 20:15 Titel: |
 |
|
Ich war nur von der Rechnerei ausgegangen, dass a der Endwert ist, das hatte ich noch gar nicht kapiert.  Ich denke, deine Argumentation ist dann schlüssig. Ich denke, deine Argumentation ist dann schlüssig.
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 25. Mai 2011 13:26 Titel: lampe16 Verfasst am: 25. Mai 2011 13:26 Titel: |
 |
|
Doch noch eine Bemerkung zur Betragsfunktion: In meiner ersten Lösung ) mit der Differenz der mit der Differenz der 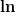 -Terme wären die Betragsstriche dringend nötig gewesen. Erst durch deine Zusammenfassung per Bruch konnten sie entfallen. -Terme wären die Betragsstriche dringend nötig gewesen. Erst durch deine Zusammenfassung per Bruch konnten sie entfallen.
Ich habe auch nochmal ins Mathebuch geschaut und
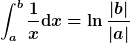
gefunden, wobei das Intervall [a,b] den Nullpunkt nicht enthalten darf.
Auch hier sind die Beträge wegen der Bedingung eigentlich überflüssig: Der Bruch wird immer positiv sein. Weil ich den Lehrbuchverfasser aber hoch respektiere, würde ich die Striche jetzt auch setzen. Damit sie nicht ganz arbeitlos sind, im Zähler und Nenner separat.
Betragsbildungen haben mir schon viel Ärger gemacht und sind öfter vermeidbar als man denkt. Ich hatte die Lösung ) mit Bruch und ohne Betragsfunktion in die umgeformte Dgl. mit Bruch und ohne Betragsfunktion in die umgeformte Dgl. 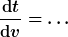 eingesetzt und festgestellt, dass sie erfüllt ist. Damit waren die Striche in der Bruchform der Lösung entbehrlich. eingesetzt und festgestellt, dass sie erfüllt ist. Damit waren die Striche in der Bruchform der Lösung entbehrlich.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
Kyrous
Gast
|
 Kyrous Verfasst am: 25. Mai 2011 15:52 Titel: Kyrous Verfasst am: 25. Mai 2011 15:52 Titel: |
 |
|
| lampe16 hat Folgendes geschrieben: | @Kyrous
Ich beantworte jetzt auch, wie schon Keplerfan, deinen Ruf nach der "einfachen Formel" und berücksichtige deinen vorläufigen Wunsch nach Weglassen uninteressanter Herleitungen:
Für die Füllzeit oder die Entleerungszeit oder allgemein die Übergangszeit von einer Anfangsfüllmenge 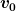 in eine sich nicht mehr ändernde Endfüllmenge in eine sich nicht mehr ändernde Endfüllmenge 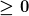
gilt die Formel
 )
mit
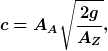
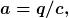
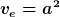 und und
,)
wobei 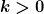 auf einen Wert nahe bei null, z.B. auf 0.01 oder 0.001 oder ... gesetzt werden soll. auf einen Wert nahe bei null, z.B. auf 0.01 oder 0.001 oder ... gesetzt werden soll. |
Was ist denn da jetzt k und wo in der Formel ist die Endfüllmenge????
Und könntest du vllt noch dazu schreiben, was die Variablen alle für Masseinheiten haben? 
|
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
 lampe16 Verfasst am: 25. Mai 2011 18:52 Titel: lampe16 Verfasst am: 25. Mai 2011 18:52 Titel: |
 |
|
| Kyrous hat Folgendes geschrieben: | | Was ist denn da jetzt k |
Lies die Zeile, in der 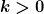 steht. steht.
| Kyrous hat Folgendes geschrieben: | | und wo in der Formel ist die Endfüllmenge???? |
Die Endfüllmenge 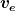 geht in die Formel durch geht in die Formel durch  ein. Die kannst du aber nicht vorgeben. Sie stellt sich als Ergebnis nach der Zeit ein. Die kannst du aber nicht vorgeben. Sie stellt sich als Ergebnis nach der Zeit  ein. ein.
Bitte mach dir klar, dass du zur Berechnung der Übergangszeit genau 5 Größen vorgeben musst: 
| Kyrous hat Folgendes geschrieben: | | Und könntest du vllt noch dazu schreiben, was die Variablen alle für Masseinheiten haben? |
S. o.!
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
 |
|


















 Sieht gut aus....
Sieht gut aus....
