| Autor |
Nachricht |
Timo U.
Gast
|
 Timo U. Verfasst am: 23. Aug 2013 17:00 Titel: Bedeutung Ableitung nach Winkel (schiefer Wurf) Timo U. Verfasst am: 23. Aug 2013 17:00 Titel: Bedeutung Ableitung nach Winkel (schiefer Wurf) |
 |
|
Meine Frage:
Hallo zusammen
ich hab heute aus Spaß einmal die Funktion einer Wurfparabel abgeleitet.
Die erste Ableitung nach x (Weg) entspricht ja der Steigung an einer bestimmten Stelle x bezogen auf den Untergrund.
Was aber ist die theoretische Bedeutung der Ableitung nach dem Abwurfswinkel alpha?
Viele Grüße Timo
Meine Ideen:
Ich hab ehrlich gesagt keine treffende Idee
Winkelgeschwindigkeit ergibt für mich keinen Sinn in dem Fall |
|
 |
Timo U.
Gast
|
 Timo U. Verfasst am: 23. Aug 2013 17:05 Titel: Timo U. Verfasst am: 23. Aug 2013 17:05 Titel: |
 |
|
|
könnte es sich um den minimalen und maximalen Abwurfwinkel handeln? |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 23. Aug 2013 18:43 Titel: Jayk Verfasst am: 23. Aug 2013 18:43 Titel: |
 |
|
Welchen mathematischen Kenntnisstand hast du denn?
Die geometrische Interpretation als Anstieg geht auf Leibniz zurück (Schreibweise  ). Newton hatte eine etwas andere Absicht: er sah die Ableitung als etwas Dynamisches, z.B. wie ändert sich die Geschwindigkeit mit der Zeit -> Beschleunigung (Schreibweise ). Newton hatte eine etwas andere Absicht: er sah die Ableitung als etwas Dynamisches, z.B. wie ändert sich die Geschwindigkeit mit der Zeit -> Beschleunigung (Schreibweise  ). Diese Sichtweise ist natürlich allgemeiner, z.B. Ableitung von irgendwas nach dem Winkel = wie verändert sich dieses etwas, wenn sich der Winkel ändert? Nimm mal an, du kennst den Wert einer Funktion ). Diese Sichtweise ist natürlich allgemeiner, z.B. Ableitung von irgendwas nach dem Winkel = wie verändert sich dieses etwas, wenn sich der Winkel ändert? Nimm mal an, du kennst den Wert einer Funktion ) an der Stelle an der Stelle 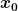 sowie die Ableitung an dieser Stelle sowie die Ableitung an dieser Stelle  = \left. \frac{\dd f(x)}{\dd x} \right\vert_{x=x_0}) und möchtest wissen, wie groß er an der Stelle und möchtest wissen, wie groß er an der Stelle  ist. Dann ist ist. Dann ist  \approx f(x_0) + a \cdot f'(x_0)) unter Umständen eine gute Näherung, so wie du unter Umständen eine gute Näherung, so wie du 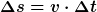 anwenden darfst, wenn sich die Geschwindigkeit nicht ändert. Der korrekte Zusammenhang umfasst noch weitere Ableitungen und heißt Taylorentwicklung (die Ableitung ändert ihren Wert, und die Ableitung der Ableitung ändert ihren Wert, ...): anwenden darfst, wenn sich die Geschwindigkeit nicht ändert. Der korrekte Zusammenhang umfasst noch weitere Ableitungen und heißt Taylorentwicklung (die Ableitung ändert ihren Wert, und die Ableitung der Ableitung ändert ihren Wert, ...):  = f(x_0) + f'(x_0) \cdot a + \frac{f''(x_0)}{2} \cdot a^2 + \frac{f'''(x_0)}{6} \cdot a^3 + \dots)
Ich weiß nicht, was genau du abgeleitet hast. Wenn du zum Beispiel einen funktionalen Zusammenhang zwischen der Wurfweite ) und dem Abwurfwinkel und dem Abwurfwinkel  kennst, kannst du über die Ableitung berechnen, für welchen Abwurfwinkel die Wurfweite stationär ist (d.h. lokales Minimum, lokales Maximum oder Sattelpunkt - was der Fall ist, bekommst du über die zweite, bzw. falls diese null ist, alle weiteren Ableitungen heraus). Dafür bildest du die Ableitung kennst, kannst du über die Ableitung berechnen, für welchen Abwurfwinkel die Wurfweite stationär ist (d.h. lokales Minimum, lokales Maximum oder Sattelpunkt - was der Fall ist, bekommst du über die zweite, bzw. falls diese null ist, alle weiteren Ableitungen heraus). Dafür bildest du die Ableitung ) und forderst, dass diese null wird, weil sich die Weite mit einer kleinen Veränderung des Winkels (in erster Ordnung, sozusagen) nicht ändern darf: bei einem Maximum ist sie bei leicht kleineren Winkeln kleiner, bei leicht größeren auch, also muss der Anstieg direkt am Maximum null sein. Umstellen nach und forderst, dass diese null wird, weil sich die Weite mit einer kleinen Veränderung des Winkels (in erster Ordnung, sozusagen) nicht ändern darf: bei einem Maximum ist sie bei leicht kleineren Winkeln kleiner, bei leicht größeren auch, also muss der Anstieg direkt am Maximum null sein. Umstellen nach  ergibt dann z.B. den idealen Abwurfwinkel (dieser beträgt, wenn die Abwurfhöhe gleich die Zielhöhe ist, 45°, wenn man den Luftwiderstand vernachlässigt). Kannst du ja mal ausprobieren... ergibt dann z.B. den idealen Abwurfwinkel (dieser beträgt, wenn die Abwurfhöhe gleich die Zielhöhe ist, 45°, wenn man den Luftwiderstand vernachlässigt). Kannst du ja mal ausprobieren... |
|
 |
klaus.leiter
Anmeldungsdatum: 26.08.2013
Beiträge: 1
|
 klaus.leiter Verfasst am: 26. Aug 2013 10:26 Titel: klaus.leiter Verfasst am: 26. Aug 2013 10:26 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: | Welchen mathematischen Kenntnisstand hast du denn?
Die geometrische Interpretation als Anstieg geht auf Leibniz zurück (Schreibweise  ). Newton hatte eine etwas andere Absicht: er sah die Ableitung als etwas Dynamisches, z.B. wie ändert sich die Geschwindigkeit mit der Zeit -> Beschleunigung (Schreibweise ). Newton hatte eine etwas andere Absicht: er sah die Ableitung als etwas Dynamisches, z.B. wie ändert sich die Geschwindigkeit mit der Zeit -> Beschleunigung (Schreibweise  ). Diese Sichtweise ist natürlich allgemeiner, z.B. Ableitung von irgendwas nach dem Winkel = wie verändert sich dieses etwas, wenn sich der Winkel ändert? Nimm mal an, du kennst den Wert einer Funktion ). Diese Sichtweise ist natürlich allgemeiner, z.B. Ableitung von irgendwas nach dem Winkel = wie verändert sich dieses etwas, wenn sich der Winkel ändert? Nimm mal an, du kennst den Wert einer Funktion ) an der Stelle an der Stelle 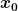 sowie die Ableitung an dieser Stelle sowie die Ableitung an dieser Stelle  = \left. \frac{\dd f(x)}{\dd x} \right\vert_{x=x_0}) und möchtest wissen, wie groß er an der Stelle und möchtest wissen, wie groß er an der Stelle  ist. Dann ist ist. Dann ist  \approx f(x_0) + a \cdot f'(x_0)) unter Umständen eine gute Näherung, so wie du unter Umständen eine gute Näherung, so wie du 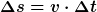 anwenden darfst, wenn sich die Geschwindigkeit nicht ändert. Der korrekte Zusammenhang umfasst noch weitere Ableitungen und heißt Taylorentwicklung (die Ableitung ändert ihren Wert, und die Ableitung der Ableitung ändert ihren Wert, ...): anwenden darfst, wenn sich die Geschwindigkeit nicht ändert. Der korrekte Zusammenhang umfasst noch weitere Ableitungen und heißt Taylorentwicklung (die Ableitung ändert ihren Wert, und die Ableitung der Ableitung ändert ihren Wert, ...):  = f(x_0) + f'(x_0) \cdot a + \frac{f''(x_0)}{2} \cdot a^2 + \frac{f'''(x_0)}{6} \cdot a^3 + \dots)
Ich weiß nicht, was genau du abgeleitet hast. Wenn du zum Beispiel einen funktionalen Zusammenhang zwischen der Wurfweite ) und dem Abwurfwinkel und dem Abwurfwinkel  kennst, kannst du über die Ableitung berechnen, für welchen Abwurfwinkel die Wurfweite stationär ist (d.h. lokales Minimum, lokales Maximum oder Sattelpunkt - was der Fall ist, bekommst du über die zweite, bzw. falls diese null ist, alle weiteren Ableitungen heraus). Dafür bildest du die Ableitung kennst, kannst du über die Ableitung berechnen, für welchen Abwurfwinkel die Wurfweite stationär ist (d.h. lokales Minimum, lokales Maximum oder Sattelpunkt - was der Fall ist, bekommst du über die zweite, bzw. falls diese null ist, alle weiteren Ableitungen heraus). Dafür bildest du die Ableitung ) und forderst, dass diese null wird, weil sich die Weite mit einer kleinen Veränderung des Winkels (in erster Ordnung, sozusagen) nicht ändern darf ( http://winkelberechnung.com/ ): bei einem Maximum ist sie bei leicht kleineren Winkeln kleiner, bei leicht größeren auch, also muss der Anstieg direkt am Maximum null sein. Umstellen nach und forderst, dass diese null wird, weil sich die Weite mit einer kleinen Veränderung des Winkels (in erster Ordnung, sozusagen) nicht ändern darf ( http://winkelberechnung.com/ ): bei einem Maximum ist sie bei leicht kleineren Winkeln kleiner, bei leicht größeren auch, also muss der Anstieg direkt am Maximum null sein. Umstellen nach  ergibt dann z.B. den idealen Abwurfwinkel (dieser beträgt, wenn die Abwurfhöhe gleich die Zielhöhe ist, 45°, wenn man den Luftwiderstand vernachlässigt). Kannst du ja mal ausprobieren... ergibt dann z.B. den idealen Abwurfwinkel (dieser beträgt, wenn die Abwurfhöhe gleich die Zielhöhe ist, 45°, wenn man den Luftwiderstand vernachlässigt). Kannst du ja mal ausprobieren... |
Sehr gut erklärt. Ich hab das mit deinem (Jayk) Ansatz auch mal probiert und siehe da, es hat geklappt. Vielen Dank für die ausführliche Erklärung.
Hat mir wirklich weitergeholfen.  |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18068
|
 TomS Verfasst am: 26. Aug 2013 10:38 Titel: TomS Verfasst am: 26. Aug 2013 10:38 Titel: |
 |
|
Zunächst haben wir die Wurfparabel als Funktion der Zeit sowie mit einem (von mehreren) Parametern alpha
, y_\alpha(t)))
Daraus bestimmen wir
)
und damit
))
Nun zur Frage
| Timo U. hat Folgendes geschrieben: | | Was aber ist die theoretische Bedeutung der Ableitung nach dem Abwurfwinkel? |
Was genau, d.h. welche Funktion bzw. o.g. Darstellung der Wurfparabel hast du nach alpha abgeleitet?
Zur Bedeutung des Abwurfwinkels:
1) Für die Abwurfgeschwindigkeit kannst du schreiben
 = \left(\frac{d\vec{r}_\alpha(t)}{dt}\right)_{t=0} = v(t=0)\,\cdot\,(\cos\alpha,\sin\alpha))
D.h. alpha beschreibt die Steigung der Wurfparabel im Abwurfpunkt.
2) Für eine Ableitung fällt mir folgende Anwendung ein: du bestimmst die beiden Nullstellen der Wurfparabel als Funktion y(x); daraus folgen zwei Lösungen für x mit Parameter alpha, d.h.
 = 0\;\to\; x_{1,2}(\alpha))
Die erste Nullstelle ist trivialerweise x=0, die zweite entspricht der Wurfweite.
Nun berechnest du
}{d\alpha} = 0)
und bestimmst damit den optimalen Abwurfwinkel für maximale Weite.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
territrades
Gast
|
 territrades Verfasst am: 12. Sep 2013 20:14 Titel: territrades Verfasst am: 12. Sep 2013 20:14 Titel: |
 |
|
Die Frage ist interessant, und wie immer versuch einige solchen Fragen mit dem mathematischen Hammer zu erschlagen. Also:
Du hast also die Wurfparabel y(x). Wenn du die nach x ableitest, erhälst du an jeder Stelle die Steigung der Kurve.
Der Winkel kommst ebenso wie die Abwurfgeschwindigkeit in der Formel als Parameter vor, man könnte also ) schreiben. Wenn du jetzt nach schreiben. Wenn du jetzt nach  ableiten willst, musst du das ganze eher als Funktion von zwei Variablen aufgreifen: ableiten willst, musst du das ganze eher als Funktion von zwei Variablen aufgreifen:
)
Der Funktionsgraph ist jetzt keine "Linie" mehr, sondern eine Fläche, das ganze sieht dann aus wie ein "Gebirge".
Jetzt hat man zwei Variablen, und kann verschiedene Ableitungen bilden. Die "richtige" Ableitung leitet nach beiden Variablen ab und ist ein Vektor, der Vektor der an jedem Punkt in die Richtung des größten Anstiegs zeigt. Du willst aber nur nach einer Variablen ableiten, das nennt man partielle Ableitung und schreibt:  . Was bedeutet das nun? Das Ergebnis hängt immer noch von x und . Was bedeutet das nun? Das Ergebnis hängt immer noch von x und  ab, und gibt an wie stark sich der y-Wert (also die Höhe) bei gegebenen x und ab, und gibt an wie stark sich der y-Wert (also die Höhe) bei gegebenen x und  ändert, wenn der Winkel variiert wird. Der Wert dieser Ableitungen wird betragsmäßig sicherlich immer größer für größere x, da kleine Änderung am Abwurfwinkel größere Auswirkungen haben, je weiter das Objekt gewurfen wird. ändert, wenn der Winkel variiert wird. Der Wert dieser Ableitungen wird betragsmäßig sicherlich immer größer für größere x, da kleine Änderung am Abwurfwinkel größere Auswirkungen haben, je weiter das Objekt gewurfen wird.
PS: Ich habe das mal so für 12.-Klässler geschrieben, weil ich mir ziemlich genau die selbe Frage in langweiligen Englischstunden in der 12. Klasse gestellt habe. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 12. Sep 2013 20:26 Titel: Jayk Verfasst am: 12. Sep 2013 20:26 Titel: |
 |
|
Damit ist nur leider überhaupt nichts gesagt. Dass du auf partielle Ableitungen eingehst, ist nicht wirklich nötig. Du kannst genauso gut x als konstant auffassen (nichts anderes ist ja die partielle Ableitung) und stehst dann vor dem Problem: Was bedeutet ) ? Du erklärst das mit dem Anstieg der Tangente an den Graphen. Entweder du stellst dich auf den Standpunkt, dass das die Bedeutung ist. Dann wäre die Frage aber bereits mit dem Post des Fragestellers geklärt gewesen, denn das weiß er ja. Es geht ja gerade darum, was die Ableitung nach einem Winkel bedeutet. Wenn du aber in deiner Erklärung die Natur des Winkels untergräbst, ist das ziemlich sinnlos. Tatsächlich hat die Ableitung eines Winkels keine anschauliche Bedeutung, außer "wie ändert sich f in erster Ordnung bei einer Änderung des Winkels". ? Du erklärst das mit dem Anstieg der Tangente an den Graphen. Entweder du stellst dich auf den Standpunkt, dass das die Bedeutung ist. Dann wäre die Frage aber bereits mit dem Post des Fragestellers geklärt gewesen, denn das weiß er ja. Es geht ja gerade darum, was die Ableitung nach einem Winkel bedeutet. Wenn du aber in deiner Erklärung die Natur des Winkels untergräbst, ist das ziemlich sinnlos. Tatsächlich hat die Ableitung eines Winkels keine anschauliche Bedeutung, außer "wie ändert sich f in erster Ordnung bei einer Änderung des Winkels". |
|
 |
|
|
















