| Autor |
Nachricht |
neuerstudent
Gast
|
 neuerstudent Verfasst am: 28. Aug 2013 00:05 Titel: totale vs partielle |
 |
|
es geht allg um zwangsbedigungen
sei f(x,t)=x+y+z=0
df/dt=x'+y'+z'=0
aber wenn ich partiell nach x, y oder z ableite
dann gilt
df/dx=1 wieso ist hier eins und nicht null |
|
 |
yellowfur
Moderator
Anmeldungsdatum: 30.11.2008
Beiträge: 804
|
| yellowfur Verfasst am: 28. Aug 2013 00:40 Titel: |
|
|
Du hast ,y(t),z(t),t)=x+y+z) . x,y und z sind so beschaffen, dass +y(t)+z(t)=0) .
Bei der totalen Ableitung gilt das auch:
Wenn du aber partiell nach x ableitest, dann verschwinden die Terme 
und übrig bleibt
 ,
denn Null kommt nur heraus, wenn die Terme y und z noch daraufaddiert werden, welche hier aber schon null sind.
_________________
Wenn du einen Traum hast, dann folge ihm. Wer weiß, wo er dich hinführen könnte. |
|
|
neuerstudent
Gast
|
| neuerstudent Verfasst am: 28. Aug 2013 01:23 Titel: |
|
|
ich könnte ja f durch 0 ersetzen
also df/dx=d0/dx=0?
warum darf man das nich
wenn die Terme y und z noch daraufaddiert werden
wie meinst du
kannst du mir zeigen wieso das gilt |
|
|
12345
Gast
|
| 12345 Verfasst am: 28. Aug 2013 08:57 Titel: |
|
|
Weil du damit implizierst, dass 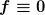 ist, also das f für ALLE  gleich null ist. In Wirklichkeit ist deine Null hier aber eine Funktion die explizit von abhängt, d.h. ) ! |
|
|
neuerstudent
Gast
|
| neuerstudent Verfasst am: 28. Aug 2013 11:46 Titel: |
|
|
| yellowfur hat Folgendes geschrieben: | Du hast . x,y und z sind so beschaffen, dass .
Bei der totalen Ableitung gilt das auch:
|
@12345 soweit verstanden
aber wieso folgt für die totale ableitung df/dt=0
bzw. x'+y'+z'=0 aus was folgt das |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 28. Aug 2013 12:06 Titel: |
|
|
| neuerstudent hat Folgendes geschrieben: |
@12345 soweit verstanden
aber wieso folgt für die totale ableitung df/dt=0
bzw. x'+y'+z'=0 aus was folgt das |
Das folgt daraus, dass die Zwangsbedingung f = 0 für alle Zeiten t gilt. Darum ist dann auch die Ableitung nach t gleich 0.
(Wie schon gesagt wurde: Im Gegensatz zu den Ableitungen nach x, y oder z.. da f=0 eben nicht für alle x,y,z gilt.) |
|
|
yellowfur
Moderator
Anmeldungsdatum: 30.11.2008
Beiträge: 804
|
| yellowfur Verfasst am: 28. Aug 2013 12:35 Titel: |
|
|
Genau. Dem ist nichts mehr hinzuzufügen. Danke.
_________________
Wenn du einen Traum hast, dann folge ihm. Wer weiß, wo er dich hinführen könnte. |
|
|
neuerstudent
Gast
|
| neuerstudent Verfasst am: 28. Aug 2013 13:32 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | .... da f=0 eben nicht für alle x,y,z gilt.) |
es muss doch für alle x,y,z f=0 gelten?
oder lautetim allgmeinen f=x+y+z
und nur für einige x,y,z gilt
f=0 |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 28. Aug 2013 13:37 Titel: |
|
|
| neuerstudent hat Folgendes geschrieben: |
oder lautetim allgmeinen f=x+y+z
und nur für einige x,y,z gilt
f=0 |
Ja, so ist es richtig: f(x,y,z)=x+y+z.
Und das definiert Dir bestimmte Werte von (x,y,z) für die f=0 gilt, z.B. (x,y,z)=(0,-1,1). |
|
|
neuerstudent
Gast
|
| neuerstudent Verfasst am: 28. Aug 2013 14:15 Titel: |
|
|
gäbe es hier ein unterschied zwischer totaler und partieller zeitableitung
was genau würde es ändern? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 28. Aug 2013 14:24 Titel: |
|
|
Die totale Zeitableitung von f ist (wegen der Kettenregel)
und wegen f=0 für alle t ist das alles auch gleich 0.
Die partielle Ableitung ist die Ableitung von f nach dem expliziten Argument t, also in diesem fall
Dies ist unabhängig von allem anderen schon 0, weil f nicht von t abhängt.
PS: Die partielle Ableitung von f nach x ist z.B.  .
PPS: Gerade Physiker sind oft nicht besonders vorsichtig, ob sie totale oder partielle Ableitungen schreiben, weil sowieso klar ist was gemeint ist. |
|
|
neuerstudent
Gast
|
| neuerstudent Verfasst am: 28. Aug 2013 15:34 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | Die totale Zeitableitung von f ist (wegen der Kettenregel)
und wegen f=0 für alle t ist das alles auch gleich 0.
|
haste nich gesagt dass es nur für einige x,y und z f=0 gilt oder übersehe ich wieder was
| jh8979 hat Folgendes geschrieben: | | neuerstudent hat Folgendes geschrieben: |
oder lautetim allgmeinen f=x+y+z
und nur für einige x,y,z gilt
f=0 |
Ja, so ist es richtig: f(x,y,z)=x+y+z.
Und das definiert Dir bestimmte Werte von (x,y,z) für die f=0 gilt, z.B. (x,y,z)=(0,-1,1). |
 |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 28. Aug 2013 15:42 Titel: |
|
|
| neuerstudent hat Folgendes geschrieben: |
haste nich gesagt dass es nur für einige x,y und z f=0 gilt oder übersehe ich wieder was
|
ja und die die f=0 erfuellen, erfuellen auch df/dt=0, wobei df/dt gegeben ist durch die Formel, die ich oben aufgeschrieben hab. |
|
|
neuerstudent
Gast
|
| neuerstudent Verfasst am: 01. Sep 2013 20:57 Titel: |
|
|
eine frage die gerade aufgetaucht ist:
bei partieller ableitung ist es wichtig zusagen was konstant gehalten
richitg?
also wenn ich
f=x+y+z=0
partiell nach t ableite
aber x,y und z sollen sich verändern
dann ist im diesen fall
die totale und partielle ableitung gleich? |
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 01. Sep 2013 21:45 Titel: |
|
|
Im Prinzip schon. Meiner Ansicht nach ist das aber ein algebraisches Problem, denn man muss sich irgendwie festlegen, welche Menge(n) auf welche abgebildet werden. Diesen Luxus kann man sich natürlich in der Physik nicht leisten, weil diese Entscheidung wohl vom konkreten Problem abhängt, aber wenn du dir in einem Analysis-Buch durchliest, wie die partielle Ableitung definiert ist, wirst du nicht finden, dass man angeben müsste, was konstant gehalten wird. Eine Funktion hängt von mehreren Argumenten ab. Wenn du partiell nach einem ableitest, werden alle anderen konstant gehalten:
 := \lim_{h \to 0} \frac{f(x_1, \dots, x_i + h, \dots, x_n) - f(x_1, \dots, x_i, \dots, x_n)}{h})
Allerdings setzt diese Definition voraus, dass die Argumente unabhängig voneinander sind. Wenn sich x, y und z miteinander oder mit t verändern, dann wird nicht mehr  \rbrace) abgebildet, sondern du hast eine Komposition (ich bin hier auf dem Standpunkt, eine Abbildung und ihren Graphen als identisch aufzufassen), wenn z.B. alle von t abhängen, wird in Wirklichkeit nur  abgebildet. Dann wären natürlich totale und partielle Ableitung gleich, weil es effektiv nur einen Parameter gibt. |
|
|
|
Registrieren
Login
FAQ
Suchen
