| Autor |
Nachricht |
Steve08
Anmeldungsdatum: 27.03.2008
Beiträge: 40
|
 Steve08 Verfasst am: 07. Mai 2008 17:58 Titel: Partielle Ableitung - Maximalfehler Steve08 Verfasst am: 07. Mai 2008 17:58 Titel: Partielle Ableitung - Maximalfehler |
 |
|
Hallo Physik-Boardler,
ich habe folgendes Problem, ich habe an der FH geräde ein Physik-Praktikum auszuarbeiten, dass sich mit Kraft und Kraftzerlegung beschäftigt, das heist eine Balkenwaage mit 2 Drehmomenten usw... Denke das ist nicht so wichtig.
Es geht dabei wie schon gesagt um die Berechnung des Maximalfehler einer Kraft F die sich nach folgender Formel berechnen lässt:
=\frac{b\cdot m\cdot g}{a\cdot \cos\alpha} )
Der Maximalfehler lässt sich wie folgt dabei berechnen:

Hoffe ihr wisst das immer nach den Strichen das delta groß sein soll...
[Latex-Tipp: Partielle Abeitungen gehen mit \partial, große Deltas mit \Delta , Mal-Punkte mit \cdot . Ich habs mal verschönert, Schönen Gruß, dermarkus]
Übrigens a= Abstand a vom Drehpukt der Waage bis zum 1. Drehmoment
b= Abstand b " 2. "
alpha = Winkel in dem die Kraft angreift
m = Masse des an der Waage hängenden Körper
g = Erdbeschleunigung
Nun mach ich die partielle Ableitung die wie folgt bei mir aussieht:
}{a\cdot (\cos\alpha)^{2}} \right| \cdot \Delta \alpha)
Wenn ich nun meine Werte einsetze also a=20cm, b=25cm, m=102,2g, alpha=45°, delta a = 0,1cm, delta b = 0,1 cm, delta m = 0,1 g, delta alpha = 3°, g= 9,8073 dann kommt für den Maximalfehler ein unheimlich höher Wert raus, wobei der bei diesen Werten etwa bei 0,15N liegen müsste.
Was mache ich falsch, ist die Ableitung richtig? Hoffe mir kann jemand helfen....
Wenn noch Angaben fehlen oder ich etwas übersehen habe bitte melden |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. Mai 2008 19:05 Titel: dermarkus Verfasst am: 07. Mai 2008 19:05 Titel: |
 |
|
Deine Rechnung sieht gut aus 
Was führt dich zu dem Gefühl, dass dein berechneter Fehler einen unheimlich hohen Wert habe? Wie lautet dein Endergebnis für F inclusive Fehlerangabe? |
|
 |
Steve08
Anmeldungsdatum: 27.03.2008
Beiträge: 40
|
 Steve08 Verfasst am: 10. Mai 2008 17:57 Titel: Steve08 Verfasst am: 10. Mai 2008 17:57 Titel: |
 |
|
Noch eine Frage dazu, muss ich sie senkrechten Striche als Beträge sehen oder als Klammern, genauer gesagt muss ich den 2. Wert von links in den senkrechten Strichen mit -1 multiplizieren?
Mein Maximalfehler ist bei etwa 30 und höher was nie im Leben stimmen kann. Ich habe auch schon in Excel den Winkel-Fehler ausgeschlossen indem ich die Winkel im Bogenmaß eingesetzt habe |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Mai 2008 18:10 Titel: dermarkus Verfasst am: 10. Mai 2008 18:10 Titel: |
 |
|
| Steve08 hat Folgendes geschrieben: | Noch eine Frage dazu, muss ich sie senkrechten Striche als Beträge sehen
|
Ja, das sind Betragsstriche.
| Zitat: |
Mein Maximalfehler ist bei etwa 30 und höher was nie im Leben stimmen kann. |
Da fehlt noch eine Einheit. Und sagtest du oben nicht etwas von 0,15 N?
Magst du mal übersichtlich dein Endergebnis samt Fehler aufschreiben?
also a la :  \, N) |
|
 |
Steve08
Anmeldungsdatum: 27.03.2008
Beiträge: 40
|
 Steve08 Verfasst am: 10. Mai 2008 18:55 Titel: Steve08 Verfasst am: 10. Mai 2008 18:55 Titel: |
 |
|
OK, also für folgende Wert meine Ergebnisse:
m in g : 113,5
a in mm: 125
b in mm: 125
Winkel alpha in grad: 0
delta m in g: 0,1
delta a in mm: 1
delta b in mm: 1
delta alpha in grad: 5
F in N : 1,113054775
Maximalfehler delta F = 18,7893498
Und der Maximalfehler kann niemals so hoch sein :-) |
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
 erkü Verfasst am: 10. Mai 2008 19:14 Titel: erkü Verfasst am: 10. Mai 2008 19:14 Titel: |
 |
|
Der grundsätzliche Fehler liegt darin, Rechnungen ohne physikalische Einheiten auszuführen.
Gruß erkü
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk: |
|
 |
Steve08
Anmeldungsdatum: 27.03.2008
Beiträge: 40
|
 Steve08 Verfasst am: 10. Mai 2008 19:18 Titel: Steve08 Verfasst am: 10. Mai 2008 19:18 Titel: |
 |
|
nein daran kanns nicht liegen ich habe alles auf si einheiten also m usw umgerechnet...
Vielleicht kann es ja mal einer von euch durchrechnen und mir das ergebnis für den maximalfehler mitteilen.... |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Mai 2008 20:07 Titel: Re: Partielle Ableitung - Maximalfehler dermarkus Verfasst am: 10. Mai 2008 20:07 Titel: Re: Partielle Ableitung - Maximalfehler |
 |
|
Ich habe einen Tipp und eine Vermutung für dich:
1.) Magst du mal deine Zwischenergebnisse für die Fehler angeben, die von den jeweiligen Variablen herrühren? Also die Fragezeichen in:

? Damit kannst du isolieren, woher dein überraschend großer Beitrag zum Gesamtfehler genauer herkommt.
2.) In welcher Einheit hast du das 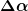 in deine Gleichung eingesetzt? Als Winkel in Grad oder als Winkel im Bogenmaß? in deine Gleichung eingesetzt? Als Winkel in Grad oder als Winkel im Bogenmaß? |
|
 |
Steve08
Anmeldungsdatum: 27.03.2008
Beiträge: 40
|
 Steve08 Verfasst am: 10. Mai 2008 21:32 Titel: Steve08 Verfasst am: 10. Mai 2008 21:32 Titel: |
 |
|
ich habe die Winkel im Bogenmaß eingesetzt auch das delta alpha
ich werde mal schrittweise rechnen und dann posten was ich herausbekommen habe |
|
 |
Steve08
Anmeldungsdatum: 27.03.2008
Beiträge: 40
|
 Steve08 Verfasst am: 12. Mai 2008 13:29 Titel: Steve08 Verfasst am: 12. Mai 2008 13:29 Titel: |
 |
|
also ich habe mal die Werte ausgerechnet und es kommt folgendes heraus:
Ich habe den Taschenrechner auf Degree und die Winkel im Bogenmaß eingesetzt:
12,26027686*0,0001+6,265001473*0,001+5,012001179*0,001+0,01717693313*PI/60
Und komme auf ein Ergebnis von 0,013.
Ich habe allerdings hier eine Lösung mit einem Wert von 0,15. Passt meine Rechnung oder ist da irgendwo ein Fehler. Als Werte habe ich die weiter oben geposteten Werte eingesetzt...
Wenn ich es mit Radiant rechne komme ich auf folgende Werte:
17,33702084*0,0001+8,859217648*0,001+7,087374119*0,001+1,77184353*PI/60
Als Ergebnis komme ich auf 0,11
0,11 liegt ja schon nahe an 0,15. Die 0,15 sind die Lösung von jemand anderem, somit kann es auch sein dass diese falsch ist.
Ich brauche auf jedenfall dringend Hilfe... |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 12. Mai 2008 14:25 Titel: dermarkus Verfasst am: 12. Mai 2008 14:25 Titel: |
 |
|
Hoppla, das kann man natürlich nicht einmal "mit degree" und einmal "mit radiant" rechnen, sondern was für ) herauskommt, darf nicht davon abhängen, wie du das rechnest. herauskommt, darf nicht davon abhängen, wie du das rechnest.
Wenn du in Grad rechnest, musst du da natürlich den Winkel in Grad einsetzen, und wenn du in rad rechnest, musst du den Winkel im Bogenmaß einsetzen.
Magst du dir das mal eindeutig überlegen, wie du das einsetzen und ausrechnen musst, und dann die vier "Fragezeichen-Terme" von oben eindeutig angeben?
Kannst du dieses Ergebnis kontrollieren, indem du dir überlegst, wieviel Prozent relativen Fehler jede einzelne der vier Variablen beisteuert? Kannst du damit grob abschätzen, ob das Ergebnis für den Gesamtfehler Sinn machen kann? |
|
 |
Steve08
Anmeldungsdatum: 27.03.2008
Beiträge: 40
|
 Steve08 Verfasst am: 12. Mai 2008 14:38 Titel: Steve08 Verfasst am: 12. Mai 2008 14:38 Titel: |
 |
|
OK das mit dem Grad und dem Radiant einsetzen ist mir klar, jedoch komme ich wenn ich die Werte im Radiant einsetze als für 45° =PI/4 und für 3° = PI/60 auf folgende Rechnung:
17,33702084*0,0001+8,859217648*0,001+7,087374119*0,001+1,77184353*PI/60
Nun meine Frage: Passt diese Rechnung für die oben genannten Werte, wenn ja dann übernehm ich diese so, weil ich nicht weis ob derjenige der die 0,15 herausbekommen hat eine andere Schwerebeschleunigung etc verwendet hat....
Vielleicht @dermarkus könntest du mal rechnen auf was du kommt und mir das posten |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 12. Mai 2008 14:48 Titel: dermarkus Verfasst am: 12. Mai 2008 14:48 Titel: |
 |
|
Ich habe mal nur den letzten Term eingetippt, da der den größten Beitrag zum Gesamtfehler liefert. Ich komme auch auf die 1,77, habe da allerdings bei mir noch eine Einheit dahinter stehen.
Auch die  bekomme ich so wie du. bekomme ich so wie du.
Wenn dein Ergebnis nicht genau mit dem eines Kollegen übereinstimmt, muss das übrigens bei einer Fehlerrechnung nicht falsch sein, sondern kann zum Beispiel einfach auch bedeuten, dass der andere seine Fehlerbalken für seine Messung anders geschätzt hat. |
|
 |
Steve08
Anmeldungsdatum: 27.03.2008
Beiträge: 40
|
 Steve08 Verfasst am: 12. Mai 2008 14:53 Titel: Steve08 Verfasst am: 12. Mai 2008 14:53 Titel: |
 |
|
ok, sowas denke ich auch, also werde ich mal meinen Maximalfehler nach der Formel der partiellen Ableitung bestimmen
Danke @dermarkus |
|
 |
beep
Gast
|
 beep Verfasst am: 29. Sep 2009 18:20 Titel: beep Verfasst am: 29. Sep 2009 18:20 Titel: |
 |
|
|
wurzel vergessen? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 29. Sep 2009 18:37 Titel: GvC Verfasst am: 29. Sep 2009 18:37 Titel: |
 |
|
Sag' mal, Steve08, ich bin mir da nicht so sicher, aber machst Du nicht einen prinzipiellen Fehler? Bei Größen, die multiplikativ verknüpft sind, was bei Deiner Bestimmungsgleichung für eine Kraft ja der Fall ist, addieren sich die relativen Fehler. Du hast aber die absoluten Fehler aufaddiert, die sich nur bei additiver Verknüpfung der fehlerbehafteten Größen zum Gesamtabsolutfehler aufsummieren. Meiner Meinung nach müsstest Du die einzelnen Relativfehler aufaddieren und erst zum Schluss mit dem Gesamtergebnis multiplizieren, um den gesamten Absolutfehler zu erhalten. Oder irre ich mich?
Allerdings passen die 0,15 N damit weder zu Deinem ersten noch zu Deinem späteren Beispiel.
Für welche Werte von a, b, m und alpha wolltest Du die Rechnung denn eigentlich machen? Und sind die jeweiligen Absolutfehler wirklich die vorgegebenen? |
|
 |
|
















