| Autor |
Nachricht |
Theodor
Gast
|
 Theodor Verfasst am: 28. Nov 2015 00:05 Titel: Partielle Ableitungen in der Physik Theodor Verfasst am: 28. Nov 2015 00:05 Titel: Partielle Ableitungen in der Physik |
 |
|
Meine Frage:
Hallo,
ich hab ein Problem mit dem Begriff der partiellen Ableitung.
1.Dazu ein Beispiel aus der Lagrange-Mechanik.
Sei A eine als Funktion gegebene Zwangsbedingung.
A heist skleronom, falls die die ZB nicht von der Zeit abhängt, bzw. ) . .
Beispielsweise für das (ebene) Pendel mit konstanter Fadenlänge l:  . Es gilt (1), daher ist A skleronom. . Es gilt (1), daher ist A skleronom.
Nun soll l zeitabhängig sein. Das ändert allerdings nichts an der partiellen Ableitung (da keine explizite Zeitabhängigkeit). (1) gilt also weiterhin und A ist immer noch skleronom! (Dabei ist die ZB ja augenscheinlich rheonom). Um die Definition zu retten müsste man A also teilweise total, teilweise partiell ableiten??
2. Die Wellengleichung: )
Die Gleichung ) ist offenbar eine Lösung von (2). Ebenso die Gleichung ist offenbar eine Lösung von (2). Ebenso die Gleichung exp(x+ct)) , für f beliebig. Setze , für f beliebig. Setze  = g(x,t) exp(-(x+ct))) , für g beliebig. Einsetzen liefert scheinbar die Erkenntis, dass alle (hinreichend guten) Funktionen (2) erfüllen! , für g beliebig. Einsetzen liefert scheinbar die Erkenntis, dass alle (hinreichend guten) Funktionen (2) erfüllen!
3.Totale Ableitung der Funktion  +t) ergibt: ergibt:
 . Hier wird abgeleitet wie bei 2., allerdings ist das Ergebnis korrekt. . Hier wird abgeleitet wie bei 2., allerdings ist das Ergebnis korrekt.
4. Als letztes ein Beispiel in dem das partielle Ableiten gut klappt:
Sei die Lagrangefunktion  (harm. Oszillator) gegeben. Für die Bewegungsgleichung folgt: (harm. Oszillator) gegeben. Für die Bewegungsgleichung folgt:

Beim vierten Beispiel ist klar deutlich warum dort keine Probleme auftreten: Keiner der dort abgeleiteten Terme weist eine implizite Abhängigkeit von der Variable auf, nach der partiell abgeleitet wird.
Wie kommt man nun zu einem konsistenten Begriff der partiellen Ableitung?
Meine Ideen:
Mir scheint als müsste von Fall zu Fall neu entschieden werden, wie mit impliziten Abhängigkeiten umgegangen werden muss.. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 28. Nov 2015 00:35 Titel: Jayk Verfasst am: 28. Nov 2015 00:35 Titel: |
 |
|
Die Frage ist nicht, wie man die partielle Ableitung konsistent definiert, sondern, was eine totale Ableitung ist.
Mathematisch ist das ganz einfach (das wird präzise in Analysis II gemacht): Eine Funktion  hänge von n Variablen ab, hänge von n Variablen ab,  \mapsto f(x_1, \dots, x_n)) . Dann wird für feste . Dann wird für feste ) eine Funktion eine Funktion ) definiert und man definiert definiert und man definiert
 := f_{x_2, \dots , x_n}'(x_1))
über die ganz normale Ableitung aus Analysis I.
(Anmerkung: die Notation setzt natürlich voraus, daß man sich darüber einig ist, daß 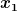 der Name des ersten Arguments ist, d.h. es findet eigentlich eine Doppelbelegung für den abstrakten Namen des ersten Arguments und den Wert, an dem man auswertet, statt) der Name des ersten Arguments ist, d.h. es findet eigentlich eine Doppelbelegung für den abstrakten Namen des ersten Arguments und den Wert, an dem man auswertet, statt)
Mathematisch ist damit alles gesagt, der Begriff "totale Ableitung" wird in dieser Form "nur" in Anwendungsgebieten wie Physik+Ingenieurwissenschaften verwendet. Der Grund ist, daß sowohl Funktionen als auch Variablen dazu verwendet werden, um physikalische Größen zu beschreiben. Die physikalischen Zusammenhänge sind eine Sache, ihre mathematische Beschreibung eine andere. Beispiel: Es ist gleichgültig, ob man sagt, die Fläche eines Kreises hänge von Radius oder Durchmesser ab. Es ist eben  und und  . Es macht aber mathematisch einen Unterschied, ob man . Es macht aber mathematisch einen Unterschied, ob man

 = \pi x^2)
oder

 = \frac \pi 4 x^2 = \frac 1 4 A_r(x))
betrachtet. Nun kann man aber 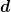 , statt als Variable, auch als Funktion von r auffassen, , statt als Variable, auch als Funktion von r auffassen,  = 2 r) . Insofern definiert man sinnvollerweise . Insofern definiert man sinnvollerweise
)\,d'(r) = (A_d \circ d)'(r)) , ,
was gleich ist mit ) . Das heißt, man will eine gewisse Unabhängigkeit bzw. Flexibilität mit den unabhängigen Variablen erhalten. . Das heißt, man will eine gewisse Unabhängigkeit bzw. Flexibilität mit den unabhängigen Variablen erhalten.
Das ist im Prinzip das einfachste Beispiel. Hast Du nun eine Funktion ) , die von x und t abhängt, dann kannst Du Dich später umentscheiden, , die von x und t abhängt, dann kannst Du Dich später umentscheiden, ) selbst als Funktion von t aufzufassen, und definierst selbst als Funktion von t aufzufassen, und definierst
, t) = \frac{\partial f}{\partial t} (x(t), t) + \frac{\partial f}{\partial x} (x(t), t) \cdot \frac{d x}{d t}(t)) . .
(das erste Gleichheitszeichen ist mehr oder weniger eine Definition bzw. eine Erklärung einer Notation, das zweite ist eine echte Gleichheit, da links eine ganz gewöhnliche Ableitung einer Komposition steht)
Das ist offensichtlich keine Größe, die nur von der Funktion f abhängt, sondern eine, die von der Bedeutung der Variablen abhängt. |
|
 |
Theodor
Gast
|
 Theodor Verfasst am: 28. Nov 2015 02:02 Titel: Theodor Verfasst am: 28. Nov 2015 02:02 Titel: |
 |
|
Ich verstehe nicht ganz inwiefern mir das weiter helfen soll, bzw. worauf du hinaus willst  |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 28. Nov 2015 03:48 Titel: Jayk Verfasst am: 28. Nov 2015 03:48 Titel: |
 |
|
1. Die partielle Ableitung ist mathematisch präzise definiert, Definition steht oben (und in jedem Buch/Skript über Analysis II).
1.1. Das setzt allerdings voraus, daß man sich im Klaren ist, welche Funktion man überhaupt vor sich hat. Zu einer Funktion gehört insbesondere ein Definitionsbereich, also einer Liste der Argumente mit infrage kommenden Werten. Eine Gleichung wie 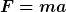 ist physikalisch verständlich, aber definiert noch keine Funktion und kann daher noch nicht mit Methoden der Analysis bearbeitet werden. ist physikalisch verständlich, aber definiert noch keine Funktion und kann daher noch nicht mit Methoden der Analysis bearbeitet werden.
2. Das gilt nicht für die totale Ableitung. Hier muß man etwas dazu interpretieren, um ihr einen Sinn zu geben (im Allgemeinen steht dieselbe Bezeichnung für dieselbe physikalische Größe, jedoch für zwei mathematisch unterschiedliche Dinge: die Variable einer Funktion und eine Funktion, die von einer oder mehrerer der anderen Variablen der ersten Funktion abhängt).
Wenn Du einfach nur Dinge wie  schreibst, wirst Du allerdings weiter im Dunkeln tappen. Abgeleitet wird eine Funktion nach einer Variablen, also ist es Deine Aufgabe, festzulegen, was die Variablen sind und welche Variablen bloß durch eine implizite Abhängigkeit realisiert sind: schreibst, wirst Du allerdings weiter im Dunkeln tappen. Abgeleitet wird eine Funktion nach einer Variablen, also ist es Deine Aufgabe, festzulegen, was die Variablen sind und welche Variablen bloß durch eine implizite Abhängigkeit realisiert sind:  = \frac 1 2 m v^2 - V(q)) . Nicht richtig wäre . Nicht richtig wäre =\frac 1 2 m v^2 - V) (es würde schon Sinn ergeben, aber das ist einfach nicht, was man meint). Wenn eine implizite Abhängigkeit vorliegt, geht diese in die totale Ableitung ein. (es würde schon Sinn ergeben, aber das ist einfach nicht, was man meint). Wenn eine implizite Abhängigkeit vorliegt, geht diese in die totale Ableitung ein.
Für die Wahl gibt es kein Patentrezept, sondern Du mußt mitdenken.
zu (1): Eine Zwangsbedingung ist eine Gleichung, die den Konfigurationsraum beschreibt. Dafür ist 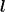 als Konstante zu verstehen (danach wird gar nicht abgeleitet!) und x,y,t als Koordinaten. Und skleronom heißt, daß der Konfigurationsraum zeitunabhängig ist. Wenn Du nun stattdessen l zeitabhängig machst, hast Du einen zeitabhängigen Konfigurationsraum und als Konstante zu verstehen (danach wird gar nicht abgeleitet!) und x,y,t als Koordinaten. Und skleronom heißt, daß der Konfigurationsraum zeitunabhängig ist. Wenn Du nun stattdessen l zeitabhängig machst, hast Du einen zeitabhängigen Konfigurationsraum und  = x^2 + y^2 - l(t)^2) ist zeitabhängig (wie Du siehst: Es ist wichtig, festzulegen, was die Variablen sind!). ist zeitabhängig (wie Du siehst: Es ist wichtig, festzulegen, was die Variablen sind!).
Es ist offensichtlich nicht dasselbe, ob  eine Konstante oder eine Konstante oder ) eine Funktion ist. eine Funktion ist.
zu (4): Die ELG lautet, ausführlich aufgeschrieben:
) ist eine Funktion von q und v, ist eine Funktion von q und v, ) eine Funktion von t; die Gleichbenennung der Variablen q und der Funktion q ist physikalischer, nicht mathematischer, Natur! eine Funktion von t; die Gleichbenennung der Variablen q und der Funktion q ist physikalischer, nicht mathematischer, Natur!
, \dot q(t)) \right] = \frac{\partial L}{\partial q} (q(t), \dot q(t)))
Die Notation verwende ich folgendermaßen:
 heißt, daß der nachfolgende Teil (als Komposition) als Funktion allein von t zu verstehen ist und danach abgeleitet wird. heißt, daß der nachfolgende Teil (als Komposition) als Funktion allein von t zu verstehen ist und danach abgeleitet wird.
, \dot q(t))) heißt, daß L nach der zweiten Variablen partiell abgeleitet wird und die entstehende Funktion bei heißt, daß L nach der zweiten Variablen partiell abgeleitet wird und die entstehende Funktion bei , v=\dot q(t)) ausgewertet wird. ausgewertet wird.
(das heißt, ich unterscheide in der Notation dazwischen, ob die Funktion mit im Zähler oder dahinter aufgeführt wird)
Zu (3) ist nichts zu sagen.
(2) ist so einfach nicht richtig. Die allgemeinste Lösung der Wellengleichung ist  = f(x+ct) + g(x-ct)) für C²-Funktionen f,g (die jeweils von einer Variablen abhängen). Du kannst ja mal vorrechnen, wie Du darauf kommst, daß das von Dir Angegebene eine Lösung wäre. Möglicherweise hast Du es Dir aber auch einfach falsch gemerkt oder falsch abgeschrieben, denn wenn man für C²-Funktionen f,g (die jeweils von einer Variablen abhängen). Du kannst ja mal vorrechnen, wie Du darauf kommst, daß das von Dir Angegebene eine Lösung wäre. Möglicherweise hast Du es Dir aber auch einfach falsch gemerkt oder falsch abgeschrieben, denn wenn man ) durch durch ) ersetzt, ist es richtig. Das von Dir dann definierte f ist aber nicht von diesem Typ; es sei denn, g ist ebenfalls vom Typ ersetzt, ist es richtig. Das von Dir dann definierte f ist aber nicht von diesem Typ; es sei denn, g ist ebenfalls vom Typ ) , und dann stimmt die Aussage auch. , und dann stimmt die Aussage auch.
Es ist natürlich okay, wenn man der Übersichtlichkeit halber die Abhängigkeiten nicht mitführt. Das sollte aber erst machen, wenn man es verstanden hat, was Du offensichtlich noch nicht hast. |
|
 |
Theodor
Gast
|
 Theodor Verfasst am: 28. Nov 2015 15:45 Titel: Theodor Verfasst am: 28. Nov 2015 15:45 Titel: |
 |
|
Das heißt also für  = g (t)*t + x(t) gilt \frac {\partial f}{\partial t} = t \frac {\partial g(t)}{\partial t} + g (t) ) , bzw. , bzw.  = g (t)*t + x(t); \frac {\partial f}{\partial t} = t \frac {\partial g(t)}{\partial t} + g (t) + \frac {\partial x(t)}{\partial t}) , wobei die partiellen Ableitungen von g und x den "normalen" entprechen? , wobei die partiellen Ableitungen von g und x den "normalen" entprechen? |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 28. Nov 2015 18:10 Titel: Jayk Verfasst am: 28. Nov 2015 18:10 Titel: |
 |
|
| Theodor hat Folgendes geschrieben: | | wobei die partiellen Ableitungen von g und x den "normalen" entprechen? |
Ja, ganz richtig. 
Obwohl man sagen muß, daß dieses Beispiel sehr künstlich wirkt, wie auch mein Beispiel von oben zur Kreisfläche. So würde es nie jemand aufschreiben (denn es ist dusselig, eine Abhängigkeit von x "bereitzustellen", die gar nicht vorkommt, und gleichzeitig eine Funktion x(t) zu haben), aber beide Beispiele sind ganz gut, um zu zeigen, daß es darauf ankommt, was die Variablen sind.
Um das nochmal an Deinem Beispiel zu erklären:
 = g(t)\,t + x(t)) hat hat  wie von Dir angegeben und wie von Dir angegeben und  ; allerdings hätte man auch einfach ; allerdings hätte man auch einfach  = g(t)\,t+x(t)) schreiben können, in diesem Sinne stimmt die "ganz normale" Ableitung schreiben können, in diesem Sinne stimmt die "ganz normale" Ableitung  mit der partiellen überein. mit der partiellen überein.
 = g(t)\,t + x) hat hat 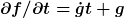 und und  . Wenn bekannt ist, daß x gleichzeitig in einem physikalischen/anschaulichen Sinn eine t-Abhängigkeit hat, dann würde man . Wenn bekannt ist, daß x gleichzeitig in einem physikalischen/anschaulichen Sinn eine t-Abhängigkeit hat, dann würde man  den Ausdruck nennen, den Du im ersten Fall als partielle Ableitung ausgerechnet hast. den Ausdruck nennen, den Du im ersten Fall als partielle Ableitung ausgerechnet hast.
Unter Umständen passiert es, daß einfach

geschrieben wird. Dann mußt Du herausfinden, ob der erste oder der zweite Fall gemeint ist. Vernünftig wäre, den zweiten Fall anzunehmen, ansonsten würde man vermutlich  = g(t)\,t+x(t)) schreiben. Das heißt, f ist eine Funktion von zwei Variablen. Wie die partiellen Ableitungen berechnet werden, sollte damit klar sein. Wenn nun ein Ausdruck schreiben. Das heißt, f ist eine Funktion von zwei Variablen. Wie die partiellen Ableitungen berechnet werden, sollte damit klar sein. Wenn nun ein Ausdruck  auftaucht, so heißt das, daß einige der übrigen Abhängigkeiten (in diesem Fall also die Abhängigkeit von x) eliminiert werden, indem man statt x eine Funktion x(t) einsetzt. Man bekommt also durch Komposition eine neue Funktion, die nur von t abhängt, und deren Ableitung ist die totale Ableitung df/dt. auftaucht, so heißt das, daß einige der übrigen Abhängigkeiten (in diesem Fall also die Abhängigkeit von x) eliminiert werden, indem man statt x eine Funktion x(t) einsetzt. Man bekommt also durch Komposition eine neue Funktion, die nur von t abhängt, und deren Ableitung ist die totale Ableitung df/dt.
Wenn es zu Verwirrungen kommen kann, kann man auch so etwas wie
_{p, V})
schreiben, was dann angibt, welche Variablen konstant gehalten werden. Das heißt, die Schreibweise deutet an, daß man S als Funktion von E,p,V aufzufassen hat und diese partiell nach E ableiten soll. Diese Schreibweise wird in der Thermodynamik sehr oft verwendet. |
|
 |
Theodor
Gast
|
 Theodor Verfasst am: 01. Dez 2015 00:15 Titel: Theodor Verfasst am: 01. Dez 2015 00:15 Titel: |
 |
|
Ok vielen Dank bereits an dieser Stelle!
Noch eine Frage zu einer Herleitung aus dem Demtröder:
books.google.de /books?id=LmQiBgAAQBAJ&pg=PA118&lpg=PA118&dq#v=onepage&q&f=false
Wie funktioniert der Schritt von 4.5 zu 4.6a? Die Gleichung 4.5 erhält man doch nur, wenn Ekin = const ist. Für den allgemeinen (4.6a) Fall ist aber doch Ekin und damit k räumlich variabel. Sollte man nicht also }{\partial x^2} = \frac{\partial }{\partial x}e^{i/\hbar(k(x)x-Et} ( k(x) + \frac{\partial k}{\partial x}) = e^{i/\hbar(k(x)x-Et}(k(x) + \frac{\partial k}{\partial x} +\frac{\partial ^2k}{\partial x^2})) erhalten? erhalten? |
|
 |
Theodor
Gast
|
 Theodor Verfasst am: 01. Dez 2015 10:41 Titel: Theodor Verfasst am: 01. Dez 2015 10:41 Titel: |
 |
|
Korrektur : Das Ergebnis der Differentiation ist  x -Et)}(\frac {\partial ^2 k}{\partial x^2} + (\frac {\partial k}{\partial x})^2) ) |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 02. Dez 2015 13:37 Titel: Jayk Verfasst am: 02. Dez 2015 13:37 Titel: |
 |
|
| Zitat: | | Für den allgemeinen (4.6a) Fall ist aber doch Ekin und damit k räumlich variabel |
Achtung, dort wird induktiv vorgegangen: Ein allgemeines physikalisches Gesetz (die Schrödingergleichung) wird aus einer sehr speziellen Situation "hergeleitet". Diese sehr spezielle Situation ist  = \psi(x) e^{- i \omega t}) . Dafür sind Impuls, Wellenvektor, Kreisfrequenz und kinetische Energie einfach Zahlen, unabhängig vom Ort. . Dafür sind Impuls, Wellenvektor, Kreisfrequenz und kinetische Energie einfach Zahlen, unabhängig vom Ort.
Anmerkung zur Physik:
Im allgemeinen Fall kann man nicht einfach von einem Impuls oder einer kinetischen Energie sprechen, auch nicht von einer ortsabhängigen. Man kann jeweils von einem Erwartungswert oder einer Unschärfe oder einer Wahrscheinlichkeitsverteilung sprechen. Dafür führt man dann Operatoren ein, z.B. den Impulsoperator  , so daß man etwa den Erwartungswert der i-ten Impulskomponente für eine gegebene Wellenfunktion durch , so daß man etwa den Erwartungswert der i-ten Impulskomponente für eine gegebene Wellenfunktion durch
^*\,\frac{\partial \psi}{\partial x_i} (\vec x))
bekommt. Im allgemeinen kann man psi(x) durch
 = \frac{1}{(2 \pi)^3} \int_{\mathbb{R}^3} d^3 k\,\hat \psi (\vec k)\,e^{i \vec k \cdot \vec x})
darstellen (Fouriertransformation) und somit }{(2 \pi)^3} \right\vert^2) als Wahrscheinlichkeitsdichte interpretieren. Es ist allerdings eben nicht möglich, jedem Ort einen Wellenvektor k oder einen Impuls p zuzuweisen. als Wahrscheinlichkeitsdichte interpretieren. Es ist allerdings eben nicht möglich, jedem Ort einen Wellenvektor k oder einen Impuls p zuzuweisen. |
|
 |
Theodor
Gast
|
 Theodor Verfasst am: 02. Dez 2015 23:15 Titel: Theodor Verfasst am: 02. Dez 2015 23:15 Titel: |
 |
|
Ok ich sehe gerade auch, dass eine enstprechend modifizierte "ebene" Welle (mit  = p(x) = \sqrt{2m (E-V(x))}) ) gar keine Lösung der SGL ist. ) gar keine Lösung der SGL ist.
Dann nochmal vielen Dank |
|
 |
|
|

















