| Autor |
Nachricht |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 300
|
 Corbi Verfasst am: 21. Dez 2018 12:20 Titel: Wie wird die Trägheit in der modernen Physik erklärt Corbi Verfasst am: 21. Dez 2018 12:20 Titel: Wie wird die Trägheit in der modernen Physik erklärt |
 |
|
Meine Frage:
In der klassischen Mechanik wirkt eine Trägheitskraft wenn ein Bezugssystem relativ zum absoluten Raum beschleunigt. Spätestens seit der SRT wurde aber das merkwürdige Konzept des absoluten Raums verworfen. Aber worauf bezieht sich meine Beschleunigung dann? Relativ zu welchem Bezugssystem beschleunige ich, wenn es mich beim Autofahren in den Sitz drückt?
Oder anders ausgedrückt: wie wird Newtons Eimerexperiment mit der modernen Physik erklärt?
Meine Ideen:
Ernst Mach sagt, dass sich die Beschleunigung auf alle umliegenden Massen Bezieht (Machsches Prinzip). Ist diese Idee in der ART realisiert? Oder liefert die ART garkeine Erklärung der Trägheit?
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 21. Dez 2018 21:22 Titel: Re: Wie wird die Trägheit in der modernen Physik erklärt index_razor Verfasst am: 21. Dez 2018 21:22 Titel: Re: Wie wird die Trägheit in der modernen Physik erklärt |
 |
|
| Corbi hat Folgendes geschrieben: | Meine Frage:
In der klassischen Mechanik wirkt eine Trägheitskraft wenn ein Bezugssystem relativ zum absoluten Raum beschleunigt. Spätestens seit der SRT wurde aber das merkwürdige Konzept des absoluten Raums verworfen. Aber worauf bezieht sich meine Beschleunigung dann?
|
In beiden Theorien ist Beschleunigung ein Maß für die Abweichung von einer geradlinig gleichförmigen Bewegung. Diese Größe ist nicht relativ zu irgendwas, sondern absolut. Die genaue Quantifizierung dieser Größe ist jeweils unterschiedlich und hängt von der Struktur der Raumzeit ab, aber das Konzept ist mehr oder weniger dasselbe. Der absolute Raum spielt dabei m.E. keine besondere Rolle.
| Zitat: |
Relativ zu welchem Bezugssystem beschleunige ich, wenn es mich beim Autofahren in den Sitz drückt?
|
Relativ zu allen Bezugssystemen. Eine andere Frage ist, wie sich die Größe der Beschleunigung eines Teilchens in den Koordinaten des jeweiligen Bezugssystems ausdrückt. Inertialsysteme sind dadurch charakterisiert, daß

genau dann wenn die Bewegung geradlinig-gleichförmig, also unbeschleunigt ist. In einem Nichtinertialsystem ist dies nicht unbedingt der Fall. Anders ausgedrückt ist die (absolute) Beschleunigung in Nicht-Inertialsystemen nicht mit der zweiten Ableitung der Ortskoordinaten nach der Zeit identisch.
| Zitat: |
Oder anders ausgedrückt: wie wird Newtons Eimerexperiment mit der modernen Physik erklärt?
|
Da bei der Erklärung dieses Phänomens keine relativistischen Effekte eine Rolle spielen, würde ich behaupten die Erklärung lautet nicht wesentlich anders als in der Newtonschen Mechanik.
| Zitat: |
Meine Ideen:
Ernst Mach sagt, dass sich die Beschleunigung auf alle umliegenden Massen Bezieht (Machsches Prinzip). Ist diese Idee in der ART realisiert?
|
Mehr oder weniger. Eine moderne Auffassung ist, daß sich das Machsche Prinzip in gewisser Weise in der Formulierung der Einsteinschen Feldgleichungen als Anfangswertproblem wieder finden läßt. Viel kann ich dir darüber nicht erzählen, aber mein oberflächlicher Eindruck ist, daß dies eine ganz passable Interpretation ist, wenn auch mit Sicherheit nicht wörtlich diejenige, die Mach im Sinn hatte.
|
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 300
|
 Corbi Verfasst am: 22. Dez 2018 00:04 Titel: Corbi Verfasst am: 22. Dez 2018 00:04 Titel: |
 |
|
| Zitat: | | "Da bei der Erklärung dieses Phänomens keine relativistischen Effekte eine Rolle spielen, würde ich behaupten die Erklärung lautet nicht wesentlich anders als in der Newtonschen Mechanik." |
In der Newtonschen Mechanik wird das Problem durch die Einführung eines absoluten Raums gelöst. Also muss es in der modernen Physik ja eine andere Erklärung geben.
| Zitat: |
"In beiden Theorien ist Beschleunigung ein Maß für die Abweichung von einer geradlinig gleichförmigen Bewegung. Diese Größe ist nicht relativ zu irgendwas, sondern absolut. Die genaue Quantifizierung dieser Größe ist jeweils unterschiedlich und hängt von der Struktur der Raumzeit ab, aber das Konzept ist mehr oder weniger dasselbe. Der absolute Raum spielt dabei m.E. keine besondere Rolle." |
Erst sagst du die Beschleunigung ist absolut und dann sagst du der absolute Raum spiele keine besondere Rolle? Die Gesamte Newton-Mechanik basiert auf der Annahme eines absoluten Bezugssystems. Die Abweichung von der geradlinig-gleichförmigen Bewegung bezieht sich bei Newton immer auf den absoluten Raum. Stell dir mal zwei Autos vor, die nebeneinander auf der Autobahn genau gleich schnell beschleunigen. Aus der Sicht des einen Autos, ist das andere Auto dann in Ruhe (bewegt sich also geradlinig und gleichförmig) und trotzdem wirkt in diesem Auto eine Trägheitskraft, da es nach Newton relativ zum absoluten Raum beschleunigt ist.
Einstein ging es in der ART auch genau darum, diese absolute Natur der Beschleunigung zu beseitigen.
Also wodurch wird dieses absolute Bezugsystem in der modernen Physik ersetzt?
Wenn ich in einem Raumschiff irgendwo weit draussen im All bin und dieses Raumschiff beschleunigt nun dann spüre ich eine Trägheitskraft. Aber relativ zu was beschleunigt das Raumschiff? Es wird ja irgendeine Art von Bezugssystem benötigt, die die gleichförmige von der beschleunigten Bewegung unterscheidet
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 22. Dez 2018 00:48 Titel: DrStupid Verfasst am: 22. Dez 2018 00:48 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | | Also wodurch wird dieses absolute Bezugsystem in der modernen Physik ersetzt? |
Durch ein lokal frei fallendes Bezugssystem.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Dez 2018 08:29 Titel: index_razor Verfasst am: 22. Dez 2018 08:29 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | | Zitat: | | "Da bei der Erklärung dieses Phänomens keine relativistischen Effekte eine Rolle spielen, würde ich behaupten die Erklärung lautet nicht wesentlich anders als in der Newtonschen Mechanik." |
In der Newtonschen Mechanik wird das Problem durch die Einführung eines absoluten Raums gelöst. Also muss es in der modernen Physik ja eine andere Erklärung geben.
|
Nein, in der Newtonschen Mechanik wird das Problem, so wie jedes andere Problem der Bewegung träger Körper, durch die Betrachtung der wirkenden Kräfte und die Berücksichtigung der herrschenden Anfags- bzw. Randbdingungen gelöst. Wie kommst du darauf ein rotierender Eimer benötige irgendwelche theoretischen Spezialkonzepte?
| Zitat: |
| Zitat: |
"In beiden Theorien ist Beschleunigung ein Maß für die Abweichung von einer geradlinig gleichförmigen Bewegung. Diese Größe ist nicht relativ zu irgendwas, sondern absolut. Die genaue Quantifizierung dieser Größe ist jeweils unterschiedlich und hängt von der Struktur der Raumzeit ab, aber das Konzept ist mehr oder weniger dasselbe. Der absolute Raum spielt dabei m.E. keine besondere Rolle." |
Erst sagst du die Beschleunigung ist absolut und dann sagst du der absolute Raum spiele keine besondere Rolle? Die Gesamte Newton-Mechanik basiert auf der Annahme eines absoluten Bezugssystems.
|
Beschleunigung ist nicht deshalb absolut, weil sie sich auf den absoluten Raum bezieht, sondern weil sie überhaupt keinen Bezug benötigt -- weder die Angabe eines Beobachters noch die Festlegung eines Bezugssystems.
Diese Eigenschaft teilt sie mit dem "Raum" in der Newtonschen Mechanik. Dieser ist definiert durch die Menge aller Ereignisse zu einem festen absoluten Zeitpunkt, also ebenfalls unabhängig vom Beobachter.
Also gibt es in der Newtonschen Physik sowohl einen absoluten Raum, als auch eine absolute Beschleunigung. Aber die Beschleunigung verdankt ihre Absolutheit nicht der des Raumes. Deswegen bleibt die Beschleunigung in der Relativitätstheorie absolut, auch wenn der absolute Raum wegfällt.
| Zitat: |
Die Abweichung von der geradlinig-gleichförmigen Bewegung bezieht sich bei Newton immer auf den absoluten Raum.
|
Das stimmt nicht. Genauso könntest du behaupten in der euklidischen Geometrie beziehe sich Geradheit auf ein absolutes kartesisches Koordinatensystem. Geradheit ist eine geometrisch absolute Eigenschaft. Geradlinig-gleichförmig bedeutet nichts anderes als "gerade in Raum und Zeit".
| Zitat: |
Stell dir mal zwei Autos vor, die nebeneinander auf der Autobahn genau gleich schnell beschleunigen. Aus der Sicht des einen Autos, ist das andere Auto dann in Ruhe (bewegt sich also geradlinig und gleichförmig) und trotzdem wirkt in diesem Auto eine Trägheitskraft, da es nach Newton relativ zum absoluten Raum beschleunigt ist.
|
Im letzten Beitrag schrieb ich es bereits: "In Ruhe" impliziert nur in Inertialsystemen "geradlinig-gleichförmig". In Nicht-Inertialsystemen kann ein Körper relativ zu einem bestimmten Bezugspunkt ruhen und trotzdem absolut beschleunigt sein.
| Zitat: |
Einstein ging es in der ART auch genau darum, diese absolute Natur der Beschleunigung zu beseitigen.
|
Nein, darum ging es ihm nicht und das tat er auch nicht. Die Beschleunigung ist in der ART die kovariante Ableitung der Vierergeschwindigkeit entlang der Weltlinie. Das ist keine bezugssystemabhängige Größe.
| Zitat: |
Also wodurch wird dieses absolute Bezugsystem in der modernen Physik ersetzt?
|
Es gibt kein absolutes Bezugssystem in der Newtonschen Mechanik. Es existiert eine absolute Zeit und ein absoluter Raum. Aber beide erlauben noch nicht die Konstruktion eines absoluten Bezugssystems oder die Definition absoluter Ruhe oder Bewegung.
| Zitat: |
Wenn ich in einem Raumschiff irgendwo weit draussen im All bin und dieses Raumschiff beschleunigt nun dann spüre ich eine Trägheitskraft. Aber relativ zu was beschleunigt das Raumschiff?
|
Es beschleunigt. Punkt. Mathematisch bedeutet das, daß die kovariante Ableitung
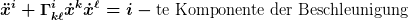
nicht den Nullvektor ergibt. Die Größen  heißen "Koeffizienten des affinen Zusammenhangs". Sie definieren in jeder Geometrie -- egal ob du eine gekrümmte Fläche, die Einsteinsche oder die Newtonsche Raumzeit betrachtest -- den Begriff der "Geradheit" oder, was äquivalent ist, der "Parallelverschiebung". heißen "Koeffizienten des affinen Zusammenhangs". Sie definieren in jeder Geometrie -- egal ob du eine gekrümmte Fläche, die Einsteinsche oder die Newtonsche Raumzeit betrachtest -- den Begriff der "Geradheit" oder, was äquivalent ist, der "Parallelverschiebung".
Wenn du nun ein Inertialsystem wählst, um die Bewegung zu beschreiben, erkennst du die Beschleunigung des Raumschiffs daran, daß die zweite Ableitung des Ortes nach der Zeit nicht verschwindet, also gilt (und zwar nur in Inertialsystemen)

Das bedeutet nur, daß Inertialsysteme dadurch ausgezeichnet sind, daß alle Größen  sind. In Nicht-Inertialsystemen gilt dies nicht, d.h. es kann auch dann eine Beschleunigung vorliegen, wenn sind. In Nicht-Inertialsystemen gilt dies nicht, d.h. es kann auch dann eine Beschleunigung vorliegen, wenn  . .
Wenn man noch ein bißchen weiter darüber nachdenkt, erkennt man, daß  genau die Trägheitskräfte in diesem System beschreiben. (Da sie in Inertialsystemen verschwinden, sind dies also genau die Systeme, in denen keine Trägheitskräfte existieren.) genau die Trägheitskräfte in diesem System beschreiben. (Da sie in Inertialsystemen verschwinden, sind dies also genau die Systeme, in denen keine Trägheitskräfte existieren.)
| Zitat: |
Es wird ja irgendeine Art von Bezugssystem benötigt, die die gleichförmige von der beschleunigten Bewegung unterscheidet |
Du kannst jedes Bezugssystem verwenden und in jedem Bezugssystem erhältst du dieselbe Antwort, daß das Raumschiff beschleunigt ist. Das ist in der Newtonschen Mechanik genau so wie in der ART.
|
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 300
|
 Corbi Verfasst am: 22. Dez 2018 15:32 Titel: Corbi Verfasst am: 22. Dez 2018 15:32 Titel: |
 |
|
| Zitat: | | Nein, in der Newtonschen Mechanik wird das Problem, so wie jedes andere Problem der Bewegung träger Körper, durch die Betrachtung der wirkenden Kräfte und die Berücksichtigung der herrschenden Anfags- bzw. Randbdingungen gelöst. Wie kommst du darauf ein rotierender Eimer benötige irgendwelche theoretischen Spezialkonzepte? |
Darauf bin nicht ich gekommen sondern Newton selbst. Er führt dieses Gedankenexperiment an um sein absolutes Bezugssystem zu begründen. (Google mal nach Newtons Eimerexperiment). Und genau da setzt ja auch das Machsche Prinzip an. Es ersetzt die Vorstellung des absoluten Bezugssystems durch ein Bezugssystem das durch die umgebenden Masse auf irgendeine Art und Weise hervorgerufen wird.
| Zitat: | | Aber die Beschleunigung verdankt ihre Absolutheit nicht der des Raumes. |
. Das stimmt so nicht. Auch auf Wikipedia steht: "Der absolute Raum und die absoluten Zeit bilden bei Newton die Grundlage der von ihm begründeten Klassischen Mechanik und in der Folge auch die der Klassischen Physik. Demnach finden alle absoluten Bewegungen relativ zum absoluten Raum statt." (Quelle: https://de.wikipedia.org/wiki/Absoluter_Raum)
| Zitat: | | Es gibt kein absolutes Bezugssystem in der Newtonschen Mechanik. Es existiert eine absolute Zeit und ein absoluter Raum. Aber beide erlauben noch nicht die Konstruktion eines absoluten Bezugssystems oder die Definition absoluter Ruhe oder Bewegung. |
Was soll den ein Bezugssystem anderes sein als ein Raum? Ein Bezugssystem ist immer ein Koordinatensystem und genau das ist auch der Raum selbst in der Physikalischen Betrachtung.
| Zitat: | Einstein ging es in der ART auch genau darum, diese absolute Natur der Beschleunigung zu beseitigen.
Nein, darum ging es ihm nicht und das tat er auch nicht. Die Beschleunigung ist in der ART die kovariante Ableitung der Vierergeschwindigkeit entlang der Weltlinie. Das ist keine bezugssystemabhängige Größe. |
Einstein schreibt in seinem Buch (Über die spezielle und die allgemeine Relativitätstheorie) selbst: ...Wir fühlen uns daher zunächst genötigt, entgegen dem Allgemeinen Relativitätsprinzip der ungleichförmigen Bewegung eine Art absolute physikalische Realität zuzusprechen. Im folgenden werden wir aber bald sehen, dass dieser Schluss nicht stichhaltig ist." Deine Ansicht, dass die Beschleunigung in der ART also auch eine absolute Beschleunigung ist teilt Einstein offensichtlich nicht.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Dez 2018 17:41 Titel: index_razor Verfasst am: 22. Dez 2018 17:41 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | | Zitat: | | Nein, in der Newtonschen Mechanik wird das Problem, so wie jedes andere Problem der Bewegung träger Körper, durch die Betrachtung der wirkenden Kräfte und die Berücksichtigung der herrschenden Anfags- bzw. Randbdingungen gelöst. Wie kommst du darauf ein rotierender Eimer benötige irgendwelche theoretischen Spezialkonzepte? |
Darauf bin nicht ich gekommen sondern Newton selbst. Er führt dieses Gedankenexperiment an um sein absolutes Bezugssystem zu begründen. (Google mal nach Newtons Eimerexperiment). Und genau da setzt ja auch das Machsche Prinzip an. Es ersetzt die Vorstellung des absoluten Bezugssystems durch ein Bezugssystem das durch die umgebenden Masse auf irgendeine Art und Weise hervorgerufen wird.
|
Meines Wissens wollte Newton gerade für die Absolutheit der Beschleunigung argumentieren, nicht für die Existenz eines absoluten Bezugssystems. Aber genau weiß ich es zugegebenermaßen nicht. Es spielt aber m.E. keine Rolle, denn in der Newtonschen Mechanik gilt das Galileische Relativitätsprinzip. Ein absolutes Bezugssystem würde diesem Prinzip ja nun drastisch widersprechen.
| Zitat: |
| Zitat: | | Aber die Beschleunigung verdankt ihre Absolutheit nicht der des Raumes. |
. Das stimmt so nicht. Auch auf Wikipedia steht: "Der absolute Raum und die absoluten Zeit bilden bei Newton die Grundlage der von ihm begründeten Klassischen Mechanik und in der Folge auch die der Klassischen Physik. Demnach finden alle absoluten Bewegungen relativ zum absoluten Raum statt." (Quelle: https://de.wikipedia.org/wiki/Absoluter_Raum)
|
Die Schlußfolgerung im zweiten Satz ist bestenfalls vage und unklar.
Eine Präzisierung von "Bewegung relativ zum absoluten Raum" führt m.E. schnell auf das Konzept der absoluten Ruhe, was nicht zuletzt im Lichte des Relativitätsprinzips völlig unnötig ist. Aber da du es zitiert hast, kannst du mir sicher erklären was genau mit "allen absoluten Bewegungen" gemeint ist und wie der Begriff der "Bewegung relativ zum absoluten Raum" das Problem umgeht, eine Definition von absoluter Ruhe zu ermöglichen, die wegen des Relativitätsprinzips eben "prinzipiell" nicht feststellbar ist.
Ein mit dem Relativitätsprinzip verträgliches Konzept des absoluten Raumes gestattet nicht ohne weiteren Bezug zu definieren, ob zwei Ereignisse zu verschiedenen absoluten Zeitpunkten am selben Ort stattfinden. Damit kann man nicht mehr ohne Bezug definieren ob der Körper ruht oder bewegt ist. Also existiert auch keine Bewegung "relativ" zum absoluten Raum. Man kann aber immer noch ohne Bezug feststellen ob der Körper beschleunigt ist oder nicht, einfach indem man die Geradheit seiner Weltlinie beurteilt.
| Zitat: |
| Zitat: | | Es gibt kein absolutes Bezugssystem in der Newtonschen Mechanik. Es existiert eine absolute Zeit und ein absoluter Raum. Aber beide erlauben noch nicht die Konstruktion eines absoluten Bezugssystems oder die Definition absoluter Ruhe oder Bewegung. |
Was soll den ein Bezugssystem anderes sein als ein Raum? Ein Bezugssystem ist immer ein Koordinatensystem und genau das ist auch der Raum selbst in der Physikalischen Betrachtung.
|
Der Raum ist kein Koordinatensystem, sondern eine Menge von Punkten oder noch besser: von gleichzeitigen Ereignissen in der Raumzeit. (Da bei Newton die Zeit absolut ist, ist es nach dieser Definition also auch der Raum.) Dieser hat, wenn er leer ist, normalerweise Euklidische Struktur, d.h. es handelt sich um einen affinen Raum mit innerem Produkt auf dem Tangentialraum.
Ein Bezugssystem hingegen ist eine spezielle Klasse von Koordinatensystemen auf der Raumzeit, bestehend aus einer Zeitachse und 3 Raumachsen.
| Zitat: |
| Zitat: | Einstein ging es in der ART auch genau darum, diese absolute Natur der Beschleunigung zu beseitigen.
Nein, darum ging es ihm nicht und das tat er auch nicht. Die Beschleunigung ist in der ART die kovariante Ableitung der Vierergeschwindigkeit entlang der Weltlinie. Das ist keine bezugssystemabhängige Größe. |
Einstein schreibt in seinem Buch (Über die spezielle und die allgemeine Relativitätstheorie) selbst: ...Wir fühlen uns daher zunächst genötigt, entgegen dem Allgemeinen Relativitätsprinzip der ungleichförmigen Bewegung eine Art absolute physikalische Realität zuzusprechen. Im folgenden werden wir aber bald sehen, dass dieser Schluss nicht stichhaltig ist." Deine Ansicht, dass die Beschleunigung in der ART also auch eine absolute Beschleunigung ist teilt Einstein offensichtlich nicht. |
Gut, das will ich nicht mal ausschließen. Einsteins Verständnis seiner eigenen Theorie hat sich sicher im Laufe der Zeit etwas gewandelt. Also nehme ich meine Aussage darüber, worum es Einstein ging, zurück. Allerdings hat sich auch das allgemeine Verständnis seiner Theorie, selbst Jahrzehnte nach Einsteins Tod, noch weiterentwickelt. Dasselbe gilt übrigens für Newtons Theorie. Es bringt also generell nicht viel bei der Diskussion beider Theorien mit Einstein- oder Newtonzitaten zu argumentieren. Ich muß nämlich nicht bestreiten, daß sie etwas behauptet haben, sondern nur, daß sie damit recht hatten.
Was ich also nicht zurücknehme ist die Behauptung, daß die Beschleunigung eines Teilchens, sowohl in der ART als auch in der Newtonschen Mechanik, eine absolute, bezugssystemunabhängige Größe ist. Wenn Einstein anderer Ansicht war, dann lag er falsch. Formal ist das völlig unbestreitbar. Es handelt sich wie gesagt bei der Beschleunigung um die kovariante Ableitung
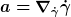
des Tangentialvektors 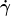 entlang der Weltlinie entlang der Weltlinie  . Daran, daß dies bezugssystemunabhängig ist, gibt es überhaupt nichts zu deuten. . Daran, daß dies bezugssystemunabhängig ist, gibt es überhaupt nichts zu deuten.
Ich würde gern versuchen dir anschaulich zu erklären warum das Kriterium der Geradlinig-Gleichförmigkeit keinen Bezug zum absoluten Raum benötigt. Ich weiß aber nicht ob das viel bringt, denn du scheinst mir einfach nicht glauben zu wollen. Vielleicht versuche ich später noch einen Erklärungsversuch mit Raumzeitdiagrammen, statt Worten und Formeln. Du kannst es aber auch gern mit etwas Literatur probieren. Zur Struktur der Newtonschen Raumzeit, inklusive Bedeutung des absoluten Raumes und der Absolutheit der Beschleunigung kann ich folgende Bücher empfehlen
Arnold, Mathematical Methods of Classical Mechanics
Misner, Thorne, Wheeler, Gravitation (insbesondere Kapitel 12 zur Newtonschen Theorie)
Dirschmid, Tensoren und Felder.
Zuletzt bearbeitet von index_razor am 22. Dez 2018 19:32, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Dez 2018 18:27 Titel: index_razor Verfasst am: 22. Dez 2018 18:27 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | | Einstein schreibt in seinem Buch (Über die spezielle und die allgemeine Relativitätstheorie) selbst: ...Wir fühlen uns daher zunächst genötigt, entgegen dem Allgemeinen Relativitätsprinzip der ungleichförmigen Bewegung eine Art absolute physikalische Realität zuzusprechen. Im folgenden werden wir aber bald sehen, dass dieser Schluss nicht stichhaltig ist." Deine Ansicht, dass die Beschleunigung in der ART also auch eine absolute Beschleunigung ist teilt Einstein offensichtlich nicht. |
Ich denke, das kann ich inzwischen aufklären. Einstein versteht unter Beschleunigung die zweite Ableitung der Ortskoordinaten nach der Zeit, also

Das ist ersichtlich aus einer Formel auf Seite 43:
} = \frac{\text{(schwere Masse)}}{\text{(träge Masse)}}\cdot\begin{pmatrix}\text{Intensität des}\\ \text{Schwerefeldes}\end{pmatrix} )
Das erklärt seine Aussage und sie ist nicht falsch. Sie widerspricht allerdings auch nicht meiner, denn ich habe ja bereits darauf hingewiesen, daß diese Größe vom Bezugssystem abhängig ist. Ich zähle allerdings, wegen des Äquivalenzprinzips, die Intensität des Schwerefeldes mit zur Beschleunigung, wie es heute (zumindest in der ART) allgemein üblich ist. (Und das ergibt eine bezugssystemunabhängige Größe.)
Das bedeutet, im Hinblick auf meine früheren Aussagen, daß das Schwerefeld Teil der Zusammenhangskoeffizienten  und damit Bestandteil der Geometrie der Raumzeit ist. Das ist genau die Konsequenz aus dem Äquivalenzprinzip und der Gleichsetzung von träger und schwerer Masse in der Formel auf S. 43, für die die ART berühmt ist. und damit Bestandteil der Geometrie der Raumzeit ist. Das ist genau die Konsequenz aus dem Äquivalenzprinzip und der Gleichsetzung von träger und schwerer Masse in der Formel auf S. 43, für die die ART berühmt ist.
|
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 300
|
 Corbi Verfasst am: 22. Dez 2018 19:41 Titel: Corbi Verfasst am: 22. Dez 2018 19:41 Titel: |
 |
|
| Zitat: | | Meines Wissens wollte Newton gerade für die Absolutheit der Beschleunigung argumentieren, nicht für die Existenz eines absoluten Bezugssystems. Aber genau weiß ich es zugegebenermaßen nicht. Es spielt aber m.E. keine Rolle, denn in der Newtonschen Mechanik gilt das Galileische Relativitätsprinzip. Ein absolutes Bezugssystem würde diesem Prinzip ja nun drastisch widersprechen. |
Es widerspricht dem Galileischen Relativitätsprinzip überhaupt nicht. Die gleichförmige Bewegung in diesem absoluten Bezugssystem ist nicht von der Ruhe zu unterscheiden.
| Zitat: | | Aber da du es zitiert hast, kannst du mir sicher erklären was genau mit "allen absoluten Bewegungen" gemeint ist |
Mit "allen absoluten Bewegungen" sind eben die ungleichförmigen Bewegungen gemeint. Und die absolute Ruhe in diesem Bezugssystem wäre in der Tat nicht feststellbar. Es kann nur festgestellt werden ob es sich gleichförmig in diesem Bezugsystem bewegt oder ob es sich ungleichförmig bewegt.
| Zitat: | | Ich würde gern versuchen dir anschaulich zu erklären warum das Kriterium der Geradlinig-Gleichförmigkeit keinen Bezug zum absoluten Raum benötigt. Ich weiß aber nicht ob das viel bringt, denn du scheinst mir einfach nicht glauben zu wollen. Vielleicht versuche ich später noch einen Erklärungsversuch mit Raumzeitdiagrammen, statt Worten und Formeln. Du kannst es aber auch gern mit etwas Literatur probieren. Zur Struktur der Newtonschen Raumzeit, inklusive Bedeutung des absoluten Raumes und der Absolutheit der Beschleunigung kann ich folgende Bücher empfehlen |
Ich würde es dir gerne glauben, es erscheint mir nur einfach absolut unplausibel. Über einen Erklärungsversuch anhand von Raumzeitdiagrammen würde ich mich freuen. Ansonsten habe ich auch nicht das Gefühl das eine Weitere Diskussion förderlich ist. Auf jeden Fall Vielen Dank für deine ausführlichen Antworten!
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Dez 2018 19:58 Titel: index_razor Verfasst am: 22. Dez 2018 19:58 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | | Zitat: | | Meines Wissens wollte Newton gerade für die Absolutheit der Beschleunigung argumentieren, nicht für die Existenz eines absoluten Bezugssystems. Aber genau weiß ich es zugegebenermaßen nicht. Es spielt aber m.E. keine Rolle, denn in der Newtonschen Mechanik gilt das Galileische Relativitätsprinzip. Ein absolutes Bezugssystem würde diesem Prinzip ja nun drastisch widersprechen. |
Es widerspricht dem Galileischen Relativitätsprinzip überhaupt nicht. Die gleichförmige Bewegung in diesem absoluten Bezugssystem ist nicht von der Ruhe zu unterscheiden.
|
Wozu soll es dann gut sein? Um absolute Beschleunigung mittels der Bedingung

festzusetellen, benötige ich nicht ein absolutes Bezugssystem, sondern lediglich eine Klasse von ausgezeichneten Bezugssystemen, die  invariant lassen. Diese werden normalerweise "Inertialsysteme" genannt. Keines davon verdient, wegen des Relativitätprinzips, die Bezeichnung "absolutes Bezugssytem". invariant lassen. Diese werden normalerweise "Inertialsysteme" genannt. Keines davon verdient, wegen des Relativitätprinzips, die Bezeichnung "absolutes Bezugssytem".
Allerdings kann ich dann auch die Beschleunigung in jedem beliebigen System feststellen, wenn ich weiß wie sich die Zusammenhangskoeffizienten  transformieren. (Deren Transformationsgesetz kannst du ebenfalls bei Wikipedia, aber auch in den Büchern, die ich dir genannt habe, nachlesen.) Und in allen Bezugssystemen ergibt sich damit dasselbe Resultat: entweder ist der Körper in allen Systemen unbeschleunigt oder in keinem. transformieren. (Deren Transformationsgesetz kannst du ebenfalls bei Wikipedia, aber auch in den Büchern, die ich dir genannt habe, nachlesen.) Und in allen Bezugssystemen ergibt sich damit dasselbe Resultat: entweder ist der Körper in allen Systemen unbeschleunigt oder in keinem.
Versuche einfach erstmal das nachzuvollziehen, bevor du wieder bestreitest, daß es stimmt.
| Zitat: |
| Zitat: | | Ich würde gern versuchen dir anschaulich zu erklären warum das Kriterium der Geradlinig-Gleichförmigkeit keinen Bezug zum absoluten Raum benötigt. Ich weiß aber nicht ob das viel bringt, denn du scheinst mir einfach nicht glauben zu wollen. Vielleicht versuche ich später noch einen Erklärungsversuch mit Raumzeitdiagrammen, statt Worten und Formeln. Du kannst es aber auch gern mit etwas Literatur probieren. Zur Struktur der Newtonschen Raumzeit, inklusive Bedeutung des absoluten Raumes und der Absolutheit der Beschleunigung kann ich folgende Bücher empfehlen |
Ich würde es dir gerne glauben, es erscheint mir nur einfach absolut unplausibel.
|
Was genau erscheint dir unplausibel? Ich erwarte ja nicht, daß du mir unkritisch glaubst was ich sage. Aber ich habe den Eindruck du versuchst nicht mal zu verstehen was ich meine, bevor du widersprichst. Du akzeptierst offenbar nicht mal, daß "Raum" und "Koordinatensystem" völlig verschiedene Konzepte sind. Das ist keine günstige Voraussetzung.
Versuchen wir es mal so: Erscheint es dir plausibel, daß du eine Gerade im Raum als solche erkennen kannst, ohne irgendein absolutes Koordinatensystem zu wählen?
Wenn nicht, wie wählst du es? An welchen Eigenschaften erkennst du es? Müssen seine Achsen Geraden sein? Dann befindest du dich in einem Zirkelschluß.
Wenn doch, warum erscheint es dir unplausibel, daß du eine Gerade in der Raumzeit ebenso ohne Bezug auf ein absolutes Bezugssystem erkennen kannst?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 23. Dez 2018 12:05 Titel: TomS Verfasst am: 23. Dez 2018 12:05 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | | Die gleichförmige Bewegung in diesem absoluten Bezugssystem ist nicht von der Ruhe zu unterscheiden. |
| Zitat: | | Und die absolute Ruhe in diesem Bezugssystem wäre in der Tat nicht feststellbar. |
Evtl. hilft es, anstelle der Bezugssysteme gedachte Beobachter einzuführen; das funktioniert sowohl bei Newton als auch bei Einstein, in der SRT sowie in der ART.
Ein gedachter Beobachter trägt dabei sein lokales Koordinatensystem mit sich herum. Das Vergehen seiner Koordinatenzeit misst er auf seiner Uhr, d.h. seine lokale Koordinatenzeit entspricht seiner Eigenzeit (was in der SRT wichtig wird). Die räumlichen Koordinatenachsen kann er beliebig wählen.
Infinitesimal benachbarte Beobachter weisen infinitesimal benachbarte Geschwindigkeiten auf, und ihre räumlichen Koordinatenachsen sind infinitesimal gegeneinander rotiert, d.h. das Feld der Beobachter weist keine Unstetigkeiten auf. Du kannst dir den Raum dicht gefüllt mit gedachten, punktförmigen, masselosen Beobachtern vorstellen, d.h. das Feld der Beobachter ist dicht im Raum.
Man kann die Newtonsche Mechanik sowie SRT und ART mittels derartiger Beobachterfelder formulieren. Physikalische Größen entsprechen dann immer messbare Größen bzgl. des Beobachterfeldes.
Frage: welches Beobachterfeld möchtest du nun als absolut auszeichnen?
Dann noch zwei Anmerkungen:
1) Bei der Entsprechung der Galilei-Invarianz in der SRT handelt es sich nicht um die Lorentz- sondern um die Poincaré-Invarianz.
2) Sowohl Lorentz- als auch Poincaré-Invarianz spielen in der ART eine völlig andere Rolle als in der SRT. Aufgrund der gekrümmten Raumzeit ist bereits die Lorentz-Invarianz keine globale Symmetrie mehr; die Raumzeit sowie Observablen sind nicht global Lorentz-kovariant bzw. -invariant. Stattdessen spielt die Lorentz-Invarianz die Rolle einer lokalen Eichsymmetrie; dies entspricht den lokalen SO(3,1) Rotationen der oben eingeführten Koordinatensysteme der gedachten Beobachter.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 23. Dez 2018 23:34 Titel: VeryApe Verfasst am: 23. Dez 2018 23:34 Titel: |
 |
|
| indexrazor hat Folgendes geschrieben: |
Wozu soll es dann gut sein? Um absolute Beschleunigung mittels der Bedingung

festzusetellen, benötige ich nicht ein absolutes Bezugssystem, sondern lediglich eine Klasse von ausgezeichneten Bezugssystemen, die  invariant lassen. Diese werden normalerweise "Inertialsysteme" genannt. Keines davon verdient, wegen des Relativitätprinzips, die Bezeichnung "absolutes Bezugssytem". invariant lassen. Diese werden normalerweise "Inertialsysteme" genannt. Keines davon verdient, wegen des Relativitätprinzips, die Bezeichnung "absolutes Bezugssytem".
|
Sehe ich auch so, jedoch sind diese nach Newton gleichförmig gerade im absoluten Raum bewegt oder in Ruhe.
Beschleunigungen gegenüber den absoluten Raum sind absolute Beschleunigungen von mir aus tatsächliche Beschleunigungen und erfordern Wechselwirkungskräfte während Beschleunigungen in Nichtinertialsystem Scheinbeschleunigungen sind.
In allen Bezugsystemen die auf den absoluten Raum beschleunigt sind, treten Trägheitskräfte auf.
Der absolute Raum ist m.E. ein physikalischer Raum der unabhängig von den Akteuren exisitiert und auch nicht durch die Akteure verändert werden kann. 1 Meter bleibt 1 Meter.
Wie soll Newton nun erklären ohne den absoluten Raum einzuführen, warum das eine Scheinbeschleunigungen sind und das andere absolute, warum über alle Intertialsystem hinweg auch noch die Beschleunigunswerte exakt gleich sind und warum das eine reale Wechselwirkungskräfte erfordert und das andere nur Scheinkräfte oder ein Zusammenspiel daraus.
Ich denke das meinte Corbi,
So wie ich Machs Einwand gegen Newton verstande habe.
Nehmen wir ein leeres Universum die Erde und den Eimer mit Wasser.
Nach Newton bildet das Wasser einfachen einen parabolischen Wasserstand , weil das Wasser einfach gegenüber den absoluten Raum beschleunigt wird, und das erfordert nach Newton Kräfte auf das Wasser.
Nach Mach müsste aber ausschließlich die Beschleunigung bzw Relativebewegung des Wassers zu den anderen Massen im Universum eine Rolle spielen für den Ausgang des Experiments und nicht zu irgendeinen ansonsten leeren Raum. Der leere absolute Raum das Nichts kann doch nicht den Ausgang des Experiments bestimmen.
wenn das Universum sonst leer wäre, würde das Wasser wahrscheinlich weiter gerade im Eimer liegen bleiben, obwohl es rotiert.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 24. Dez 2018 12:55 Titel: TomS Verfasst am: 24. Dez 2018 12:55 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | Nach Mach müsste aber ausschließlich die Beschleunigung bzw Relativebewegung des Wassers zu den anderen Massen im Universum eine Rolle spielen für den Ausgang des Experiments und nicht zu irgendeinen ansonsten leeren Raum. Der leere absolute Raum das Nichts kann doch nicht den Ausgang des Experiments bestimmen.
Wenn das Universum sonst leer wäre, würde das Wasser wahrscheinlich weiter gerade im Eimer liegen bleiben, obwohl es rotiert. |
Nach Mach wäre das so, nach Einstein jedoch sicher nicht.
In der ART dient die lokale Geometrie der Raumzeit als Referenzrahmen für die Definition und Wirkung von Trägheit. Trägheit ist zunächst ausschließlich gegeben als ein „Maß für den Widerstand gegen eine Abweichung“ der tatsächlichen Bewegung von der geodätischen Bewegung.
Insofern ist für eine gegebene Raumzeit die Klasse der geodätischen und damit kräftefreien Bewegungen physikalisch ausgezeichnet.
Ein Bezugsystem ist damit jedoch noch nicht ausgezeichnet. Die Geodätengleichung

für die Vierergeschwindigkeit u ist koordinatenfrei gegeben.
Wie nun diese lokale Geometrie der Raumzeit zustandekommt, ob durch ferne Massen verursacht oder nicht, ob gar eine vollständig leere Raumzeit vorliegt - d.h. Abwesenheit jeglicher Materie, Felder, Energie, ... - oder nicht, ist für die Trägheit irrelevant.
Das Machsche Prinzip war als Idee historisch für Einstein relevant, in der heutigen Formulierung der ART ist es bestenfalls irrelevant, m.E. sogar explizit nicht zutreffend.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 24. Dez 2018 16:56 Titel: index_razor Verfasst am: 24. Dez 2018 16:56 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | Beschleunigungen gegenüber den absoluten Raum sind absolute Beschleunigungen von mir aus tatsächliche Beschleunigungen und erfordern Wechselwirkungskräfte während Beschleunigungen in Nichtinertialsystem Scheinbeschleunigungen sind.
In allen Bezugsystemen die auf den absoluten Raum beschleunigt sind, treten Trägheitskräfte auf.
Der absolute Raum ist m.E. ein physikalischer Raum der unabhängig von den Akteuren exisitiert und auch nicht durch die Akteure verändert werden kann. 1 Meter bleibt 1 Meter.
Wie soll Newton nun erklären ohne den absoluten Raum einzuführen, warum das eine Scheinbeschleunigungen sind und das andere absolute, warum über alle Intertialsystem hinweg auch noch die Beschleunigunswerte exakt gleich sind und warum das eine reale Wechselwirkungskräfte erfordert und das andere nur Scheinkräfte oder ein Zusammenspiel daraus.
Ich denke das meinte Corbi,
|
Ich denke was er meint, ist ungefähr folgendes: Newtonsche Mechanik basiert auf einem absoluten Raum und einer absoluten Zeit, die unabhängig voneinander existieren. Der absolute Raum 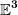 ist dreidimensional und euklidisch, die absolute Zeit ist dreidimensional und euklidisch, die absolute Zeit  ist eindimensional und affin (d.h. bis auf eine Skala und einen Nullpunkt eindeutig definiert). Die unabhängige Existenz von Raum und Zeit bedeutet, daß, sofern man überhaupt von einer Newtonschen Raumzeit sprechen will, diese die Struktur ist eindimensional und affin (d.h. bis auf eine Skala und einen Nullpunkt eindeutig definiert). Die unabhängige Existenz von Raum und Zeit bedeutet, daß, sofern man überhaupt von einer Newtonschen Raumzeit sprechen will, diese die Struktur  hat. hat.
Das ist durchaus ein mögliches Modell für eine Formulierung der Mechanik. Aber gerade im Kontext dieser Diskussion ist es wichtig zu verstehen, daß es streng genommen zu viel mathematische Struktur einführt, nämlich die Möglichkeit Ereignisse zu verschiedenen Zeiten ohne weiteren Bezug miteinander als "gleichortig" zu identifizieren. Das Problem ist folgendes: Innerhalb von  ist es kein Problem absolute Ruhe zu definieren. (Nicht zu messen, aber dazu komme ich gleich.) Ein beliebiger Körper folgt unter dem Einfluß irgendeiner Kraft einer Weltlinie ist es kein Problem absolute Ruhe zu definieren. (Nicht zu messen, aber dazu komme ich gleich.) Ein beliebiger Körper folgt unter dem Einfluß irgendeiner Kraft einer Weltlinie
))
durch die Raumzeit, wobei t eine affine Parametrisierung von  ist und ist und ) eine Kurve in eine Kurve in 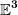 . Absolute Ruhe bedeutet nichts weiter, als daß sich der Körper zu jedem Zeitpunkt t am selben absoluten Ort in . Absolute Ruhe bedeutet nichts weiter, als daß sich der Körper zu jedem Zeitpunkt t am selben absoluten Ort in 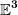 befindet, also befindet, also =\text{konst.}) ist. ist.
Ich denke das ist auch mehr oder weniger Hintergrund seiner Behauptung der absoute Raum stelle ein "absolutes Bezugssystem" dar, und innerhalb des Modells  ist das auch vollkommen natürlich. Aber notwendig ist das nicht. Und wenn man erkennt, daß "Bewegung relativ zum absoluten Raum" bereits in der Newtonschen Mechanik ein unnötiges Konzept ist, muß man sich nicht mehr fragen, wodurch es in der ART ersetzt wird. ist das auch vollkommen natürlich. Aber notwendig ist das nicht. Und wenn man erkennt, daß "Bewegung relativ zum absoluten Raum" bereits in der Newtonschen Mechanik ein unnötiges Konzept ist, muß man sich nicht mehr fragen, wodurch es in der ART ersetzt wird.
Die Basis für diese Erkenntnis legt er sich übrigens selbst: Er behauptet ja weiter, daß diese absolute Ruhe nicht "feststellbar" ist. Aber was heißt das genau? Feststellen, also messen, können wir in der Mechanik alle Phänomene, die mit der Bewegung träger Teilchen zu tun haben. Diese Bewegung wird durch Kräfte verursacht, und alle Informationen über diese Ursachen müssen wir eben aus der Teilchenbewegung erschließen. Jetzt wissen wir aber empirisch, daß alle Kraftgesetze galilei-invariant sind, d.h. jede Lösung der Newtonschen Bewegungsgleichungen geht unter Galileitransformation in eine andere Lösung über. Wir können also folgende Situationen nicht unterscheiden:
1) Wir beobachten die Bewegung eines Teilchens relativ zum absoluten Raum oder
2) Wir beobachten die Bewegung desselben Teilchens relativ zu einem System, welches sich wiederum relativ zum absoluten Raum mit konstanter Geschwindigkeit bewegt.
Oder anders formuliert: wir können niemals mit mechanischen Mitteln unterscheiden, ob ein Teilchen relativ zum absoluten Raum ruht oder geradlinig-gleichförmig bewegt ist. Beides ist einfach eine kräftefreie Bewegung.
Das Relativitätsprinzip ist hier aber lediglich ein empirisch aus der der Form der zulässigen Kraftgesetze abgeleitetes Resultat. Es steht im Konflikt mit der fundamentalen Struktur der Raumzeit  , welche eine unbeobachtbare Identifizierung von Raumpunkten zu verschiedenen Zeiten gestattet, und somit theoretische Behauptungen über absolute Geschwindigkeiten enthält, die prinzipiell nicht verifizierbar sind. , welche eine unbeobachtbare Identifizierung von Raumpunkten zu verschiedenen Zeiten gestattet, und somit theoretische Behauptungen über absolute Geschwindigkeiten enthält, die prinzipiell nicht verifizierbar sind.
Manchmal lassen wir in der Physik ähnliche ("metaphysische") Aussagen zu, wenn sie von theoretischem Wert sind. Zum Beispiel führen wir in die Elektrodynamik Freiheitsgrade ein, die nicht direkt beobachtbar sind, und zwar aus dem Grund, daß Eichfreiheit ein wichtiges theoretisches Konzept ist. Manchmal lehnen wir sie ab, wie zum Beispiel beim Äther. Die Frage ist also: ist die obige absolute Zerlegung  der Newtonschen Raumzeit eher wie die Eichpotentiale der Elektrodynamik oder wie der Äther? der Newtonschen Raumzeit eher wie die Eichpotentiale der Elektrodynamik oder wie der Äther?
Um es nicht unnötig in die Länge zu ziehen: Sie sind exakt wie der Äther, und jeden, den es interessiert wie man das Relativitätsprinzip von vornherein in die Struktur der Newtonschen Raumzeit einbaut, empfehle ich einen Blick in die Literatur, die ich weiter oben genannt habe.
Es bleibt die Frage: "Wie soll Newton nun erklären ohne den absoluten Raum einzuführen, warum das eine Scheinbeschleunigungen sind und das andere absolute, warum über alle Intertialsystem hinweg auch noch die Beschleunigunswerte exakt gleich sind und warum das eine reale Wechselwirkungskräfte erfordert und das andere nur Scheinkräfte oder ein Zusammenspiel daraus."
Je nach Ausgangspunkt sind hier mehrere Antworten möglich. Wir können z.B. das 1. Newtonsche Axiom zugrunde legen: Danach müssen wir einen Körper nur hinreichend von äußeren Kräften, Wechselwirkungen mit anderen Körpern, etc. isolieren und wissen (mit axiomatischer Gewissheit sozusagen), daß die Bewegung, die er nun noch ausführt, geradlinig-gleichförmig verläuft. Und zwar ist dies unabhängig davon von welchem Bezugssystem aus wie diese Bewegung beobachten. Stellen wir z.B. fest, daß  , wissen wir, daß es sich nicht um ein Inertialsystem handelt. Die komische Form der Bahnkurve in diesem System ändert nichts an der Geradlinig-gleichförmigkeit der Bewegung. Diese wird nur durch die Bewegung unserer beliebig gewählten Achsen verschleiert. Die Logik können wir natürlich auch umdrehen: Wenn wir aus irgendwelchen Gründen wissen, daß wir in einem Inertialsystem ruhen, können wir die Kräftefreiheit des Körpers durch die Bedingung , wissen wir, daß es sich nicht um ein Inertialsystem handelt. Die komische Form der Bahnkurve in diesem System ändert nichts an der Geradlinig-gleichförmigkeit der Bewegung. Diese wird nur durch die Bewegung unserer beliebig gewählten Achsen verschleiert. Die Logik können wir natürlich auch umdrehen: Wenn wir aus irgendwelchen Gründen wissen, daß wir in einem Inertialsystem ruhen, können wir die Kräftefreiheit des Körpers durch die Bedingung 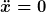 feststellen, aber nur dann. feststellen, aber nur dann.
Die Situation ist auf dieser Ebene nicht wesentlich verschieden von der ART: Man benötige nur eine Struktur, mit deren Hilfe man Geradheit und Gekrümmtheit von Kurven unterscheiden kann. Physikalisch liefert diese Struktur das 1. Axiom, mathematisch bedeutet es nur, daß die Raumzeit, sowohl die Newtonsche als auch die Einsteinsche, eine Vorschrift zur Paralleverschiebung von Vektoren beinhaltet. Was man in beiden Fällen nicht benötigt, ist ein absolutes Bezugssystem.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 25. Dez 2018 10:06 Titel: TomS Verfasst am: 25. Dez 2018 10:06 Titel: |
 |
|
Ganz allgemein sollte man die physikalische Struktur immer modulo der Symmetriegruppe definieren.
Im Falle der Newtonschen Mechanik wäre dies die von dir eingeführte Struktur modulo Galilei-Gruppe

Im Falle der speziellen Relativitätstheorie wäre dies der Mikowskiraum modulo Poincarégruppe

Im Falle der allgemeinen Relativitätstheorie wäre dies eine Riemannsche Mannigfaltigkeit modulo deren Diffeomorphismen
 / \text{Diff})
Ich denke, dieses Muster sagt in allen drei Fällen das selbe: die zusätzliche Struktur von Koordinaten- oder Bezugssystemen ist insofern unphysikalisch, als nichts davon physikalisch ausgezeichnet ist; es handelt sich um rechentechnische Hilfsmittel.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. Dez 2018 17:51 Titel: index_razor Verfasst am: 25. Dez 2018 17:51 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Ganz allgemein sollte man die physikalische Struktur immer modulo der Symmetriegruppe definieren.
Im Falle der Newtonschen Mechanik wäre dies die von dir eingeführte Struktur modulo Galilei-Gruppe

Im Falle der speziellen Relativitätstheorie wäre dies der Mikowskiraum modulo Poincarégruppe

|
Das klingt als sprächest du davon, die Orbits der entsprechenden Gruppe auf der Raumzeit als "physikalische Struktur" zu definieren. Das ist zumindest die Standardbedeutung von " ", wenn man Gruppenwirkungen ", wenn man Gruppenwirkungen  betrachtet. Galilei- und Poincare-Gruppe besitzen aber jeweils nur einen einzigen Orbit, nämlich die gesamte Raumzeit (leicht einzusehen, wenn man die Raumzeittranslationen betrachtet). Deswegen verstehe ich nicht, was genau du hier vorschlägst. betrachtet. Galilei- und Poincare-Gruppe besitzen aber jeweils nur einen einzigen Orbit, nämlich die gesamte Raumzeit (leicht einzusehen, wenn man die Raumzeittranslationen betrachtet). Deswegen verstehe ich nicht, was genau du hier vorschlägst.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 25. Dez 2018 20:56 Titel: VeryApe Verfasst am: 25. Dez 2018 20:56 Titel: |
 |
|
| indexrazor hat Folgendes geschrieben: |
nach Ausgangspunkt sind hier mehrere Antworten möglich. Wir können z.B. das 1. Newtonsche Axiom zugrunde legen: Danach müssen wir einen Körper nur hinreichend von äußeren Kräften, Wechselwirkungen mit anderen Körpern, etc. isolieren und wissen (mit axiomatischer Gewissheit sozusagen), daß die Bewegung, die er nun noch ausführt, geradlinig-gleichförmig verläuft. Und zwar ist dies unabhängig davon von welchem Bezugssystem aus wie diese Bewegung beobachten. Stellen wir z.B. fest, daß , wissen wir, daß es sich nicht um ein Inertialsystem handelt. Die komische Form der Bahnkurve in diesem System ändert nichts an der Geradlinig-gleichförmigkeit der Bewegung. Diese wird nur durch die Bewegung unserer beliebig gewählten Achsen verschleiert. Die Logik können wir natürlich auch umdrehen: Wenn wir aus irgendwelchen Gründen wissen, daß wir in einem Inertialsystem ruhen, können wir die Kräftefreiheit des Körpers durch die Bedingung feststellen, aber nur dann.
|
also wir gehen von der Basis aus wir messen, und wenn wir nichts feststellen, betiteln wir den Körper als kräftefrei.
Wenn wir jetzt feststellen das der Körper beschleunigt ist auf unser Koordinatensystem -> kein Inertialsystem.
Jetzt stell ich mir vor ich bin Newton steh am Boden und merke da drückt irgendetwas auf mich, das kann nicht kräftefrei sein.
Wenn ich mich fallen lassen würde, spüre ich nur den Luftwiderstand, wenn wir den aber beiseite lassen, müsste der Körper fast kräftefrei sein also ->
dieser Körper würde sich dann geradlinig gleichförmig bewegen.
Auf ein auf der Erde ruhendes Koordinatensystem wäre er aber beschleunigt, also Erde=Nicht Inertialsystem.
Nehme ich mir nun Koordinaten mit und lasse mich aus 1 Meter freifallen dann ist mein als geradlinig gleichförmiger indentifizierter Körper nicht beschleunigt, also sind die Koordinaten jetzt in einen Inertialsystem.
Plötzlich beschleunigt aber die 1 Meter entfernte gesamte Erde ohne Wechselwirkung auf mich zu .
Ein auf der gegenüberliegenden Seite ebenfalls frei fallender Beobachter der auch als kräftefrei indentifziert wurde beschleunigt auch auf mich zu.
Wie komme ich jetzt mit einem euklidischen Raum und einer absoluten Zeit weiter. was soll dann  für eine Bedeutung haben. für eine Bedeutung haben.
Da fliegen doch andere kräftefreie Körper irgendwie beschleunigt durcheinander.
An der Stelle steige ich immer aus, da kapiere ich nicht wies weiter geht.
Als Newton verwerfe ich dann den euklidischen Raum und die kartesischen Koordinaten oder was ist die Antwort drauf
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. Dez 2018 23:10 Titel: index_razor Verfasst am: 25. Dez 2018 23:10 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
Nehme ich mir nun Koordinaten mit und lasse mich aus 1 Meter freifallen dann ist mein als geradlinig gleichförmiger indentifizierter Körper nicht beschleunigt, also sind die Koordinaten jetzt in einen Inertialsystem.
Plötzlich beschleunigt aber die 1 Meter entfernte gesamte Erde ohne Wechselwirkung auf mich zu .
Ein auf der gegenüberliegenden Seite ebenfalls frei fallender Beobachter der auch als kräftefrei indentifziert wurde beschleunigt auch auf mich zu.
|
Das liegt alles nur daran, daß nun Gravitation im Spiel ist. In diesem Fall mußt du "kräftefrei" durch "frei fallend" ersetzen und statt 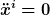 gilt gilt

Das bedeutet genau, daß das Ruhesystem eines frei fallenden Bezugskörpers nun im allgemeinen eben kein globales Inertialsystem mehr definiert, sondern nur noch ein lokales. Ein lokales Inertialsystem ist die bestmögliche Annäherung an ein globales Inertialsystem und wird definiert durch die Bedingung

am Ort des Bezugskörpers. Diese Bedingung kann aber nicht überall im Raum gelten, da im allgemeinen

(Gravitationskraft ändert sich von Ort zu Ort = Gezeiteneffekt.)
| Zitat: |
Wie komme ich jetzt mit einem euklidischen Raum und einer absoluten Zeit weiter. was soll dann  für eine Bedeutung haben. für eine Bedeutung haben.
|
Dies ist die Bewegungsgleichung eines frei fallenden Teilchens innerhalb eines lokalen Inertialsystems in der Nähe des "Ursprungs", d.h. dem Punkt, an dem die Bedingung  realisiert wurde. realisiert wurde.
| Zitat: |
Da fliegen doch andere kräftefreie Körper irgendwie beschleunigt durcheinander.
An der Stelle steige ich immer aus, da kapiere ich nicht wies weiter geht.
Als Newton verwerfe ich dann den euklidischen Raum und die kartesischen Koordinaten oder was ist die Antwort drauf |
Du hast zwei Möglichkeiten:
1) Du identifizierst "kräftefrei" = "frei fallend". Das legt die Bahnen, die der Bewegungsgleichung

gehorchen als Trägheitsbewegungen und damit (nach dem 1. Axiom) als geradlinig-gleichförmig (oder wenn dir das besser gefällt: geodätisch) fest. Das ist möglich, weil, wegen des Äquivalenzprinzips, diese Bahnen nur von den Anfangsbedingungen, aber nicht von den Eigenschaften der Testteilchen abhängen. Nun fliegen plötzlich kräftefreie Körper nicht mehr beschleunigt durcheinander, sondern geradlinig-gleichförmig, also unbeschleunigt. Die Geodätengleichung

impliziert zusammen mit  nun, daß die Raumzeit gekrümmt ist, wobei nun, daß die Raumzeit gekrümmt ist, wobei

Du mußt aber weder den euklidischen Raum, noch kartesische Koordinaten aufgeben. Nur die Flachheit der Raumzeit wird aufgegeben. (Nicht des Raumes; der bleibt wie gesagt flach und euklidisch.)
2) Du definierst irgendein lokales Inertialsystem willkürlich als globales Inertialsystem zusammen mit allen Systemen, die aus diesem durch Galilei-Transformationen hervorgehen. Das Problem: eine natürliche Wahl für ein globales Inertialsystem bietet sich normalerweise nicht an. Verschiedene Festlegungen für dieses globale Inertialsystem führen zu verschiedenen "Gravitationskräften" im selben Ereignis, die allerdings auf Grund des Äquivalenzprinzips physikalisch nicht unterscheidbar sind. (Dies ist analog zu dem Problem, daß die globale Zerlegung der Raumzeit  zu Aussagen über absolute Ruhe führen, die wegen des Relativitätsprinzips nicht von geradlinig-gleichförmiger Bewegung unterscheidbar ist.) Mit anderen Worten: die allgemeine Kovarianz der Theorie ist hin. zu Aussagen über absolute Ruhe führen, die wegen des Relativitätsprinzips nicht von geradlinig-gleichförmiger Bewegung unterscheidbar ist.) Mit anderen Worten: die allgemeine Kovarianz der Theorie ist hin.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 26. Dez 2018 02:11 Titel: TomS Verfasst am: 26. Dez 2018 02:11 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Das klingt als sprächest du davon, die Orbits der entsprechenden Gruppe auf der Raumzeit als "physikalische Struktur" zu definieren. Das ist zumindest die Standardbedeutung von " ", wenn man Gruppenwirkungen ", wenn man Gruppenwirkungen  betrachtet. Galilei- und Poincare-Gruppe besitzen aber jeweils nur einen einzigen Orbit, nämlich die gesamte Raumzeit (leicht einzusehen, wenn man die Raumzeittranslationen betrachtet). Deswegen verstehe ich nicht, was genau du hier vorschlägst. betrachtet. Galilei- und Poincare-Gruppe besitzen aber jeweils nur einen einzigen Orbit, nämlich die gesamte Raumzeit (leicht einzusehen, wenn man die Raumzeittranslationen betrachtet). Deswegen verstehe ich nicht, was genau du hier vorschlägst. |
Die links vom / stehenden Objekte tragen je nach Definition noch eine Struktur, z.B. Koordinatensysteme. Physikalisch relevant ist jedoch nur die Struktur modulo der Symmetriegruppe dieser Struktur.
Bsp. ART: Eine Riemannsche Mannigfaltigkeit (M,g) ist gegeben durch eine n-dim. Mannigfaltigkeit M sowie eine Metrik g auf M. Physikalisch relevant ist jedoch nur eine Raumzeit [M] als Äquivalenzklasse aller Riemannschen Mannigfaltigkeiten und Metriken bzgl. der Diffeomorphismen. Das führt auf den Orbit, und da habe ich kurz als /~ mit ~ für Gal, Poinc und Diff geschrieben. Der Begriff der Geodäte erscheint dann ganz natürlich und anschaulich als geradeste und zugleich kürzeste Kurve auf der Raumzeit, ohne dass dazu ein Koordinatensystem o.ä. notwendig wäre.
Wahrscheinlich hast du das mit deiner Notation bereits implizit so gemeint. Ich wollte das nur nochmal explizit hingeschrieben haben.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 26. Dez 2018 15:57 Titel: VeryApe Verfasst am: 26. Dez 2018 15:57 Titel: |
 |
|
| indexrazor hat Folgendes geschrieben: |
Das liegt alles nur daran, daß nun Gravitation im Spiel ist. In diesem Fall mußt du "kräftefrei" durch "frei fallend" ersetzen und statt 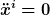 gilt gilt

Das bedeutet genau, daß das Ruhesystem eines frei fallenden Bezugskörpers nun im allgemeinen eben kein globales Inertialsystem mehr definiert, sondern nur noch ein lokales. Ein lokales Inertialsystem ist die bestmögliche Annäherung an ein globales Inertialsystem und wird definiert durch die Bedingung

am Ort des Bezugskörpers. Diese Bedingung kann aber nicht überall im Raum gelten, da im allgemeinen

(Gravitationskraft ändert sich von Ort zu Ort = Gezeiteneffekt.)
|
achso das ist das was du mir damals bei der Newton Cartan Theorie hingeschrieben hast.
Ich nehme den euklidischen Raum und die kartesischen Koordinaten und ziehe einen Teil der gesamten  Beschleunigung als Scheinbeschleunigung heraus, was eigentlich bei Newton nur im Nicht Inertialsystem vorkommt. Beschleunigung als Scheinbeschleunigung heraus, was eigentlich bei Newton nur im Nicht Inertialsystem vorkommt.
also





NIS... nicht Inertialsystem
IS... Inertialsystem
"a-koordinaten" wäre der Teil an Schein den man aus "a-NIS" herausrechnen (korrektur rechnen) müsste um auf die tatsächliche Beschleunigung im Inertialsystem zu schließen und jetzt kommt noch hinzu das man im Inertialsystem je nach Örtlichkeit nochmal Korrektur rechnen müsste und zwar noch den Teil der Gravitation als Schein herausrechnen müsste.
Das hätte aber schon ziemlich den Touch eines NIS, ob das Newton eingefallen wäre wenn er da noch tiefer nachgedacht hätte.
Kraftlose Körper fliegen dann da drinnen global auf krummen Bahnen und beschleunigt herum (=geradlinig gleichförmige Bewegung.....) und die Gravitation wäre keine Wechselwirkungskraft mehr.
das unter 2) habe ich noch nicht verstanden, da muß ich noch nachdenken.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Dez 2018 13:41 Titel: index_razor Verfasst am: 27. Dez 2018 13:41 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
achso das ist das was du mir damals bei der Newton Cartan Theorie hingeschrieben hast.
|
Die Newton-Cartan-Theorie ist nur eine allgemein kovariante Umformulierung der Newtonschen Mechanik. Bezogen auf ein beliebiges Koordinatensystem sind die Formeln dieselben.
| Zitat: |
Ich nehme den euklidischen Raum und die kartesischen Koordinaten und ziehe einen Teil der gesamten  Beschleunigung als Scheinbeschleunigung heraus, was eigentlich bei Newton nur im Nicht Inertialsystem vorkommt. Beschleunigung als Scheinbeschleunigung heraus, was eigentlich bei Newton nur im Nicht Inertialsystem vorkommt.
|
Die gesamte Beschleunigung ist eben nicht  , sondern , sondern

Das ist nicht einfach nur ein Buchhaltungstrick, bei dem willkürlich irgendwelche Größen auf die andere Seite der Gleichung geschrieben werden. Die Größe  hat absolute bezugsunabhängige Bedeutung, selbst unter Einbeziehung des Äquivalenzprinzips. Die Terme auf der rechten Seite sind jeweils für sich genommen bezugssystemabhängig. (Dies gilt auch für hat absolute bezugsunabhängige Bedeutung, selbst unter Einbeziehung des Äquivalenzprinzips. Die Terme auf der rechten Seite sind jeweils für sich genommen bezugssystemabhängig. (Dies gilt auch für  ). ).
Die Herleitung dieser Gl. ist nicht wesentlich anders als das, was man aus der Betrachtung beschleunigter Bezugssysteme in der nicht-kovarianten Formulierung der Mechanik kennt. Es kommt im wesentlichen nur eine Dimension hinzu (Formulierung der Newtonschen Mechanik auf einer vierdimensionalen "Newtonschen" Raumzeit, anstatt auf einem festen zeitunabhängigen 3-dimensionalen Raum).
Betrachte irgendeinen beliebig bewegten Bezugskörper der vier Achsen  zur Definition eines Koordinatensystems durch die Raumzeit transportiert. Ein Teilchen bewege sich auf Grund irgendwelcher Kräfte augenblicklich durch dasselbe Ereignis wie der Bezugskörper. Die Geschwindigkeit des Teilchens durch die Raumzeit ist zur Definition eines Koordinatensystems durch die Raumzeit transportiert. Ein Teilchen bewege sich auf Grund irgendwelcher Kräfte augenblicklich durch dasselbe Ereignis wie der Bezugskörper. Die Geschwindigkeit des Teilchens durch die Raumzeit ist

(Die 0-Komponente der Geschwindigkeit ist immer  wenn wir die Trajektorie mit der absoluten Zeit parametrisieren. Mit wenn wir die Trajektorie mit der absoluten Zeit parametrisieren. Mit  bezeichne ich die rein räumliche Komponente der Geschwindigkeit.) Beschleunigung ergibt sich aus der Änderung der Geschwindigkeit. Das heißt wir bilden die kovarianten Ableitung (=totale Zeitableitung entlang der Weltlinie des Teilchens) bezeichne ich die rein räumliche Komponente der Geschwindigkeit.) Beschleunigung ergibt sich aus der Änderung der Geschwindigkeit. Das heißt wir bilden die kovarianten Ableitung (=totale Zeitableitung entlang der Weltlinie des Teilchens)

Den ersten Term könnte man "Koordinatenbeschleunigung" nennen. Die folgenden beiden Terme entstehen durch die Änderung der Koordinatenachsen mit der Zeit. Wie in der nicht-kovarianten Formulierung beschreiben sie zum einen alle möglichen Artefakte die durch die willkürliche Bewegung der Achsen entstehen. Dazu zählen sowohl die "Trägheitskräfte" (pro Einheitsmasse), als auch exotischere Effekte, die z.B. durch eine zeitliche Änderung der relativen Neigung der Achsen enstehen können.
In der kovarianten Formulierung treten aber nun auch gravitative Effekte als natürliche Folge des Terms  hinzu. (Der in der elementaren 3+1-dimensionalen Formulierung nicht auftritt.) Die explizite Form des Terms in der Basis hinzu. (Der in der elementaren 3+1-dimensionalen Formulierung nicht auftritt.) Die explizite Form des Terms in der Basis  ist recht simpel ist recht simpel
e_i.)
Die Koeffizienten 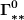 sind sämtlich null und die entsprechenden Terme kommen deshalb nicht vor. Die formale Begründung spare ich mir hier, aber sie hat direkt mit der Eigenschaft der absoluten Zeit zu tun, "an sich und vermöge ihrer Natur gleichförmig" zu verfließen. Der zweite Term sind sämtlich null und die entsprechenden Terme kommen deshalb nicht vor. Die formale Begründung spare ich mir hier, aber sie hat direkt mit der Eigenschaft der absoluten Zeit zu tun, "an sich und vermöge ihrer Natur gleichförmig" zu verfließen. Der zweite Term  , linear in der Geschwindigkeit, liefert einen Beitrag zur Corioliskraft. Aber der erste Term ist der Interessante und wird mit dem lokalen Gravitationsfeld identifiziert , linear in der Geschwindigkeit, liefert einen Beitrag zur Corioliskraft. Aber der erste Term ist der Interessante und wird mit dem lokalen Gravitationsfeld identifiziert
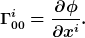
Vergleicht man die entsprechenden Terme relativ zu zwei verschieden beschleunigten Systemen so erhält man

d.h. die "Koordinatenbeschleunigung" des einen Bezugskörpers relativ zum anderen Bezugskörper, trägt an Ort und Stelle zum lokalen Gravitationsfeld bei. Das ist genau die Konsequenz aus dem Äquivalenzprinzip, die sich in Einsteins Gedankenexperiment im beschleunigten Fahrstuhl widerspiegelt.
Die verbleibenden Terme  vereinfachen sich erheblich (d.h. verschwinden zum größten Teil), wenn man geradlinige räumliche Achsen wählt, die zu jeder Zeit senkrecht aufeinander stehen (sich aber drehen können). Was übrig bleibt ist ein weiterer Term vereinfachen sich erheblich (d.h. verschwinden zum größten Teil), wenn man geradlinige räumliche Achsen wählt, die zu jeder Zeit senkrecht aufeinander stehen (sich aber drehen können). Was übrig bleibt ist ein weiterer Term  , der die zweite Hälfte der Corioliskraft darstellt. (Zentrifugalkräfte kommen nicht vor, da das Teilchen gerade durch den Ursprung fliegt.) Das heißt *) , der die zweite Hälfte der Corioliskraft darstellt. (Zentrifugalkräfte kommen nicht vor, da das Teilchen gerade durch den Ursprung fliegt.) Das heißt *)

("BS" steht für Bezugssystem und ist vermutlich mit deinem "a-Koordinaten" identisch.) Dies ist gleich der Kraft (pro Einheitsmasse) die von echten äußeren Feldern bzw. Wechselwirkungen verursacht wird, d.h.

Hier kommt überhaupt kein Bezug auf irgendein absolutes Koordinatensystem mehr vor, nicht mal auf ein Inertialsystem.
_______________
*) Der Faktor 2 vor der Corioliskraft entsteht hier durch Addition zweier gleicher Terme recht verschiedenen Ursprungs und ist offensichtlich auf die Symmetrie  der Zusammenhangskoeffizienten, und damit letztlich auf die Torsionsfreiheit des affinen Zusammenhangs zurückzuführen. der Zusammenhangskoeffizienten, und damit letztlich auf die Torsionsfreiheit des affinen Zusammenhangs zurückzuführen.
| Zitat: |
also





NIS... nicht Inertialsystem
IS... Inertialsystem
|
Das sieht irgendwie verkehrt aus. Warum sind hier auf verschiedene Systeme (IS und NIS) bezogene Größen in den Gleichungen vermischt?
Hat dir die (hoffentlich korrekte) Rechnung weiter oben noch etwas beim Verständnis geholfen?
| Zitat: |
"a-koordinaten" wäre der Teil an Schein den man aus "a-NIS" herausrechnen (korrektur rechnen) müsste um auf die tatsächliche Beschleunigung im Inertialsystem zu schließen und jetzt kommt noch hinzu das man im Inertialsystem je nach Örtlichkeit nochmal Korrektur rechnen müsste und zwar noch den Teil der Gravitation als Schein herausrechnen müsste.
|
Ich verstehe nicht was du mit "a-NIS" meinst. Schauen wir uns nochmal das Ergebnis oben in voller Allgemeinheit an:
_{\text{BS}} + \left(\Gamma^i_{00} + 2v^k\Gamma^i_{0k}+ v^k v^\ell\Gamma^i_{k\ell}\right)e_i.)
(Hier stehen auch noch die Terme  , die ich oben mit Hilfe der Wahl der räumlichen Achsen wegdiskutiert habe.) Die Moral von der ganzen Geschichte ist nun folgende: , die ich oben mit Hilfe der Wahl der räumlichen Achsen wegdiskutiert habe.) Die Moral von der ganzen Geschichte ist nun folgende:
1) Ich kann immer durch Wahl eines geeigneten (frei fallenden) Bezugskörpers und drehungsfreier Achsen alle  entlang der Weltlinie des Bezugskörpers (also in seinem "Ursprung" zu allen Zeiten) zum Verschwinden bringen, d.h. entlang der Weltlinie des Bezugskörpers (also in seinem "Ursprung" zu allen Zeiten) zum Verschwinden bringen, d.h.

Für alle Körper in der Nähe des Ursprungs gilt also
_\text{BS} = \ddot x^i e_i) . .
2) Einige der Koeffizienten  kann ich darüberhinaus auf Grund besonderer Eigenschaften der Raumzeit in jedem Punkt verschwinden lassen. Dazu gehören kann ich darüberhinaus auf Grund besonderer Eigenschaften der Raumzeit in jedem Punkt verschwinden lassen. Dazu gehören  , welches wegen der Existenz der absoluten Zeit verschwindet und , welches wegen der Existenz der absoluten Zeit verschwindet und  (für (für  ), dessen globales Verschwinden auf die Flachheit des absoluten Raumes zurückzuführen ist. ), dessen globales Verschwinden auf die Flachheit des absoluten Raumes zurückzuführen ist.
3) Einige andere Koeffizienten können aber nicht überall verschwinden, z.B.
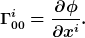
wegen der Inhomogenität echter Gravitationsfelder (also der Existenz des Gezeiteneffekts). Dies bedeutet, daß die Raumzeit gekrümmt ist.
| Zitat: |
Das hätte aber schon ziemlich den Touch eines NIS, ob das Newton eingefallen wäre wenn er da noch tiefer nachgedacht hätte.
Kraftlose Körper fliegen dann da drinnen global auf krummen Bahnen und beschleunigt herum (=geradlinig gleichförmige Bewegung.....) und die Gravitation wäre keine Wechselwirkungskraft mehr.
|
Nochmal, geradlinig-gleichförmig und unbeschleunigt ist dasselbe. Es bedeutet

Das bedeutet natürlich nicht unbedingt, daß
_\text{BS} = 0.)
Letzteres gilt nur, wenn zusätzlich
1) man ein lokales Inertialsystem gewählt hat (alle  verschwinden im Ursprung). verschwinden im Ursprung).
und
2) keine Gravitation vorhanden ist. (Alle  sind konstant, verschwinden also überall; das lokale Inertialsystem ist ein globales Inertialsystem). sind konstant, verschwinden also überall; das lokale Inertialsystem ist ein globales Inertialsystem).
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 27. Dez 2018 19:35 Titel: VeryApe Verfasst am: 27. Dez 2018 19:35 Titel: |
 |
|
| indexrazor hat Folgendes geschrieben: | | Hat dir die (hoffentlich korrekte) Rechnung weiter oben noch etwas beim Verständnis geholfen? |
Dazu müsste ich vorher nochmal nachfragen.
Du hast gesagt ich kann in mein freifallendes Bezugssystem kartesische Koordinaten mitnehmen und einen euklidischen Raum betrachten.
Mit diesen Koordinatensystem kann ich doch auch globale Situationen beschreiben, wie das, das ich aus einen Meter freifalle mit g und die Erde kommt mit in meinen Bezugssystem mit g entgegen und ein gegenüberliegender freifallender Beobachter kommt mir mit 2g entgegen.
Dieses System ist ein Inertialsystem (lokales) und die gesamte Beschleunigung die ich darin messe ist jetzt 
Ich kann doch auch in diesem System die Beschleunigung der Erde messen, die wäre
dann

und die des gegenüberliegenden Beobachters

stimmt das soweit.
Diese Beschleunigung ist aber nicht die Beschleunigung auf die Geodäte sondern dann müsste ich zu den  den Korrekturterm von dir hinzurechnen, der dann von der örtklichkeit in diesem Inertialsystem abhängt. den Korrekturterm von dir hinzurechnen, der dann von der örtklichkeit in diesem Inertialsystem abhängt.
Ich betrachte da zunächst keine 4D Raumzeit.
sondern einfach den Euklidischen 3D Raum plus die Zeit extra.
stimmt das mal?
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Dez 2018 20:17 Titel: index_razor Verfasst am: 27. Dez 2018 20:17 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
Dieses System ist ein Inertialsystem (lokales) und die gesamte Beschleunigung die ich darin messe ist jetzt 
|
Was ist die "gesamte" Beschleunigung? Das hast du nicht definiert. Meiner Definition nach ist es  , also die kovariante Ableitung der (Vierer-) Geschwindigkeit. Du scheinst den Term , also die kovariante Ableitung der (Vierer-) Geschwindigkeit. Du scheinst den Term  damit zu meinen, also nur den Anteil ohne Berücksichtigung der die Bewegung der Achsen. Ob sich die Achsen drehen oder nicht, ist aber ein Unterschied von fundamentaler Bedeutung. Deshalb erscheint mir die Bezeichnung "gesamte" Beschleunigung für damit zu meinen, also nur den Anteil ohne Berücksichtigung der die Bewegung der Achsen. Ob sich die Achsen drehen oder nicht, ist aber ein Unterschied von fundamentaler Bedeutung. Deshalb erscheint mir die Bezeichnung "gesamte" Beschleunigung für  irreführend. irreführend.
| Zitat: |
Ich kann doch auch in diesem System die Beschleunigung der Erde messen, die wäre
dann

und die des gegenüberliegenden Beobachters

stimmt das soweit.
Diese Beschleunigung ist aber nicht die Beschleunigung auf die Geodäte sondern dann müsste ich zu den  den Korrekturterm von dir hinzurechnen, der dann von der örtklichkeit in diesem Inertialsystem abhängt. den Korrekturterm von dir hinzurechnen, der dann von der örtklichkeit in diesem Inertialsystem abhängt.
|
Die Korrekturterme stehen doch schon da (zumindest einer davon), nämlich "g" bzw. "2g". Du hast ihn nur auf die andere Seite der Gleichung geschrieben. (Die Bewegungsgleichung, die ausdrückt, daß der Körper frei fällt.)
| Zitat: |
Ich betrachte da zunächst keine 4D Raumzeit.
sondern einfach den Euklidischen 3D Raum plus die Zeit extra.
stimmt das mal? |
Mein Argument ist aber gerade, daß man besser die Raumzeit betrachtet, um zu verstehen, daß man absolute Beschleunigung ohne absolutes Ruhesystem definieren kann. Solange du das nicht tun willst, gibt es nicht viel zu verstehen.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Dez 2018 20:22 Titel: index_razor Verfasst am: 27. Dez 2018 20:22 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
siehe Bild
Ich habe nur 2 Dimensionen verwendet um es leichter zu zeichnen
|
Ich habe eher ein fundamentales als ein geometrisches Problem bei der Interpretation. Deine Gleichungen scheinen Größen in Beziehung zu setzen, die sich auf unterschiedliche Systeme beziehen, deren Zusammenhang du nicht klar definiert hast. Das ist m.E. verwirrend und unnötig
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 27. Dez 2018 21:06 Titel: VeryApe Verfasst am: 27. Dez 2018 21:06 Titel: |
 |
|
| indexrazor hat Folgendes geschrieben: |
Was ist die "gesamte" Beschleunigung? Das hast du nicht definiert. Meiner Definition nach ist es , also die kovariante Ableitung der (Vierer-) Geschwindigkeit.
|
verstehe, nein das meinte ich nicht mit gesamter Beschleunigung.
| Zitat: | Du scheinst den Term  damit zu meinen, also nur den Anteil ohne Berücksichtigung der die Bewegung der Achsen. Ob sich die Achsen drehen oder nicht, ist aber ein Unterschied von fundamentaler Bedeutung. Deshalb erscheint mir die Bezeichnung "gesamte" Beschleunigung für damit zu meinen, also nur den Anteil ohne Berücksichtigung der die Bewegung der Achsen. Ob sich die Achsen drehen oder nicht, ist aber ein Unterschied von fundamentaler Bedeutung. Deshalb erscheint mir die Bezeichnung "gesamte" Beschleunigung für  irreführend. irreführend.
|
Ja, das glaube ich.
ich nehme einfach kartesische Koordinaten x,y,z in mein freifallendes Bezugssystem mit ( die Koordinate z zeigt in Fallrichtung) und meinte mit gesamte Beschleunigung die resultiernde Beschleunigung , die ich ermittle.
also für die Erde 
für den gegenüberliegenden Beobachter

gesamt habe ich deswegen geschrieben, weil sich diese Beschleunigung ja aus mehreren Einzelbeschleunigungen diverser Kräfte bilden kann wie in meinem Bild z.B. Beschleunigung von Fs1 und Beschleunigung von Fs2 ergibt die gesamte Beschleunigung der resuliternden, also hätte ich besser resultiernde Beschleunigung geschrieben.
Das ist bei dir 
und zu dieser Beschleunigung rechne ich jetzt noch bezugssystemabhängige Korrekturterme ab und komme dann auf eine Beschleunigung die du als gesamte Beschleunigung betitelst und die absolut ist, was mir rein von den Zahlenwerten auch schon klar ist, weil du ja in jeden bezugssystem örtlich spezifische Werte abziehst und kommst somit immer aufs gleiche.
Also für mich so wie wenn ich die Gravitationskraft als Scheinkraft herausrechne, dann bleibt die Beschleunigung der anderen Wechselwirkungskräfte über und die ist sowieso auch absolut.
Vorstellen kann ich mir das dann in der 4D Raumzeit so ungefähr wie hier.
4D bewegst sich das dann gerade gleichförmig.
https://www.youtube.com/watch?v=DdC0QN6f3G4
| Zitat: | Ich habe eher ein fundamentales als ein geometrisches Problem bei der Interpretation. Deine Gleichungen scheinen Größen in Beziehung zu setzen, die sich auf unterschiedliche Systeme beziehen, deren Zusammenhang du nicht klar definiert hast. Das ist m.E. verwirrend und unnötig
|
ja , ich hätte wohl besser von Anfang an eine Skizze angehängt.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Dez 2018 08:54 Titel: index_razor Verfasst am: 28. Dez 2018 08:54 Titel: |
 |
|
Hm, also so richtig ins Schwarze trifft deine Beschreibung immer noch nicht, finde ich.
| VeryApe hat Folgendes geschrieben: |
gesamt habe ich deswegen geschrieben, weil sich diese Beschleunigung ja aus mehreren Einzelbeschleunigungen diverser Kräfte bilden kann wie in meinem Bild z.B. Beschleunigung von Fs1 und Beschleunigung von Fs2 ergibt die gesamte Beschleunigung der resuliternden, also hätte ich besser resultiernde Beschleunigung geschrieben.
Das ist bei dir 
|
Es gilt  , wobei , wobei  die auf das Teilchen wirkende resultierende Kraft ist. Wäre es dann nicht besser man bezeichnet die auf das Teilchen wirkende resultierende Kraft ist. Wäre es dann nicht besser man bezeichnet 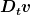 , und nicht , und nicht  , sowohl als "resultierende" als auch "gesamte" Beschleunigung? , sowohl als "resultierende" als auch "gesamte" Beschleunigung?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 28. Dez 2018 19:47 Titel: VeryApe Verfasst am: 28. Dez 2018 19:47 Titel: |
 |
|
| indexrazor hat Folgendes geschrieben: |
Es gilt  , wobei , wobei  die auf das Teilchen wirkende resultierende Kraft ist. Wäre es dann nicht besser man bezeichnet die auf das Teilchen wirkende resultierende Kraft ist. Wäre es dann nicht besser man bezeichnet 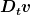 , und nicht , und nicht  , sowohl als "resultierende" als auch "gesamte" Beschleunigung? , sowohl als "resultierende" als auch "gesamte" Beschleunigung? |
Wenn ich mit meinem kartesischen Koordinatensystem x,y,z freifalle, und den gegenüberliegenden freifallenden Beobachter beschreibe, dann wäre demnach die resultiernde Beschleunigung null sowie die gesamte Beschleunigung null und die resultiernde Kraft null.
Und  wäre aber trotzdem -2g. wäre aber trotzdem -2g.
Wenn Geschwindigkeit die erste Ableitung von Koordinaten ist 
und Beschleunigung für die zweite Ableitung 
was für einen Ausdruck bleibt mir dann noch für die Beschleunigung -2g....
Ich dachte zuerst ich verwende den Ausdruck gesamte Beschleunigung die würde sich dann aus der resultiernden Beschleunigung ergeben die von denr resultierenden Kräften der echten Wechselwirkung kommt (ohne Gravitationswechselwirkungkräfte) plus ein Anteil an Schein der dann das null auf -2g bringt.
Wenn du alle zwei Begriffe schon besetzt, wie nennst du dann die Beschleunigung -2g , also einfach a_BS.
Denn die res Beschleunigung wäre dann null und die Gesamt Beschleunigung auch null
Wenn wir mal die Gravitation beiseite lassen und auf mein Bild kommen dann kann doch jedes Bezugssystem eine eigene resultierende Beschleunigung haben.
Im IS wäre die resulierende Beschleunigung a_is
Im NIS wäre die resultiernde Beschleunigung a_nis.
also völlig unterschiedliche resultiernde Beschleunigungen für den selben Sachverhalt, je nach Bezugssystem
Im Fall des NIS zähle ich auch die Trägheitskraft zu den Summe der resultiernden Kraft.
Im Falle Gravitation und lokales Inertialsystem zur Beschreibung globaler Situationen, entsteht ja ein Teil an Schein für mich den ich keine Scheinkraft zuordnen lann sondern einfach weil ich die Zeitachse nicht gekrümmt betrachte, ist das korrekt?
und somit habe ich nicht gewusst wie ich das nun Ausdrücken kann und Gesamtbeschleunigung hingeschrieben
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Dez 2018 13:11 Titel: index_razor Verfasst am: 29. Dez 2018 13:11 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | indexrazor hat Folgendes geschrieben: |
Es gilt  , wobei , wobei  die auf das Teilchen wirkende resultierende Kraft ist. Wäre es dann nicht besser man bezeichnet die auf das Teilchen wirkende resultierende Kraft ist. Wäre es dann nicht besser man bezeichnet 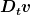 , und nicht , und nicht  , sowohl als "resultierende" als auch "gesamte" Beschleunigung? , sowohl als "resultierende" als auch "gesamte" Beschleunigung? |
Wenn ich mit meinem kartesischen Koordinatensystem x,y,z freifalle, und den gegenüberliegenden freifallenden Beobachter beschreibe, dann wäre demnach die resultiernde Beschleunigung null sowie die gesamte Beschleunigung null und die resultiernde Kraft null.
Und  wäre aber trotzdem -2g. wäre aber trotzdem -2g.
|
Soweit korrekt. Daraus folgt nur, daß  nicht die "Beschleunigung" ist, sondern lediglich die "Koordinatenbeschleunigung". Beide sind nur in globalen Inertialsystemen stets identisch. In Gravitationsfeldern existieren aber im allgemeinen keine globalen, sondern lediglich lokale Inertialsysteme. nicht die "Beschleunigung" ist, sondern lediglich die "Koordinatenbeschleunigung". Beide sind nur in globalen Inertialsystemen stets identisch. In Gravitationsfeldern existieren aber im allgemeinen keine globalen, sondern lediglich lokale Inertialsysteme.
| Zitat: |
Wenn Geschwindigkeit die erste Ableitung von Koordinaten ist 
und Beschleunigung für die zweite Ableitung 
[...]
|
Das ist wie gesagt nur die "Koordinatenbeschleunigung".
| Zitat: |
[...] was für einen Ausdruck bleibt mir dann noch für die Beschleunigung -2g....
|
Der Ausdruck  an dem entsprechenden Ereignis. Beantwortet das die Frage? an dem entsprechenden Ereignis. Beantwortet das die Frage?
| Zitat: |
Ich dachte zuerst ich verwende den Ausdruck gesamte Beschleunigung die würde sich dann aus der resultiernden Beschleunigung ergeben die von denr resultierenden Kräften der echten Wechselwirkung kommt (ohne Gravitationswechselwirkungkräfte) plus ein Anteil an Schein der dann das null auf -2g bringt.
Wenn du alle zwei Begriffe schon besetzt, wie nennst du dann die Beschleunigung -2g , also einfach a_BS.
Denn die res Beschleunigung wäre dann null und die Gesamt Beschleunigung auch null
|
Die kannst du nach wie vor "Gravitationsbeschleunigung" nennen. Die Differenz aus Gravitationsbeschleunigung und Koordinatenbeschleunigung ergibt dann die absolute Beschleunigung null

| Zitat: |
Wenn wir mal die Gravitation beiseite lassen und auf mein Bild kommen dann kann doch jedes Bezugssystem eine eigene resultierende Beschleunigung haben.
Im IS wäre die resulierende Beschleunigung a_is
Im NIS wäre die resultiernde Beschleunigung a_nis.
also völlig unterschiedliche resultiernde Beschleunigungen für den selben Sachverhalt, je nach Bezugssystem
|
Nein, die Beschleunigung als Vektor im Raum ist dieselbe, d.h. (links lokales Inertialsystem, rechts beliebiges Bezugssystem)
e_z = (\ddot x^i + 2v^k\Gamma^i_{0k} + g'^i)e'_i)
(Ich habe doch einen Gravitationsterm hinzugefügt, weil er den Sachverhalt m.E. nicht sonderlich kompliziert.) Lediglich die Komponenten ausgedrückt in der jeweiligen Basis unterscheiden sich. (Durch eine zeitabhängige Drehung, wenn beide Systeme orthogonale räumliche Achsen, also ein kartesisches Koordinatensystem, verwenden.) Solche Unterschiede existieren für alle euklidischen Vektoren.
| Zitat: |
Im Falle Gravitation und lokales Inertialsystem zur Beschreibung globaler Situationen, entsteht ja ein Teil an Schein für mich den ich keine Scheinkraft zuordnen lann sondern einfach weil ich die Zeitachse nicht gekrümmt betrachte, ist das korrekt?
|
Hm, mir gefällt die Formulierung "weil ich die Zeitachse nicht gekrümmt betrachte" nicht. Kannst du genauer erklären, wie das gemeint ist?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 30. Dez 2018 21:11 Titel: VeryApe Verfasst am: 30. Dez 2018 21:11 Titel: |
 |
|
| indexrazor hat Folgendes geschrieben: | Soweit korrekt. Daraus folgt nur, daß nicht die "Beschleunigung" ist, sondern lediglich die "Koordinatenbeschleunigung". Beide sind nur in globalen Inertialsystemen stets identisch. In Gravitationsfeldern existieren aber im allgemeinen keine globalen, sondern lediglich lokale Inertialsysteme.
|
Okay also dann Koordinatenbeschleunigung, die hatte ich die ganze Zeit gemeint, wenn ich Gesamtbeschleunigung vorher verwendet habe.
also verstanden
| Zitat: | | Beantwortet das die Frage? |
Koordinatenbeschleunigung beantwortet schon meine Frage, und den Anteil an Schein kann ich weiterhin Gravitationsbeschleunigung nennen.
| Zitat: |
Die kannst du nach wie vor "Gravitationsbeschleunigung" nennen. Die Differenz aus Gravitationsbeschleunigung und Koordinatenbeschleunigung ergibt dann die absolute Beschleunigung null
|
klar
| Zitat: |
Nein, die Beschleunigung als Vektor im Raum ist dieselbe, d.h. (links lokales Inertialsystem, rechts beliebiges Bezugssystem)
(Ich habe doch einen Gravitationsterm hinzugefügt, weil er den Sachverhalt m.E. nicht sonderlich kompliziert.) Lediglich die Komponenten ausgedrückt in der jeweiligen Basis unterscheiden sich. (Durch eine zeitabhängige Drehung, wenn beide Systeme orthogonale räumliche Achsen, also ein kartesisches Koordinatensystem, verwenden.) Solche Unterschiede existieren für alle euklidischen Vektoren.
|
Das meinte ich eigentlich nicht.
https://de.wikipedia.org/wiki/Resultierende_Kraft
Ich kann viele Resultierende bilden.
Ich kann zum Beispiel über die Summe aller BodenKräfte p(x,y)*dA eines Objektes das am Boden liegt integrieren und hätte eine Resultierende aus all diesen kleinen dFn Normalkräften, also die Resultiernde Normalkraft
Ich kann die Resultiernde von FIS1 und FIS2 bilden, was durch die Masse dividiert der daraus resultiernde ais beschleunigung entspricht, also koordinatenbeschleunigung auf x,y im Inertialsystem(abseits Gravitation),
Ich kann auch hergehen und die Resultilerende aus Summer aller Inertialsystemkräfte plus der Trägheitskraft Ft bilden dann entspricht die Resultiernde durch m der resultiernden Beschleunigung anis, Koordinatenbeschleunigung auf x',y'.
Warum sollte das Wort Resultiernde für genau die Summe aller realen Wechselwirkungskräfte reserviert sein.
Aber es ist ja eigentlich egal, denn jetzt weiß ich sowieso was gemeint ist.
| Zitat: | Hm, mir gefällt die Formulierung "weil ich die Zeitachse nicht gekrümmt betrachte" nicht. Kannst du genauer erklären, wie das gemeint ist
|
na so wie im Video Newton verse Einstein.
abseits von Gravitation kann ich die Zeitachse so wie bei Newton betrachten, mit Gravitation muß ich sie krümmen das ich im 4d Raum eine gerade erhalte für kräftefreie Körper.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 31. Dez 2018 10:40 Titel: TomS Verfasst am: 31. Dez 2018 10:40 Titel: |
 |
|
Die Zeitachse ist nicht gekrümmt; diese Aussage ist sinnlos.
Stellˋ dir eine Kugelfläche vor und überziehe sie mit infinitesimalen Vierecken. Die Seiten entsprechen den lokalen Koordinatenachsen. Diese sind offenbar nicht gekrümmt, d.h. die Krümmung steckt nicht in einer Koordinatenachsen für sich alleine.
https://en.m.wikipedia.org/wiki/Tetrad_formalism
https://en.m.wikipedia.org/wiki/Riemann_curvature_tensor
https://en.m.wikipedia.org/wiki/Curvature_of_Riemannian_manifolds
Ein wesentlicher Aspekt der Krümmung kann wie folgt definiert werden: man betrachte einen Vektor, der einen bestimmten Winkel mit einer infinitesimalen, geschlossenen Kurve einschließt, z.B. einem der o.g. infinitesimalen Vierecke. Nun verschiebt man den Vektor parallel zu sich selbst entlang dieser Kurve. Nach einem kompletten Umlauf wird der so verschobene Vektor einen nicht-verschwindenden Winkel mit dem ursprünglichen Winkel einschließen. Dieser Winkel ist ein Maß für die Krümmung der eingeschlossenen Fläche.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 02. Jan 2019 22:50 Titel: VeryApe Verfasst am: 02. Jan 2019 22:50 Titel: |
 |
|
| Zitat: | | Stellˋ dir eine Kugelfläche vor und überziehe sie mit infinitesimalen Vierecken. Die Seiten entsprechen den lokalen Koordinatenachsen. Diese sind offenbar nicht gekrümmt, d.h. die Krümmung steckt nicht in einer Koordinatenachsen für sich alleine. |
Okay ich stell mir ne Kugeloberfläche vor und darauf ein kleine viereckfläche
und eine solche Fläche was stellt die dar den 3DRaum auf 2D gepackt oder wie
ich nehm eine Kante für die x Achse eine Kante für die y Achse, und wo ist die zAchse.
Wenn sich jetzt Objekte entlang der Kugeloberfläche in der Vorstellung bewegen, dann bewegen sie sich ja erst wieder auf krummen Bahnen.
Ich dachte, ich kann den 3dRaum auf 2d mal packen, dann betrachte ich die Zeitachse so als wäre sie eine weitere Längenachse (Raumachse) und würde irgendwie für kraftlose Bewegungen wirklich eine Gerade erhalten, in der zur jedem vergangenen Zeitabschnitt auch der selbe weg zurückgelegt wird.
Gibts da kein Buch für Deppen, Ich habe mir ein Buch von Fliessbach gekauft über die ART, da versteh ich die Mathematik alleine von den Schreibweisen nicht.
Ein Buch zumindensten für komplette Anfänger zur 4D Geometrie, wo das für Deppen erklärt ist.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Jan 2019 23:14 Titel: index_razor Verfasst am: 02. Jan 2019 23:14 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
Gibts da kein Buch für Deppen, Ich habe mir ein Buch von Fliessbach gekauft über die ART, da versteh ich die Mathematik alleine von den Schreibweisen nicht.
Ein Buch zumindensten für komplette Anfänger zur 4D Geometrie, wo das für Deppen erklärt ist. |
Den Fließbach kenne ich nicht. Aber ich habe schon öfter Misner, Thorne, Wheeler, "Gravitation" empfohlen. Das Buch ist deswegen weit über 1000 Seiten dick, weil es wirklich alle benötigten mathematischen Grundlagen von Anfang an erklärt, mit Unmengen von Bildern und Boxen mit vertiefenden Betrachtungen der Themen aus dem Haupttext.
Anderer Vorschlag: Wir diskutieren deine Fragen zum Fließbach hier. An der Schreibweise sollte es wirklich nicht scheitern. (Bist du sicher, daß es nur die "Schreibweise" ist?)
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 02. Jan 2019 23:39 Titel: VeryApe Verfasst am: 02. Jan 2019 23:39 Titel: |
 |
|
| Zitat: | 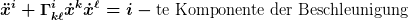 |
da verstehe ich gerade noch das 
das andere 
könnte für mich auch auf einer arabischen Speisekarten stehen, und ich glaube ich bekomme nen Gurkensalat.
Ka Ahnung was man da genau mathematisch machen muß noch für was die Symbole stehen,
also dieses empfohlene Buch kaufe ich mir
Misner, Thorne, Wheeler ... Gravitation, das ist natürlich super wenn die auch für keine Fortgeschrittenen schreiben .
danke 
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 03. Jan 2019 14:15 Titel: TomS Verfasst am: 03. Jan 2019 14:15 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
das 
könnte für mich auch auf einer arabischen Speisekarten stehen ... |
das ist auch bei Misner, Thorne & Wheeler Pflicht; ohne das geht’s nicht
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Jan 2019 14:19 Titel: index_razor Verfasst am: 03. Jan 2019 14:19 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | VeryApe hat Folgendes geschrieben: |
das 
könnte für mich auch auf einer arabischen Speisekarten stehen ... |
das ist auch bei Misner, Thorne & Wheeler Pflicht; ohne das geht’s nicht |
Sie erklären schon sehr sorgfältig was die 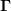 s bedeuten. Aber ganz anspruchslos ist das Buch trotzdem nicht. Man benötigt zumindest solide Kenntnisse in linearer Algebra und mehrdimensionaler Analysis würde ich sagen. Unter diesen Voraussetzungen kommt man aber mit viel Geduld schon ziemlich weit. s bedeuten. Aber ganz anspruchslos ist das Buch trotzdem nicht. Man benötigt zumindest solide Kenntnisse in linearer Algebra und mehrdimensionaler Analysis würde ich sagen. Unter diesen Voraussetzungen kommt man aber mit viel Geduld schon ziemlich weit.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18558
|
 TomS Verfasst am: 03. Jan 2019 17:57 Titel: TomS Verfasst am: 03. Jan 2019 17:57 Titel: |
 |
|
MTW ist sicher das beste Buch, wenn man ohne Vorkenntnisse bzgl. Riemannscher Geometrie, Differentialformen usw. in die ART einsteigen und sehr tief sowie in die Breite gehen möchte.
Wald m.E. für Einsteiger absolut ungeeignet.
Weinberg soll sehr gut sein, kenne ich aber selbst nicht.
Andere Bücher wie Sexl, Fließbach u.a. sind weit weniger umfassend.
Online sollten Carroll eine gute Quelle sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Jan 2019 18:42 Titel: index_razor Verfasst am: 03. Jan 2019 18:42 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | MTW ist sicher das beste Buch, wenn man ohne Vorkenntnisse bzgl. Riemannscher Geometrie, Differentialformen usw. in die ART einsteigen und sehr tief sowie in die Breite gehen möchte.
Wald m.E. für Einsteiger absolut ungeeignet.
|
Das sehe ich genauso.
| Zitat: |
Weinberg soll sehr gut sein, kenne ich aber selbst nicht.
|
Ich kenne ihn ein bißchen. Der größte Nachteil ist m.E. daß er ausschließlich im Ricci-Kalkül arbeitet und deswegen ein bißchen unmodern wirkt. Ich würde ihn daher auch nicht unbedingt als Einsteigerlektüre empfehlen. Aber ich bin bei der Form der Darstellung auch sehr voreingenommen.
|
|
 |
|
|