| Autor |
Nachricht |
t.t.
Anmeldungsdatum: 04.10.2007
Beiträge: 113
Wohnort: Konstanz
|
 t.t. Verfasst am: 18. Okt 2007 14:54 Titel: Näherungen in der Physik - die Taylorreihe t.t. Verfasst am: 18. Okt 2007 14:54 Titel: Näherungen in der Physik - die Taylorreihe |
 |
|
Hallo an alle,
ich gebe jetzt hier mal eine Antwort auf eine in einem anderen Thema gestellte Frage bezüglich der Taylor-Entwicklung, da ich denke, dass diese einen wichtigen Stellenwert in der Physik einnimmt und es (noch) keinen derartigen Thread zu dem Thema gibt.
Alle die sich schon einmal über die Näherungen in irgendwelchen Rechnungen gewundert haben (und sei es die Kleinwinkelnäherung \approx x) ), denen versuche ich hier mal zu erklären, wieso weshalb und warum es funktioniert und wo man sie verwenden kann. ), denen versuche ich hier mal zu erklären, wieso weshalb und warum es funktioniert und wo man sie verwenden kann.
Ein bisschen Mathe
Betrachtet werden soll eine stetige Funktion ) . Interessant für den Physiker (und den Mathematiker, der Analysis lernt) ist nun das Verhalten dieser Funktion um einem festen Punkt . Interessant für den Physiker (und den Mathematiker, der Analysis lernt) ist nun das Verhalten dieser Funktion um einem festen Punkt 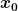 im Definitionsgebiet. im Definitionsgebiet.
Nun bietet sich eine "anschauliche" Betrachtung an. Die Funktion ) wird, da sie stetig ist, in der Nähe des Punkes wird, da sie stetig ist, in der Nähe des Punkes 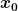 natürlich keine großen Sprünge machen. Eine erste Approximation ist also durch natürlich keine großen Sprünge machen. Eine erste Approximation ist also durch
\approx f(x_0)\qquad |x-x_0|\text{ klein})
Natürlich ist diese Approximation für viele Funktionen einfach zu ungenau, so dass man sich, wiederum geometrisch, überlegen kann, dass die Funktionswerte von ) wohl eher durch eine lineare Funktion besser approximiert wären. Also setzen wir mal wohl eher durch eine lineare Funktion besser approximiert wären. Also setzen wir mal
\approx f(x_0)+f'(x_0)(x-x_0))
was der Tangente an die Funktion ) im Punkt entspricht. im Punkt entspricht.
Eine noch bessere Approximation bildet natürlich eine quadratische oder kubische Funktionen (oder Polynome höherer Ordnung).
Genau hier hilft die Taylor-Formel mit der man den Verlauf beliebiger Funktionen in der Nähe eines Punktes mit einem Polynom approximieren kann.
Es ist
=f(x_0)+f'(x_0)(x-x_0)+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x,x0)=\sum_{k=0}^n\frac{1}{k!}f^{(k)}(x_0)(x-x_0)^k+R_n(x,x_0))
Hierbei bedeutet }(x_0)) die k-te Ableitung der Funktion f an der Stelle die k-te Ableitung der Funktion f an der Stelle 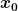 . .
Die Funktion ) , das Restglied, ist bildlich gesprochen die Abweichung der Summe (des Polynoms) zum eigentlichen Funktionsverlauf. Wers genau wissen will schaut sich mal im Matheforum um, nur soviel sei gesagt, für , das Restglied, ist bildlich gesprochen die Abweichung der Summe (des Polynoms) zum eigentlichen Funktionsverlauf. Wers genau wissen will schaut sich mal im Matheforum um, nur soviel sei gesagt, für 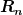 gilt: gilt: ^{n+1}) . .
Für immer höhere Ordnungen geht die Summe der Taylor-Formel in die Taylorreihe über, die ohne Restglied beliebige Funktionen approximieren kann.
=\sum_{k=0}^\infty\frac{1}{n!}f^{(n)}(x_0)(x-x_0)^n)
So genug der Mathe, jetzt mal ein Beispiel. Wir wollen die Funktion :=sin(x)) um um  etwas näher betrachten (bzw. die Winkelfunktion durch ein Polynom approximieren) etwas näher betrachten (bzw. die Winkelfunktion durch ein Polynom approximieren)
 http://lorenzt.de/PBPics/Sin_Approx.gif http://lorenzt.de/PBPics/Sin_Approx.gif
Bilder helfen beim Verständnis: Gezeichnet sind:
Die Funktionen ) gelb, die Funktion gelb, die Funktion  (grün), sowie die Funktionen (grün), sowie die Funktionen  (blau) und (blau) und  (rot). (rot).
Dies sind genau die ersten Ordnungen (also das n ab dem die Summe abgebrochen wird) der Taylorentwicklung von ) um die Stelle um die Stelle  . .
Man kann deutlich erkennen, dass die Polynome höherer Ordnung die Funktion in einem größeren Bereich besser approximieren. Taylor funktioniert 
Und für alle die's nicht glauben hier die ersten Terme der Taylorreihe:
\approx \underbrace{sin(0)}_{=0}+cos(0)\cdot x-\underbrace{\frac{sin(0)}{2}}_{=0}\cdot x^2 -\frac{\cos(0)}{6}x^3+...)
Eine andere Darstellung
Oft stolpert man über eine etwas andere Darstellung der Taylorreihe, die aber äquivalent zu der obigen ist.
=\sum_{k=0}{\infty}\frac{f^{(n)}(x_0)}{n!}(\Delta x)^n)
Oft ist es einfacher mehrere Ableitungen von Funktionen zu bestimmen als mit der gegebenen Funktion zu rechnen, da sich viele komplizierte Operationen mit einem Polynom einfacher ausführen lassen. Nun aber genug der Mathe, jetzt gehts an die Physik 
Einsatz der Taylorreihe als Hilfmittel der Physik
Die Einsatzmöglichkeiten einer Taylor-Entwicklung sind in der Physik nahezu unbegrenzt. Deshalb kann ich mich hier nur auf einige Beispiele beschränken.
Kleinwinkelnäherung
Viele haben schon eine Taylorentwicklung genutzt, ohne davon zu wissen. Die Näherungen \approx x) und und \approx 1) für kleine x basieren auf einer Taylorreihe. für kleine x basieren auf einer Taylorreihe.
Die ersten Glieder der Taylorentwickling der Winkelfunktionen sind:
\approx \underbrace{sin(0)}_{=0}+\cos(0)\cdot x+O(x^2)=x+O(x^2)\qquad \cos(x)\approx\cos(0)+\underbrace{sin(0)}_{=0}\cdot x+O(x^2)=1+O(x^2)) . .
Für kleine Winkel  sind die Terme höherer Ordnung vernachlässigbar und die Näherungen gerechtfertigt. sind die Terme höherer Ordnung vernachlässigbar und die Näherungen gerechtfertigt.
Wurzelapproximationen
Eine andere auch häufig genutzte Anwendung der Taylorentwicklung ist das Entwickeln von "schwierigen" Termen in physikalischen Rechnungen.
Ein gutes Beispiel hierfür lief mir neulich über den Weg... Nach der speziellen Realtivitätstheorie gilt die die Energie-Impuls-Beziehung.
^2+(pc)^2})
Die Gesamtenergie eines Körpers ist duch diesen Ausdruck gegeben, soch wie lässt sich dies mit der klassischen Betrachtung für kleine Impulse ( ) in Einklang bringen. Eine Taylorentwicklung für die Energie (für kleine Impulse) liefert hier ) in Einklang bringen. Eine Taylorentwicklung für die Energie (für kleine Impulse) liefert hier

Der letzte Term lässt sich für kleine Impulse vernachlässigen, so dass für kleine Impulse die klassische Form der Gesamtenergie (Summe aus der konstanten Ruheenergie und kinetischer Energie) gilt...
Multipolentwicklungen
Das letzte Beispiel einer (hier sogar mehrdimensionalen) Taylorentwicklung ist die Multipolentwicklung für elektrische Potentiale einer Ladungsverteilung. Diese sind im allgemeinen als Integral über eine Ladungsverteilung gegeben
=\frac{1}{4\pi\varepsilon_0}\int_V\dd^3r' \,\frac{\rho(\vec r')}{\|\vec r-\vec r'\|})
Dieses Integral ist im Allgemeinen nicht analytisch lösbar. Das Problem ist die "komplizierte" Ortsabhängigkeit durch den Betrag.
Die Lösung dieses Problems bietet sich durch eine Taylor-Entwicklung des Integranden. (Problematisch hierbei ist "nur" dass es sich hierbei nicht um eine eindimensionale Taylor-Entwicklung handelt. Alle die mit der Analysis in mehreren Dimensionen nicht vertraut sind können dies nur noch schwer nachvollziehen).
Die Taylor-Entwicklung des Integranden ergibt nun

(Den Quadrupol spare ich mir hier)
Nun ist das Integral relativ einfach lösbar, denn es ist
&\approx&\frac{1}{4\pi\varepsilon_0}\int_V\dd^3r' \,\rho(\vec r')\left(\frac{1}{\|\vec r\|}-\frac{\vec r'\cdot\vec r}{\|\vec r\|^3}+...\right)\\ &=&\frac{1}{4\pi\varepsilon_0}\left(\frac{1}{\|\vec r\|}\underbrace{\int_V\dd^3r' \rho(\vec r')}_{=Q}-\frac{\vec r}{\|\vec r\|^3}\cdot \underbrace{\int_V\dd^3r \rho(\vec r')\cdot \vec r'}_{=\vec p}+...\right)\\ &=&\frac{1}{4\pi\varepsilon_0}\left(\frac{Q}{\|\vec r\|}+\frac{\vec p\cdot\vec r}{\|\vec r\|^3}+...\right))
Man erhält so für eine beliebige Ladungsverteilung die Multipolentwicklung. Vorsicht bei höheren Ableitungen von Funktionen im Dreidimensionalen. Diese sind im allgemeinen nicht mehr durch Vektoren sondern duch Tensoren gegeben, so dass der Quadrupol, wie auch alle höheren Multipole nur noch durch Tensoren gegeben sind.
Zusammenfassung
Viele physikalische Näherungen beruhen auf der Taylorentwicklung schwerer Terme. Ich hoffe ich konnte (die am Anfang doch so schwer verständliche) Allzweckwaffe für Näherungen ein bisschen erläutern.
Gruß T.T.
PS: Rechtschreibefehler sind gewollt und können behalten werden 
Und sollte irgendwas wichtiges fehlen, einfach posten, so natürlich auch bei Fragen etc.
_________________
Steter Tropfen höhlt den Stein....
doch, wie kann Diskretes stetig sein ? |
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
 erkü Verfasst am: 05. Mai 2008 13:34 Titel: Re: Näherungen in der Physik - die Taylorreihe erkü Verfasst am: 05. Mai 2008 13:34 Titel: Re: Näherungen in der Physik - die Taylorreihe |
 |
|
Hi t.t.,
durch Deine Antwort zu http://www.physikerboard.de/topic,11223,-formelherleitung-e%3D1-2mv%B2-aus-spez-relativitaetstheorie.html#69738 bin ich auf Deinen Beitrag unter "Sonstiges" gestoßen.
Was mich dabei sehr verwundert, ist, daß bei mehr als 1000 Aufrufen noch niemand Deinen so wichtigen Beitrag gelobt oder auch nur "Danke" o.ä. gesagt hat.
Dieses Versäumnis möchte ich hiermit nachholen.   
Gruß erkü
PS: Eine Anmerkung zu den Winkelfunktionen habe ich noch.
 Hier sollte man noch mal ausdrücklich darauf hinweisen, daß die einzige mathematisch saubere Definition eines Winkels durch das Verhältnis von Bogenlänge zum Radius gegeben ist. Hier sollte man noch mal ausdrücklich darauf hinweisen, daß die einzige mathematisch saubere Definition eines Winkels durch das Verhältnis von Bogenlänge zum Radius gegeben ist.
Daß also "Altgrad" oder "Neugrad" oder sonstige obskuren "Winkeleinheiten" mit der Mathematik nichts zu tun haben.
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk: |
|
 |
Freak19
Anmeldungsdatum: 16.05.2008
Beiträge: 5
|
 Freak19 Verfasst am: 23. Mai 2008 17:50 Titel: Freak19 Verfasst am: 23. Mai 2008 17:50 Titel: |
 |
|
Ein bisschen Lob hat noch keinem geschadet.
Absolut klasse gemachter Beitrag Danke. |
|
 |
knoblauchpresse
Anmeldungsdatum: 30.08.2009
Beiträge: 3
|
 knoblauchpresse Verfasst am: 31. Aug 2009 18:05 Titel: Re: Näherungen in der Physik - die Taylorreihe knoblauchpresse Verfasst am: 31. Aug 2009 18:05 Titel: Re: Näherungen in der Physik - die Taylorreihe |
 |
|
| erkü hat Folgendes geschrieben: | | Was mich dabei sehr verwundert, ist, daß bei mehr als 1000 Aufrufen noch niemand Deinen so wichtigen Beitrag gelobt oder auch nur "Danke" o.ä. gesagt hat. |
Und ich muss das gleich mal nachholen: Hab mich hier angemeldet, weil ich mit einer Aufgabe nicht weiter kam, Artikel überflogen: Wurzelapproximation (hab mich die ganze Zeit gewundert, wie ich nen hässlichen Wurzelausdruck wegbekomm) und...... *stirnpatsch* da kam die Erleuchtung 
Danke dafür  |
|
 |
Mathe-Noob
Gast
|
 Mathe-Noob Verfasst am: 02. Jan 2010 17:34 Titel: Mathe-Noob Verfasst am: 02. Jan 2010 17:34 Titel: |
 |
|
hallo,
ich schreibe meine Mathematik-Facharbeit (schule) über die Taylorreihen und ihre Anwendung in der Physik, leider tappe ich derzeit total im Dunklen, was passende Bücher zu diesem Thema angeht.. Mir fehlen also Physik-Lehrbücher, in denen die praktische Anwendung (relativ) ausführlich beschrieben ist..
Deshalb wollte ich fragen, ob vielleicht jemand von euch mehr Ahnung hat als ich  |
|
 |
Quantenfrost
Anmeldungsdatum: 14.06.2010
Beiträge: 9
|
 Quantenfrost Verfasst am: 15. Jun 2010 17:06 Titel: Quantenfrost Verfasst am: 15. Jun 2010 17:06 Titel: |
 |
|
du kannst mit tayler eine beliebig komplizierte fnkt beliebig einfach machen.
dabei schreibst du zb den sinus als reihe auf...
man betrachte sinus an der stelle null und möchte nun die steigung in kleiner umgebung betrachten. die steigung kannst du mit einem geodreieck berechnen. einfach bei x=0 anlegen und kästchen zählen. damit weißt du die steigung von sin(x) bei x=0 ist 1. für kleine umgebung ist das richtig aber wenn dein lehrer die umgebung größer haben möchte musst du weiter hinschauen da es abweichungen gibt
also legst du auf deine funktion Tayler T(x)=x noch die
f(x)= -x³ auf den sinus damit es in größeren bereichen immernoch stimmt.
der rest der taylerreihe sind schönheitskorrekturen damit es in immer größerer näherung noch stimmt. zB reicht ein T(x)= x-x³ nicht aus sondern du musst dein x³ noch durch 6, also 3!, teilen
dafür gibt es dann die formel die schon ganz oben steht[/img]
_________________
Sei ɛ < 0 |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 15. Jun 2010 18:25 Titel: DrStupid Verfasst am: 15. Jun 2010 18:25 Titel: |
 |
|
| Quantenfrost hat Folgendes geschrieben: | | du kannst mit tayler eine beliebig komplizierte fnkt beliebig einfach machen. |
Das ist zwar ein bewährtes Verfahren, aber man muss dazu sagen, dass es nur in der Umgebung eines Punktes funktioniert. Will man die Funktion dagegen innerhalb eines Intervalls approximieren, dann sollte man lieber versuchen, das Integral der quadratischen Abweichung zu minimieren. Der Aufwand ist zwar erheblich größer, aber dafür ist das Ergebnis oft mehr als eine Größenordnung besser (gemessen an der maximalen Abweichung oder am Integral der quadratischen Abweichung). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 15. Jun 2010 22:30 Titel: TomS Verfasst am: 15. Jun 2010 22:30 Titel: |
 |
|
| Quantenfrost hat Folgendes geschrieben: | | du kannst mit tayler eine beliebig komplizierte fnkt beliebig einfach machen. |
Das stimmt so nicht.
Bsp.: man kann zwar die Funktion
 = \frac{1}{1-x} = 1 + x + x^2 + \ldots = \sum_{n=0}^\infty x^n)
in eine Taylorreihe um x=0 entwickeln, aber diese konvergiert (wegen der Singularität bei x=1) nur für |x| < 1.
Ein weiteres Bsp.: die Funktion
 = e^{-1/x^2})
kann für x=0 nicht in eine Taylorreihe entwickelt werden; jeder Term der Taylorentwicklung ist identisch Null:
}(x=0) = 0)
Man versteht dieses Verhalten, wenn man die Funktion im Komplexen, d.h. für z=x+iy betrachtet und nun x=0 setzt; man erhält
 = e^{1/y^2})
D.h. dass der Grenzwert
)
nicht existiert.
D.h. man muss die zu entwickelnde Funktion im Komplexen untersuchen, um die Existenz sowie die Eigenschaften (Konvergenz) ihrer Taylorreihe zu verstehen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 03. Jul 2012 23:18 Titel: kingcools Verfasst am: 03. Jul 2012 23:18 Titel: |
 |
|
ODER man sagt, dies gilt genau dann, wenn das Restglied verschwindet, was bei dem Beispiel f(x) = exp(-1/x²) mit f(x<=0) = 0 nicht der Fall ist.
Ferner ist im Eingangspost die Näherung
f(x) ca. = f(x0)* |x-x0| schlicht unsinn, die stimmt ja nicht mal bei x = x0, sofern f(x0) ungleich Null ist. |
|
 |
|
|




















 Hier sollte man noch mal ausdrücklich darauf hinweisen, daß die einzige mathematisch saubere Definition eines Winkels durch das Verhältnis von Bogenlänge zum Radius gegeben ist.
Hier sollte man noch mal ausdrücklich darauf hinweisen, daß die einzige mathematisch saubere Definition eines Winkels durch das Verhältnis von Bogenlänge zum Radius gegeben ist.

