| Autor |
Nachricht |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 16. Jan 2010 14:54 Titel: Berechnung der Resonanzfrequenz eines Parallelschwingkreises Veryyy Verfasst am: 16. Jan 2010 14:54 Titel: Berechnung der Resonanzfrequenz eines Parallelschwingkreises |
 |
|
Hallo,
ich möchte die Resonanzfrequenz eines Parallelschwingkreises mit einer Spule, einem Kondensator und einem ohmschen Widerstand berechnen.
Also alle parallel.
Dazu habe ich so angesetzt
 . .
Da man bei Parallelschwingkreisen ja mit dem Leitwert rechnet.
Dies habe ich berechnet, im Nenner mit der 3. binomischen Formel ergänzt, dass das i aus dem Nenner fällt und dann den Imaginärteil des ganzen =0 gesetzt, da dies ber bei der Resonanzfrequenz ja Null wird.
Damit bin ich auf  gekommen. gekommen.
Stimmt das so?
Was mich verwundert, ist dass ich bei der Rechnung für die Resonanzfrequenz für alle drei Bauteile in einem Serien- also Reihenschwingkreis auf genau dasselbe Ergebnis für die Resonanzfrequenz gekommen bin. Das hat mich etwas irritiert. Kann das sein, oder gibt es dafür eine physikalische Erklärung?
Ich hänge mal noch die gesamte Rechnung für die Resonanzfrequenz des Parallelschwingkreises an, falls da das Ergebnis falsch sein sollte.
Ich würde mich über Antworten sehr freuen.
Gruß,
Veryyy
| Beschreibung: |
|
| Dateigröße: |
28.63 KB |
| Angeschaut: |
20323 mal |
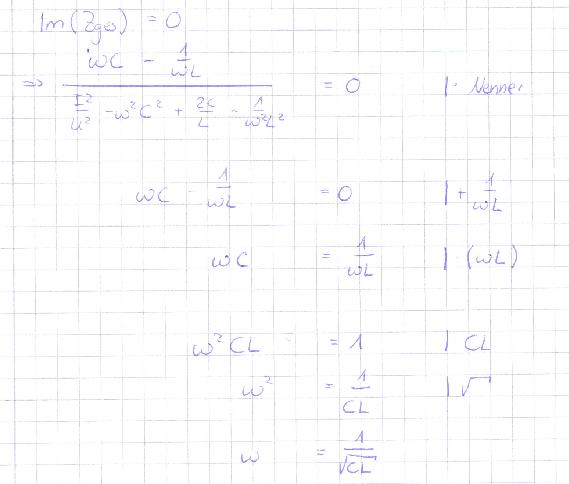
|
| Beschreibung: |
|
| Dateigröße: |
40.72 KB |
| Angeschaut: |
16362 mal |

|
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 16. Jan 2010 16:06 Titel: GvC Verfasst am: 16. Jan 2010 16:06 Titel: |
 |
|
Warum eine so komplizierte Rechnung? Die Bedingung für den Resonanzfall ist doch, dass die Schaltung nur Wirkleistung aufnimmt, d.h. dass Re(Z) = 0, was aber gleichbedeutend ist mit Re(Y) = 0. Also hättest Du auch schreiben können:
Y = 1/R - j/wL + jwC = 1/R + j(wC - 1/wL)
Wenn hier der Imaginärteil Null gesetzt wird, ergibt sich natürlich dasselbe wie beim Nullsetzen des Imaginärteils des Widerstandes in der Reihenschaltung.
Reihenschaltung Z = R + jwL - j/wC = R + j(wl -1/wc)
Obwohl die Resonanzfrequenz bei Reihen- und Parallelschaltung dieselbe ist, gibt es doch einen gravierenden Unterschied: In der Reihenschaltung ist bei Resonanzfrequenz der Blindwiderstand Null (d.h. der Blindleitwert ist unendlich groß), in der Parallelschaltung ist bei Resonanzfrequenz der Blindleitwert Null (d.h. der Blindwiderstand unendlich groß). Bei konstanter Gesamtspannung U ist in der Reihenschaltung die aufgenommene Wirkleistung im Resonanzfall maximal, nämlich P = U²/R, in der Parallelschaltung ist die aufgenommene Wirkleistung P = U²/R unabhängig von der Frequenz, also unabhängig davon, ob Resonanz vorliegt oder nicht.
|
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 17. Jan 2010 16:06 Titel: Veryyy Verfasst am: 17. Jan 2010 16:06 Titel: |
 |
|
Vielen Dank erst mal für deine Antwort.
Das freut mich, dass du dasselbe Ergebnis raushast.
Was ich nicht wusste ist, dass gilt =0\Leftrightarrow Re(Y)=0)
Gehe ich richtig in der Annahme, dass Y der Leitwert ist? Also  ? ?
Deshalb habe ich auch die komplizierte Rechnung, weil bei mir der gesamte Teil dann im Nenner stand und ich das ja erst in den Zähler bekommen musste.
Warum gilt denn, dass =0\Leftrightarrow Re(Y)=0) ? Gilt das immer oder nur in diesem Fall? ? Gilt das immer oder nur in diesem Fall?
| Zitat: | | In der Reihenschaltung ist bei Resonanzfrequenz der Blindwiderstand Null (d.h. der Blindleitwert ist unendlich groß), in der Parallelschaltung ist bei Resonanzfrequenz der Blindleitwert Null (d.h. der Blindwiderstand unendlich groß) |
hmm, das habe ich noch nicht so ganz verstanden. Ich dachte, wenn der Imaginärteil =0 ist, müssen sich der Widerstand von Spule und Kondensator genau aufheben. Also im Diagramm müssen die Pfeile dann gleich lang sein, sodass sie sich wegheben. Wenn aber bei der Parallelschaltung der Blindwiderstand unendlich groß ist, kann doch der Imaginärteil nie =0 werden, oder?
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 17. Jan 2010 16:37 Titel: GvC Verfasst am: 17. Jan 2010 16:37 Titel: |
 |
|
| Veryyy hat Folgendes geschrieben: | | Wenn aber bei der Parallelschaltung der Blindwiderstand unendlich groß ist, kann doch der Imaginärteil nie =0 werden, oder? |
In einer Parallelschaltung ist der Gesamtleitwert gleich der Summe der Einzelleitwerte. Wenn der Leitwert also Null ist (Resonanzfall), ist der Widerstand der Kehrwert davon, also unendlich groß. Es bleibt bei der Parallelschaltung von R, L und C im Resonanzfall nur 1/G = R übrig.
Im Übrigen: Ich hatte einen Fehler gemacht. Überall wo ich Re() = 0 geschrieben habe, soltte es Im() = 0 heißen, wie es ja auch aus dem weiteren Zusammenhang hervorging. Sorry! Dennoch stimmt die Folgerichtigkeit, dass Re(Z) = 0 gleichbedeutend ist mit Re(Y) = 0. Wenn Du von einem reinen Blindwiderstand den Kehrwert nimmst, hat dann der Leitwert einen Realteil? Nein? Na also! Dann ist Re(Z) = 0 gleichbedeutend mit Re(Y) = 0.
In Deiner Aufgabe ging es aber um den Resonanzfall, also Im(Z) = 0, was gleichbedeutend mit Im(Y) = 0.Der Kehwert einer rein ohmschen Größe ist natürlich auch rein ohmsch.
|
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 17. Jan 2010 17:14 Titel: Veryyy Verfasst am: 17. Jan 2010 17:14 Titel: |
 |
|
oh, na klar.. hier ging es ja um den Imaginärteil, der = 0 sein soll, wegen dem Resonanzfall. Wenn ich also eine imaginäre Zahl habe a+bi Und es gilt b=0, dann ist auch 1/b = 0. Also wenn der Imaginärteil =0 ist, ist auch der Kehrwert des Imaginärteils =0. Richtig?
Und damit reicht es für mich zu zeigen, für welches omega der Imaginärteil des Leitwerts bei der Parallelschaltung = 0 wird, da damit auch der Imaginärteil an sich = 0 ist.
| Zitat: | | In einer Parallelschaltung ist der Gesamtleitwert gleich der Summe der Einzelleitwerte. Wenn der Leitwert also Null ist (Resonanzfall), ist der Widerstand der Kehrwert davon, also unendlich groß |
Ja, das habe ich jetzt verstanden.
| Zitat: | | Es bleibt bei der Parallelschaltung von R, L und C im Resonanzfall nur 1/G = R übrig. |
ist hier G gleich die Summe der Einzelleitwerte?
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 17. Jan 2010 18:20 Titel: GvC Verfasst am: 17. Jan 2010 18:20 Titel: |
 |
|
| Veryyy hat Folgendes geschrieben: | | ist hier G gleich die Summe der Einzelleitwerte? |
Nein, die Summe der Einzellleitwerte ist
Y = jwC -j/wL + G
Wenn allerdings der Imaginärteil Null ist, bleibt als Leitwert G oder als Widerstand 1/G = R übrig.
| Veryyy hat Folgendes geschrieben: | | Und es gilt b=0, dann ist auch 1/b = 0 |
Das kann ja wohl nicht sein. Die einzige Zahl, die ihrem Kehrwert gleich ist, ist die Zahl 1.
1/0 erhält man durch Grenzwertbildung zu "unendlich".
Das war hier aber nicht die Frage. Wenn bei a + jb der Imaginärteil Null ist, also b = 0, dann hat der Kehrwert 1/(a+jb) ebenfalls keinen Imaginärteil, den bei b = 0 ist 1/(a+jb) = 1/a, also rein reell.
|
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 17. Jan 2010 19:56 Titel: Veryyy Verfasst am: 17. Jan 2010 19:56 Titel: |
 |
|
| Zitat: | | Wenn bei a + jb der Imaginärteil Null ist, also b = 0, dann hat der Kehrwert 1/(a+jb) ebenfalls keinen Imaginärteil, den bei b = 0 ist 1/(a+jb) = 1/a, also rein reell. |
Ach so. Jetzt ist mir die Sache klar. Und das omega habe ich ja auch berechnet (einmal kompliziert und einmal einfach mit deinem Tipp  ) Also alle Fragen gelöst. ) Also alle Fragen gelöst.
Vielen Dank für deine Hilfe.
|
|
 |
|
|
















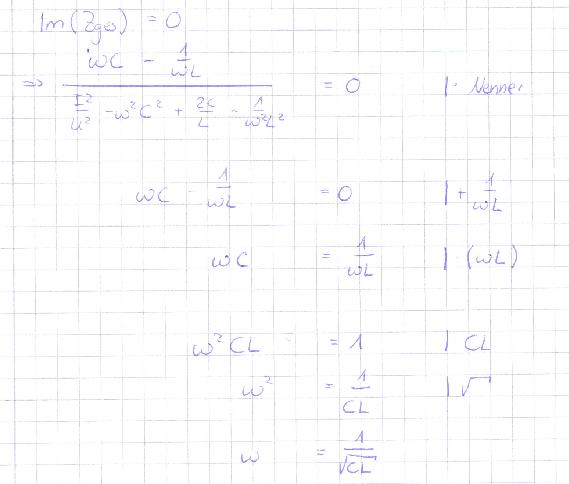

 ) Also alle Fragen gelöst.
) Also alle Fragen gelöst.