| Autor |
Nachricht |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 31. März 2009 16:46 Titel: Schwingungsdauer beim Fadenpendel Ricky Verfasst am: 31. März 2009 16:46 Titel: Schwingungsdauer beim Fadenpendel |
 |
|
hallöchen zusammen,
also wir haben heute einen versuch gemacht.
und zwar sollten wir an einem faden gewichte dranhägen
und diesen pendeln lassen.
dann haben mit der stoppuhr die zeit für eine schwingung gemessen.
anschließend haben wir dann eine tabelle gemacht und die länge
gegen die zeit aufgetragen.
daraus sollten wir nun ein diagramm erstellen.
bei diesem kam ein parabelförmiger graph raus.
und nun sollen wir daraus schließen ,wie man die periodendauer
berechnet.
nun ich kenne die formel schon sie lautet doch  nicht wahr? nicht wahr?
nun hat meine lehrerin uns nur folgenden tip gegeben:

das hilft mir aber irgendwie auch nicht weiter...
kann mir bitte jemand helfen?
vielen lieben dank! 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 31. März 2009 17:45 Titel: Ricky Verfasst am: 31. März 2009 17:45 Titel: |
 |
|
Bitte gib hier Deine Frage ein. Welche Lösungsansätze sind Dir selbst dazu eingefallen? Was hast Du schon probiert? Bedenke, dass wir hier Hilfe zur Selbsthilfe leisten und keine Komplettlösungen liefern werden. Viel Erfolg!
Zuletzt bearbeitet von Ricky am 06. Jun 2009 12:02, insgesamt 2-mal bearbeitet |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 31. März 2009 17:58 Titel: as_string Verfasst am: 31. März 2009 17:58 Titel: |
 |
|
Anscheinend will sie damit sagen: Wenn bei gleichem Auslenkungswinkel der Faden um den Faktor k länger ist, dann ist die Höhe um den selben Faktor größer, also auch die Energie im Pendel. Bei k-facher Energie ist die Geschwindigkeit am tiefsten Punkt dann aber nur um  größer, eben wegen der Gleichung, die aus der Energieerhaltung ja direkt herleitbar ist. Wenn man nun annimmt, dass die Geschwindigkeit überall um den Faktor größer, eben wegen der Gleichung, die aus der Energieerhaltung ja direkt herleitbar ist. Wenn man nun annimmt, dass die Geschwindigkeit überall um den Faktor  größer ist (also auch die Durchschnittsgeschwindigkeit größer ist (also auch die Durchschnittsgeschwindigkeit 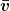 ), aber die Strecke, die der Körper vom einen Maximalausschlag zum anderen zurück legen muss um den Faktor ), aber die Strecke, die der Körper vom einen Maximalausschlag zum anderen zurück legen muss um den Faktor 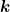 größer wird, dann könnte man sich zumindest plausibel machen, dass das Pendel dann auch länger braucht, und zwar gerade um den Faktor größer wird, dann könnte man sich zumindest plausibel machen, dass das Pendel dann auch länger braucht, und zwar gerade um den Faktor  . .
Aber das ist keine echte Herleitung/Beweis. Ich wüsste aber auch nicht, was sonst gemeint sein könnte.
Übrigens: Warum macht man denn so einen Thread in "Elektrik" auf? Das ist doch eindeutig Mechanik. Ich hab das mal verschoben.
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 31. März 2009 18:05 Titel: Ricky Verfasst am: 31. März 2009 18:05 Titel: |
 |
|
danke,dass du den thread verschoben hast.
da ist mir wohl ein fehler unterlaufen.
naja,also ich weiß nicht so recht wir sollen
die formel herleiten haben aber bisher nur den
tip mit der kinetischen und potentiellen energie.
weiss jemand wie ich damit die formel herleiten kann?
danke! 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 31. März 2009 19:11 Titel: Ricky Verfasst am: 31. März 2009 19:11 Titel: |
 |
|
ich meine wie kommt man denn plötzlich auf
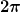
und wie stellt man die beziehung zur länge l her?

|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 31. März 2009 19:16 Titel: as_string Verfasst am: 31. März 2009 19:16 Titel: |
 |
|
Wenn Du eine Herleitung haben willst, dann schau Dir am besten den Wikipedia-Artikel zum Fadenpendel an. Aber da bringt der Tipp mit der Energie mE wenig.
Gruß
Marco
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 31. März 2009 19:37 Titel: Ricky Verfasst am: 31. März 2009 19:37 Titel: |
 |
|
die seite hab ich mir ja auch schon angeschaut
und viele andere im netz.
aber das ist alles so ein fach-chinesisch.
deshalb hab ich gehofft,dass mir das hier jemand
verständlich erklären könnte.
wenn der tip mit der energie schwachsinnig von meiner
lehrerin war ist ja egal
kann mir denn jemand die herleitung erklären (auch ohne den tip mit den energien)?
vielen lieben dank schonmal! 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 31. März 2009 21:23 Titel: Ricky Verfasst am: 31. März 2009 21:23 Titel: |
 |
|
ist da jemand der mir das so verständlich wie möglich
erklären könnte,bitte? 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 01. Apr 2009 16:59 Titel: Ricky Verfasst am: 01. Apr 2009 16:59 Titel: |
 |
|
...  .... ....
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 01. Apr 2009 17:43 Titel: schnudl Verfasst am: 01. Apr 2009 17:43 Titel: |
 |
|
Soo schwer ist das auch wieder nicht:
Du weisst ja dass die Geschwindigkeit sinusförmig verläuft. Am linken Umkehrpunkt ist sie Null, unten ist sie maximal und am rechten Umkehrpunkt wieder Null. Dazwischen liegt eine halbe Schwingungsperiode T/2.
*)
Was ist denn der Mittelwert der Geschwindigkeit während dieser Zeit, wenn das Maximum gegeben ist? Zeichne es unbedingt auf! Durch eine sehr sehr elementare Integration kannst du den Mittelwert bekommen. Er ist

*)
Und was ist daher die zurückgelegte Wegstrecke in dieser Zeit?
Die Wegstrecke in einer bestimmten Zeit ist ja mittlere Geschwindigkeit * Zeit...
Nun noch alles kombinieren (hier liegt die Herausforderung) und du bist fertig - und das alles (fast) ohne höhere Mathematik.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 01. Apr 2009 18:14 Titel: Ricky Verfasst am: 01. Apr 2009 18:14 Titel: |
 |
|
tut mir leid schnudl
aber das hab ich nicht so recht verstanden...
könntest du mir das nochmal etwas verständlicher
erklären,bitte  
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 01. Apr 2009 20:35 Titel: schnudl Verfasst am: 01. Apr 2009 20:35 Titel: |
 |
|
Ich kann dir nur eine Beweisskizze geben:
Wenn das Pendel um den Winkel  schwingt, wie gross ist dann die maximale Höhe? schwingt, wie gross ist dann die maximale Höhe?
Aus einer geometrischen Überlegung kann man sehen, dass die Höhendifferenz (1)
)
ist.
Für kleine Winkel ist (2)

daher wird

Die maximale Geschwindigkeit aufgrund der Energieerhaltung ist daher (3)

Nun betrachte den Schwingungsvorgang vom linken Winkelmaximum zum rechten Winkelmaximum. Wenn du (fälschlicherweise) eine konstante Geschwindigkeit v annimmst, dann wäre die Zeit die das Pendel dafür benötigte

Wenn man dann annimmt dass das v eben gleich der maximalen Geschwindigkeit ist (das stimmt eben nicht, aber ...), dann wird daraus
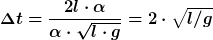
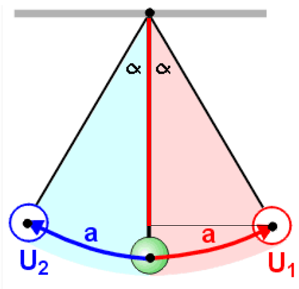
Nun, wie gesagt ist die Geschwindigkeit natürlich nicht konstant, sondern ist zuerst Null (links), wird dann maximal (unten) und wieder Null (rechts). Das sieht so aus wie im Bild, das du hättest zeichnen sollen. Es sieht aus wie eine cos-Halbwelle mit Amplitude  . Man zeigt leicht, dass der Mittelwert dieses Verlaufs (4) . Man zeigt leicht, dass der Mittelwert dieses Verlaufs (4)

ist. Die mittlere Geschwindigkeit ist also um den Faktor  kleiner als unsere angenommene konstante Geschwindigkeit, also ist die berechnete Zeitspanne um diesen Faktor grösser (5): kleiner als unsere angenommene konstante Geschwindigkeit, also ist die berechnete Zeitspanne um diesen Faktor grösser (5):

Da diese Zeit genau einer halben Schwingungsperiode entspricht, erhalten wir schliesslich


_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe)
Zuletzt bearbeitet von schnudl am 02. Apr 2009 07:15, insgesamt 2-mal bearbeitet |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 01. Apr 2009 21:59 Titel: Ricky Verfasst am: 01. Apr 2009 21:59 Titel: |
 |
|
tut mir wirklich leid schnudl.
aber ich habe schon den ersten schritt nicht verstanden,den
du gemacht hast...
ich weiss ,dass du dir viel mühe machst mir das zu erklären,
aber ich habs leider noch nicht verstanden.
kann man die herleitung denn auch irgendwie über den energie
ansatz machen?
ich hab mal eine zeichnung gemacht ,wie ich mir das so vorstelle.
vielleicht hilft uns die ja weiter und du kannst mir anhand dessen
besser helfen.
vielen dank aber schonmal 
ich weiss deine mühe zu schätzen 
Zuletzt bearbeitet von Ricky am 06. Jun 2009 12:06, insgesamt einmal bearbeitet |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 01. Apr 2009 22:05 Titel: Ricky Verfasst am: 01. Apr 2009 22:05 Titel: |
 |
|
und dann ist es doch so,dass dem pendel
zunächst potentielle energie zugefügt wird
und dieser diese dann in kinetische energie umwandelt.
also gilt doch:

nun komm ich aber nicht weiter...
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 01. Apr 2009 22:52 Titel: schnudl Verfasst am: 01. Apr 2009 22:52 Titel: |
 |
|
Vielleicht hilft dir die Skizze beim ersten Schritt (1).
Der zweite Schritt (2) ist eine Näherungsforml für den cos für kleine Winkel. Hast du von Taylorreihen schon gehört?
| Zitat: | kann man die herleitung denn auch irgendwie über den energie
ansatz machen? |
Im Dritten Schritt (3) wird die Energieerhaltung verwendet um aus der aus (1) hergeleiteteten Höhendifferenz die Maximalgeschwindigkeit zu kriegen.
Im Schritt (4) ist der eigentliche Trick. Wenn wir wissen dass die Schwingung sinusförmig verläuft, lässt sich die mittlere Geschwindigkeit über eine Halbperiode durch die Maximalgeschwindigkeit ausdrücken.
Das wird verwendet um im Schritt (5) die Zeit für eine Halbschwingung auszurechnen.
Es sind vielleicht einige Schritte hintereinander, aber kompliziert ist es keineswegs...
PS: besser ginge es mit der Lösung der Differenzialgleichung...
| Beschreibung: |
|

Download |
| Dateiname: |
pendel.png |
| Dateigröße: |
55.14 KB |
| Heruntergeladen: |
10858 mal |
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 02. Apr 2009 16:38 Titel: Ricky Verfasst am: 02. Apr 2009 16:38 Titel: |
 |
|
ok vielen dank zunächst.
aber ich vestehe erst einmal garnicht
die gleichung der höhendifferenz.
und was ist überhaupt mit höhendifferenz
bezogen auf den pendel gemeint?
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 02. Apr 2009 16:57 Titel: as_string Verfasst am: 02. Apr 2009 16:57 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | und was ist überhaupt mit höhendifferenz
bezogen auf den pendel gemeint? |
Na, die Pendelmasse hat während der Pendelbewegung doch eine sich ständig ändernde Höhe. Und was eine Differenz ist, wirst Du Dir wohl noch denken können. Es geht doch um die potentielle Energie aus der Höhe bei maximalem Ausschlag und am tiefsten Punkt. Aus diesem Höhenunterschied (=Höhendifferenz) kannst Du Dir ausrechnen, wie viel potentielle Energie in kinetische umgewandelt wurde.
Gruß
Marco
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 02. Apr 2009 17:01 Titel: Ricky Verfasst am: 02. Apr 2009 17:01 Titel: |
 |
|
ok vielen dank.
jetzt hab ich das schon mal verstanden.
mich hat das nur etwas verwirrt,
da die fäden beide neben einander gezeichnet sind.
und dann gibt es ja keine höhendifferenz.
die gibt es doch nur wenn sich der faden aus der ruhelage
bewegt,oder?
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 02. Apr 2009 17:09 Titel: Ricky Verfasst am: 02. Apr 2009 17:09 Titel: |
 |
|
so dachte ich es...
| Beschreibung: |
|

Download |
| Dateiname: |
vko02_547.jpg |
| Dateigröße: |
16.1 KB |
| Heruntergeladen: |
5565 mal |
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 02. Apr 2009 19:26 Titel: schnudl Verfasst am: 02. Apr 2009 19:26 Titel: |
 |
|
nein, merkst du denn nicht, dass die Fadenlänge immer gleich bleibt???
Wie kommst du darauf, die rechte Lange mit cos zu multiplizieren? Was ich meinte ist jene Distanz, die ich mit den Pfeilen rechts angedeutet habe: es ist jene Höhe die ein mit alpha ausgelenktes Pendel der Länge L in Bezug auf den nicht ausgelenkten Fusspunkt hat. Die Differenz der potenziellen Energie wird in kinetische Energie umgewandelt...
Das ist doch wirklich nicht so schwer...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 02. Apr 2009 19:36 Titel: Ricky Verfasst am: 02. Apr 2009 19:36 Titel: |
 |
|
ja aber so meinte ich das ja auch.
in meiner zeichnung meinte ich es so:
die linie in lila ist das ausgelenkte pendel mit dem winkel
alpha. die blaue linie soll das pendel darstellen, welches nicht ausgelenkt
ist, also ruht....ist doch richtig so...oder?
hast du meine zeichnung vielleicht nur falsch verstanden?
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 02. Apr 2009 20:00 Titel: schnudl Verfasst am: 02. Apr 2009 20:00 Titel: |
 |
|
naja, du hast die Länge des ausgelenkten Pendels mit

bezeichnet. Wenn du nur die Vertikalkomponente gemeint hast , dann stimmt es natürlich. Aber jeder der deine Skizze sieht würde sofort einen Fehler annehmen. Noch dazu hast du einen Pfeil dazugemacht, der auf den Faden zeigt.
OK, wenn du den ersten Teil verstanden hast, kannst du ja den Rest versuchen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 02. Apr 2009 20:19 Titel: Ricky Verfasst am: 02. Apr 2009 20:19 Titel: |
 |
|
das was ich jetzt noch nicht so ganz verstanden habe ist:
warum gilt : 
und warum gilt für den mittelwert des verlaufs:

??? 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 02. Apr 2009 21:24 Titel: schnudl Verfasst am: 02. Apr 2009 21:24 Titel: |
 |
|
| Ricky hat Folgendes geschrieben: | das was ich jetzt noch nicht so ganz verstanden habe ist:
warum gilt : 
Weisst du wie man die Bogenlänge ausrechnet, wenn man den Radius und den Winkel gegeben hat?
Die Zeit ist dann t = s/v = Bogenlänge / Geschwindigkeit
und warum gilt für den mittelwert des verlaufs:

???  |
Nur wenn du bereits integrieren kannst:
Der Mittelwert einer Funktion im Intervall x1 bis x2 ist
 = \frac{1}{x_2-x_1} \cdot \int_{x_1}^{x_2} y(x) \dd x)
Wir wollen den Mittelwert von
 )
im Intervall

also
 \, \dd \varphi = \frac{\hat v}{\pi} (\sin \varphi )|_{-\pi /2}^{+\pi/2} = 2 \hat v / \pi)
Das ist der einzige Schritt der nicht ganz so elementar ist.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 02. Apr 2009 21:28 Titel: Ricky Verfasst am: 02. Apr 2009 21:28 Titel: |
 |
|
ok vielen lieben dank !
du hast mir wirklich sehr geholfen! 
(also wie immer  ) ) 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 02. Apr 2009 22:14 Titel: Ricky Verfasst am: 02. Apr 2009 22:14 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: |
Weisst du wie man die Bogenlänge ausrechnet, wenn man den Radius und den Winkel gegeben hat?
|
nun hab ich doch noch eine frage.
und zwar berechnet man die bogenlänge doch folgendermaßen:

in diesem fall wäre 
doch 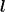
???
warum ist es bei dir denn 
??? 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 03. Apr 2009 07:23 Titel: schnudl Verfasst am: 03. Apr 2009 07:23 Titel: |
 |
|
Es ist nicht 2l, aber der Winkel geht von  bis bis  , da ich mit , da ich mit  den Winkel der maximalen Auslenkung bezeichnet und die Strecke vom linken bis zum rechten Maximum betrachtet habe. Daher ist der Gesamtwinkel den Winkel der maximalen Auslenkung bezeichnet und die Strecke vom linken bis zum rechten Maximum betrachtet habe. Daher ist der Gesamtwinkel  und die Bogenlänge und die Bogenlänge

_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 03. Apr 2009 20:20 Titel: Ricky Verfasst am: 03. Apr 2009 20:20 Titel: |
 |
|
ok.vielen dank!
war nur etwas verwirrend.
du hast in der formel also nur die 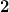
vorangestellt.
Zuletzt bearbeitet von Ricky am 06. Jun 2009 12:07, insgesamt einmal bearbeitet |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 03. Apr 2009 21:00 Titel: Ricky Verfasst am: 03. Apr 2009 21:00 Titel: |
 |
|
jetzt stellt sich mir doch nochmal eine frage.
und zwar nochmal zur höhendifferenz.
wieso lautet die formel dazu :
)
ich meine bei einer differenz sollte doch irgendwie
auch eine differenz gebildet werden,oder?
also ich verstehe jetzt ,was mit der höhendifferenz gemeint
ist und wie diese zustande kommt aber irgendwie versteh ich die
formel dazu noch nicht so ganz... 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 04. Apr 2009 11:27 Titel: Ricky Verfasst am: 04. Apr 2009 11:27 Titel: |
 |
|
ok ,das hab ich dann jetzt auch verstanden.
man kann das ja über den kosinussatz machen.
denn dieser lautet ja :

also gilt : 
da  und und 
ist : 
und dann die differenz.
ist doch dann korrekt so,oder?
nur eine frage noch wieso wählt man cosinus und nicht sinus?
denn über die sinus beziehung hätte man doch auch ohne umstellen
der gleichung ein ergebnis bekommen...? 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 04. Apr 2009 14:04 Titel: schnudl Verfasst am: 04. Apr 2009 14:04 Titel: |
 |
|
Ja genau, ...
aber wieso der Sinus? Der Sinus entspricht der Gegenkathete, also dem schwarzen Strich der über deinen roten rechten "a" steht. Diese Länge hilft uns doch überhaupt nicht weiter was die Höhendifferenz angeht - oder?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 04. Apr 2009 14:34 Titel: Ricky Verfasst am: 04. Apr 2009 14:34 Titel: |
 |
|
ach ja stimmt.
mit dem sinus wäre das doch folgendermaßen:

da  und und 
gilt: 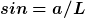
und da wir die Beziehung zu der Ankathete  benötigen hilft der sinussatz nicht weiter. benötigen hilft der sinussatz nicht weiter.
hab ich das so richtig verstanden?
vielen dank nochmal an dich 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 04. Apr 2009 14:48 Titel: Ricky Verfasst am: 04. Apr 2009 14:48 Titel: |
 |
|
Und dann hab ich noch eine Frage.
Wir hatten im Unterricht die Aufgabe:
Konstruiere ein Pendel, das mit der Periodendauer
T = 1 sek. , T = 2 sek. und T = 3 sek. schwingt.
Dazu habe ich dann die Formel 
umgestellt, zu:
²)
dann habe ich eingesetzt und folgende Längen erhalten.
Bei T = 1 sek. 
Bei T = 2 sek. 
Bei T = 3 sek. 
stimmen diese Werte ?
vielen dank nochmals 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 04. Apr 2009 17:07 Titel: schnudl Verfasst am: 04. Apr 2009 17:07 Titel: |
 |
|
so ca zumindest. da hast entweder ziemlich ungenau gerechnet oder ...
1s 0.25 m
2s 0.99m
3s 2.24m
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 04. Apr 2009 20:42 Titel: Ricky Verfasst am: 04. Apr 2009 20:42 Titel: |
 |
|
ok.vielen dank
aber mein taschenrechner zeigt mir
gerundet wirklich diese werte,naja...
dann hab ich soweit alles verstanden nur noch nicht
so ganz den teil (5) könntest du mir den nochmal erklären.
wieso die zeitspanne um  größer sein muss? größer sein muss?
und zu der herleitung ,dass gilt :

das verstehe ich auch noch nicht so ganz... 

|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 04. Apr 2009 22:59 Titel: schnudl Verfasst am: 04. Apr 2009 22:59 Titel: |
 |
|
Nimm den direkten Weg - meine ursprüngliche Erklärung ist etwas umständlich:
Die mittlere Geschwindigkeit ist definiert als

Daher ist

Nun haben wir:

und (das haben wir schon diskutiert)
 \cdot \hat v = (2/\pi) \cdot \alpha \sqrt{Lg})
Das ergibt eingesetzt
 \cdot \alpha \sqrt{Lg}} = \pi \cdot \sqrt{L/g})
Nun noch mit 2 multiplizieren, da es ja auch noch eine Rückschwingung gibt.
===
Zur Frage bez. der Näherung für cos:
Hast du denn schon von Taylorreihen gehört? Falls ja, dann wäre es eine gute Übung für dich, dein Mathematikwissen hier anzuwenden, indem du cos(x) für x=0 in eine Taylorreihe entwickelst. 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 05. Apr 2009 13:00 Titel: Ricky Verfasst am: 05. Apr 2009 13:00 Titel: |
 |
|
vielen dank nochmals für deine hilfe.
jetzt habe ich es komplett verstanden. 
nein von taylorreihen habe ich noch nichts gehört.
aber ich werde mich mal mit dem thema vertraut machen.
vielen dank nochmals 
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 26. Mai 2009 16:20 Titel: Ricky Verfasst am: 26. Mai 2009 16:20 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: |
Der Mittelwert einer Funktion im Intervall x1 bis x2 ist
 = \frac{1}{x_2-x_1} \cdot \int_{x_1}^{x_2} y(x) \dd x)
Wir wollen den Mittelwert von
 )
im Intervall

also
 \, \dd \varphi = \frac{\hat v}{\pi} (\sin \varphi )|_{-\pi /2}^{+\pi/2} = 2 \hat v / \pi)
Das ist der einzige Schritt der nicht ganz so elementar ist. |
hallöchen,
ich muss nochmal auf dieses topic zurückgreifen, da ich nun am freitag ein referat zur herleitung dieser formel halten soll.
nun habe ich noch ein paar fragen zu diesem teil der herleitung.
also zunächst. warum benötigt man den mittelwert von  ) und wie kommt man plötzlich von und wie kommt man plötzlich von  auf auf  . .
Und wie kommt man zunächst auf  und dann auf und dann auf 
könntest du mir das bitte nochmal erklären shnudl?
oder auch jemand anderes ,wenn er es versteht?
vielen lieben dank 
|
|
 |
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
 wishmoep Verfasst am: 26. Mai 2009 17:29 Titel: wishmoep Verfasst am: 26. Mai 2009 17:29 Titel: |
 |
|
Ich probiere dir auf die Schnelle zu helfen.
| Ricky hat Folgendes geschrieben: | also zunächst. warum benötigt man den mittelwert von  ) |
Während der ganzen Bewegung ändert sich doch die Geschwindigkeit, du kannst ja nicht einfach die Maximalgeschwindigkeit nehmen, dann könnte man ja auch v=0 nehmen, wenn das Pendel keine kinetische Energie mehr hat.
| Ricky hat Folgendes geschrieben: | und wie kommt man plötzlich von  auf auf  . .
Und wie kommt man zunächst auf  und dann auf und dann auf  |
Du setzt deinen Anfangspunkt am Punkt der höchsten Geschwindigkeit, ergo sollte der Kosinus dein Ausgangspunkt sein, oder eben der Sinus mit einer Phasenverschiebung um pi/2.
) oder oder )
Ferner - Indem du den Mittelwert bildest!.
Hast du die Herleitung des Mitterlwertes verstanden? Du kannst integrieren? Du kennst die Formel für den Mittelwert einer Funktion?
|
|
 |
|



















 )
)