| Autor |
Nachricht |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 07. Apr 2008 21:12 Titel: Fadenpendel felix1992 Verfasst am: 07. Apr 2008 21:12 Titel: Fadenpendel |
 |
|
moin, 2 kurze aufgaben:
1) Warum schwingt ein Fadenpendel nur bei kleinen amplituden harmonisch?
welche energieformen tretten hier auf?
-Energie der Lage; kinetische Energie
Gibt die Gesamtenergie an:
Gesamte Energie= Energie der Lage+ kinetische Energie= konstant
richtig?
2) Zwei Pendel (T1= 1,5s , T2=1,6 s) werden gleich weit ausgelenkt und und gleichzeitig losgelassen. Wann sind sie erstmals gleichphasig?
Wieviele Perioden hat dann jedes Pendel ausgeführt?
mein Ansatz: man muss das kgV bilden und davon die Hälfte also in diesem fall sind sie nach 12 sekunden das erste mal gleichphasig.
Das Pendel 1 hat zu diesem Zeitpunkt 8 schwingungen ausgeführt und das pendel 2 hat zu diesem Zeitpunkt 7,5 schwingungen ausgeführt.
Ist das richtig? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Apr 2008 01:09 Titel: Re: Fadenpendel dermarkus Verfasst am: 08. Apr 2008 01:09 Titel: Re: Fadenpendel |
 |
|
| felix1992 hat Folgendes geschrieben: | man muss das kgV bilden und davon die Hälfte
[...]
also in diesem fall sind sie nach 12 sekunden das erste mal gleichphasig.
Das Pendel 1 hat zu diesem Zeitpunkt 8 schwingungen ausgeführt und das pendel 2 hat zu diesem Zeitpunkt 7,5 schwingungen ausgeführt.
|
Wie kommst du auf diese Bedingung? Magst du dir das am besten einfach mal aufmalen? Sind nach 12 s die beiden Schwingungen nicht gerade gegenphasig?
Wenn du das statt mit Aufmalen lieber mit einer Gleichung lösen magst, dann könntest du ansetzen, zu welchen Zeitpunkten  die Phase der einen Schwingung mit der Phase der anderen Schwingung bis auf Summanden von ganzzahligen Vielfachen von die Phase der einen Schwingung mit der Phase der anderen Schwingung bis auf Summanden von ganzzahligen Vielfachen von 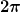 übereinstimmt. übereinstimmt. |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 08. Apr 2008 08:40 Titel: felix1992 Verfasst am: 08. Apr 2008 08:40 Titel: |
 |
|
aeh ja du hast recht nach 12 sekunden sie gegenphasig...sry.
ich habe es durchs probieren rausbekommen.. |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 09. Apr 2008 14:51 Titel: felix1992 Verfasst am: 09. Apr 2008 14:51 Titel: |
 |
|
und?
gruß |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Apr 2008 15:07 Titel: dermarkus Verfasst am: 09. Apr 2008 15:07 Titel: |
 |
|
|
Wie weit kommst du, wenn du das mit dem, was du nun weißt, nochmal probierst? Also, wie oben schon gesagt, durch Probieren und Aufmalen oder mit einer Gleichung? |
|
 |
Dr. Mechanikus
Anmeldungsdatum: 07.04.2008
Beiträge: 19
|
 Dr. Mechanikus Verfasst am: 09. Apr 2008 15:33 Titel: Dr. Mechanikus Verfasst am: 09. Apr 2008 15:33 Titel: |
 |
|
Wenn du die Summe aller Momente um den Aufhängepunkt berechnest, erhälst du die folgende DGL für den Winkel:
=0)
Dies ist eine nichtlineare Differentialgleichung. Bei kleinen Schwingungen, kann man näherungsweise setzen:
\approx\varphi)
und du erhälst eine gewöhnliche Differentialgleichung 2. Ordnung:

Die Lösung hierfür ist die Gleichung einer harmonischen Schwingung. Bei großen Winkeln musst du die nichtlineare DGL lösen, was auf eine nichtharmonische Schwingung führt.
Die auftretenden Energien sind nur die kinetische und die potentielle
^2+mgl(1-cos(\varphi))) |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 09. Apr 2008 15:47 Titel: felix1992 Verfasst am: 09. Apr 2008 15:47 Titel: |
 |
|
| Dr. Mechanikus hat Folgendes geschrieben: | Wenn du die Summe aller Momente um den Aufhängepunkt berechnest, erhälst du die folgende DGL für den Winkel:
=0)
Dies ist eine nichtlineare Differentialgleichung. Bei kleinen Schwingungen, kann man näherungsweise setzen:
\approx\varphi)
und du erhälst eine gewöhnliche Differentialgleichung 2. Ordnung:

Die Lösung hierfür ist die Gleichung einer harmonischen Schwingung. Bei großen Winkeln musst du die nichtlineare DGL lösen, was auf eine nichtharmonische Schwingung führt.
Die auftretenden Energien sind nur die kinetische und die potentielle
^2+mgl(1-cos(\varphi))) |
ja das verstehe ich schon mal komplett nicht:D kannst es mir bissel auf schulnivou erklären?
zu aufgabe 2:
was meinen die mit gleichphasig? den zeitpunkt wo sie die t-achse am gleichen punkt kreuzen? das wäre ja dann nach 12 sekunden? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 09. Apr 2008 15:52 Titel: felix1992 Verfasst am: 09. Apr 2008 15:52 Titel: |
 |
|
wenn ich mir das bei azufgabe 2 nochmal rechnerisch durch kopf gehen lasse kann ich dann nicht s(t)= A*sin((2 phi/1,5s)*t) mit der gleichung
s(t)=A*sin((2Phi/1.6 s)*t) gleichsetzen? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Apr 2008 16:33 Titel: dermarkus Verfasst am: 09. Apr 2008 16:33 Titel: |
 |
|
| felix1992 hat Folgendes geschrieben: | wenn ich mir das bei azufgabe 2 nochmal rechnerisch durch kopf gehen lasse kann ich dann nicht s(t)= A*sin((2 phi/1,5s)*t) mit der gleichung
s(t)=A*sin((2Phi/1.6 s)*t) gleichsetzen? |
Ja, damit bist du schon auf der richtigen Spur  Nun musst du nur noch berücksichtigen, dass man eine Phase ja auch dann als gleich bezeichnen möchte, wenn man zu ihr ein ganzzahliges Vielfaches von Nun musst du nur noch berücksichtigen, dass man eine Phase ja auch dann als gleich bezeichnen möchte, wenn man zu ihr ein ganzzahliges Vielfaches von 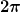 dazuaddiert. dazuaddiert.
Und außerdem möchtest du genaugenommen nicht die Auslenkungen s(t) gleichsetzen (es ist ja hier nicht nach "gleichauslenkig" oder so gefragt  ), sondern die Phasen, also das, was jeweils in der Klammer hinter dem Sinus steht. (Denn es gibt Punkte, an denen zwar die Auslenkung der beiden Schwingungen gleich ist, nicht aber ihre Phase. Einem davon bist du oben schon begegnet, das ist der nach 12 s.) ), sondern die Phasen, also das, was jeweils in der Klammer hinter dem Sinus steht. (Denn es gibt Punkte, an denen zwar die Auslenkung der beiden Schwingungen gleich ist, nicht aber ihre Phase. Einem davon bist du oben schon begegnet, das ist der nach 12 s.) |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 09. Apr 2008 17:45 Titel: felix1992 Verfasst am: 09. Apr 2008 17:45 Titel: |
 |
|
hm also? s(t)= A*sin((2 phi/1,5s)*t+phi) mit der gleichung
s(t)=A*sin((2Phi/1.6 s)*t+phi) gleichsetzen?
oder wie berücksichtige ich die phase? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Apr 2008 13:09 Titel: dermarkus Verfasst am: 10. Apr 2008 13:09 Titel: |
 |
|
Hm, da verstehe ich deine Überlegung dahinter nicht so recht, für mich wirkt das mit deinen Formeln bisher noch mehr geraten als überlegt.
(Meinst du in deinen Formeln übrigens phi ( ) oder pi ( ) oder pi (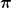 ) ?) ) ?)
Ich würde vorschlagen, du überlegst und löst dir das ganze am besten erst mal rein zeichnerisch, und versuchst erst einmal durch Aufmalen der beiden Funktionen herauszufinden, wann beide Schwingungen zum ersten Mal wieder gleichphasig sind. |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 10. Apr 2008 15:05 Titel: felix1992 Verfasst am: 10. Apr 2008 15:05 Titel: |
 |
|
|
eien verständnisfrage: gleichphasig bedeutet doch wann sie sich das erste mal kreuzen oder? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Apr 2008 15:13 Titel: dermarkus Verfasst am: 10. Apr 2008 15:13 Titel: |
 |
|
|
Nein, das wäre ein Punkt, indem sie beide dieselbe Auslenkung haben. Aber hier in dieser Aufgabe ist ja nicht nach dem Kriterium "gleiche Auslenkung", sondern nach "gleiche Phase" gefragt. |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 10. Apr 2008 15:22 Titel: felix1992 Verfasst am: 10. Apr 2008 15:22 Titel: |
 |
|
|
das heißt wenn sie zusammen die x-achse schneiden? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Apr 2008 15:24 Titel: dermarkus Verfasst am: 10. Apr 2008 15:24 Titel: |
 |
|
Nein. Schau dir nochmal die Grundlagen an:
Wenn du ein
=A\cdot \sin(\varphi(x,t)))
siehst, was ist denn dabei die Auslenkung, was die Amplitude und was die Phase der Schwingung? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 10. Apr 2008 16:00 Titel: felix1992 Verfasst am: 10. Apr 2008 16:00 Titel: |
 |
|
s(t)=A*sin((2w*t)+phi)
s(t)=A*sin((w*t)+phi)
ist das richtig? die wellen haben beide verschiedene frequenzen aber sind beide gleichphasig?
bei dir ist s(t) die auslenktung zum zeitpunkt t
A ist die amplitude und phi die phase.. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Apr 2008 17:58 Titel: dermarkus Verfasst am: 10. Apr 2008 17:58 Titel: |
 |
|
| Zitat: |
bei dir ist s(t) die auslenktung zum zeitpunkt t
A ist die amplitude und phi die phase.. |
Einverstanden. Denn das phi in meiner Gleichung ist alles das, was in den Klammern hinter dem Sinus steht.
| felix1992 hat Folgendes geschrieben: | s(t)=A*sin((2w*t)+phi)
s(t)=A*sin((w*t)+phi)
ist das richtig?
|
Nein, da verwechselst du noch etwas: Was du hier mit phi bezeichnet hast, ist nicht die Phase der Schwingung, sondern die Nullphase.
Die Nullphase ist ein konstanter Wert, nämlich die Phase der Schwingung zum Zeitpunkt Null. |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 10. Apr 2008 19:08 Titel: felix1992 Verfasst am: 10. Apr 2008 19:08 Titel: |
 |
|
ahso und wie baue ich die phase ein?
da leigt wahrscheinlich mein denkproblem... |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Apr 2008 19:15 Titel: dermarkus Verfasst am: 10. Apr 2008 19:15 Titel: |
 |
|
Versuch mal das genau zu lesen und anzuwenden, was ich dir oben erzählt habe und was sicher auch in deinen Aufschrieben und deinem Physikbuch steht:
Was ist denn die Phase der Schwingung s(t), wenn die Schwingung so lautet:
 = A\cdot \sin(\omega t)) |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 10. Apr 2008 20:08 Titel: felix1992 Verfasst am: 10. Apr 2008 20:08 Titel: |
 |
|
|
wt? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Apr 2008 20:46 Titel: dermarkus Verfasst am: 10. Apr 2008 20:46 Titel: |
 |
|
Genau  Denn das ist das, was in der Klammer hinter dem Sinus steht. Denn das ist das, was in der Klammer hinter dem Sinus steht.
Wie lauten denn dann die Phasen der beiden Schwingungen in der Aufgabe 2 aus deinem ersten Beitrag? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 10. Apr 2008 21:42 Titel: felix1992 Verfasst am: 10. Apr 2008 21:42 Titel: |
 |
|
s(t)=A* sin(2pi/1.5 s*t)
s(t) =A*sin(2Pi/1.6 s*t)
??ß
also wenn es bedeuetet den nullphasenwinkel zu nennen dann kann man schreiben s(t)=A*sin(2pi/T*t +phi)
aber in welche phase dann ist die gesamte klammer hinter dem sinus gemeint? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Apr 2008 23:02 Titel: dermarkus Verfasst am: 10. Apr 2008 23:02 Titel: |
 |
|
|
Nein, ich meine nicht die Auslenkungen , nicht die Amplituden, nicht die Nullphasenwinkel, einfach nur die Phasen. |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 11. Apr 2008 09:05 Titel: felix1992 Verfasst am: 11. Apr 2008 09:05 Titel: |
 |
|
hae die phase ist das was in der klammer steht...
beide schwingungen sind gleich bis auf die periode T?---
was mach ich den falsch? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Apr 2008 13:21 Titel: dermarkus Verfasst am: 11. Apr 2008 13:21 Titel: |
 |
|
| felix1992 hat Folgendes geschrieben: | hae die phase ist das was in der klammer steht...
beide schwingungen sind gleich bis auf die periode T?---
|
Ja 
Schreib also mal nur die Phase der einen Schwingung hin, und darunter nur die Phase der anderen Schwingung.
Phase der einen Schwingung = ???
Phase der anderen Schwingung = ??? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 11. Apr 2008 14:33 Titel: felix1992 Verfasst am: 11. Apr 2008 14:33 Titel: |
 |
|
(2pi/1,5s *t)
(2pi/1,6s *t)
richtig>? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Apr 2008 14:58 Titel: dermarkus Verfasst am: 11. Apr 2008 14:58 Titel: |
 |
|
Richtig 
Nun zwei Aufgaben:
1.) Es gibt einen einzigen Zeitpunkt, zu dem diese beiden Phasen ganz genau gleich sind. Welcher Zeitpunkt ist das?
2.) Es gibt Zeitpunkte, an denen sich diese beiden Phasen genau um ein ganzzahliges Vielfaches von 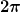 unterscheiden. Welche Zeitpunkte sind das? unterscheiden. Welche Zeitpunkte sind das? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 11. Apr 2008 15:54 Titel: felix1992 Verfasst am: 11. Apr 2008 15:54 Titel: |
 |
|
|
die bekomme ich raus indem ich sie einfach gleichsetzte also die beidne phasen? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Apr 2008 18:43 Titel: dermarkus Verfasst am: 11. Apr 2008 18:43 Titel: |
 |
|
Die 1.) : Ja  |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 11. Apr 2008 20:18 Titel: felix1992 Verfasst am: 11. Apr 2008 20:18 Titel: |
 |
|
keine ahnung bitte helf mir.. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Apr 2008 20:22 Titel: dermarkus Verfasst am: 11. Apr 2008 20:22 Titel: |
 |
|
|
Wo ist das Problem? Magst du einfach mal das machen, was du gesagt hast, um die Frage 1.) zu beantworten? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 11. Apr 2008 20:34 Titel: felix1992 Verfasst am: 11. Apr 2008 20:34 Titel: |
 |
|
hae wenn ich 2*3,14/1,5s*t=2*3,14/ 1,6s *t
dann kriege ich:
4,19t= 3,93t
und dann?
oder muss ich die gsamte fomel gleichsetzen?
s(t)=s(t) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Apr 2008 20:39 Titel: dermarkus Verfasst am: 11. Apr 2008 20:39 Titel: |
 |
|
| felix1992 hat Folgendes geschrieben: | hae wenn ich 2*3,14/1,5s*t=2*3,14/ 1,6s *t
dann kriege ich:
4,19t= 3,93t
und dann?
|
Genau  Und welche Lösung für t bekommst du dann aus dieser Gleichung? Und welche Lösung für t bekommst du dann aus dieser Gleichung? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 11. Apr 2008 20:41 Titel: felix1992 Verfasst am: 11. Apr 2008 20:41 Titel: |
 |
|
|
wie mache ich das weiter? weil wenn ich durch t teile gehts nicht ... |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Apr 2008 20:46 Titel: dermarkus Verfasst am: 11. Apr 2008 20:46 Titel: |
 |
|
Welches ist der einzige Wert für t , für den diese Gleichung erfüllt ist? Siehst du den direkt?
Oder magst du vielleicht zuerst noch auf beiden Seiten der Gleichung das subtrahieren, was rechts vom Gleichheitszeichen steht, und dann noch durch den Vorfaktor vor dem t teilen? Was steht dann als Lösung da?
Ergibt diese Lösung dann für dich einen Sinn, hättest du diese Lösung erwartet? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 11. Apr 2008 20:47 Titel: felix1992 Verfasst am: 11. Apr 2008 20:47 Titel: |
 |
|
die lösung ergeben für mich einen sinn aber ich haette sie neimals erwartet.
das heißt sie sind nur zu dem zeitpunkt o gleichphasig sonst nie? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Apr 2008 20:52 Titel: dermarkus Verfasst am: 11. Apr 2008 20:52 Titel: |
 |
|
Wenn die beiden Phasen ganz genau gleich sein sollen, ja. (Und dass die beiden Schwingungen am Anfang, also zum Zeitpunkt t=0 gleichphasig sind, das haben wir ja schon gewusst, denn so werden die Schwingungen ja gestartet.)
Aber nun kommen wir zu meiner Frage 2.)
Denn man sagt ja auch dann noch, dass zwei Schwingungen gleichphasig sind, wenn ihren Phasen bis auf ganzzahlige Vielfache von 2 pi gleich sind. Denn nach einer Periodendauer, das heißt nach einer Phase von 2 pi, wiederholt sich eine Schwingung ja.
Was bekommst du, wenn du nun anfängst, die Frage 2.) zu lösen? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 12. Apr 2008 09:09 Titel: felix1992 Verfasst am: 12. Apr 2008 09:09 Titel: |
 |
|
ich habe keine ahnung vom lösungsansatz...
muss ja was mitm gangunterscheid sein oder? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 12. Apr 2008 10:44 Titel: dermarkus Verfasst am: 12. Apr 2008 10:44 Titel: |
 |
|
Den Lösungsansatz habe ich dir in Worten ja schon komplett gesagt:
Die eine Phase plus ein ganzzahliges Vielfaches von 2 pi soll gleich der anderen Phase sein.
Kannst du das als Gleichung hinschreiben und aus dieser Gleichung bestimmen, für welche t sie erfüllt ist? |
|
 |
felix1992
Anmeldungsdatum: 28.10.2007
Beiträge: 76
|
 felix1992 Verfasst am: 12. Apr 2008 11:02 Titel: felix1992 Verfasst am: 12. Apr 2008 11:02 Titel: |
 |
|
4,19t= 3,93t+6,28
0,26t=6,28
t=24,15 also ungefähr 24,2 sekunden
ist das richtig? also die lösung für meine aufgabe ist deine aufgabe 2? |
|
 |
|
















 Nun musst du nur noch berücksichtigen, dass man eine Phase ja auch dann als gleich bezeichnen möchte, wenn man zu ihr ein ganzzahliges Vielfaches von
Nun musst du nur noch berücksichtigen, dass man eine Phase ja auch dann als gleich bezeichnen möchte, wenn man zu ihr ein ganzzahliges Vielfaches von  ), sondern die Phasen, also das, was jeweils in der Klammer hinter dem Sinus steht. (Denn es gibt Punkte, an denen zwar die Auslenkung der beiden Schwingungen gleich ist, nicht aber ihre Phase. Einem davon bist du oben schon begegnet, das ist der nach 12 s.)
), sondern die Phasen, also das, was jeweils in der Klammer hinter dem Sinus steht. (Denn es gibt Punkte, an denen zwar die Auslenkung der beiden Schwingungen gleich ist, nicht aber ihre Phase. Einem davon bist du oben schon begegnet, das ist der nach 12 s.)