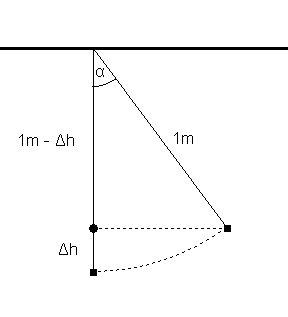
Fadenpendel - Geschwindigkeit

_Alex_ · Anmeldungsdatum: 17.09.2006 Beiträge: 154

Hallo,

folgende Aufgabe::: Ein Fadenpendel hängt an einem 1,0m langen Faden und wird 30° ausgelenkt. Berechnen Sie:

a.) die maximale Geschwindigkeit beim schwingen (ohne reibung)

b.)wie groß die Geschwindigkeit wäre, wenn beim schwingen ( ohne reibung) mech. Energie verloren gegangen wäre.

bei a.) könnte ich noch die beiden übrigen seiten des dreiecks berechnen. Aber ob das was bringt?

Aufjeden fall komm ich nicht weiter...
hilfe ist erforderlich

dankeschön

eman · Anmeldungsdatum: 24.06.2006 Beiträge: 59

Mit deinem Dreieck kannst du die Höhe h des Schwerpunkts (bei 30°)
als Abstand über dem tiefsten Ort (bei 0°) berechnen.

Der Energievergleich m*g*h = m*v^2/2 liefert dann die Geschwindigkeit.

Geht Energie 'verloren', dann ist die Geschwindigkeit geringer.

_Alex_ · Anmeldungsdatum: 17.09.2006 Beiträge: 154

also ich habe jetzt a die längere diagonale seite berrechnet berrechnet mit a=1,154 und b die waagerechte seite mit b=0,577 jetzt habe ich deltah berechnet mit a-1 also 1,154-1 das macht 0,154 dann halt den energiesatz umgestellt nach v d.h. v=Wurzel aus 2*g*h

und das ergibt bei mir 1,742 m/s in der Lösung steht aber 1,62 m/s was habe ich also falsch gemacht?

para · Moderator Anmeldungsdatum: 02.10.2004 Beiträge: 2874 Wohnort: Dresden

_Alex_ · Anmeldungsdatum: 17.09.2006 Beiträge: 154

http://www.bilder-hochladen.net/files/1gj4-1.jpg

so meine ich das...[/img]

para · Moderator Anmeldungsdatum: 02.10.2004 Beiträge: 2874 Wohnort: Dresden

Denkst du nicht, dass a die Fadenlänge ist, und daher konstant bleiben sollte? Kannst du mit der angehängten Skizze vielleicht etwas anfangen, und dort einen Ausdruck für die Höhendifferenz herleiten?

_Alex_ · Anmeldungsdatum: 17.09.2006 Beiträge: 154

OK jetzt ist es einfach, danke für die Skizze!

ich sag mal das 1m-delta h = l

d.h. cos (alpha)=l / 1m

l=0,866m

delta h =1m-0,866m

delta h=0,13397

Epot=Ekin

m*g*h=0,5m*v²

umstellen nach v: v=Wurzel aus 2*g*h

v=1,62 m/s :-)

_Alex_ · Anmeldungsdatum: 17.09.2006 Beiträge: 154

aber b.)... wie soll das mit den 5% funktionieren?

man muss doch da irgendwie 5/100 oder 0,05 von der mech. energie abziehen. aber wie?

eman · Anmeldungsdatum: 24.06.2006 Beiträge: 59

Wenn unten 5% der anfänglichen Energie fehlen dann ist v^2 = 0,95 * 2*g*h und v = 1,58 m/s.