| Autor |
Nachricht |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 17. Nov 2008 17:25 Titel: Herleitung Raketengleichung / Beschleunigung einer Rakete Superhirn Verfasst am: 17. Nov 2008 17:25 Titel: Herleitung Raketengleichung / Beschleunigung einer Rakete |
 |
|
Hallo,
wir haben neulich an der Uni eine Aufgabe zur Rakete bekommen. Dabei sollten wir die Raketengleichung (=v(t)) herleiten, ohne Gravitationswirkung allerdings.
Mit dem Ansatz m*a=-R*v (=F Schub) hab ich dazu die DGL aufgestellt und gelöst. Wir sollten das mit einfachem Integrieren auf beiden Seiten machen. Jetzt ist nur die Frage wieso man da das bestimmte Integral von 0 bis t benutzt? Klar, wenn man keine Bedingungen hat, kann man beim unbest. Integral auch nicht die Integrationskonstante c bestimmen, aber wieso von 0 bis t integrieren? Wird das immer so gemacht bei fehlenden Bedingungen?
So und noch eine Frage zum Schluss: Raus kam dann die bekannte Raketengleichung, als Graph halt eine ln Funktion. Davon die ABleitung ist ja eine Art Hyperbel, also gleich die Beschleunigung. Demnach müsste ja eigentlich die Beschleunigung mit zunehmender Zeit auch kleiner werden. Doch wird die doch größer, da die Rakete immer mehr Masse pro Zeit verliert und FSchub immer größer wird (-R*v) ->F=m*a
WIe kann das sein?
Gruss Superhirn
|
|
 |
Herbststurm

Anmeldungsdatum: 05.09.2008
Beiträge: 412
Wohnort: Freiburg i. Brsg.
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 18. Nov 2008 12:50 Titel: Superhirn Verfasst am: 18. Nov 2008 12:50 Titel: |
 |
|
Ich hoffe ich habs richtig verstanden:
Also wenn man nicht von t_anfang bis t_ende integrieren würde, dann würde man bei der Herleitung der Formel von einem beliebigen Zeitpunkt t_start (wo die Geschwindigkeit nicht null ist, die Rakete also schon gestartet ist) bis zum Ende t_ende die Anfangsgeschwindigkeit vernachlässigen?
Doch da wird nicht erklärt wo man sowas anwendet. Wir hatten nämlich schon DGL's wo das nicht gemacht wurde, sondern einfach die Stammfunktion gebildet wurde.
Und über die Beschleunigung steht da irgendwie garnichts? Nur die Formel bei der Herleitung eben, aber die hilft mir auch nix, denn wenn ich die plotten lasse wird das eher ne Gerade mit ganz kleiner Steigung.
Gruss Superhirn
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Nov 2008 17:39 Titel: Re: Herleitung Raketengleichung / Beschleunigung einer Raket dermarkus Verfasst am: 18. Nov 2008 17:39 Titel: Re: Herleitung Raketengleichung / Beschleunigung einer Raket |
 |
|
| Superhirn hat Folgendes geschrieben: | Jetzt ist nur die Frage wieso man da das bestimmte Integral von 0 bis t benutzt?
|
Vielleicht schaust du dir das mal so an:
Was soll die Bedeutung der Variablen t in der Gleichung sein, die du dann am Ende herausbekommst? Wenn das die Zeit bezeichnen soll, die seit Anfang der Raketenbewegung verstrichen ist, dann entspricht das ja genau dieser Wahl der Integrationsgrenzen 
| Zitat: |
So und noch eine Frage zum Schluss: Raus kam dann die bekannte Raketengleichung, als Graph halt eine ln Funktion. Davon die ABleitung ist ja eine Art Hyperbel, also gleich die Beschleunigung. Demnach müsste ja eigentlich die Beschleunigung mit zunehmender Zeit auch kleiner werden.
|
Magst du mal die zugehörigen Gleichungen konkret hier aufschreiben? Wie lautet deine Bewegungsgleichung, dein v(t) , dein a(t) ? Wie bist du auf die ln-Funktion gekommen?
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 18. Nov 2008 23:35 Titel: Superhirn Verfasst am: 18. Nov 2008 23:35 Titel: |
 |
|
| Zitat: | | Was soll die Bedeutung der Variablen t in der Gleichung sein, die du dann am Ende herausbekommst? Wenn das die Zeit bezeichnen soll, die seit Anfang der Raketenbewegung verstrichen ist, dann entspricht das ja genau dieser Wahl der Integrationsgrenzen |
Hmm ok, macht schon Sinn so mit dem 0 und t. Benutzt man das nur bei der Raketengleichung oder auch irgwendwo anders? Bisher hab ichs nämlich bei DGL's von dem Typ immer so gesehen, dass man die Stammfkt allgemein gebildet hat und dann durch Nebenbedingungen die Integrationskonstante ermittelt hat.
| Zitat: | | Magst du mal die zugehörigen Gleichungen konkret hier aufschreiben? Wie lautet deine Bewegungsgleichung, dein v(t) , dein a(t) ? Wie bist du auf die ln-Funktion gekommen? |
Ansatz: 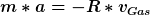
Die Gleichung für die Geschwindikeit hab ich eben durch Lösung der DGL bekommen:
=v_{Gas}*ln(\frac{m_{0}}{m_{0}-R*t})) ... Geschwindigkeit ... Geschwindigkeit
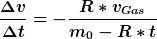 ... DGL ... DGL
Die Ableitung der Geschwindigkeitsfunktion ist ja dann die Beschleunigung, bzw die DGL wieder selber. Die wird ja immer größer, sieht man ja auch an der Formel, wenn man sich das Verhalten für größer werdendes t anschaut. Die Stammfunktion ist doch aber eine ln Funktion, die doch eine Art Sättigungskurve beschreibt. Die rein grafische Ableitung davon müsste doch so ne Art Hyperbel sein. Da kann was nicht stimmen
Gruss Superhirn
Zuletzt bearbeitet von Superhirn am 18. Nov 2008 23:46, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Nov 2008 23:45 Titel: dermarkus Verfasst am: 18. Nov 2008 23:45 Titel: |
 |
|
| Superhirn hat Folgendes geschrieben: | Benutzt man das nur bei der Raketengleichung oder auch irgwendwo anders?
|
a, wenn man Lust hat oder die Aufgabenstellung das mal erfordert, kann man sicher jederzeit auch irgendeinen Teilabschnitt von 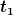 bis bis 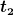 betrachten. betrachten.
| Zitat: |
Da kann was nicht stimmen
|
Einverstanden.
Wie genau hast du deine Differentialgleichung aufgestellt, und was bedeuten die Buchstaben darin?
Magst du mal überprüfen, ob du nicht zum Beispiel die konstant bleibende Ausströmgeschwindigkeit des ausgestoßenen Gases mit der Geschwindigkeit v(t) der Rakete verwechselt hast?
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 18. Nov 2008 23:57 Titel: Superhirn Verfasst am: 18. Nov 2008 23:57 Titel: |
 |
|
| Zitat: | a, wenn man Lust hat oder die Aufgabenstellung das mal erfordert, kann man sicher jederzeit auch irgendeinen Teilabschnitt von bis betrachten.
|
Ok, gut zu wissen.
| Zitat: | | Wie genau hast du deine Differentialgleichung aufgestellt, und was bedeuten die Buchstaben darin? |
Durch den oben genannten Ansatz habe ich m durch 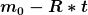 ersetzt und auf die andere Seite gebracht. Das liefert auch schon die DGL. Diese eben von 0 bis t integriert liefert die Raketengleichung. Wüsste jetzt eigentlich nicht, wo ich ersetzt und auf die andere Seite gebracht. Das liefert auch schon die DGL. Diese eben von 0 bis t integriert liefert die Raketengleichung. Wüsste jetzt eigentlich nicht, wo ich 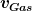 mit v verwechselt hätte. mit v verwechselt hätte.
Gruss Superhirn
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 00:14 Titel: dermarkus Verfasst am: 19. Nov 2008 00:14 Titel: |
 |
|
Danke fürs Nachtragen deiner Ausgangsgleichung und nähere Beschreiben deines Rechenweges 
Mit deiner Rechnung bin ich einverstanden 
Magst du dir dein Ergebnis mal auftragen und sehen: In welche Richtung auf der Hyperbel für die Beschleunigung der Rakete geht man für wachsende Zeiten t?
(Und welches Vorzeichen hat die Gasgeschwindigkeit 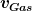 , wenn die Beschleunigung eine positive Größe sein soll?) , wenn die Beschleunigung eine positive Größe sein soll?)
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 19. Nov 2008 00:46 Titel: Superhirn Verfasst am: 19. Nov 2008 00:46 Titel: |
 |
|
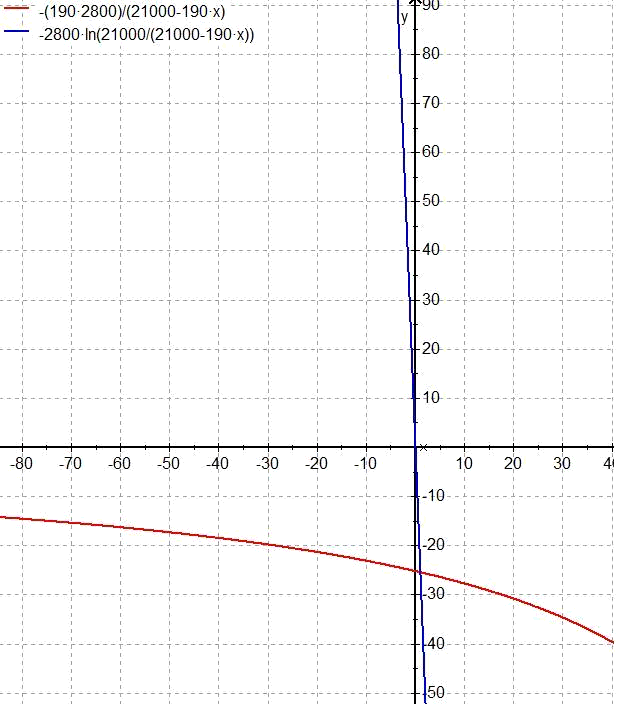
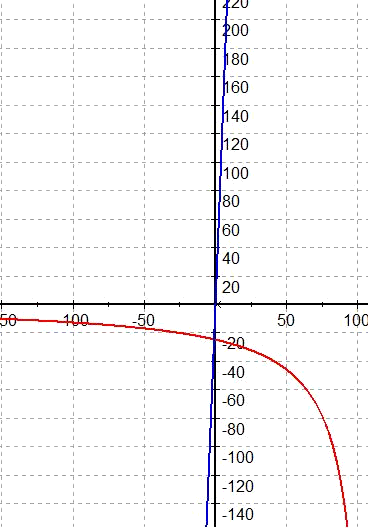
So, hab mir die beiden Graphen mal gezeichnet:
Die Beschleunigung geht in den negativen Bereich und wird für größeres t immer größer. Macht Sinn.
Die Geschwindigkeitskruve steigt recht steil an und eine Sättigung ist für positive x-Wert nicht zu sehen. Sättigung gibts nur wenn man sich den negativen Bereich der x-Achse anschaut. Die Geschwindigkeit muss doch denselben Vektor wie die Beschleunigung haben oder?
Wenn man das Vorzeichen von v_Gas in der v(t) Funktion ändert, steigt die Geschwindigkeit schonmal in dieselbe Richtung an, wie die Beschleunigung, aber Sättigung gibts i-wie immer noch keine.
Gruss Superhirn
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 00:59 Titel: dermarkus Verfasst am: 19. Nov 2008 00:59 Titel: |
 |
|
Da kann ich noch nicht so ganz erraten, was du da in deinen Graphen anschaust.
Hast du zum Beispiel darauf geachtet, nur den physikalisch sinnvollen Teil deiner Graphen zu betrachten, also bei t=0 zu starten und in Richtung zu positiven Zeiten zu gehen?
Und wie musst du das Vorzeichen des Wertes der Größe 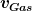 wählen, damit sowohl v(t) als auch a(t) der Rakete positiv sind? wählen, damit sowohl v(t) als auch a(t) der Rakete positiv sind?
Zeige gerne deine Graphen mal hier, denn ich vermute, das macht es viel leichter, zu sagen und zu verstehen, was du ihnen ansiehst.
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 11:18 Titel: dermarkus Verfasst am: 19. Nov 2008 11:18 Titel: |
 |
|
Das ) sollte die Steigung von sollte die Steigung von ) sein; das ist es aber, so wie deine Diagramme es deutlich zeigen, überhaupt noch nicht. sein; das ist es aber, so wie deine Diagramme es deutlich zeigen, überhaupt noch nicht.
Mit deinem ) bin ich bereits einverstanden, aber magst du nochmal die Stammfunktion für bin ich bereits einverstanden, aber magst du nochmal die Stammfunktion für ) überprüfen, die du da hingeschrieben hast, ob die beim Ableiten auch wieder das überprüfen, die du da hingeschrieben hast, ob die beim Ableiten auch wieder das ) ergibt? ergibt?
(Beachte zum Beispiel: Die Stammfunktion von 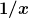 ist ist ) , also steht das , also steht das  im im 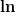 ganz normal "im Zähler", während es in der Ableitung im Nenner steht. In deiner Stammfunktion scheinst du hingegen das ganz normal "im Zähler", während es in der Ableitung im Nenner steht. In deiner Stammfunktion scheinst du hingegen das  im im 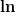 im Nenner gelassen zu haben. ) im Nenner gelassen zu haben. )
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 19. Nov 2008 21:05 Titel: Superhirn Verfasst am: 19. Nov 2008 21:05 Titel: |
 |
|
Also:
Integration auf beiden Seiten:
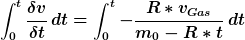
 = -v_{Gas}* [ln(m_{0}-R*t)]^{t}_{0})
 - ln(m_{0})))
)
)
Zur Probe hab ich die beiden letzten Funktionen mal zeichnen lassen und sie sind wirklich identisch!
Deswegen müssen die Formeln eigentlich stimmen. Nur so rein graphisch passt das i-wie überhaupt nicht.
|
|
 |
Zepto
Anmeldungsdatum: 03.10.2007
Beiträge: 323
|
 Zepto Verfasst am: 19. Nov 2008 21:40 Titel: Zepto Verfasst am: 19. Nov 2008 21:40 Titel: |
 |
|
Ich steck jetzt zwar nicht in deiner Rechnung drin, aber beim Integrieren hast du einen Vorzeichenfehler.
Die innere Ableitung ist -R.
Vielleicht hilft das ja.
Gruß
Zepto
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 21:54 Titel: dermarkus Verfasst am: 19. Nov 2008 21:54 Titel: |
 |
|
| Superhirn hat Folgendes geschrieben: |
 - ln(m_{0})))
)
|
Magst du auch diesen Umformschritt nochmal überprüfen?
Und kannst du also nach Korrektur dieser beiden Fehler mit Sicherheit sagen: Welche Version für das Ergebnis von v(t) ist nun die korrekte, die aus deinem neuesten Beitrag oder die vom Anfang des Threads?
Zuletzt bearbeitet von dermarkus am 19. Nov 2008 22:07, insgesamt einmal bearbeitet |
|
 |
Zepto
Anmeldungsdatum: 03.10.2007
Beiträge: 323
|
 Zepto Verfasst am: 19. Nov 2008 22:04 Titel: Zepto Verfasst am: 19. Nov 2008 22:04 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | | Superhirn hat Folgendes geschrieben: |
 - ln(m_{0})))
)
|
Magst du auch diesen Umformschritt nochmal überprüfen? |
Hmm, witzig. Irgendwie fehlert er seinen alten Fehler wieder zurück. 
Kann das sein?
Wenn der Graph nicht passt, muss ja noch irgendwo etwas anderes falsch sein, oder?
Gruß
Zepto
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 22:09 Titel: dermarkus Verfasst am: 19. Nov 2008 22:09 Titel: |
 |
|
Stimmt, die beiden Vorzeichenfehler heben sich gegenseitig raus.
Die oben gezeigten Grafen waren noch für das alte Ergebnis von ganz oben mit dem v(t) mit dem entgegengesetzten Vorzeichen.
Dass jetzt noch etwas an dem Ergebnis falsch sei, habe ich nicht behauptet 
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 19. Nov 2008 22:33 Titel: Superhirn Verfasst am: 19. Nov 2008 22:33 Titel: |
 |
|
Oh, ja ich merke es gerade...
Die beiden Inhalte im ln müssen natürliche bei den letzten beiden formeln vertauscht werden, sry.
 = v_{Gas} * ln(\frac{m_{0}}{m_{0}-R*t}) )
wäre dann die richtige Lösung. Mein letzter Graph zeichnet auch diese Lösung ab. Mir ist der Fehler nur beim texen passiert.
Da der Graph dann aber stimmt gibt das i-wie dann keinen Sinn, denn a geht ins Negative, während v(t) ins Positive geht und keine Sättigung erfährt.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 22:56 Titel: dermarkus Verfasst am: 19. Nov 2008 22:56 Titel: |
 |
|
|
Vorsicht, da hast du bisher nur einen der beiden Fehler korrigiert, die wir beiden gerade angemerkt haben.
|
|
 |
Zepto
Anmeldungsdatum: 03.10.2007
Beiträge: 323
|
 Zepto Verfasst am: 19. Nov 2008 22:56 Titel: Zepto Verfasst am: 19. Nov 2008 22:56 Titel: |
 |
|
| Superhirn hat Folgendes geschrieben: |
 = v_{Gas} * ln(\frac{m_{0}}{m_{0}-R*t}) )
wäre dann die richtige Lösung. |
Hmm, ne! 
Das Logarithmengesetz, das du brauchst lautet:
 = \ln(x) - \ln(y) )
Gruß
Zepto
Edit:Fast gleichzeitig! 
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 19. Nov 2008 23:10 Titel: Superhirn Verfasst am: 19. Nov 2008 23:10 Titel: |
 |
|
Öhm, hab ich doch benutzt, oder? Sorry, ich sehe es wirklich nicht 
Also nochmal ausführlich:
Bis hier seid ihr mir doch einverstanden:
 = -v_{Gas}* (ln(m_{0}-R*t) - ln(m_{0})))
Dann folgt:
 = -v_{Gas}* ln(\frac{m_{0}-R*t}{m_{0}}))
Daraus folgt:
 = v_{Gas}* ln(\frac{m_{0}}{m_{0}-R*t}))
Die Gleichung steht auch in jedem Buch, müsste also stimmen
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 23:20 Titel: dermarkus Verfasst am: 19. Nov 2008 23:20 Titel: |
 |
|
Die Rechnung in den Zeilen, die du da angibst, ist nun okay.
Davor steckt aber noch der zweite Vorzeichenfehler, den Zepto angesprochen hat:
| Superhirn hat Folgendes geschrieben: |
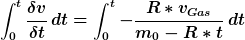
 = -v_{Gas}* [ln(m_{0}-R*t)]^{t}_{0})
|
Zwischen diesen beiden Zeilen hast du noch einen Vorzeichenfehler gemacht.
| Superhirn hat Folgendes geschrieben: |
Die Gleichung steht auch in jedem Buch, müsste also stimmen |
Diese Gleichung stimmt hier nicht, da du in dem Ansatz für deine Rechnung das Vorzeichen von 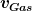 andersherum gewählt hast als "jedes Buch". andersherum gewählt hast als "jedes Buch".
Zuletzt bearbeitet von dermarkus am 19. Nov 2008 23:22, insgesamt einmal bearbeitet |
|
 |
Zepto
Anmeldungsdatum: 03.10.2007
Beiträge: 323
|
 Zepto Verfasst am: 19. Nov 2008 23:21 Titel: Zepto Verfasst am: 19. Nov 2008 23:21 Titel: |
 |
|
| Superhirn hat Folgendes geschrieben: |
Bis hier seid ihr mir doch einverstanden:
 = -v_{Gas}* (ln(m_{0}-R*t) - ln(m_{0})))
|
Nein! Du hast meine kleinen Winzbeitrag auf Seite 1 ganz am Ende nicht gelesen, oder? 
Bei der Integration hast du einen Vorzeichenfehler.
| Superhirn hat Folgendes geschrieben: |
Daraus folgt:
 = v_{Gas}* ln(\frac{m_{0}}{m_{0}-R*t}))
Die Gleichung steht auch in jedem Buch, müsste also stimmen |
Ich hab mir jetzt zwar nicht den ganzen Thread durchgelesen, aber das kann doch gar nicht sein. Wenn du für 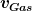 etwas negatives einsetzt, kommt für etwas negatives einsetzt, kommt für ) auch etwas negatives raus, da ja auch etwas negatives raus, da ja 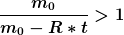 woraus dann folgt, dass die Rakete in die gleiche Richtung fliegen würde, wie ihr "Antriebsstrahl". woraus dann folgt, dass die Rakete in die gleiche Richtung fliegen würde, wie ihr "Antriebsstrahl".
Du hast also noch den Vorzeichenfehler beim Integrieren zu beheben. Dann sollte es stimmen.
Gute Nacht! 
Gruß
Zepto
Edit: Schon wieder. Das ist Absicht, ne? 
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 23:29 Titel: dermarkus Verfasst am: 19. Nov 2008 23:29 Titel: |
 |
|
| Zepto hat Folgendes geschrieben: | Das ist Absicht, ne?  |
Ich vermute, das ist Gedankenübertragung  Im Sport gibts für sowas zum Beispiel beim Synchronspringen gute Noten für Synchronität Im Sport gibts für sowas zum Beispiel beim Synchronspringen gute Noten für Synchronität 
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 19. Nov 2008 23:47 Titel: Superhirn Verfasst am: 19. Nov 2008 23:47 Titel: |
 |
|
Stimmt, jetzt hab ichs gemerkt. Dann gibt das auch einen Sinn.
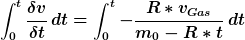
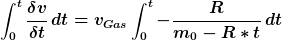
 = v_{Gas}* [ln(m_{0}-R*t)]^{t}_{0})
Ergibt:
)
Dann hat a(t) und v(t) dasselbe Vorzeichen.
Jetzt kann ich auch eine Antwort auf meine anfängliche Frage formulieren:
Da die Beschleunigung immer weiter zunimmt, nimmt auch die Geschwindigkeit immer weiter zu. Dies passiert bis zum Brennschluss t. Deswegen beschreibt auch die v(t) Funktion keine Sättigungskurve. Die Funktion wird immer steiler , für größeres t. Das sieht man aber auf dem Bild hier nicht mehr. Ist nur toll, dass uns unser Übungsleiter ne ln Funktion angezeichnet hatte und meinte die Geschwindigkeit würde immer weniger zunehmen gegen Ende...
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 23:56 Titel: dermarkus Verfasst am: 19. Nov 2008 23:56 Titel: |
 |
|
Einverstanden 
| Superhirn hat Folgendes geschrieben: | | Ist nur toll, dass uns unser Übungsleiter ne ln Funktion angezeichnet hatte und meinte die Geschwindigkeit würde immer weniger zunehmen gegen Ende... |
Sehen wirs mal positiv: Dadurch bist du dir nun sicher, dass du das ganze selbst bis auf das kleinste Vorzeichen durchüberlegt und verstanden hast 
|
|
 |
Superhirn

Anmeldungsdatum: 24.10.2006
Beiträge: 15
|
 Superhirn Verfasst am: 20. Nov 2008 00:03 Titel: Superhirn Verfasst am: 20. Nov 2008 00:03 Titel: |
 |
|
| Zitat: | | Sehen wirs mal positiv: Dadurch bist du dir nun sicher, dass du das ganze selbst bis auf das kleinste Vorzeichen durchüberlegt und verstanden hast |
Richtig, wenn man es selber durchdacht hat, dann kann man sich das Ganze auch besser merken, als wenn man es einfach so hinnimmt. Und wenn ichs einfach hingenommen hätte, dann hätte ich mir in diesem Fall auch noch was Falsches angeeignet.
Joa, dann vielen Dank euch beiden 
Gruß Superhirn
|
|
 |
|