| Autor |
Nachricht |
rakete
Gast
|
 rakete Verfasst am: 03. März 2018 00:39 Titel: Raketengleichung - konstante Ausströmgeschwindigkeit rakete Verfasst am: 03. März 2018 00:39 Titel: Raketengleichung - konstante Ausströmgeschwindigkeit |
 |
|
Hallo,
wie kann genau die Ausströmungsgeschwindigkeit relativ zur Rakete zeitlich konstant sein?
Also: v_e = v' - v, wobei v_e ist die Ausströmungsgeschwindigkeit relativ zur Rakete und v' ist die Geschwindigkeit des Treibstoffes relativ zum Boden und v ist die Geschwindigkeit der Rakete relativ zum Boden.
Wenn v' schneller als v ist, und v nimmt zu, dann wird die Differenz genau zeitlich nicht konstant oder sollte das so sein: die Geschwindigkeit von den beiden ist erhalten wegen der Energieerhaltung? Also, obwohl v zunimmt, nimmt v' ab genau mit dem gleichen Verhältnis. Ist das wie ich das verstehen sollte?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 03. März 2018 08:31 Titel: Myon Verfasst am: 03. März 2018 08:31 Titel: |
 |
|
Du musst das Ganze im System der Rakete betrachten. Die Geschwindigkeit, mit der das Gas in diesem System ausströmt, hängt v.a. ab von der Differenz des Gasdrucks im Triebwerk und dem Aussendruck. Sie wird also durch das Triebwerk bestimmt und ist zuerst einmal unabhängig vom Bewegungszustand der Rakete.
Nun ist das System der Rakete beschleunigt, und der Aussendruck ändert mit der Höhe. Die Ausströmgeschwindigkeit relativ zur Rakete wird also nicht genau konstant sein. Für grundlegende Rechnungen kann man das aber sicher annehmen.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 03. März 2018 08:39 Titel: TomS Verfasst am: 03. März 2018 08:39 Titel: |
 |
|
Ich verstehe nicht, warum du aus Sicht des ruhenden Bezugssystems, also des Bodens argumentierst.
Die technische Vorrichtung zum Ausstoß des Treibstoffs ist so konstruiert, dass letzterer eine konstante Ausströmgeschwindigkeit hat. Das sollte doch aus Sicht des mitbewegten Beobachters in der Rakete (und ohne Berücksichtigung irgendeines andren Beobachters) klar sein. Oder hast du damit bereits Problem?
Der nächste Schritt wäre dann, daraus Schlussfolgerungen für einen Beobachter auf dem Boden abzuleiten. Welche wären das? Und welche Probleme siehst du dabei?
Du sprichst von Energieerhaltung. Diese gilt immer nur für das Gesamtsystem, also Rakete plus gesamter ausgestoßener Treibstoff.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
rakete
Gast
|
 rakete Verfasst am: 03. März 2018 11:44 Titel: rakete Verfasst am: 03. März 2018 11:44 Titel: |
 |
|
Im Demtröder steht:
Die Ausströmgeschwindigkeit der Treibgase v' relativ zum Erdboden hängt von der Geschwindigkeit v der Rakete ab. Für |v| < |v'| ist v' nach unten gerichtet, für |v| > |v'| nach oben. Deshalb ist es günstiger, die Ausströmgeschwindigkeit v_e = v' -v relativ zur Rakete einzuführen, die unabhängig von v und zeitlich konstant ist...
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 03. März 2018 12:19 Titel: Myon Verfasst am: 03. März 2018 12:19 Titel: |
 |
|
Die Demtröder-Reihe gefällt mir grösstenteils sehr gut. Der Teil über die Raketengleichung aber ist m.E. nicht ganz optimal. Er wurde mit fast jeder Auflage etwas geändert, hat aber immer den ein oder anderen kleinen Fehler. In der neusten Auflage ist ungünstig, dass zu Beginn 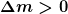 festgelegt wird, obwohl die Raketenmasse abnehmend ist. Es steht festgelegt wird, obwohl die Raketenmasse abnehmend ist. Es steht 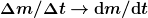 , doch in Gleichung (2.31) muss plötzlich beim Term , doch in Gleichung (2.31) muss plötzlich beim Term ) das Vorzeichen umgekehrt werden, sonst ergäbe sich nicht die korrekte Raketengleichung. das Vorzeichen umgekehrt werden, sonst ergäbe sich nicht die korrekte Raketengleichung.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 03. März 2018 14:27 Titel: TomS Verfasst am: 03. März 2018 14:27 Titel: |
 |
|
| rakete hat Folgendes geschrieben: | Im Demtröder steht:
Die Ausströmgeschwindigkeit der Treibgase v' relativ zum Erdboden hängt von der Geschwindigkeit v der Rakete ab. Für |v| < |v'| ist v' nach unten gerichtet, für |v| > |v'| nach oben. Deshalb ist es günstiger, die Ausströmgeschwindigkeit v_e = v' -v relativ zur Rakete einzuführen, die unabhängig von v und zeitlich konstant ist... |
Und weil der zweite Satz offensichtlich richtig ist, braucht es den ersten überhaupt nicht. Er ist m.E. irrelevant.
Was genau ist jetzt dein Problem?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
rakete
Gast
|
 rakete Verfasst am: 04. März 2018 11:21 Titel: rakete Verfasst am: 04. März 2018 11:21 Titel: |
 |
|
Na ja du hast erst gefragt wieso ich die Geschwindigkeit vom Boden betrachtet habe...solltest du denn Demtröder fragen, wieso er das gemacht hat.
Danke Myon für die Erkenntnis. Weißt du ein anderes Buch bzw. eine Website, die ich eine gute Erklärung für die Raketegleichung lesen kann? Vor allem, hast du ein anderes Lehrbuch, das du mir empfehlen kannst, um Ex I-IV zu lernen? Demtröder ist gut aber ich finde am manchen Stellen sind die Herleitungen und Erklärungen überhaupt nicht optimal.
Meine Frage noch ist: wieso ist v_e konstant, wenn die Geschwindigkeit der Rakete natürlich nimmt sehr schnell zu and die Geschwindigkeit des Treibstoffes bleibt "konstant"?
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 04. März 2018 11:50 Titel: jh8979 Verfasst am: 04. März 2018 11:50 Titel: |
 |
|
| rakete hat Folgendes geschrieben: | | Demtröder ist gut .... |
Nein. Demtröder ist ein furchtbares Buch, insbesondere was mathematische Herleitungen angeht...
| Zitat: | aber ich finde am manchen Stellen sind die Herleitungen und Erklärungen überhaupt nicht optimal.
|
Sag ich ja 
| Zitat: |
Meine Frage noch ist: wieso ist v_e konstant, wenn die Geschwindigkeit der Rakete natürlich nimmt sehr schnell zu and die Geschwindigkeit des Treibstoffes bleibt "konstant"? |
v_e ist die Austrittsgeschwindigkeit im Ruhesystem der Rakete... da ist es egal wie schnell die Rakete schon ist.
|
|
 |
rakete
Gast
|
 rakete Verfasst am: 04. März 2018 12:11 Titel: rakete Verfasst am: 04. März 2018 12:11 Titel: |
 |
|
Welche Bücher gefallen dir denn? 
Ja ok so wir sind in der Rakete. Das System ist in Ruhe. Aber der Moment, indem das System beschleunigt würde, wird sich die Austrittsgeschwindigkeit ändern.
Ich verstehe auch nicht wir die Austrittsgeschwindigkeit "unabhängig" von der Geschwindigkeit der Rakete ist, wenn in der Formel die Geschwindigkeit der Rakete da ist.
Vielleicht brauche ich einfach bessere Bücher 
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 04. März 2018 12:28 Titel: Mathefix Verfasst am: 04. März 2018 12:28 Titel: |
 |
|
| rakete hat Folgendes geschrieben: | Welche Bücher gefallen dir denn? 
Ja ok so wir sind in der Rakete. Das System ist in Ruhe. Aber der Moment, indem das System beschleunigt würde, wird sich die Austrittsgeschwindigkeit ändern.
Ich verstehe auch nicht wir die Austrittsgeschwindigkeit "unabhängig" von der Geschwindigkeit der Rakete ist, wenn in der Formel die Geschwindigkeit der Rakete da ist.
Vielleicht brauche ich einfach bessere Bücher  |
Die Annahme ist, dass der Treibsatz der Rakete mit einem konstanten Massenstrom abbrennt.
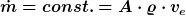
A = Düsenfläche
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 04. März 2018 13:14 Titel: jh8979 Verfasst am: 04. März 2018 13:14 Titel: |
 |
|
| rakete hat Folgendes geschrieben: | Welche Bücher gefallen dir denn? 
|
Den Giancoli find ich ganz gut, Tipler ist auch ok... wenn ich mich jetzt auf ein Buch festlegen müßte
| Zitat: |
Ja ok so wir sind in der Rakete. Das System ist in Ruhe. Aber der Moment, indem das System beschleunigt würde, wird sich die Austrittsgeschwindigkeit ändern.
Ich verstehe auch nicht wir die Austrittsgeschwindigkeit "unabhängig" von der Geschwindigkeit der Rakete ist, wenn in der Formel die Geschwindigkeit der Rakete da ist.
|
Im wesentlichen ist das die Aussage des Relativitätsprinzips: Der Motor funktioniert genau gleich, egal ob er sich bewegt oder nicht. Der Brennstoff wird also relativ zum Motor immer mit derselben Geschwindigkeit ausgestoßen.
|
|
 |
Portisch
Gast
|
 Portisch Verfasst am: 04. März 2018 13:35 Titel: Portisch Verfasst am: 04. März 2018 13:35 Titel: |
 |
|
| Zitat: | | Aber der Moment, indem das System beschleunigt würde, wird sich die Austrittsgeschwindigkeit ändern. |
Das stimmt, den indem Moment wo das passiert würde die Rakete ein beschleunigtes Bezugssystem sein und die Trägheitskraft den verbrannten Treibstoff zusätzlich beschleunigen natürlich ändert sich auch deren Größe je nach momentanter Beschleunigung
In der Herleitung der Raketengleichung geht man einfach davon aus die Gase immer mit gleicher Geschwindigkeit auf die Rakete bezogen diese verlassen.
Stell dir halt vor da ist eine Art Regelkreisfall der die austrittsgeschwindigkeit immer gleich regelt.
Das ist einfach leichter zu rechnen-
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. März 2018 17:52 Titel: TomS Verfasst am: 04. März 2018 17:52 Titel: |
 |
|
| Portisch hat Folgendes geschrieben: | | Zitat: | | Aber der Moment, indem das System beschleunigt würde, wird sich die Austrittsgeschwindigkeit ändern. |
Das stimmt, den indem Moment wo das passiert würde die Rakete ein beschleunigtes Bezugssystem sein und die Trägheitskraft den verbrannten Treibstoff zusätzlich beschleunigen natürlich ändert sich auch deren Größe je nach momentanter Beschleunigung |
Das ist ziemlich sinnfrei.
| rakete hat Folgendes geschrieben: | | wieso ist v_e konstant, wenn die Geschwindigkeit der Rakete natürlich nimmt sehr schnell zu and die Geschwindigkeit des Treibstoffes bleibt "konstant"? |
Die Geschwindigkeit des zu einem bestimmten Zeitpunkt ausgestoßenes Treibstoffs ist aus Sicht der Rakete zu jedem Zeitpunkt gleich. Die Geschwindigkeit des früher ausgestoßenen Treibstoffs ist bei der Betrachtung völlig irrelevant.
Man betrachtet ein infinitesimales Zeitintervall dt. Innerhalb dessen wird eine infinitesimale Masse Treibstofff dm ausgestoßen; stell dir vor, statt des Treibstoffs wirft der Pilot einen winzigen Stein der Masse dm mit einer Geschwindigkeit v_e nach hinten. Warum soll dieses v_e aus Sicht des werfenden Piloten nicht konstant sein?
Durch den Ausstoß reduziert sich die Masse der Rakete um dm, und es erhöht sich die Geschwindigkeit umdv.
Der Gesamtimpuls p des Gesamtsystems bestehend aus Rakete und Treibstoff ist zu jedem Zeitpunkt erhalten. Wir betrachten dies nun im Ruhesystem eines ortsfesten Beobachters auf dem Boden.
 - dm\,(v - v_e))
Der erste Term entspricht der Impulsänderung der Rakete, der zweite Term entspricht dem Impuls des gerade ausgestoßenen Treibstoffs - jeweils betrachtet im Ruhesystem eines ortsfesten Beobachters, aus dessen Sicht die Rakete die Geschwindigkeit v hat.
Anwenden der Produktregel auf den ersten Term und Zusammenfassen liefert
 - dm\,(v - v_e) = dm\,v + m\,dv - dm\,v + dm\,v_e = m\,dv + dm\,v_e)
Daraus folgt die gesuchte Differentialgleichung.
|
|
 |
Portisch
Gast
|
 Portisch Verfasst am: 04. März 2018 19:33 Titel: Portisch Verfasst am: 04. März 2018 19:33 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Das ist ziemlich sinnfrei. |
Was genau ist das sinnfrei? Ich habe ihn so verstanden, das ein festmontiertes Raktetentriebwerk, das Gas mit einer gewissen Austrittsgeschwindigkeit vg auswirft. Wenn nun das ganze System aber beschleunigt verändert sich dieses vg weil das ganze System noch selbst beschleunigt. dadurch verändert sich die Geschwindigkeit zusätzlich bis das Gas die Systemgrenze erreicht. Das erklärt sich im Inertialsystem dadurch das die Rakete selbst beschleunigt und im beschleunigten Bezugssystem des Pilot durch die nun auftretende Trägheitskraft.
| TomS hat Folgendes geschrieben: | | Warum soll dieses v_e aus Sicht des werfenden Piloten nicht konstant sein? |
Weil der Pilot selbst beschleunigt, wenn er immer wieder Steine wirft und diese Steine eine gewisse Zeit brauchen bis sie die Systemgrenze erreicht haben
|
|
 |
Portisch
Gast
|
 Portisch Verfasst am: 04. März 2018 20:31 Titel: Portisch Verfasst am: 04. März 2018 20:31 Titel: |
 |
|
Nachtrag.
Man stelle sich ein mit handbremse angezogenes Auto vor in der eine Person nach hinten immer wieder Steine wirft, die durch das Auto fliegen und am Ende des Autos mit vg austreten.
Würde nun aber die Handbremse gelöst, würde das Auto beschleunigen und sich das ve bis zum Austritt des Steins hinten am Auto verändern, weil das Auto selbst beschleunigt.
Im bezugssystem des Auto selbst erklärt sich das nun, das hier jetzt zusätzlich eine Trägheitskraft auf den Stein wirkt.
Das gleiche gilt für die Gasteilchen die im Raketentriebwerk beschleunigt werden und am Ende des Raktentriebwerks (systemgrenze) mit vg austreten.
Ich hoffe ich habe das jetzt annähernd verständlich hingeschrieben.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. März 2018 22:21 Titel: TomS Verfasst am: 04. März 2018 22:21 Titel: |
 |
|
| Portisch hat Folgendes geschrieben: | | Wenn nun das ganze System aber beschleunigt verändert sich dieses v_e weil das ganze System noch selbst beschleunigt. |
Nein, v_e ändert sich nicht bzgl. der jeweiligen Inertialsysteme!
Die Rakete habe zu Zeitpunkten t₁, t₂, … die Geschwindigkeiten v₁, v₂, … bzgl. des ruhenden Bezugssystems I₀ = der Startrampe.
Dadurch werden Inertialsysteme I₁, I₂, … definiert, die sich gegenüber dem ruhenden Bezugssystem mit genau diesen Geschwindigkeiten v₁, v₂, ... bewegen. Die Rakete selbst definiert kein Inertialsystem, da sie beschleunigt ist; aber zu jedem einzelnen Zeitpunkt kann ihr ein Inertialsystem zugeordnet werden, bzgl. dessen sie genau zu diesem Zeitpunkt ruht.
Und bzgl. jedes dieser Inertialsysteme I₁, I₂, … hat der ausströmende Treibstoff zu jedem Zeitpunkt t₁, t₂, … immer die selbe Geschwindigkeit vg. Natürlich hat der zu t = t₂ ausgestoßene Treibstoff bzgl. I₁ eine andere Geschwindigkeit, aber diese ist irrelevant und wird nie betrachtet. Dass die Rakete beschleunigt ist für die Treibstoffgeschwindigkeiten bzgl. der Inertialsysteme I₁, I₂, … irrelevant.
| Portisch hat Folgendes geschrieben: | | dadurch verändert sich die Geschwindigkeit zusätzlich bis das Gas die Systemgrenze erreicht. |
Welche Systemgrenze?
| Portisch hat Folgendes geschrieben: | | Das erklärt sich im Inertialsystem dadurch, dass die Rakete selbst beschleunigt und im beschleunigten Bezugssystem des Pilot durch die nun auftretende Trägheitskraft. |
Die Beschleunigung und das beschleunigte Bezugssystem sind irrelevant. Man kann dies alles mittel der o.g. Inertialsysteme formulieren.
| Portisch hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Warum soll dieses v_e aus Sicht des werfenden Piloten nicht konstant sein? |
Weil der Pilot selbst beschleunigt, wenn er immer wieder Steine wirft und diese Steine eine gewisse Zeit brauchen bis sie die Systemgrenze erreicht haben |
Meines Erachtens denkst du viel zu kompliziert.
| Portisch hat Folgendes geschrieben: | | Würde nun aber die Handbremse gelöst, würde das Auto beschleunigen und sich das v_e bis zum Austritt des Steins hinten am Auto verändern, weil das Auto selbst beschleunigt. |
Bzgl. welches Bezugsystems? Kannst du das mal präzise definieren?
| Portisch hat Folgendes geschrieben: | | Im Bezugssystem des Auto selbst erklärt sich das nun, das hier jetzt zusätzlich eine Trägheitskraft auf den Stein wirkt. |
Wie gesagt, m.E. denkst du viel zu kompliziert. Wenn von „im Bezugssystem des Autos bzw. der Rakete“ die Rede ist, dann ist immer das zum jeweiligen Zeitpunkt gedachte Inertialsystem gemeint.
Wenn du eine Quelle hast, die auf derlei komplizierte Weise mit Systemgrenzen und Trägheitskräften argumentiert, dann solltest du sie am besten vergessen.
| Portisch hat Folgendes geschrieben: | | Ich hoffe ich habe das jetzt annähernd verständlich hingeschrieben. |
Ja. Ich fürchte einfach, du hast eine wenig sinnvolle Erklärung gelesen; m.E. kann man das erheblich einfacher darstellen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2018 22:44 Titel: DrStupid Verfasst am: 04. März 2018 22:44 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Bzgl. welches Bezugsystems? Kannst du das mal präzise definieren? |
Es ist präztise definiert. v_e bezieht sich auf das Ruhesystem der Rakete. Wenn Du die Argumentation von Portisch verstehen willst, dann musst Du aufhören zwanghaft in tangential mitbewegten Bezugssystemen zu denken. Das Ruhesystem der Rakete ist kein Inertialsystem und das hat einen Einfluss auf die Austrittsgeschwindigkeit des Gases in diesem Bezugssystem.
Möglicherweise irritiert Dich die Tatsache, dass der Effekt normalerweise vernachlässigbar klein ist. In dem Fall könnte es helfen, wenn Du Dir überlegst, was in dem Extremfall passiert, dass die Austrittsgeschwindigkeit im ruhenden Triebwerk Null ist - z.B. weil die Pumpe für eine Treibstoffkomponente defekt ist. Um sinnlosen Nebendiskussionen vorzubeugen, kannst Du zusätzlich annehmen, dass die Rakete horizontal auf der Erde liegt, die von der noch funktionierenden Pumpe geförderte Treibstoffkomponente flüssig ist und die Rakete noch weitere, funktionierende Triebwerke hat. Dann sammelt sich der Treibstoff in der ruhenden Rakete einfach in der Brennkamer, bis er mit v_e=0 (in horizontaler Richtung) herausläuft. Was passiert wohl, wenn die anderen Triebwerke zünden und die Rakete horizontal beschleunigt? Ist das v_e im kaputten Triebwerk dann immer noch Null?
|
|
 |
Portisch
Gast
|
 Portisch Verfasst am: 04. März 2018 22:45 Titel: Portisch Verfasst am: 04. März 2018 22:45 Titel: |
 |
|
Hi, TomS
| Zitat: | | welche Systemgrenze? |
Wenn wir von der Rakete sprechen, das Triebwerksende bei dem das Gas fertig beschleunigt auf das Intertialsystem austritt, weil sonst wirds komplizierter.
Das Triebwerk hat eine gewisse Länge in der die Gasteilchen am Anfang beim Eintritt ins Triebwerk aus der Sicht der Rakete ruhen und dann in Etappen durch die Triebwerkslänge durchbeschleunigt werden und am Ende fertigbeschleunigt mit vg austreten.
Dieser Vorgang dauert für jedes Gasteilchen eine gewisse Zeit.
Wenn das Triebwerk auf der Erde irgendwo am Boden fix montiert ist wirkt auf die Gasteilchen in Beschleunigungsrichtung ausschließlich chemische Wechselwirkungen.
wenn die Rakete aber beschleunigt wirken aus der Sicht der Rakete im Triebwerk zusätzlich neben der chemischen Wechselwirkung noch die Trägheitskräfte auf die Gasteilichen die dadurch über die Strecke zusätzlich beschleunigt werden und am ende mit einen größeren vg aus der Sicht der Rakete herauskommen.
Aus dem Inertialsystem gesehen kann man die größere Austrittsgeschwindigkeit die der Pilot aus der Rakete nun wahrnimmt ebenfalls erklären, dadurch das die Rakete selbst in die andere Richtung beschleunigt.
und ich denke genau das hat der Threadsteller gemeint. das einfach die Austrittsgeschwindigkeit aus der Sicht der Rakete schneller sein müsste als bei einem fix am Boden montierten Raketentriebwerk.
In der Raktengleichung bezieht man die Austrittsgeschwindigkeit vg auf die Rakete und betrachtet diese als konstant. Das das Triebwerk eine gewisse Länge hat übergeht man. Das ist auch berechtigt, weil der Fehler klein ist.
Ich denke es geht dem Threadsteller genau darum, aber ich kann mich auch täuschen
| Zitat: | Meines Erachtens denkst du viel zu kompliziert.
|
kann sein, was ist denn deine Aussage. Ein fix am Boden montiertes Triebwerk schleudert die Gase aus der Sicht eines am boden befindlichen Beobachters mit einer Geschwindkeit aus. ein beschleunigtes Raketentriebwerk, schleudert die Gase aus der Sicht des Piloten genau gleich schnell aus?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 05. März 2018 06:44 Titel: TomS Verfasst am: 05. März 2018 06:44 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Wenn Du die Argumentation von Portisch verstehen willst, dann musst Du aufhören zwanghaft in tangential mitbewegten Bezugssystemen zu denken. |
Kommt dabei am Ende was anderes raus?
| DrStupid hat Folgendes geschrieben: | | Das Ruhesystem der Rakete ist kein Inertialsystem und das hat einen Einfluss auf die Austrittsgeschwindigkeit des Gases in diesem Bezugssystem. |
Kannst du mir das vorrechnen?
| DrStupid hat Folgendes geschrieben: | | Möglicherweise irritiert Dich die Tatsache, dass der Effekt normalerweise vernachlässigbar klein ist. |
OK, dann berechne mir doch bitte die Korrektur zur Raketengleichung, die sich aus deiner Überlegung ergibt. Ich bin gespannt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 05. März 2018 07:03 Titel: TomS Verfasst am: 05. März 2018 07:03 Titel: |
 |
|
| Portisch hat Folgendes geschrieben: | Das Triebwerk hat eine gewisse Länge in der die Gasteilchen am Anfang beim Eintritt ins Triebwerk aus der Sicht der Rakete ruhen und dann in Etappen durch die Triebwerkslänge durchbeschleunigt werden und am Ende fertigbeschleunigt mit vg austreten.
Dieser Vorgang dauert für jedes Gasteilchen eine gewisse Zeit.
Wenn das Triebwerk auf der Erde irgendwo am Boden fix montiert ist wirkt auf die Gasteilchen in Beschleunigungsrichtung ausschließlich chemische Wechselwirkungen.
wenn die Rakete aber beschleunigt wirken aus der Sicht der Rakete im Triebwerk zusätzlich neben der chemischen Wechselwirkung noch die Trägheitskräfte auf die Gasteilichen die dadurch über die Strecke zusätzlich beschleunigt werden und am ende mit einen größeren vg aus der Sicht der Rakete herauskommen.
Aus dem Inertialsystem gesehen kann man die größere Austrittsgeschwindigkeit die der Pilot aus der Rakete nun wahrnimmt ebenfalls erklären, dadurch das die Rakete selbst in die andere Richtung beschleunigt |
Du möchtest also den Prozess in der Brennkammer selbst beschreiben und die Idealisierung, dass eine infinitesimale Brennstoffmenge instantan auf die Austrittsgeschwindigkeit beschleunigt wird, aufgeben.
Welcher Effekt könnte sich dadurch ergeben?
Ich denke, du stimmst mir zu, dass die von mir o.g. Austrittsgeschwindigkeiten zu Zeitpunkten t₁, t₂, … und jeweils bzgl. der Inertialsysteme I₁, I₂, … nicht variieren können; dies würde eine Verletzung der Galilei-Invarianz bedeuten.
Im Folgenden bezeichne u die Austrittsgeschwindigkeit für einen beliebigen Zeitpunkt t₁, t₂, …, jeweils gemessen bzgl. des zu diesem Zeitpunkt gültigen Inertialsystem I₁, I₂, …, das ggü. dem ruhenden Bezugsystem gerade die Geschwindigkeit v₁, v₂, … der Rakete habe.
Dann gilt
|_{I_1} = u_2(t_2)|_{I_2} = \ldots = v_e)
Oder bestreitest du das?
EDIT - zur Systemgrenze: Die Austrittsgeschwindigkeit muss natürlich an einem Punkt definiert und gemessen werden, ab dem das Gas gerade dynamisch vollständig von der Rakete entkoppelt ist und keinerlei Impulsübertrag (Rückstoß) mehr auf die Rakete übertragen wird. Damit kann ab hier eine rein kinematische Betrachtung vorgenommen werden. Dies ist auch die sinnvolle Definition der Systemgrenze. Die so definierte Austrittsgeschwindigkeit wird aus Sicht beliebiger Inertialsysteme immer identisch gemessen werden (wenn man eine Vorrichtung hat, die an diesem Punkt messen kann).
Oder bestreitest du das?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 05. März 2018 09:02 Titel: TomS Verfasst am: 05. März 2018 09:02 Titel: |
 |
|
| Portisch hat Folgendes geschrieben: | | Zitat: | | welche Systemgrenze? |
Wenn wir von der Rakete sprechen, das Triebwerksende bei dem das Gas fertig beschleunigt auf das Intertialsystem austritt |
Ja.
| Portisch hat Folgendes geschrieben: | | Das Triebwerk hat eine gewisse Länge in der die Gasteilchen am Anfang beim Eintritt ins Triebwerk aus der Sicht der Rakete ruhen und dann in Etappen durch die Triebwerkslänge durchbeschleunigt werden und am Ende fertigbeschleunigt mit vg austreten. |
Ja.
| Portisch hat Folgendes geschrieben: | | Dieser Vorgang dauert für jedes Gasteilchen eine gewisse Zeit. |
Ja.
| Portisch hat Folgendes geschrieben: | | Wenn die Rakete aber beschleunigt wirken aus der Sicht der Rakete im Triebwerk zusätzlich neben der chemischen Wechselwirkung noch die Trägheitskräfte auf die Gasteilichen die dadurch über die Strecke zusätzlich beschleunigt werden und am ende mit einen größeren vg aus der Sicht der Rakete herauskommen. |
Interessanter Gedanke.
| Portisch hat Folgendes geschrieben: | | Aus dem Inertialsystem gesehen kann man die größere Austrittsgeschwindigkeit die der Pilot aus der Rakete nun wahrnimmt ebenfalls erklären, dadurch das die Rakete selbst in die andere Richtung beschleunigt. |
Moment: der Pilot und das Ende der Triebswerks definieren zu einem bestimmten Zeitpunkt ein und das selbe (gedachte) Inertialsystem. Deshalb muss die so definierte Austrittsgeschwindigkeit trivialerweise identisch sein. Wann und warum soll der Pilot eine größere Austrittsgeschwindigkeit wahrnehmen können? Es gibt nicht einmal zwei verschiedene Definitionen oder Messungen, sondern imme nur genau eine, nämlich die bzgl. des mit der Rakete mitbewegten Inertialsystems = des zum Zeitpunkt des Austritts momentanen Ruhesystems. Wenn zwei verschiedene Geschwindigkeiten vorliegen sollen, dann müsstest du zunächst mal zwei verschiedene Definitionen und Messungen spezifizieren.
| Portisch hat Folgendes geschrieben: | | In der Raktengleichung bezieht man die Austrittsgeschwindigkeit vg auf die Rakete und betrachtet diese als konstant. Das das Triebwerk eine gewisse Länge hat übergeht man. Das ist auch berechtigt, weil der Fehler klein ist. |
Warum sollte überhaupt ein Fehler vorliegen, wenn ich eine einzige konsistente Definition vornehme und durchgehend verwende?
Ein Fehler tritt dann auf, wenn ich z.B. implizit zwei Definitionen einführe und vermische.
| Portisch hat Folgendes geschrieben: | | Ich denke es geht dem Threadsteller genau darum, aber ich kann mich auch täuschen. |
Ok, verstanden.
Aber dann sollte man wohl nicht von einem kleinen Fehler in der Herleitung sprechen, sondern von einer Verwechslung oder Vermischung von Definitionen o.ä.
Wenn tatsächlich ein noch so kleiner Fehler in dieser rein kinematischen Betrachtung vorliegen sollte, dann würde mich eine mathematische Herleitung interessieren, sowie ein konkrete Kritik an dem o.g. Argument bzgl. Galileiinvarianz.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 05. März 2018 11:54 Titel: VeryApe Verfasst am: 05. März 2018 11:54 Titel: |
 |
|
Ich logge mich mal ein damit ich meine Beiträge editieren kann, die offensichtlich jetzt länger werden müssen.
| Zitat: | Du möchtest also den Prozess in der Brennkammer selbst beschreiben und die Idealisierung, dass eine infinitesimale Brennstoffmenge instantan auf die Austrittsgeschwindigkeit beschleunigt wird, aufgeben.
Welcher Effekt könnte sich dadurch ergeben? |
Ich will das eigentlich nicht. Ich wollte nur den Threadsteller helfen, der sich offensichtlich tiefere Gedanken macht, er soll sich einfach einen Regelkreis vorsellen der vg konstant hält. Die Rechnung wird ziemlich einfach und der Fehler ist gering.
Da ergeben sich mehrere Effekte wie der zum Beispiel, das der ermittelte Impuls des Raketensystems den Impuls des Raketengrundkörpers plus des Impulses der Gasteilchen die sich in den Triebwerk befinden beschreibt. da die eine andere Geschwindigkeit haben also der Raketengrundkörper. Sie bewegen sich zurück, beschreibt die Geschwindigkeit v =pges/mges nicht die Geschwindigkeit des Grundkörpers sondern des ganzen Systems.
Stimmt also nur näherungsweise für die eigentliche Rakete, die müsste sich eine Spur schneller bewegen.
Desweiteren ergeben sich auch Effekte der Veränderung der Austrittsgeschwindigkeit. Das alles ist aber nicht schlimm, weil die Näherung sehr genau ist, unter anderem kompensieren sich sogar einige fehler durch die Idealisierung
| Zitat: | Im Folgenden bezeichne u die Austrittsgeschwindigkeit für einen beliebigen Zeitpunkt t₁, t₂, …, jeweils gemessen bzgl. des zu diesem Zeitpunkt gültigen Inertialsystem I₁, I₂, …, das ggü. dem ruhenden Bezugsystem gerade die Geschwindigkeit v₁, v₂, … der Rakete habe.
Dann gilt
|_{I_1} = u_2(t_2)|_{I_2} = \ldots = v_e)
Oder bestreitest du das?
|
Ich bestreite davon gar nichts, du verstehst nicht was ich meine.
| Zitat: |
Moment: der Pilot und das Ende der Triebswerks definieren zu einem bestimmten Zeitpunkt ein und das selbe (gedachte) Inertialsystem. Deshalb muss die so definierte Austrittsgeschwindigkeit trivialerweise identisch sein.
|
das bestreite ich auch nicht. Beide ermitteln die vergrößerte Austrittsgeschwindigkeit.
Betrachte t1 sei der Zeitpunkt an dem das Gasteilchen beginnt zu beschleunigen und t2 der Zeitpunkt an dem das Gasteilchen fertig beschleunigt austritt. Du mußt schon die Zeitspanne 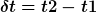 die es sich im Triebwerk befindet betrachten. die es sich im Triebwerk befindet betrachten.
In der Rakete wirkt über die Zeitspanne zusätzlich die Trägheitskraft auf das Gasteilchen, die sich je nach momentaner Beschleunigung a(t) ergibt.
aus der Sicht des Inertialsystems beschleunigt die Rakete über diese Zeitspanne entgegen des Gasteilchens, beides führt zu ein und denselben Resultat. das die Austrittsgeschwindigkeit aus dem Triebwerk sowohl vom Inertialsystem betrachtet bezogen auf die Rakete wie auch vom Piloten zum Zeitpunkt t2 größer ist,
als wäre das Raktentriebwerk fix am Boden montiert.
| Zitat: | Warum sollte überhaupt ein Fehler vorliegen, wenn ich eine einzige konsistente Definition vornehme und durchgehend verwende?
Ein Fehler tritt dann auf, wenn ich z.B. implizit zwei Definitionen einführe und vermische.
|
Du schreibst doch oben selbst von einer Idealisierung. Idealisierung haben doch an sich das sie nur eine Näherung sind und somit zwangsweise einen Fehler enthalten, Wie sollte man das jetzt nennen.
Von mir aus schreibe ich Näherung.
| Zitat: | Ok, verstanden.
Aber dann sollte man wohl nicht von einem kleinen Fehler in der Herleitung sprechen, sondern von einer Verwechslung oder Vermischung von Definitionen o.ä.
Wenn tatsächlich ein noch so kleiner Fehler in dieser rein kinematischen Betrachtung vorliegen sollte, dann würde mich eine mathematische Herleitung interessieren, sowie ein konkrete Kritik an dem o.g. Argument bzgl. Galileiinvarianz.
|
Ich wollte hier eigentlich keine größere Raketendiskussion auslösen. Ich wollte den Threadsteller nur helfen. Dasselbe Problem hatte ich auch gehabt. Einfach denken das fließt konstant aus der Fehler ist gering die Rechnung ist einfach und fertig.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 05. März 2018 14:38 Titel: TomS Verfasst am: 05. März 2018 14:38 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | Ich logge mich mal ein damit ich meine Beiträge editieren kann, die offensichtlich jetzt länger werden müssen. |
Und damit man weiß, wer du bist :-)
Gibt es jetzt einen zumindest berechenbaren Effekt? Welchen?
| VeryApe hat Folgendes geschrieben: | Da ergeben sich mehrere Effekte wie der zum Beispiel, das der ermittelte Impuls des Raketensystems den Impuls des Raketengrundkörpers plus des Impulses der Gasteilchen die sich in den Triebwerk befinden beschreibt. da die eine andere Geschwindigkeit haben also der Raketengrundkörper. Sie bewegen sich zurück, beschreibt die Geschwindigkeit v =pges/mges nicht die Geschwindigkeit des Grundkörpers sondern des ganzen Systems.
Stimmt also nur näherungsweise für die eigentliche Rakete, die müsste sich eine Spur schneller bewegen. |
Kannst du das berechnen?
| VeryApe hat Folgendes geschrieben: | | Desweiteren ergeben sich auch Effekte der Veränderung der Austrittsgeschwindigkeit. |
Welche? Kannst du das berechnen?
| VeryApe hat Folgendes geschrieben: | | Beide ermitteln die vergrößerte Austrittsgeschwindigkeit. |
Vergrößert im Vergleich zu was?
| VeryApe hat Folgendes geschrieben: | | ... als wäre das Raktentriebwerk fix am Boden montiert. |
Betrachten wir diesen Fall der fest am Boden verankerten Rakete. Das entspricht offensichtlich einer extrem vergrößerten Masse, d.h. statt der Raketenmasse m müssen wir die Masse der Rakete m plus die Masse der Erde M ansetzen (und wir denken uns, dass die Rakete den Treibstoff nach oben ausstößt, so dass dieser nicht direkt auf die Erdoberfläche prallt).
Die ursprüngliche Gleichung lautet

Für die fest montierte Rakete gilt dann
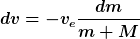
OK? Oder nicht OK?
Das ist vielleicht interessant:
http://www.clavius.info/Susanne/RFS-Skript_(Uni-Muenchen).pdf
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 05. März 2018 19:40 Titel: DrStupid Verfasst am: 05. März 2018 19:40 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Kommt dabei am Ende was anderes raus? |
Das hängt von den Umständen ab. Es wäre aber schon ein sehr großer Zufall, wenn die Scheinkräfte des beschleunigten Systems und die daraus resultierenden Änderungen der Wechselwirkungskräfte sich gegenseitig exakt aufheben. Das glaube ich Dir erst wenn Du es vorrechnest.
| DrStupid hat Folgendes geschrieben: | | Kannst du mir das vorrechnen? |
Das kann beliebig kompliziert werden. Die zusätzliche Beschleunigung durch die Trägheitskräfte hängt davon ab, wie das Gas durch die Wechselwirkungskräfte im und außerhalb des Raketenmotors beschleunigt wird. Und als ob das allein nicht schon kompliziert genug wäre, hängen die Wechselwirkungskräfte wiederum von der zusätzlichen Beschleunigung ab.
Wie man die zusätzliche Geschwindigkeit für den stark vereinfachten Fall berechnen kann, dass die Wechselwirkungskräfte unabhängig von der Beschleunigung sind, hat VeryApe oben schon beschrieben. Leider ist dieser einfache Ansatz in der Praxis wenig hilfreich, weil man dafür die Zeit benötigt, in der der Treibstoff bis zur Ausströmgeschwindigkeit beschleunigt wird. Mit den für reale Raketenmotoren dokumentierten Parametern sind weitere vereinfachende Annahmen notwendig, um wenigstens zu einer groben Abschätzung zu kommen. Dazu gehört beispielsweise eine gleichförmige Beschleunigung und das Erreichen der Ausströmgeschwindigkeit an der Mündung der Düse. Das ergibt

Wobei a die als konstant angenommene Beschleunigung des Gases von der Einspritzung in die Brennkammer bis zur Mündung der Düse und s der dabei zurückgelegt Weg ist. Im Ruhesystem des Motors hängt s nur von seinen Dimensionen ab. Die Beschleunigung setzt sich zusammen aus der Beschleunigung 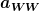 aufgrund der Wechselwirkungskräfte und der Beschleunigung aufgrund der Wechselwirkungskräfte und der Beschleunigung 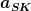 durch die Scheinkräfte im beschleunigten System: durch die Scheinkräfte im beschleunigten System:

Da die Wechselwirkungskräfte als unabhängig von der Beschleunigung angenommen wurden, kann 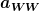 durch Umstellen obiger Gleichung aus der Austrittsgeschwindigkeit durch Umstellen obiger Gleichung aus der Austrittsgeschwindigkeit 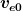 des ruhenden Motors berechnet werden: des ruhenden Motors berechnet werden:

Im konkreten Fall eines Vulcain 1 Triebwerks mit einer Länge von 3 Metern und einer Austrittsgeschwindigkeit von 4228 km/s ergibt das rund 3·10^6 m/s². An dieser Stelle wird bereits deutlich, warum der Einsfluss der zusätzlichen 4 g eines typischen Ariane-Starts getrost vernachlässigt werden können. Wenn man trotzdem weiterrechnet, dann kommt am Ende eine Erhöhung der Austrittsgeschwindigkeit um lächerliche 2,8 mm/s heraus. Das liegt weit unterhalb der Schwankungen im normalen Betrieb.
| DrStupid hat Folgendes geschrieben: | | OK, dann berechne mir doch bitte die Korrektur zur Raketengleichung, die sich aus deiner Überlegung ergibt. |
Wie meine obige Abschätzung zeigt, gibt es da nicht viel zu korrigieren. Und selbst wenn man hier unbedingt eine Korrektur durchführen will, dann ist das ganz einfach durch Verwendung des spezifischen Impulses anstelle der Ausströmgeschwindigkeit 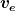 möglich. Der spezifischen Impuls ist im Rahmen der obigen Vereinfachungen und unter nicht-relativistischen Bedingungen gleich der Ausströmgeschwindigkeit möglich. Der spezifischen Impuls ist im Rahmen der obigen Vereinfachungen und unter nicht-relativistischen Bedingungen gleich der Ausströmgeschwindigkeit 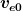 des ruhenden Motors. des ruhenden Motors.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 05. März 2018 20:30 Titel: VeryApe Verfasst am: 05. März 2018 20:30 Titel: |
 |
|
| Zitat: | Gibt es jetzt einen zumindest berechenbaren Effekt? Welchen?
|
Leider kann ich das bezüglich des ersten Effekts das die Rakete eine spur schneller fliegen müsste nur abschätzen
und im zweiten Fall betreffend der Ausströmgeschwindigkeit nur durch logisches Denken und durch die kurze Zeit die sich das Gasteilchen im Triebwerk befindet abschätzen das sich da nicht viel an der Geschwindigkeit verändern kann, weil die Zeit einfach nicht ausreicht.
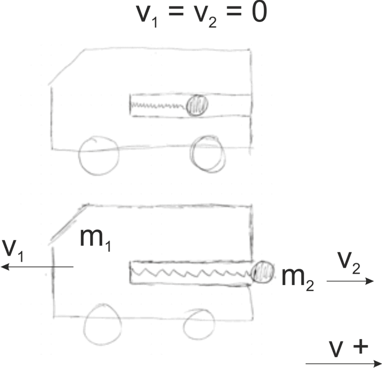
Ich kann dir aber anhand eines einfachen Beispiels: Im Spielzeugauto ist eine masselose Feder gespannt die einen Stein wegschießt. Die Feder ist so positioniert das bei völliger entspannung der Stein das auto verlässt
Das Auto ist zunächst blockiert. das heißt die Masse der Erde ist im Spiel und das Auto wird samt Erde fast nicht beschleunigt.
Die Lagerenergie der Feder strömt nur auf den Stein-
Danach wird das Auto nicht mehr blockiert. Energie fließt auf stein und Auto.
Wie ist die Austrittsgeschwindigkeit in beiden Fällen zum Auto.
Da kann man einfach impulserhaltung und energieerhaltung anwenden.
Noch einfacher ist es wenn ich die Feder mit einer konstanten Kraft über den Weg wirken lasse, dann könnte ich die sogar den zeitlichen Verlauf aus beiden Systemen mathematisch beschreiben
Aber eigentlich will ich diese Woche noch am Abend World of Tanks spielen.Ich habe nicht gewußt, daß ich jetzt noch Ableitungen hinschreiben muß, ich dachte eigentlich das wäre den meisten klar. 
| Zitat: | | Kannst du das berechnen? |
also zu dem Effekt das die Rakete sich ein wenig schneller bewegen müsste.
Ich habe dazu das ganze System Rakete samt Triebwerk in zwei Untersysteme zerlegt in einen Grundkörper und in einen Triebwerksinhaltskörper.
Alles was zum Grundkörper zählt hat definitiv die gleiche Geschwindigkeit die Raketengeschwindigkeit.
Alles was im Triebwerk ist . also die Gasteilchen, bewegt sich langsamer als die Rakete.
addiert man beide impulse zusammen hätte man den gesamt impuls den man mit der idealisierung ermittelt
also
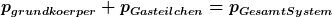
um den Impuls des Triebwerkinhalts zu ermitteln müsste man über alle Gasteilchen samt deren Massen und Geschwindigkeit addieren.
Das wollte ich mir natürlich nicht antun, geschweige denn das ich da überhaupt realistisch fortfahren könnte.
Ich habe einfach eine gemittelte Geschindigkeit genommen und zwar die Austrittsgeschwindigkeit des Gases durch die Hälfte mal der ungefähren Gasmasse.
Die Gasmasse habe ich damals glaube ich über den Druck und die Temperatur ungefähr abgeschätzt mit den Dimensionsangaben des Triebwerks bei der Saturn V, leider finde ich den Zettel nicht mehr
 )
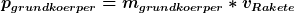
)
*v_{Raktengleichung}=(m_{grundkoerper}+m_{Gasmasse}) *v_{Rakete}-m_{Gasmasse}*v_{g}*0,5))

Der geringen Gasmasse stand dann die unglaubliche Startmasse der Saturn von 2900 tonnen gegenüber  davon 2500 tonnen Treibstoff. davon 2500 tonnen Treibstoff.
gegen Ende wird halt der Fehler größer aber es sind trotzdem noch immer 400 Tonnen, sodass mir bewusst wurde das der Fehler peanuts ist.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 05. März 2018 21:44 Titel: Thermodynamik Systemdynamiker Verfasst am: 05. März 2018 21:44 Titel: Thermodynamik |
 |
|
Die Ausströmgeschwindigkeit der Gase sind das Ergebnis eines thermodynamischen Prozesses. Deshalb ist diese Geschwindigkeit relativ zur Rakete im Vakuum zeitlich recht konstant und so gross wie möglich (in der Luft wirkt der Luftdruck dem Ausströmen der Gase entgegen). Diese Ausströmgeschwindigkeit heisst in der Literatur etwas irreführend spezifischer Impuls. Das ist die eine Geschichte.
Die zweite Geschichte ist die Berechnung der Beschleunigung der Rakete. Und da spielt es eine sehr grosse Rolle, dass die Masse abnimmt (deshalb die Booster). Die Beschleunigung der Rakete rechnet man über eine Impulsbilanz und eine Massenbilanz und meist im Bezugssytem Erde. So kann man auch komplexere Raketen rechnen, bei denen z. B. das Gas im Haupttriebwerk nicht gleich schnell austritt wie bei den Boostern.
_________________
Herzliche Grüsse Werner Maurer |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 06. März 2018 03:03 Titel: VeryApe Verfasst am: 06. März 2018 03:03 Titel: |
 |
|
Auto und Stein ruhen zu Beginn.
Nach der Federentspannung bewegen sich Auto und Stein voneinander weg.
reibverlustfrei.
| Beschreibung: |
|
| Dateigröße: |
18.87 KB |
| Angeschaut: |
6444 mal |
|
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 06. März 2018 07:56 Titel: TomS Verfasst am: 06. März 2018 07:56 Titel: |
 |
|
Ich sehe, worauf du hinauswillst.
Was du hier bestimmst ist - richtigerweise - die Relativgeschwindigkeit. Was aber oben gefragt ist, ist die Ausströmgeschwindigkeit. M.M.n. müsstest du einen Grenzübergang für infinitesimale Masse durchführen, denn genau dafür gilt die infinitesimale Form der Raketengleichung mit konstanter Ausströmgeschwindigkeit. Die potentielle Energie des Treibstoffs skaliert dabei linear mit der Masse (was in der Praxis natürlich nicht korrekt ist; das Triebwerk kann sicher nicht mit beliebig kleiner Massenzufuhr arbeiten).
Jedenfalls wirst du mit einem einfachen Mdell wieder bei der bekannten Raketengleichung landen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 06. März 2018 09:57 Titel: VeryApe Verfasst am: 06. März 2018 09:57 Titel: |
 |
|
| Zitat: | | Was du hier bestimmst ist - richtigerweise - die Relativgeschwindigkeit. Was aber oben gefragt ist, ist die Ausströmgeschwindigkeit. |
Der Stein wird innerhalb des Wagens beschleunigt und ist fertig beschleunigt wenn er den Wagen verlässt und die relativ Geschwindigkeit ist daher die beobachtete Austrittsgeschwindigkeit des Beobachters der sich im Wagen befindet.
Oder soll ich relativistische Effekte berücksichtigen?
| Zitat: | M.M.n. müsstest du einen Grenzübergang für infinitesimale Masse durchführen, denn genau dafür gilt die infinitesimale Form der Raketengleichung mit konstanter Ausströmgeschwindigkeit. Die potentielle Energie des Treibstoffs skaliert dabei linear mit der Masse (was in der Praxis natürlich nicht korrekt ist; das Triebwerk kann sicher nicht mit beliebig kleiner Massenzufuhr arbeiten).
|
was ich gemacht habe ist folgendes. Ich habe die Federkraft konstant wirken lassen, zeitliche Verläufe ermittelt und dann versucht das ganze aus den Beschleunigten Bezugssystem zu beschreiben und gesehen das man dort für die vergrößerte Austrittsgeschwindigkeit die nun zusätzlich Trägheitskraft verantwortlich machen kann, neben der federenergie die im dem Bezugssystem völlig auf den Stein übergeht.
Und diese wirkt auch in der Rakete, das waren meine Schlussflogerung.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Duke711
Anmeldungsdatum: 26.01.2017
Beiträge: 434
|
 Duke711 Verfasst am: 06. März 2018 14:55 Titel: Duke711 Verfasst am: 06. März 2018 14:55 Titel: |
 |
|
Ist das nicht Haarspalterei?
Alleine der Verbrennungsprozess ist doch alles andere als stationär und somit kann niemals die Ausströmungsgeschwindigkeit konstant sein.
Es ist doch offensichtlich das die Raketengleichung ein sehr vereinfachtes Modell ist und auch keine Massenträgheiten der Gasmolekühle berücksichtig werden.
ABer gut ich will eure eifrige Diskussion nicht weiter stören.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 06. März 2018 18:04 Titel: VeryApe Verfasst am: 06. März 2018 18:04 Titel: |
 |
|
das stimmt natürlich, aber trotzdem ist es interessant zu sehen, wo etwaige Abweichungen auftreten und deren Fehler ungefähr abzuschätzen zumindest für mich und schlussendlich will man es auch theoretisch genau verstehen.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 06. März 2018 18:11 Titel: DrStupid Verfasst am: 06. März 2018 18:11 Titel: |
 |
|
| Duke711 hat Folgendes geschrieben: | | Ist das nicht Haarspalterei? |
Natürlich ist das Haarspalterei. Es geht hier nur ums Prinzip. Praktisch ist das nicht relevant.
Um einen signifikanten Effekt zu erziehlen, muss man extreme Bedingungen wählen. Mit einer Ausströmgeschwindigkeit von Null habe ich bereits ein Beispiel genannt.
Eine andere Möglichkeit besteht darin, die Rakete auf einen Neutronenstern zu stellen und für einen Moment zu vergessen dass sie dabei so platt gedrückt wird wie Blattgold. In dem Fall würde die Gravitation den Treibstoff mit irrwitziger Geschwindigkeit aus dem Triebwerk saugen. Aus dem Einsteinschen Äquivalenzprinzip folgt dann, dass eine hinreichend starke Beschleunigung der Rakete den gleichen Effekt hätte.
Das Beispiel macht auch deutlich, warum die Wechselwirkungskräfte ebenfalls betroffen wären. Wenn der Treibstoff so schnell aus der Brennkammer strömt, dass er - wenn überhaupt - erst außerhalb der Rakete verbrennt, dann kann der Schub natürlich nicht mehr derselbe sein wie auf dem Teststand.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 06. März 2018 18:20 Titel: TomS Verfasst am: 06. März 2018 18:20 Titel: |
 |
|
| Duke711 hat Folgendes geschrieben: | Ist das nicht Haarspalterei?
Alleine der Verbrennungsprozess ist doch alles andere als stationär und somit kann niemals die Ausströmungsgeschwindigkeit konstant sein. |
Jein!
Zunächst mal ist klar, dass es sich bei der Ausströmgeschwindigkeit immer um eine effektive und gemittelte Geschwindigkeit handelt. Das setzen alle Beteiligten hier implizit voraus.
Dann ist klar, dass die Systemgrenze und damit diese Ausströmgeschwindigkeit an einem Punkt definiert werden muss, an dem das Gas dynamisch von der Rakete entkoppelt ist und damit keinen Rückstoß mehr übertragen kann. Ab diesem Punkt ist sicher eine rein kinematische Betrachtung möglich (oder umgekehrt: wenn keine rein kinematische Betrachtung möglich ist, dann ist die Systemgrenze nicht geeignet gewählt).
Was ich oben bereits angemerkt habe ist, dass die Ausströmgeschwindigkeit relativ bezüglich eines zu einem festen Zeitpunkt mitbewegten Inertialsystems = bezüglich “dem zu genau diesem Zeitpunkt gültigen Ruhesystem” definiert ist. Damit kann diese Ausströmgeschwindigkeit nicht explizit (!) von der Geschwindigkeit der Rakete bzgl. des ursprünglichen Ruhesystems = der Startrampe abhängen, denn dies würde die Galilei-Invarianz verletzen.
Bis hierher sollte Einigkeit herrschen.
Die verbleibende Frage ist, ob die so definierte Ausströmgeschwindigkeit noch von der aktuellen Beschleunigung, damit von der aktuellen Masse und somit implizit (!) doch von der Geschwindigkeit abhängig sein kann. Wohlgemerkt darf es sich dabei nicht um eine andere Definition dieser Ausströmgeschwindigkeit handeln.
M.E. ist das zwar nicht von praktischer jedoch durchaus grundsätzlicher Bedeutung.
Der o.g. Ansatz mit der Feder geht schon in die richtige Richtung, allerdings muss man m.E. einige Modifikationen vornehmen. Zum einen ist die potentielle Energie der Masse m nicht einfach in einer Feder gespeichert, sondern die potentielle Energie der infinitesimalen (!) Masse dm ist in einer Feder genau dieser Masse dm gespeichert. Aus diesem Ansatz muss man zunächst die infinitesimale Variante der Raketengleichung mit konstanter “Ausströmgeschwindigkeit” rekonstruieren können, sonst wäre der ganze Ansatz offensichtlich inkonsistent.
Anschließend kann man sich überlegen diesen Ansatz um dynamische Effekte zu erweitern, aus denen sich Korrekturen der zuvor berechneten “Ausströmgeschwindigkeit” ergeben.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 06. März 2018 23:58 Titel: TomS Verfasst am: 06. März 2018 23:58 Titel: |
 |
|
Zur Idee von VeryApe sowie zu meiner Anmerkung
| TomS hat Folgendes geschrieben: | | m.M.n. müsstest du einen Grenzübergang für infinitesimale Masse durchführen, denn genau dafür gilt die infinitesimale Form der Raketengleichung mit konstanter Ausströmgeschwindigkeit. Die potentielle Energie des Treibstoffs skaliert dabei linear mit der Masse. |
hier ein einfaches Beispiel: Gegeben seinen reibungsfrei über den Boden gleitender Schlitten der Masse M auf dem eine Kugel der Masse m entlang eine Kurve mit dem Profil h(x-l) mit
 < 0)
herunterrollt. Dabei betrachten wir zunächst nur den Abschnitt
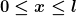
Über diesen Abschnitt wird die Kugel also zu positivem x hin beschleunigt.
Die Energie dies Gesamtsystems aus Schlitten mit Masse M und Geschwindigkeit v sowie Kugel mit Masse m und Geschwindigkeit u lautet demnach
 \stackrel{!}{=} \text{const.})
Für die Impulserhaltung gilt
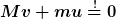
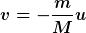
Einsetzen des Potentials der Kugel und Anwenden des Energiesatzes liefert
|_{x=0} \stackrel{!}{=} mg\,h_0 = \frac{M}{2}v^2 + \frac{m}{2}u^2 + mg\,h(x-l))
Mittels Einsetzen des Ergebnisses aus dem Impulssatz folgt
] = \left(1 + \frac{m}{M}\right) u^2(x))
und damit die Geschwindigkeit u(x) als Funktion von x.
Es sei nun
|_{x \ge l} = 0)
und somit
 u_l^2)
also
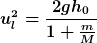
Letzteres entspricht der Geschwindigkeit, mit der die Kugel die Bahn verlässt und die sie für x > l beibehält; insbs. überträgt die Kugel keinen Rückstoß mehr auf den Schlitten.
Dies ist unser extrem vereinfachtes Modell für die Düse der Rakete!
Die Herleitung erfolgte im Ruhesystem des Schlittens zum Zeitpunkt des Losrollens der kleinen Kugel. Natürlich ist diese Betrachtung invariantnunte Galilei-Transformation.
Für die Verwendung in der Raketengleichung
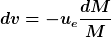
ist dieses Modell noch etwas anzupassen. Es gilt nämlich zunächst
 = \frac{2gh_0}{1 + \frac{m}{M(v)}})
für die geschwindigkeitsabhängige Masse M(v) des Schlittens bzw. der Rakete.
Allerdings wird hier immer nur eine infinitesimale Masse dm ausgestoßen, d.h. wir setzen
 = \frac{2gh_0}{1 + \frac{dm}{M(v)}} = 2gh_0 + \mathcal{O}\left(\frac{dm}{M(v)}\right))
Einsetzen dieser Geschwindigkeit in die Raketengleichung liefert
 \right] \frac{dM}{M} )
Damit sind die kinematischen Korrekturen, die sich aufgrund der Reduzierung der Masse M(v) für die Austrittsgeschwindigkeit u(v) ergeben in der Differentialgleichung von zweiter Ordnung und dürfen zu Null gesetzt werden.
Die Raketengleichung ist demnach in dieser Hinsicht exakt, es resultieren keine kinematischen Korrekturen!
| VeryApe hat Folgendes geschrieben: | | ... trotzdem ist es interessant zu sehen, wo etwaige Abweichungen auftreten und deren Fehler ungefähr abzuschätzen zumindest für mich und schlussendlich will man es auch theoretisch genau verstehen. |
Der Ansatz von VeryApe war hilfreich, nur leider noch nicht vollständig. Es fehlte die Überlegung, dass die ausgestoßene Masse und demnach die in den Gleichungen auftretende potentielle Energie dieser Masse infinitesimal ist und in der Differentialgleichung letztlich nicht beiträgt.
Zuletzt bearbeitet von TomS am 07. März 2018 00:43, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 07. März 2018 00:19 Titel: TomS Verfasst am: 07. März 2018 00:19 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Um einen signifikanten Effekt zu erziehlen, muss man extreme Bedingungen wählen. Mit einer Ausströmgeschwindigkeit von Null habe ich bereits ein Beispiel genannt. |
Ich denke, ich habe gezeigt, dass keine kinematischen Korrekturen vorliegen.
| DrStupid hat Folgendes geschrieben: | | Eine andere Möglichkeit besteht darin, die Rakete auf einen Neutronenstern zu stellen ... In dem Fall würde die Gravitation den Treibstoff mit irrwitziger Geschwindigkeit aus dem Triebwerk saugen. |
Das ist in diesem Beispwohl irrelevant; die Gravitation hatten wir ohnehin nicht berücksichtigt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 07. März 2018 02:09 Titel: VeryApe Verfasst am: 07. März 2018 02:09 Titel: |
 |
|
| toms hat Folgendes geschrieben: | | Ich denke, ich habe gezeigt, dass keine kinematischen Korrekturen vorliegen |
Meiner Meinung nach hast du hier gezeigt, das für die Idealisierung des Triebwerks also Triebwerk hat keine Ausdehnung, keine Korrekturen notwendig sind.
Das hätten dir aber vorher so ziemlich alle bestätigt.
Du berücksichtigst meiner Meinung nach nicht das das dm Teilchen eine endliche zeit braucht bis es die Wegstrecke herunterfällt und somit auch der Schlitten schon einen endlichen Zuwachs an Geschwindigkeit erfahren hat.
das habe ich einige Beiträge vorher schon geschrieben.
Du schreibst die Berechnung geht vom Ruhsystem des Schlittens aus.
Also das Inertialsystem das vom Beginn mit dem Schlitten ruht.
Bis die Kugel in der endlichen Zeit nach unten durchmarschiert ist hat der Schlitten auf dieses Ruhsystem schon einen endlichen Geschwindigkeitszuwachs erfahren, weil zuvor schon etliche anderen dm Kugeln durchmarschiert sind, weil sonst macht ja das keinen Sinn wenn da nicht die ganze Zeit ein dm pro dt herauskommt.
Von diesem Geschwindigkeitszuwachs sehe ich nichts bei dir, da sehe ich nur ul auf dieses Ruhsystem.
Wo ist die Geschwindigkeit des Schlittens auf dieses Ruhsystem bis das Teilchen unten angekommen ist?=
und wie ist dann die realtive Geschwindigkeit auf den Schlitten.
In der Raktengleichung arbeitet man mit der Austrittsgeschwindigkeit auf den Schlitten was der relativen Geschwindigkeit, deines Ruhinertialsystems zwischen Schlitten und Kugel entspricht.
Vielleicht sehe ich da was falsch.
Aber momentan blicke ich da nicht so durch was du da beweisen willsd.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 07. März 2018 08:49 Titel: TomS Verfasst am: 07. März 2018 08:49 Titel: |
 |
|
Zunächst mal sollten wir uns darauf einigen, dass meine (eigtl. sogar deine :-) Herleitung völlig korrekt ist – oder dass du mir explizit einen Fehler zeigst.
| VeryApe hat Folgendes geschrieben: | | toms hat Folgendes geschrieben: | | Ich denke, ich habe gezeigt, dass keine kinematischen Korrekturen vorliegen |
Meiner Meinung nach hast du hier gezeigt, dass für die Idealisierung des Triebwerks also Triebwerk hat keine Ausdehnung, keine Korrekturen notwendig sind.
Das hätten dir aber vorher so ziemlich alle bestätigt.
Du berücksichtigst meiner Meinung nach nicht, dass das dm Teilchen eine endliche Zeit braucht bis es die Wegstrecke herunterfällt und somit auch der Schlitten schon einen endlichen Zuwachs an Geschwindigkeit erfahren hat.
|
Das berücksichtige ich ganz explizit in meiner Herleitung; deswegen führe ich das Potential ein, und deswegen leite ich die Gleichung
] = \left(1 + \frac{m}{M}\right) u^2(x))
mit der Geschwindigkeit u(x) als Funktion von x ab.
Darin steckt später die Abhängigkeit der Geschwindigkeit der Masse dm vom Ort x innerhalb des Triebwerks.
Wie ich aber zuvor geschrieben habe, „[ist] die Systemgrenze und damit diese Ausströmgeschwindigkeit an einem Punkt definiert …, an dem das Gas dynamisch von der Rakete entkoppelt ist und damit keinen Rückstoß mehr übertragen kann. Ab diesem Punkt ist sicher eine rein kinematische Betrachtung möglich (oder umgekehrt: wenn keine rein kinematische Betrachtung möglich ist, dann ist die Systemgrenze nicht geeignet gewählt)“.
Dies ist in meinem Modell der Punkt x = l. D.h. für x < l hat noch keine dynamische Entkopplung stattgefunden, daher ist dieser Bereich im Folgenden irrelevant.
| VeryApe hat Folgendes geschrieben: | Du schreibst die Berechnung geht vom Ruhsystem des Schlittens aus. Also das Inertialsystem das vom Beginn mit dem Schlitten ruht.
Bis die Kugel in der endlichen Zeit nach unten durchmarschiert ist hat der Schlitten auf dieses Ruhsystem schon einen endlichen Geschwindigkeitszuwachs erfahren, weil zuvor schon etliche anderen dm Kugeln durchmarschiert sind …
Von diesem Geschwindigkeitszuwachs sehe ich nichts bei dir, da sehe ich nur ul auf dieses Ruhesystem. |
Auch das berücksichtige ich durch den Korrekturterm erster Ordnung in
 = \frac{2gh_0}{1 + \frac{m}{M(v)}})
sowie
 \right] \frac{dM}{M} )
Allerdings ist dieser Effekt aufgrund der infinitesimalen Masse dm von zweiter Ordnung; daher folgen keine Korrekturen der Differentialgleichung.
| VeryApe hat Folgendes geschrieben: | | Wo ist die Geschwindigkeit des Schlittens auf dieses Ruhsystem bis das Teilchen unten angekommen ist? |
Habe ich nicht explizit hingeschrieben, aber das folgt logischerweise aus
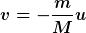
Wie ich aber zuvor geschrieben habe, „[wird] die Ausströmgeschwindigkeit relativ bezüglich eines zu einem festen Zeitpunkt mitbewegten Inertialsystems definiert“; ich verwende dazu das Inertialsystem, das beim Losrollen der Kugel gilt, nicht das Inertialsystem, das nach der Beschleunigungsphase gültig wäre.
Allerdings ist der Geschwindigkeitsunterschied
}u)
zwischen beiden Systemen wiederum infinitesimal, in der Raketengleichung von zweiter Ordnung und damit irrelevant.
| VeryApe hat Folgendes geschrieben: | | … und wie ist dann die relative Geschwindigkeit auf den Schlitten. |
Nun, genau wie bei dir. Allerdings ist das aus den o.g. Gründen irrelevant.
| VeryApe hat Folgendes geschrieben: | | Vielleicht sehe ich da was falsch. |
Nein, du siehst letztlich gar nichts falsch. Meiner Herleitung entspricht zunächst deiner, allerdings berücksichtige ich zudem, dass die potentielle Energie proportional zur Masse des ausgestoßenen Treibstoffs ist, was ich durch die kleine Kugel und das Potential modelliere, und ich berücksichtige bei der endgültigen Ableitung der Raketengleichung, dass Terme zweiter Ordnung nicht beitragen.
| VeryApe hat Folgendes geschrieben: | | Aber momentan blicke ich da nicht so durch was du da beweisen willst. |
Ich will zeigen, dass man eure Anmerkungen berücksichtigen kann, dass sie jedoch in der Raketengleichung selbst zu keinen Korrekturtermen führen, dass diese also gültig bleibt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 07. März 2018 08:55 Titel: TomS Verfasst am: 07. März 2018 08:55 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | Meiner Meinung nach hast du hier gezeigt, dass für die Idealisierung des Triebwerks [ohne] Ausdehnung, keine Korrekturen notwendig sind.
…
Bis die Kugel … nach unten durchmarschiert ist, hat der Schlitten auf dieses Ruhsystem schon einen endlichen Geschwindigkeitszuwachs erfahren, weil zuvor schon etliche anderen dm Kugeln durchmarschiert sind
…
Von diesem Geschwindigkeitszuwachs sehe ich nichts bei dir … |
OK, das ist ein Einwand, den ich auf den zweiten Blick doch nicht ignorieren möchte.
Es ginge also darum, ein dynamisches Modell zu entwickeln, in dem man endlich viele Kugeln betrachtet, die in einem zeitlichen Abstand dt losrollen, was zu einem endlichen Abstand der Kugeln untereinander führt. Im Grenzfall dt = 0 füllen diese das abschüssige Potential dicht aus.
Ja, ich schau‘ mir diese Erweiterung des Modells mal an.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Portisch
Gast
|
 Portisch Verfasst am: 07. März 2018 09:02 Titel: Portisch Verfasst am: 07. März 2018 09:02 Titel: |
 |
|
Kannsd du mir nur kurz erklären was dieses Zeichen bedeutet 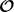
|
|
 |
|
|


















 davon 2500 tonnen Treibstoff.
davon 2500 tonnen Treibstoff.
