| Autor |
Nachricht |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 16. Jan 2008 21:11 Titel: Schwerpunkt eines Zylinders Mulder Verfasst am: 16. Jan 2008 21:11 Titel: Schwerpunkt eines Zylinders |
 |
|
Hallo,
wir sollen Trägheitsmoment und Schwerpunkt eines Vollzylinders mit dem Radius R und der Höhe H bestimmen. Das Trägheitsmoment haben wir, aber beim Schwerpunkt haben wir ein Problem.
Die Dichte nimmt mit zunehmender Höhe zu:
=\rho_0) und und =2\rho_0 )
Die beiden Werte sind gegeben, die Dichte nimmt also mit zunehmender Höhe linear zu. Kann man also bestimmt irgendwie mit Integration bestimmen. Leider fehlt uns die Formel, die wir dafür benötigen.
Kann uns da jemand ein wenig weiter helfen? 
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 16. Jan 2008 23:38 Titel: dermarkus Verfasst am: 16. Jan 2008 23:38 Titel: |
 |
|
Kennt ihr schon die Formel für den Schwerpunkt, wenn es sich um den Schwerpunkt mehrerer Massenpunkte handelt? Also so etwas:
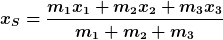
?
Und wollt ihr mal versuchen, daraus zu schließen, wie so eine Formel als Integral aussieht, wenn es sich statt dessen um viele infinitesimal dünne Massestückchen handelt, die da, mit ihrer Position multipliziert, im Zähler addiert werden?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 01:20 Titel: Mulder Verfasst am: 17. Jan 2008 01:20 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | | Und wollt ihr mal versuchen, daraus zu schließen, wie so eine Formel als Integral aussieht [...] ? |
Genau da liegt nämlich das Problem... 
Wie mag das aussehen? Also, die Dichte nimmt linear zu, also inegriert man eventuell über eine Gerade, wenn man so will?
Der Schwerpunkt wäre ja 
(hattest du ja schon geschrieben...)
Sorry, ich weiß es wirklich nicht... ich würde irgendwas quadratisches erwarten, aber wie genau ich das angehen müsste... und vor allem, was ich mit dem Bruch machen müsste, weiß ich wirklich nicht. 
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 01:27 Titel: dermarkus Verfasst am: 17. Jan 2008 01:27 Titel: |
 |
|
Das Summenzeichen ist schonmal der erste Fortschritt 
Im Nenner steht ja nun nichts anderes als die Summe aller einzelnen Massen, das ist ja die Gesamtmasse M. Damit hätten wir also schonmal
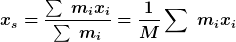
Nun bleibt also nur noch, die Summe in ein Integral umzuwandeln. Dazu zerschneiden wir den Zylinder mal in Stückchen der Dicke 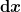
Wie groß ist dann die Masse ) eines solchen Scheibchens, wenn du die Querschnittsfläche des Zylinders und seine Massendichte in Abhängigkeit von der Höhe eines solchen Scheibchens, wenn du die Querschnittsfläche des Zylinders und seine Massendichte in Abhängigkeit von der Höhe  kennst? kennst?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 02:29 Titel: Mulder Verfasst am: 17. Jan 2008 02:29 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | Wie groß ist dann die Masse ) eines solchen Scheibchens, wenn du die Querschnittsfläche des Zylinders und seine Massendichte in Abhängigkeit von der Höhe eines solchen Scheibchens, wenn du die Querschnittsfläche des Zylinders und seine Massendichte in Abhängigkeit von der Höhe  kennst? kennst? |
Also... Die Querschnittsfläche mit  kennt man ja. Könnte man dies ebenfalls vor das Integral ziehen? Das ändert sich ja mit H nicht. kennt man ja. Könnte man dies ebenfalls vor das Integral ziehen? Das ändert sich ja mit H nicht.
Allerdings nage ich immer noch an dem ) ... ...
Wenn ich mir das grafisch (Steigungsdreickk, wenn man so will) anschaue, gehe ich ja, wenn ich "um H nach rechts" gehe, um 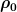 nach oben. nach oben.
Da würde ich sagen, dass die Dichte abhängig von H dann so aussieht: =x+x_0)
Oh weh... ich mache es mir bestimmt wieder viel komplizierter, als es eigentlich ist...
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 10:32 Titel: dermarkus Verfasst am: 17. Jan 2008 10:32 Titel: |
 |
|
Du bist genau auf der richtigen Spur 
Als nächstes geht es in der Tat darum, die Funktionsgleichung für das ) aufzustellen. Und zwar so, dass aufzustellen. Und zwar so, dass
=\rho_0) und und =2\rho_0 )
ist und dass die Funktionsgleichung zwischen diesen beiden Punkten eine Gerade ist.
Erfüllt dein bisheriges ) diese Bedingungen? Falls nein, versuch mal, es solange zu verändern, bis es passt! diese Bedingungen? Falls nein, versuch mal, es solange zu verändern, bis es passt!
Oder lies an deiner Skizze die Geradengleichung für das ) ab: Was genau ist der y-Achsenabschnitt der Geraden, und was genau ist ihre Steigung, die du an deinem Steigungsdreieck abliest? ab: Was genau ist der y-Achsenabschnitt der Geraden, und was genau ist ihre Steigung, die du an deinem Steigungsdreieck abliest?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 17:09 Titel: dermarkus Verfasst am: 17. Jan 2008 17:09 Titel: |
 |
|
Einverstanden 
Wie lautet damit die Masse ) so einer herausgeschnittenen Scheibe? Und was steht damit also insgesamt in unserer Formel für so einer herausgeschnittenen Scheibe? Und was steht damit also insgesamt in unserer Formel für 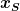 ? ?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 17:14 Titel: Mulder Verfasst am: 17. Jan 2008 17:14 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | Einverstanden 
Wie lautet damit die Masse ) so einer herausgeschnittenen Scheibe? so einer herausgeschnittenen Scheibe?
Und was steht damit also insgesamt in unserer Formel für 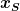 ? ? |
=A (\frac{\rho_0}{H} x + \rho_0))
Ich muss nun über das ) integrieren? Der Rest kann doch vor das Integral, oder? integrieren? Der Rest kann doch vor das Integral, oder?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 17:22 Titel: dermarkus Verfasst am: 17. Jan 2008 17:22 Titel: |
 |
|
| Mulder hat Folgendes geschrieben: |
=A (\frac{\rho_0}{H} x + \rho_0))
|
Das stimmt noch nicht ganz, da fehlt noch die Dicke (= Höhe) der Scheibe.
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 17:25 Titel: Mulder Verfasst am: 17. Jan 2008 17:25 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | | Das stimmt noch nicht ganz, da fehlt noch die Dicke (= Höhe) der Scheibe. |
Die ist doch dx, oder nicht? Also darüber integrieren?
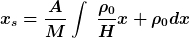
So etwa? 
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 17:27 Titel: dermarkus Verfasst am: 17. Jan 2008 17:27 Titel: |
 |
|
Ja, die ist dx. Aber nicht so schnell, schreib das erst einmal sauber in unsere Formel, bevor du anfängst, dir dann zu überlegen, was das dann für ein Integral ergibt, und über was dann da integriert werden muss.
Also mit allen erforderlichen Klammern, und erst noch mal mit dem Summenzeichen von oben.
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 17:29 Titel: Mulder Verfasst am: 17. Jan 2008 17:29 Titel: |
 |
|
=(Adx) (\frac{\rho_0}{H} x + \rho_0))
Irgendwie bescheuert.... 
Edit: Ach so, mit Summenzeichen... Moment!
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 17:36 Titel: Mulder Verfasst am: 17. Jan 2008 17:36 Titel: |
 |
|
Wäre das dann sowas hier:
)x_i))
?
Irgendwie weiß ich jetzt wieder nicht, was ich mit dem "x" aus der Formel für die Masse machen soll...
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 17:40 Titel: dermarkus Verfasst am: 17. Jan 2008 17:40 Titel: |
 |
|
| Mulder hat Folgendes geschrieben: |
)x_i))
|
Schau mal genau hin, du hast noch was vergessen 
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 17:42 Titel: Mulder Verfasst am: 17. Jan 2008 17:42 Titel: |
 |
|
Ach so... die Dicke wieder? dx?
(\frac{\rho_0}{H}x_i+\rho_0))x_i))
So?
Oder immer noch falsch?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 17:50 Titel: dermarkus Verfasst am: 17. Jan 2008 17:50 Titel: |
 |
|
| Mulder hat Folgendes geschrieben: | Ach so... die Dicke wieder? dx?
(\frac{\rho_0}{H}x_i+\rho_0))x_i))
|
Einverstanden, jetzt haben wir alles beieinander 
Magst du nun am besten die Faktoren, die da stehen, so ordnen, dass das 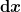 ganz hinten steht? ganz hinten steht?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 17:52 Titel: Mulder Verfasst am: 17. Jan 2008 17:52 Titel: |
 |
|
Hmm?
(\frac{\rho_0}{H}x_i+\rho_0))x_i)dx)
So, oder was?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 17:57 Titel: dermarkus Verfasst am: 17. Jan 2008 17:57 Titel: |
 |
|
Einverstanden  Damit haben wir nun Damit haben wir nun
\cdot x)=\frac{1}{M}\sum~\left (A(\frac{\rho_0}{H}x_i+\rho_0)x \right ) \dd x)
denn die Position unseres Massenscheibchens heißt ja nun einfach  und nicht mehr und nicht mehr 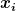 wie vorher bei den durchnummerierten wie vorher bei den durchnummerierten 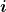 Stückchen. Stückchen.
Siehst du nun, welchem Integral diese Summe aus infinitesimalen Stückchen \cdot x)) entspricht? entspricht?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 18:02 Titel: Mulder Verfasst am: 17. Jan 2008 18:02 Titel: |
 |
|
Wäre das dann einfach 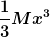 ? ?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 18:04 Titel: dermarkus Verfasst am: 17. Jan 2008 18:04 Titel: |
 |
|
|
Das weiß ich noch nicht, so weit können wir doch jetzt noch gar nicht rechnen. Wir sind doch gerade noch dabei, aus der Summe ein Integral zu machen, oder?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 18:11 Titel: Mulder Verfasst am: 17. Jan 2008 18:11 Titel: |
 |
|
|
Tut mir leid, dann muss ich passen... wie ich das in ein Integral verwandle, will nicht in meinen Schädel.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 18:21 Titel: dermarkus Verfasst am: 17. Jan 2008 18:21 Titel: |
 |
|
Erinnerst du dich noch an den Matheunterricht aus der 11. Klasse? Ein Integral ist ja nichts anderes als die Summe infinitesimaler Stückchen. Also:
x \right ) \dd x= \frac{1}{M} \int~\left (A(\frac{\rho_0}{H}x_i+\rho_0)x \right ) \dd x)
Magst du dazu noch die passenden Integralgrenzen ergänzen?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 21:03 Titel: Mulder Verfasst am: 17. Jan 2008 21:03 Titel: |
 |
|
Hmmm... man integriert doch von 0 bis H, oder? Über den ganzen Zylinder...
x \right ) \dd x)
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2008 21:09 Titel: dermarkus Verfasst am: 17. Jan 2008 21:09 Titel: |
 |
|
Einverstanden 
Entschuldige übrigens, dass ich in der Gleichung manchmal fälschlicherweise noch 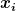 geschrieben hatte, das soll natürlich da auch schon geschrieben hatte, das soll natürlich da auch schon  heißen. heißen.
Weißt du auch schon, was die Integrationsvariable in diesem Integral ist? Und kannst du damit das Integral schon komplett ausrechnen?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 17. Jan 2008 23:50 Titel: Mulder Verfasst am: 17. Jan 2008 23:50 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | Entschuldige übrigens, dass ich in der Gleichung manchmal fälschlicherweise noch 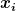 geschrieben hatte, das soll natürlich da auch schon geschrieben hatte, das soll natürlich da auch schon  heißen. heißen. |
Nun gut, das lasse ich ganz ausnahmsweise nochmal durchgehen.  
Okay, Scherz beiseite...
| dermarkus hat Folgendes geschrieben: | | Weißt du auch schon, was die Integrationsvariable in diesem Integral ist? Und kannst du damit das Integral schon komplett ausrechnen? |
Da hänge ich noch ein wenig. Die Frage ist ja, was ich davon noch davor ziehen kann. Und ziemlich ungemütlich finde ich auch das x in der Klammer. Einfches ausmultiplizieren bringt da irgendwie herzlich wenig.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2008 00:12 Titel: dermarkus Verfasst am: 18. Jan 2008 00:12 Titel: |
 |
|
Welche Variable läuft denn da von 0 bis H ?
x \right ) \dd x)
Das im Integral mal auszumultiplizieren, ist sicher kein schlechter Schritt auf dem Weg, dieses Integral auszurechnen 
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 18. Jan 2008 01:36 Titel: Mulder Verfasst am: 18. Jan 2008 01:36 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | | Welche Variable läuft denn da von 0 bis H ? |
Die Höhe x.
| dermarkus hat Folgendes geschrieben: | | Das im Integral mal auszumultiplizieren, ist sicher kein schlechter Schritt auf dem Weg, dieses Integral auszurechnen |
Nein? Ist ja hässlich... nun gut, dann wäre ich jetzt an diesem Punkt:
dx)
In Ordnung?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2008 01:38 Titel: dermarkus Verfasst am: 18. Jan 2008 01:38 Titel: |
 |
|
Ja  Nur weiter so Nur weiter so 
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 18. Jan 2008 01:43 Titel: Mulder Verfasst am: 18. Jan 2008 01:43 Titel: |
 |
|
Hmm... okay, wenn ich das dann einfach mal so integriere, erhalte ich nach dem ganzen zusammenfassen (wenn ich den Rechenschritt noch aufschreiben soll, dann lass es mich wissen):

Einwände?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2008 01:48 Titel: dermarkus Verfasst am: 18. Jan 2008 01:48 Titel: |
 |
|
Keine 
Nun bleibt nur noch, das M auszurechnen.
Kannst du dafür auf ganz ähnliche Weise ein Integral aufstellen?
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 18. Jan 2008 01:53 Titel: Mulder Verfasst am: 18. Jan 2008 01:53 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | | Kannst du dafür auf ganz ähnliche Weise ein Integral aufstellen? |
Nimmt das denn gar kein Ende? 
Okay, versuchen wir es mal.
x) dx)
Geht das in Ordnung?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2008 02:03 Titel: dermarkus Verfasst am: 18. Jan 2008 02:03 Titel: |
 |
|
Was hast du da für die Masse m(x) eingesetzt? Magst du das nochmal mit dem vergleichen, was du oben schon mal hattest?
| Mulder hat Folgendes geschrieben: | =(Adx) (\frac{\rho_0}{H} x + \rho_0))
|
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 18. Jan 2008 02:06 Titel: Mulder Verfasst am: 18. Jan 2008 02:06 Titel: |
 |
|
Ups.... also so:
 dx)
Wenn ich das jetzt ganz stur einsetze.. vorhin hatten wir ja m(x)*x, und jetzt betrachten wir nur m(x), oder?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2008 02:09 Titel: dermarkus Verfasst am: 18. Jan 2008 02:09 Titel: |
 |
|
Genau 
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 18. Jan 2008 02:16 Titel: Mulder Verfasst am: 18. Jan 2008 02:16 Titel: |
 |
|
Also gut, dann integriere ich das einfach wieder auf.
Dann habe ich den ganzen Schmand zusammengefasst, vereinfacht, gekürzt und so weiter und nun bin ich bange, dass das jetzt wieder zu einfach wird, denn ich habe raus:
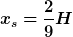
Das macht ja allein schon physikalisch gesehen keinen Sinn... wenn die Dichte zunimmt, sollte der Schwerpunkt weiter oben anzusiedeln sein.
Ich rechne es noch einmal durch...
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 18. Jan 2008 02:21 Titel: Mulder Verfasst am: 18. Jan 2008 02:21 Titel: |
 |
|
Quark... jetzt verrechne ich mich sogar schon bei (2/3) * (5/6)... 
Also, jetzt habe ich 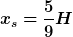
Das klingt plausibel, würde ich sagen...
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2008 02:26 Titel: dermarkus Verfasst am: 18. Jan 2008 02:26 Titel: |
 |
|
Einverstanden 
Damit haben wir also insgesamt nun erfolgreich eine Formel hergeleitet und verwendet, die folgende Form hatte:
 \cdot x \right) \dd x}{\int \left( A \varrho(x) \right) \dd x})
|
|
 |
Mulder

Anmeldungsdatum: 01.11.2007
Beiträge: 80
|
 Mulder Verfasst am: 18. Jan 2008 02:28 Titel: Mulder Verfasst am: 18. Jan 2008 02:28 Titel: |
 |
|
 )
Das meint jetzt die von der Höhe x abhängige Dichte, oder?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2008 02:38 Titel: dermarkus Verfasst am: 18. Jan 2008 02:38 Titel: |
 |
|
|
Ja. Die hast du oben mit deinem Diagramm aufgestellt.
|
|
 |
|