Schwerpunkt, Kreis mit Loch

pingu · Anmeldungsdatum: 30.06.2007 Beiträge: 94

Hallo zusammen!

Hab auch noch ne Frage zum Schwerpunkt. Bei dem angehängten Bild wird als Tipp gegeben,man könnte ihn aurechnen mit Hilfe dieser Formel :

etc (für ys genau dasselbe. Über ys kann ich ja schon sagen, das er sich auf der x-Achse befindet aufgrund der Symmetrie. Aber Ich hab ja das Volumen gar nicht, um dieses Integral auszurechnen:-(. Ich habs mal so versucht, dass ich für das Volumen einfach den Flächeninhalt dieser Figur nehme, und für x selbst -2R und 2R nehme, da sich das Koordinatensystem ja im Nullpunkt befindet.
Kann mir da jemand weiterhelfen?

Lg

dermarkus · Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788

Wenn du Volumenintegrale ausrechnen möchtest, dann darfst du gerne annehmen, das ganze habe in z-Richtung die Dicke d.

Magst du das mal konkret hinschreiben, und merkst du, dass sich dieses d dann am Ende rauskürzt, so dass statt den Volumina hier tatsächlich nur Flächen übrigbleiben?

---------------------------------

Wenn du ein bisschen genauer hinschaust, dann kannst du dir das Ausrechnen von Integralen hier sparen.

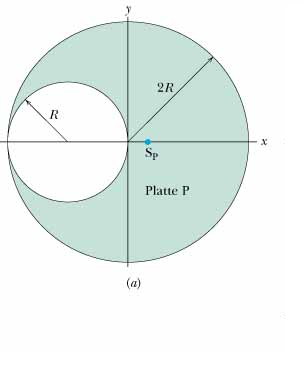
Siehst du in dieser Zeichnung Teilkörper, deren Schwerpunkt und deren Masse du bereits kennst? Erleichtert das deine Rechnung deutlich?

pingu · Anmeldungsdatum: 30.06.2007 Beiträge: 94

Ja, also man kann den Schwerpunkt das grossen (unausgeschnitten) Kreises ausrechnen, also aurechnen ist übertrieben, der befindet sich ja aufgrund der Symmetrie einfach im Mittelpunkt. Und dann könnte man noch den kleinen Kreis nehmen und dort den Schwerpunkt, also den Mittelpunkt, bestimmen.

. Für V kann ich ja schlecht wieder dasselbe wie unter dem Bruchstrich einsetzen, weil es sich ja sonst wegkürzen würde. Oder muss ich da noch Grenzen beachten?

lg

dermarkus · Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788

Wenn du die zwei Kreisscheiben hast, dann brauchst du gar keine Integrale mehr.

Magst du mal ein Koordinatensystem wählen und in diesem Koordinatensystem die Lage der beiden Schwerpunkte der beiden Kreise angeben? Und dann noch dazuschreiben, welche Massen du diesen beiden Kreisscheiben zuordnest?

pingu · Anmeldungsdatum: 30.06.2007 Beiträge: 94

Also ich würde das Koordinatensystem wie auf dem Bild in die Mitte des grossen Kreises legen. Also liegt der erste Schwerpunkt bei (0/0) und der zweite bei (-R/0). Und die Masse vom ersten ist (2R)²*pi*d*roh und die des zweiten (R)²*pi*d*roh. Aber ich kenn z.b. die Dichte gar nicht...

lg

dermarkus · Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788

Einverstanden smile

Die Dichte brauchst du nicht für die Bestimmung des Schwerpunktes, die kürzt sich dann am Ende wieder raus.

Kennst du nun eine Formel für den Schwerpunkt eines zusammengesetzten Körpers, deren Teilschwerpunkte und Teilmassen bekannt sind?

Wie würdest du in dieser Formel die Tatsache berücksichtigen, dass die kleine Kreisscheibe nicht dazukommt, sondern weggenommen wird?

pingu · Anmeldungsdatum: 30.06.2007 Beiträge: 94

Ja, kenne ich :-).

.

Gut, dann würd ich jetzt folgendes tun: m1 kann man ja wie gesagt auch durch roh*Volumen ausdrücken, wobei sich roh und auch d (Dicke) wegkürzt.
Somit setze ich für m1 = (2R)²*pi und für x1=0 ein. Somit fällt m1x1 schon mal weg. Weiter setzte ich für m2 = R²*pi und für x2=-R. Das ergibt für m2x2=-R³*pi. und das schliesslich noch durch m1+m2 teilen. Das ergibt dann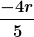

.

dermarkus · Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788

Das wäre die Rechnung, wenn die kleine Scheibe zusätzlich da wäre.

Nun ist die "kleine Scheibe" aber ja das, was in der großen Scheibe fehlt.

Wie könnte man das in dieser Rechnung berücksichtigen?

pingu · Anmeldungsdatum: 30.06.2007 Beiträge: 94

Hm ja, das ist ja dann die Masse, die verschwindet. Also dann müsste man unter dem Bruchstrich die grössere Masse minus die kleine rechnen, also m1 - m2. Und oben kommt meiner Meinung nach auch noch ein Minus hin, sodass es wieder ein + wird (0 - V2R*(-1)). Und das ergäbe dann (4R)/3. Stimmt das so?

lg

dermarkus · Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788

pingu · Anmeldungsdatum: 30.06.2007 Beiträge: 94

Ok, so:

.
Uuups, da hab ich mich wohl vorher verrechnet, denn eigntl hab ichs da genau gleich gemacht, nur ist dann dabei was falsches rausgekommen LOL Hammer

. Ist das jetzt so richtig?

lg

dermarkus · Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788

Einverstanden smile

pingu · Anmeldungsdatum: 30.06.2007 Beiträge: 94

Ah ok, sehr gut. Ja, dann hab ichs verstanden. Danke vielmals, du warst echt eine Hilfe :-). Kurze Frage noch zur anderen Ausrechnungsvariante. Es wird ja da nach dm integriert. Muss das m als Masse oder als Koordinate x,y aufgefasst werden? Und muss da noch was bei den Grenzen eingesetzt werden?

lg

dermarkus · Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788

Mit integrieren würde ich das nicht rechnen müssen wollen.

Denn die Aufgabe ist absichtlich so gestrickt, dass sie mit dem Zerlegen in unsere zwei Teilkreise sehr leicht geht, aber mit dem Integrieren zu schwer würde.

Denn ich wollte nicht die Integrationsgrenzen für so einen krummen Körper aufstellen wollen, die sicherstellen, dass nur genau über die Figur laut Aufgabenstellung integriert wird. Denn weder in kartesischen Koordinaten noch in Polarkoordinaten wird das so richtig angenehm.

pingu · Anmeldungsdatum: 30.06.2007 Beiträge: 94

Ok, vielen Dank Thumbs up!

!

Lg
pingu

Gast246 · Gast

Somit setze ich für m1 = (2R)²*pi und für x1=0 ein. Somit fällt m1x1 schon mal weg. Weiter setzte ich für m2 = R²*pi und für x2=-R. Das ergibt für m2x2=-R³*pi. und das schliesslich noch durch m1+m2 teilen. Das ergibt dann .[/quote] Ab diesem Teil steige ich aus, kann mir das evtl. jemand erläutern? Danke im Voraus & liebe Grüße aus Gießen